离群点之所以独特,是因为它们通常不按常理出牌。这些与众不同的数据点可能会扭曲您的分析,并降低预测模型的准确性。尽管检测离群点至关重要,但目前还没有一个普遍认可的方法。虽然一些高级技术(如机器学习)提供了解决方案,但在本章中,您将重点关注数据科学领域中使用了数十年的基础方法。
让我们开始吧。

发现异常:数据科学中离群点检测的经典方法
图片由Haley Truong提供。保留部分权利。
概述
这篇博文分为三部分;它们是:
- 理解离群点及其影响
- 离群点检测的传统方法
- 在Ames数据集中检测离群点
理解离群点及其影响
离群点可能由于各种原因出现,从数据录入错误到真正的异常。它们的存在可归因于以下因素:
- 测量误差
- 数据处理误差
- 真正的极端观测值
了解离群点的来源对于确定是保留、修改还是丢弃它至关重要。离群点对统计分析的影响可能非常深远。它们可以改变数据可视化、集中趋势测量和其他统计测试的结果。离群点还会影响数据集中正态性、线性和同方差性的假设,从而导致不可靠和虚假的结论。
通过我的书籍《数据科学初学者指南》**开启您的项目**。它提供了**带工作代码的自学教程**。
离群点检测的传统方法
在数据科学领域,存在几种检测离群点的经典方法。这些方法大致可分为:
- 可视化方法:散点图、箱线图和直方图等图表提供了数据分布和任何极端值的直观感受。
- 统计方法:Z分数、IQR(四分位距)和修正Z分数等技术是基于数据分布定义离群点的数学方法。
- 概率和统计模型:这些方法利用数据的概率分布(例如高斯分布)来检测不太可能的观测值。
重要的是要理解,方法的选择通常取决于数据集的性质和手头上的具体问题。
在Ames数据集中检测离群点
在本节中,您将深入探讨使用Ames住房数据集检测离群点的实际应用。具体来说,您将探索三个特征:地块面积、销售价格和地上房间总数。
目视检查
视觉方法是识别异常值的快速直观方式。让我们从所选特征的箱线图开始。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 导入必要的库并加载数据集 import pandas as pd import seaborn as sns import matplotlib.pyplot as plt Ames = pd.read_csv('Ames.csv') # 以完整形式定义特征名称,用于标题和坐标轴 feature_names_full = { 'LotArea': '地块面积(平方英尺)', 'SalePrice': '销售价格(美元)', 'TotRmsAbvGrd': '地上房间总数' } plt.figure(figsize=(18, 6)) features = ['LotArea', 'SalePrice', 'TotRmsAbvGrd'] for i, feature in enumerate(features, 1): plt.subplot(1, 3, i) sns.boxplot(y=Ames[feature], color="lightblue") plt.title(feature_names_full[feature], fontsize=16) plt.ylabel(feature_names_full[feature], fontsize=14) plt.xlabel('') # 移除不需要的x轴标签 plt.tight_layout() plt.show() |
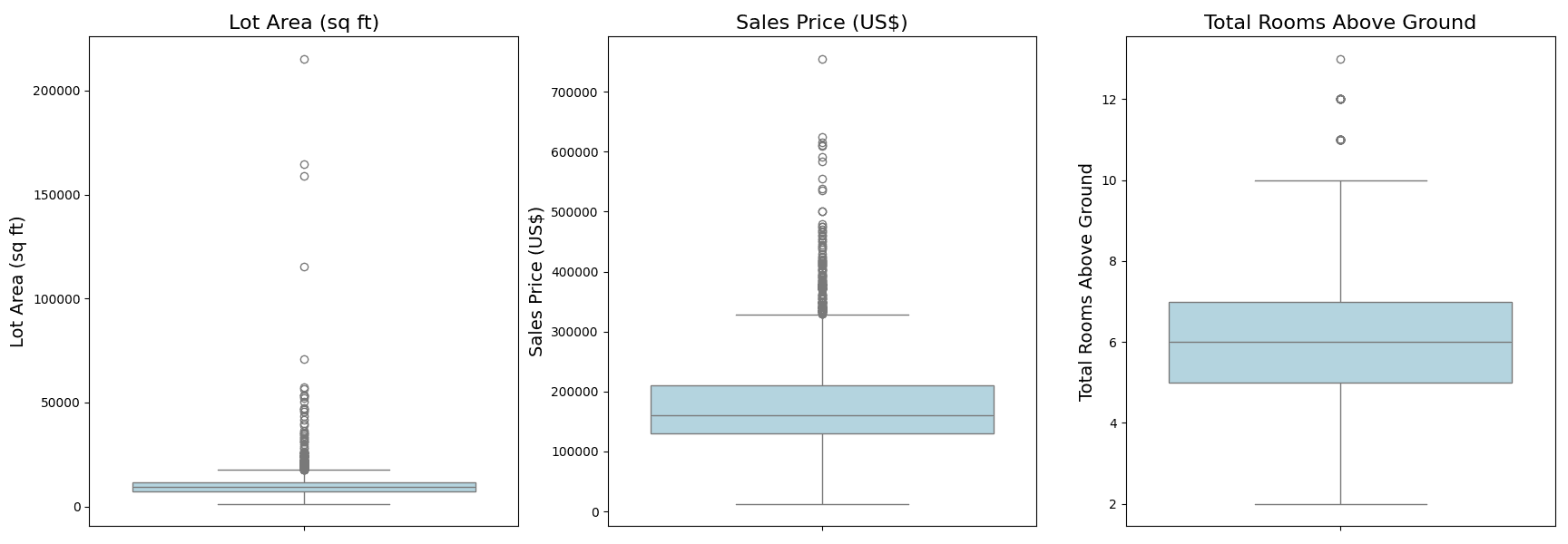
这些图表提供了对数据中潜在离群点的即时洞察。您在“须”之外看到的点代表被认为是离群点的数据点,它们位于第一和第三四分位数(IQR)的1.5倍之外。例如,您可能会注意到地块面积异常大或地上房间数量异常多的房产。
统计方法:IQR
上述箱线图中的点大于第三四分位距(IQR)的1.5倍。这是一种定量识别离群点的稳健方法。您无需箱线图即可从pandas DataFrame中精确地找到并计数这些点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
def detect_outliers_iqr_summary(dataframe, features): outliers_summary = {} for feature in features: data = dataframe[feature] Q1 = data.quantile(0.25) Q3 = data.quantile(0.75) IQR = Q3 - Q1 lower_bound = Q1 - 1.5 * IQR upper_bound = Q3 + 1.5 * IQR outliers = data[(data < lower_bound) | (data > upper_bound)] outliers_summary[feature] = len(outliers) return outliers_summary outliers_summary = detect_outliers_iqr_summary(Ames, features) print(outliers_summary) |
输出如下:
|
1 |
{'LotArea': 113, 'SalePrice': 116, 'TotRmsAbvGrd': 35} |
在您使用四分位距(IQR)方法对Ames住房数据集进行的分析中,您发现“地块面积”特征中有113个离群点,“销售价格”特征中有116个离群点,以及“地上房间总数”特征中有35个离群点。这些离群点在箱线图中被可视化为须线之外的点。箱线图的须线通常延伸到第一和第三四分位距(IQR)的1.5倍之外,超出这些须线的数据点被视为离群点。这只是离群点的一种定义。此类值应在后续分析中进一步调查或适当处理。
概率和统计模型
数据的自然分布有时可以帮助您识别离群点。关于数据分布最常见的假设之一是它遵循高斯(或正态)分布。在一个完美的高斯分布中,大约68%的数据落在距离平均值一个标准差内,95%在两个标准差内,99.7%在三个标准差内。远离平均值的数据点(通常超出三个标准差)可以被认为是离群点。
当数据集很大并且被认为是正态分布时,这种方法特别有效。让我们将这种技术应用于您的Ames住房数据集,看看会发现什么。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# 定义一个使用高斯模型检测离群点的函数 def detect_outliers_gaussian(dataframe, features, threshold=3): outliers_summary = {} for feature in features: data = dataframe[feature] mean = data.mean() std_dev = data.std() outliers = data[(data < mean - threshold * std_dev) | (data > mean + threshold * std_dev)] outliers_summary[feature] = len(outliers) # 可视化 plt.figure(figsize=(12, 6)) sns.histplot(data, color="lightblue") plt.axvline(mean, color='r', linestyle='-', label=f'平均值: {mean:.2f}') plt.axvline(mean - threshold * std_dev, color='y', linestyle='--', label=f'—{threshold} 标准差') plt.axvline(mean + threshold * std_dev, color='g', linestyle='--', label=f'+{threshold} 标准差') # 注释第三个标准差上限值 annotate_text = f'{mean + threshold * std_dev:.2f}' plt.annotate(annotate_text, xy=(mean + threshold * std_dev, 0), xytext=(mean + (threshold + 1.45) * std_dev, 50), arrowprops=dict(facecolor='black', arrowstyle='wedge,tail_width=0.7'), fontsize=12, ha='center') plt.title(f'{feature_names_full[feature]} 的分布及离群点', fontsize=16) plt.xlabel(feature_names_full[feature], fontsize=14) plt.ylabel('频率', fontsize=14) plt.legend() plt.show() return outliers_summary outliers_gaussian_summary = detect_outliers_gaussian(Ames, features) print(outliers_gaussian_summary) |
|
1 |
{'LotArea': 24, 'SalePrice': 42, 'TotRmsAbvGrd': 35} |
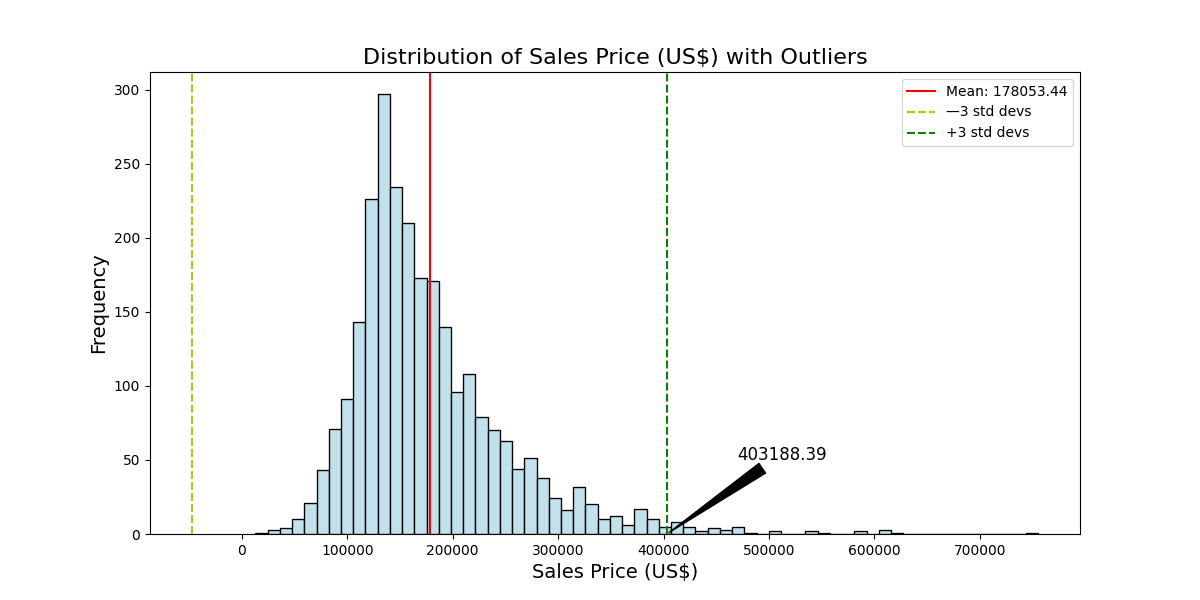
在应用高斯模型进行离群点检测后,您观察到“地块面积”、“销售价格”和“地上房间总数”特征中存在离群点。这些离群点是根据距平均值三个标准差的上限阈值进行识别的。
- 地块面积:任何地块面积大于34,505.44平方英尺的观测值都被视为离群点。您在数据集中发现了24个这样的离群点。
- 销售价格:任何高于403,188.39美元的观测值都被视为离群点。您的分析揭示了“销售价格”特征中有42个离群点。
- 地上房间总数:地上房间数量超过10.99个的观测值被视为离群点。您使用此标准识别了35个离群点。
离群点的数量不同,因为离群点的定义不同。这些数字与您早期的 IQR 方法不同,这强调了使用多种技术以获得更全面理解的重要性。可视化强调了这些离群点,使得它们与数据的主要分布清晰可辨。这种差异强调了在决定离群点管理最佳方法时,领域专业知识和上下文的必要性。
为了增强您的理解并促进进一步分析,编制一份已识别离群点的综合列表是很有价值的。此列表清晰地概述了与常态显著偏离的特定数据点。在下一节中,您将说明如何系统地组织这些离群点,并将其列入每个特征(“地块面积”、“销售价格”和“地上房间总数”)的数据框中。这种表格格式便于检查和采取潜在行动,例如进一步调查或有针对性的数据处理。
让我们探讨完成此任务的方法。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# 定义一个将离群点制成数据框的函数 def create_outliers_dataframes_gaussian(dataframe, features, threshold=3, num_rows=None): outliers_dataframes = {} for feature in features: data = dataframe[feature] mean = data.mean() std_dev = data.std() outliers = data[(data < mean - threshold * std_dev) | (data > mean + threshold * std_dev)] # 为当前特征的离群值创建一个新的数据框 outliers_df = dataframe.loc[outliers.index, [feature]].copy() outliers_df.rename(columns={feature: '离群值'}, inplace=True) outliers_df['特征'] = feature outliers_df.reset_index(inplace=True) # 显示指定行数(默认:完整数据框) outliers_df = outliers_df.head(num_rows) if num_rows is not None else outliers_df outliers_dataframes[feature] = outliers_df return outliers_dataframes # 使用用户定义的行数 = 7 的示例用法 outliers_gaussian_dataframes = create_outliers_dataframes_gaussian(Ames, features, num_rows=7) # 打印每个数据框,使用原始格式和首字母大写的“index” for feature, df in outliers_gaussian_dataframes.items(): df_reset = df.reset_index().rename(columns={'index': '索引'}) print(f"{feature} 的离群值:\n", df_reset[['索引', '特征', '离群值']]) print() |
现在,在揭示结果之前,需要注意的是,这段代码片段允许用户自定义。通过调整参数num_rows,您可以灵活地定义每个数据框中希望看到的行数。在之前分享的示例中,您使用num_rows=7进行了简洁显示,但默认设置为num_rows=None,这将打印整个数据框。请随意根据您的偏好和分析的具体要求来调整此参数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
LotArea 的离群点: 索引 特征 离群值 0 104 LotArea 53107 1 195 LotArea 53227 2 249 LotArea 159000 3 309 LotArea 40094 4 329 LotArea 45600 5 347 LotArea 50271 6 355 LotArea 215245 SalePrice 的离群点: 索引 特征 离群值 0 29 SalePrice 450000 1 65 SalePrice 615000 2 103 SalePrice 468000 3 108 SalePrice 500067 4 124 SalePrice 475000 5 173 SalePrice 423000 6 214 SalePrice 500000 TotRmsAbvGrd 的离群点: 索引 特征 离群值 0 50 TotRmsAbvGrd 12 1 165 TotRmsAbvGrd 11 2 244 TotRmsAbvGrd 11 3 309 TotRmsAbvGrd 11 4 407 TotRmsAbvGrd 11 5 424 TotRmsAbvGrd 13 6 524 TotRmsAbvGrd 11 |
在这次对概率和统计模型进行离群点检测的探索中,您重点关注了应用于Ames住房数据集的高斯模型,特别是使用了三个标准差的阈值。通过利用可视化和统计方法提供的洞察,您识别了离群点并演示了如何在可定制的数据框中列出它们。
想开始学习数据科学新手指南吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
进一步阅读
资源
总结
离群点,源于各种原因,显著影响统计分析。识别它们的来源至关重要,因为它们会扭曲可视化、集中趋势测量和统计测试。数据科学中经典的离群点检测方法包括视觉、统计和概率方法,选择取决于数据集的性质和具体问题。
在Ames住房数据集上应用这些方法,重点关注地块面积、销售价格和地上房间总数,揭示了洞察。箱线图等视觉方法提供了快速的离群点识别。四分位距(IQR)方法量化了离群点,揭示了地块面积、销售价格和地上房间总数分别为113、116和35个离群点。概率模型,特别是具有三个标准差的高斯模型,在相应特征中发现了24、42和35个离群点。
这些结果强调了离群点检测需要多方面的方法。除了识别之外,系统地组织和列表格化的数据框中的离群点有助于深入检查。通过 `num_rows` 参数演示的可定制性确保了在呈现定制结果时的灵活性。总而言之,本次探索增强了对离群点的理解,并为在实际数据集中管理离群点提供了实用指导。
具体来说,你学到了:
- 离群点的重要性及其对数据分析的潜在影响。
- 数据科学中用于离群点检测的各种传统方法。
- 如何将这些方法应用于实际数据集,以Ames住房数据集为例。
- 系统地组织和列出已识别的离群点到可自定义的数据帧中,以进行详细检查和进一步分析。
您有任何问题吗?请在下面的评论中提出您的问题,我将尽力回答。
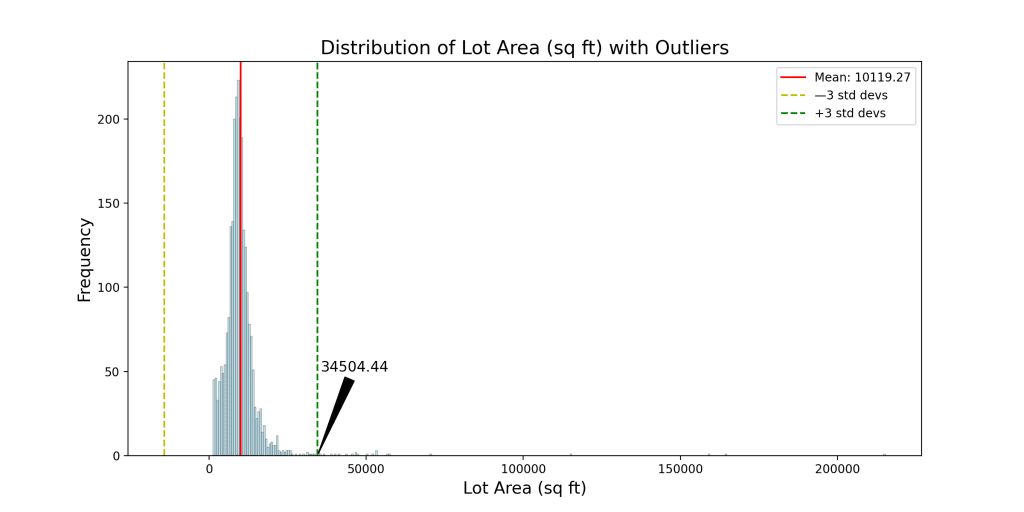
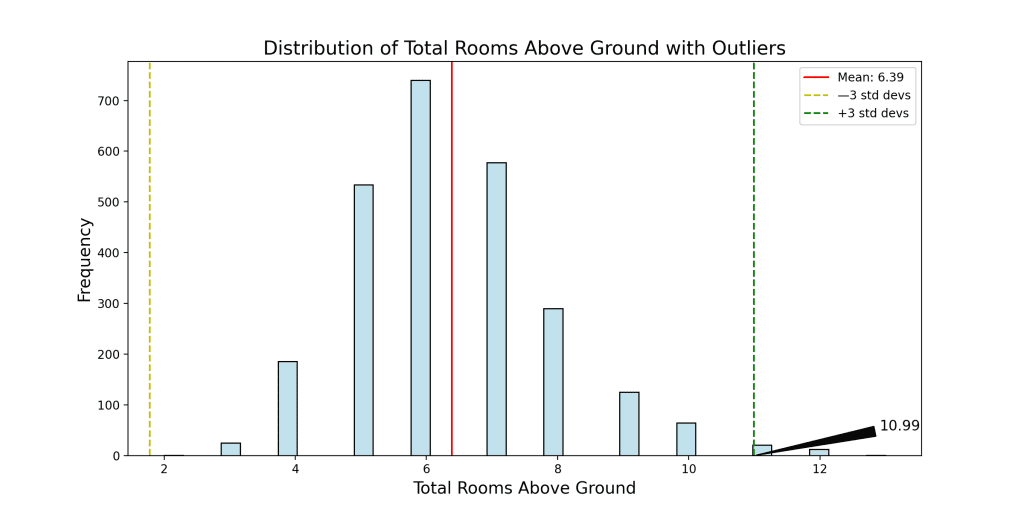





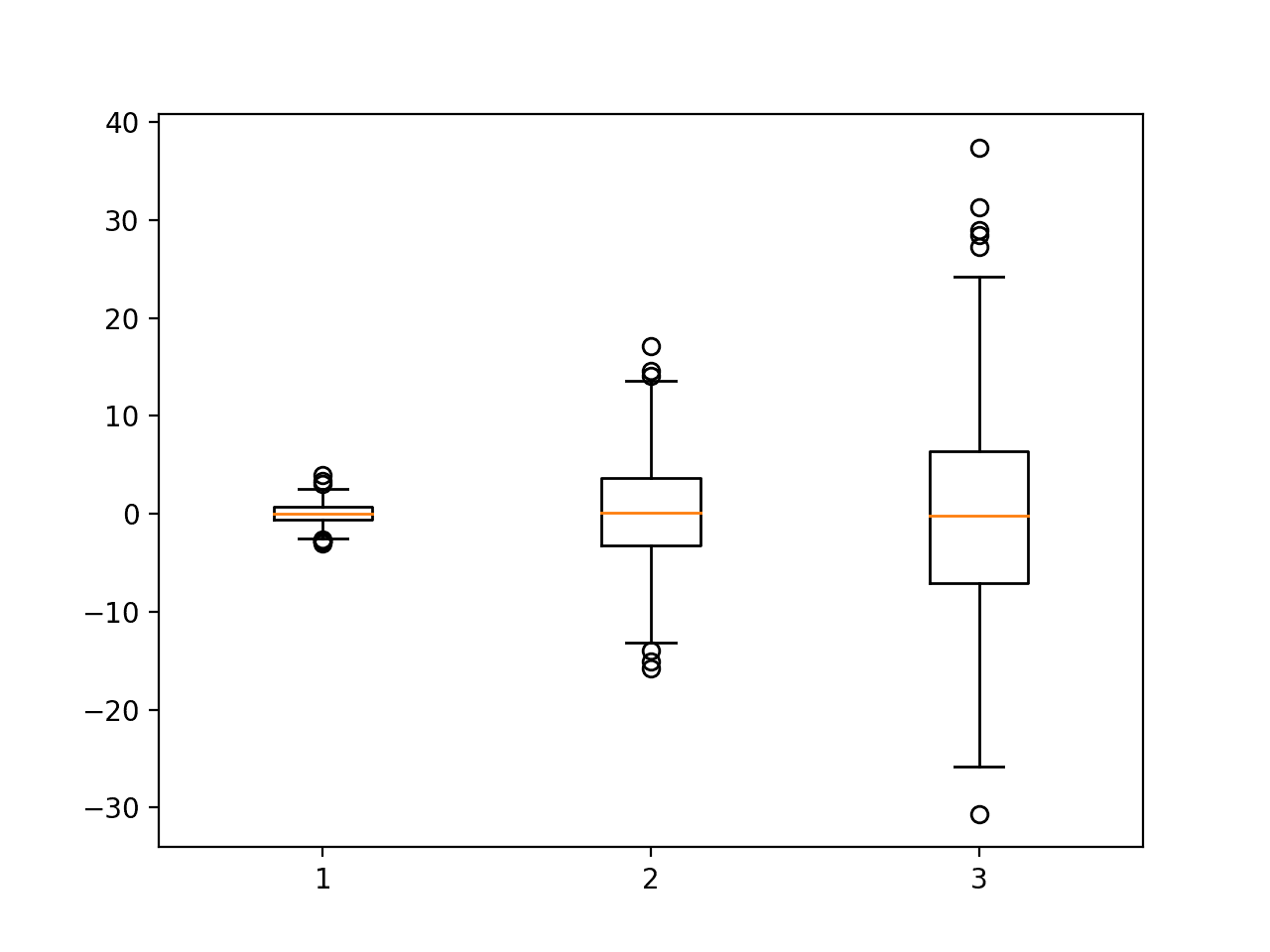

尽管这是一个示例,但住房数据的直方图显然不呈正态分布,值得一提的是,这可能导致数据集中属于分布一部分的数据被排除或突出显示。这在本帖中可以成为一个很好的学习点。
感谢您的反馈和建议!
尊敬的伊恩·亚伯拉罕博士:您在这里提出了一个非常棒的观点。我非常同意您的敏锐观察和建议。在我后续的帖子中,我将讨论如何解决“偏度”问题,其中我将分享各种方法和结果。理想情况下,如果我能将该帖子和这篇帖子结合起来,我们可以提供一个扎实的学习点。如果您能阅读那篇帖子,并让我知道在应用假设高斯分布的标准概率和统计方法检测离群点之前,您会推荐哪种方法来解决偏度,我将不胜感激。您提出的任何其他建议/想法都将非常感谢。我很乐意加强这篇帖子或撰写一篇新的帖子,以妥善解决您的评论。谢谢!
尊敬的Chugani,
非常感谢您与我们分享您的见解!尽管我没有机器学习背景,但您的分析非常清晰,极大地启发了我学习更多关于这个领域的知识。
我强烈推荐年轻的朋友们阅读Chugani的文章和分析。
此致,
萍萍
尊敬的PingPing Wen先生:非常感谢您花时间阅读我的帖子。我很高兴您觉得它们有帮助。我将尽力为您和我们的读者创作更多帖子。我们这里有一个很棒的团队,我得到了Adrian Tam先生(我们的主编)、James Carmichael先生和许多其他人的大力协助。我也会向他们转达您的谢意。
尊敬的Vinod Chugani先生:您撰写的文章信息量极大,非常有帮助。我经常阅读。另外,我想补充一点,一旦识别出异常值,不应总是将其删除。特别是Willia Lakshmanan和Sarah Robinson(如果我名字写错了,提前抱歉)的著作《机器学习:设计模式》中。我建议“不要丢弃异常值”,除非它们是技术错误的结果,因为在这种情况下,如果模型遇到“真正不典型的情况”,将导致难以定义类标签(对于分类任务)!
尊敬的Dmitriy:非常感谢您的评论,以及您对我们博客文章持续的支持和关注。我在这里得到了一个很棒的团队的支持。您提出了一个非常重要的观点。正如上文简要强调的,“理解离群点的来源对于确定是保留、修改还是丢弃它至关重要”。离群点是一种“现实”,最好小心处理它们,因为它们通常具有信息价值,如果我们不仔细检查就将其消除,这些价值就会丢失。我们将继续尽最大努力为您和我们的读者提供有趣的见解。此致,Vinod