用于实践应用机器学习的10个标准数据集

要想在应用机器学习方面有所成就，关键在于练习大量的不同数据集。

这是因为每个问题都不同，需要细微不同的数据准备和建模方法。

在本帖中，您将发现 10 个顶级标准机器学习数据集，可供您练习。

让我们开始吧。

• 更新于 2018 年 3 月：为 Pima Indians 和 Boston Housing 数据集添加了备用下载链接，因为原始链接似乎已被删除。
• 更新于 2019 年 2 月：对保险数据集的预期默认 RMSE 进行了小幅更新。
• 更新于 2021 年 10 月：对小麦种子数据集的描述进行了小幅更新。

概述

结构化方法

每个数据集都以一致的方式进行总结。这使得它们易于比较和导航，以便您练习特定的数据准备技术或建模方法。

您需要了解的关于每个数据集的方面是：

1. 名称：如何引用数据集。
2. 问题类型：问题是回归还是分类。
3. 输入和输出：输入和输出特征的数量和已知名称。
4. 性能：使用零规则算法进行比较的基线性能，以及最佳已知性能（如果已知）。
5. 样本：原始数据的前 5 行快照。
6. 链接：您可以下载数据集并了解更多信息的链接。

标准数据集

下面是我们将在下面介绍的 10 个数据集的列表。

每个数据集都足够小，可以放入内存并在电子表格中进行查看。所有数据集都由表格数据组成，没有（明确的）缺失值。

1. 瑞典汽车保险数据集。
2. 葡萄酒质量数据集。
3. 皮马印第安人糖尿病数据集。
4. 声纳数据集。
5. 钞票数据集。
6. 鸢尾花数据集。
7. 鲍鱼数据集。
8. 电离层数据集。
9. 小麦种子数据集。
10. 波士顿房价数据集。

1. 瑞典汽车保险数据集

瑞典汽车保险数据集涉及根据索赔总数预测所有索赔的总支付金额（以瑞典克朗为单位）。

这是一个回归问题。它包含 63 个观测值，1 个输入变量和 1 个输出变量。变量名称如下：

1. 索赔次数。
2. 所有索赔的总支付金额（以瑞典克朗为单位）。

预测平均值的基线性能是 RMSE 约为 81,000 瑞典克朗。

下面是前 5 行的样本。

下面是整个数据集的散点图。

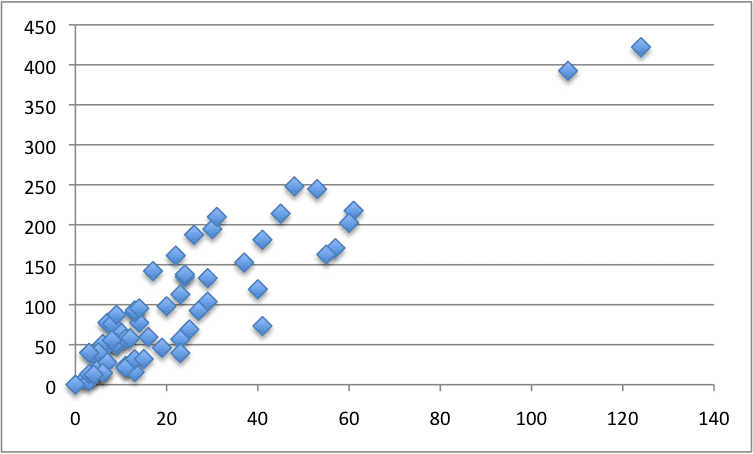
瑞典汽车保险数据集

• 下载
• 更多信息

2. 葡萄酒质量数据集

葡萄酒质量数据集涉及根据每种葡萄酒的化学测量值，按比例预测白葡萄酒的质量。

这是一个多类分类问题，但也可以被视为回归问题。每个类别的观测值数量不平衡。有 4,898 个观测值，11 个输入变量和 1 个输出变量。变量名称如下：

1. 固定酸度。
2. 挥发性酸度。
3. 柠檬酸。
4. 残糖。
5. 氯化物。
6. 游离二氧化硫。
7. 总二氧化硫。
8. 密度。
9. pH 值。
10. 硫酸盐。
11. 酒精。
12. 质量（分数在 0 到 10 之间）。

预测平均值的基线性能是 RMSE 约为 0.148 质量点。

下面是前 5 行的样本。

• 下载
• 更多信息

3. 皮马印第安人糖尿病数据集

皮马印第安人糖尿病数据集涉及根据皮马印第安人的医疗详细信息，预测 5 年内糖尿病的发生。

这是一个二元（2 类）分类问题。每个类别的观测值数量不平衡。有 768 个观测值，8 个输入变量和 1 个输出变量。据信缺失值被编码为零值。变量名称如下：

1. 怀孕次数。
2. 2 小时内口服葡萄糖耐量试验的血浆葡萄糖浓度。
3. 舒张压（mmHg）。
4. 肱三头肌皮褶厚度（mm）。
5. 2 小时血清胰岛素（μU/ml）。
6. 体重指数（体重 kg / 身高 m 的平方）。
7. 糖尿病遗传函数。
8. 年龄（岁）。
9. 类别变量（0 或 1）。

预测最普遍类别的基线性能是分类准确率约为 65%。最高结果的分类准确率约为 77%。

下面是前 5 行的样本。

• 下载
• 更多信息
• 最高结果

4. 声纳数据集

声纳数据集涉及根据不同角度的声纳回波强度来预测物体是水雷还是岩石。

这是一个二元（2 类）分类问题。每个类别的观测值数量不平衡。有 208 个观测值，60 个输入变量和 1 个输出变量。变量名称如下：

1. 不同角度的声纳回波
2. …
3. 类别（M 代表水雷，R 代表岩石）

预测最普遍类别的基线性能是分类准确率约为 53%。最高结果的分类准确率约为 88%。

下面是前 5 行的样本。

• 下载
• 更多信息
• 最高结果

5. 钞票数据集

钞票数据集涉及根据照片上采取的许多测量值来预测给定钞票是否为真。

这是一个二元（2 类）分类问题。每个类别的观测值数量不平衡。有 1,372 个观测值，4 个输入变量和 1 个输出变量。变量名称如下：

1. 小波变换图像的方差（连续）。
2. 小波变换图像的偏度（连续）。
3. 小波变换图像的峰度（连续）。
4. 图像熵（连续）。
5. 类别（0 表示真实，1 表示伪造）。

预测最普遍类别的基线性能是分类准确率约为 50%。

下面是前 5 行的样本。

• 下载
• 更多信息

6. 鸢尾花数据集

鸢尾花数据集涉及根据鸢尾花测量值预测花卉种类。

这是一个多类分类问题。每个类别的观测值数量是平衡的。有 150 个观测值，4 个输入变量和 1 个输出变量。变量名称如下：

1. 花萼长度（厘米）。
2. 花萼宽度（厘米）。
3. 花瓣长度（厘米）。
4. 花瓣宽度（厘米）。
5. 类别（鸢尾花setosa、鸢尾花versicolour、鸢尾花virginica）。

预测最普遍类别的基线性能是分类准确率约为 26%。

下面是前 5 行的样本。

• 下载
• 更多信息

7. 鲍鱼数据集

鲍鱼数据集涉及根据个体物的客观测量值来预测鲍鱼的年龄。

这是一个多类分类问题，但也可以被视为回归问题。每个类别的观测值数量不平衡。有 4,177 个观测值，8 个输入变量和 1 个输出变量。变量名称如下：

1. 性别（M、F、I）。
2. 长度。
3. 直径。
4. 高度。
5. 总重量。
6. 去壳重量。
7. 内脏重量。
8. 壳重。
9. 环数。

预测最普遍类别的基线性能是分类准确率约为 16%。预测平均值的基线性能是 RMSE 约为 3.2 环。

下面是前 5 行的样本。

• 下载
• 更多信息

8. 电离层数据集

电离层数据集要求根据电离层自由电子的雷达回波来预测大气中的结构。

这是一个二元（2 类）分类问题。每个类别的观测值数量不平衡。有 351 个观测值，34 个输入变量和 1 个输出变量。变量名称如下：

1. 17 对雷达回波数据。
2. …
3. 类别（g 代表好，b 代表差）。

预测最普遍类别的基线性能是分类准确率约为 64%。最高结果的分类准确率约为 94%。

下面是前 5 行的样本。

• 下载
• 更多信息
• 最高结果

9. 小麦种子数据集

小麦种子数据集涉及根据不同品种小麦种子的测量值来预测物种。

这是一个多类（3 类）分类问题。每个类别的观测值数量是平衡的。有 210 个观测值，7 个输入变量和 1 个输出变量。变量名称如下：

1. 面积。
2. 周长。
3. 紧凑度
4. 种子长度。
5. 种子宽度。
6. 不对称系数。
7. 种子沟槽长度。
8. 类别（1、2、3）。

预测最普遍类别的基线性能是分类准确率约为 28%。

下面是前 5 行的样本。

• 下载
• 更多信息

10. 波士顿房价数据集

波士顿房价数据集涉及根据房屋及其社区的详细信息预测房屋价格（以千美元为单位）。

这是一个回归问题。有 506 个观测值，13 个输入变量和 1 个输出变量。变量名称如下：

1. CRIM：城镇人均犯罪率。
2. ZN：划定给超过 25,000 平方英尺地块的住宅用地比例。
3. INDUS：城镇非零售商业用地亩数比例。
4. CHAS：查尔斯河虚拟变量（= 1 如果地块临河；否则为 0）。
5. NOX：一氧化氮浓度（百万分之十）。
6. RM：每户平均房间数。
7. AGE：1940 年前建造的自住单元比例。
8. DIS：到五个波士顿就业中心的加权距离。
9. RAD：通往辐射状高速公路的可达性指数。
10. TAX：每 10,000 美元的全部财产税率。
11. PTRATIO：城镇师生比例。
12. B：1000(Bk – 0.63)^2，其中 Bk 是城镇黑人比例。
13. LSTAT：人口中的低收入者百分比。
14. MEDV：自住房屋的中位数价值（以千美元计）。

预测平均值的基线性能是 RMSE 约为 9.21 千美元。

下面是前 5 行的样本。

• 下载（更新：从这里下载）
• 更多信息

总结

在本帖中，您了解了 10 个顶级标准数据集，可用于练习应用机器学习。

您的下一步是：

1. 选择一个数据集。
2. 使用您喜欢的工具（如 Weka、scikit-learn 或 R）
3. 看看您能将标准分数提高多少。
4. 在下面的评论中报告您的结果。