如何在 Python 中使用 StandardScaler 和 MinMaxScaler 转换

作者： Jason Brownlee 发布于 2020 年 8 月 28 日在数据准备 81 条评论

当数值输入变量被缩放到标准范围时，许多机器学习算法表现更好。

这包括使用输入加权和的算法，如线性回归，以及使用距离度量的算法，如 k 近邻。

在建模之前缩放数值数据的两种最流行技术是归一化和标准化。**归一化**将每个输入变量单独缩放到 0-1 的范围，这是我们精度最高的浮点值范围。**标准化**通过减去均值（称为居中）并除以标准差来单独缩放每个输入变量，以使分布具有零均值和一标准差。

在本教程中，您将学习如何使用缩放器转换来标准化和归一化分类和回归的数值输入变量。

完成本教程后，您将了解：

数据缩放是使用许多机器学习算法时推荐的预处理步骤。
数据缩放可以通过归一化或标准化实值输入和输出变量来实现。
如何应用标准化和归一化来提高预测建模算法的性能。

使用我的新书《机器学习数据准备》**启动您的项目**，其中包括**分步教程**和所有示例的 **Python 源代码**文件。

让我们开始吧。

How to Use StandardScaler and MinMaxScaler Transforms

如何使用 StandardScaler 和 MinMaxScaler 转换
照片由 Marco Verch 拍摄，保留部分权利。

教程概述

本教程分为六个部分；它们是：

数据规模的重要性
数值数据缩放方法
1. 数据归一化
2. 数据标准化
声纳数据集
MinMaxScaler 转换
StandardScaler 转换
常见问题

数据规模的重要性

机器学习模型学习从输入变量到输出变量的映射。

因此，从域中提取的数据的比例和分布对于每个变量可能不同。

输入变量可能具有不同的单位（例如英尺、公里和小时），这反过来可能意味着变量具有不同的尺度。

输入变量之间尺度的差异可能会增加建模问题的难度。一个例子是，大的输入值（例如，数百或数千个单位的范围）可能导致模型学习大的权重值。具有大权重值的模型通常不稳定，这意味着它在学习过程中可能会表现不佳，并且对输入值敏感，从而导致更高的泛化误差。

最常见的预处理形式之一是对输入变量进行简单的线性重新缩放。

— 第 298 页，《模式识别神经网络》，1995 年。

输入变量尺度上的这种差异并不影响所有机器学习算法。

例如，使用输入变量加权和来拟合模型的算法会受到影响，例如线性回归、逻辑回归和人工神经网络（深度学习）。

例如，当使用预测变量之间的距离或点积（如 K 近邻或支持向量机）或当变量需要共同尺度才能应用惩罚时，标准化过程至关重要。

— 第 124 页，《特征工程与选择》，2019 年。

此外，使用示例或原型之间距离度量的算法也会受到影响，例如 k 近邻和支持向量机。也有一些算法不受数值输入变量尺度影响，最显著的是决策树和树的集成，如随机森林。

不同的属性以不同的尺度测量，因此如果直接使用欧几里德距离公式，一些属性的影响可能会被那些具有更大测量尺度的属性完全淹没。因此，通常会对所有属性值进行归一化……

— 第 145 页，《数据挖掘：实用机器学习工具和技术》，2016 年。

对于回归预测建模问题，缩放目标变量以使问题更容易学习也是一个好主意，尤其是在神经网络模型的情况下。具有大值范围的目标变量反过来可能导致大的误差梯度值，导致权重值发生剧烈变化，使学习过程不稳定。

缩放输入和输出变量是使用神经网络模型的关键步骤。

在实践中，在将输入数据呈现给网络之前对其进行预处理转换几乎总是有利的。同样，网络的输出通常会进行后处理以给出所需的输出值。

— 第 296 页，《模式识别神经网络》，1995 年。

想开始学习数据准备吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

数值数据缩放方法

归一化和标准化都可以使用 scikit-learn 库实现。

让我们依次仔细看看每一个。

数据归一化

归一化是将数据从原始范围重新缩放到所有值都在 0 到 1 的新范围内。

归一化要求您知道或能够准确估计最小和最大可观测值。您可以从可用数据中估计这些值。

属性通常通过将所有值除以遇到的最大值或通过减去最小值并除以最大值和最小值之间的范围来归一化到固定范围——通常从零到一。

— 第 61 页，《数据挖掘：实用机器学习工具和技术》，2016 年。

值归一化如下

y = (x – min) / (max – min)

其中最小值和最大值与正在归一化的值 x 相关。

例如，对于一个数据集，我们可以猜测最小和最大可观测值为 30 和 -10。然后我们可以归一化任何值，如 18.8，如下所示

y = (x – min) / (max – min)
y = (18.8 – (-10)) / (30 – (-10))
y = 28.8 / 40
y = 0.72

您可以看到，如果提供的值 x 超出最小和最大值的范围，则结果值将不在 0 到 1 的范围内。您可以在进行预测之前检查这些观测值，并将其从数据集中删除或将其限制为预定义的最小或最大值。

您可以使用 scikit-learn 对象 MinMaxScaler 来归一化您的数据集。

MinMaxScaler 和其他缩放技术的良好实践用法如下

**使用可用的训练数据拟合缩放器**。对于归一化，这意味着训练数据将用于估计最小和最大可观测值。这是通过调用 `fit()` 函数完成的。
**将尺度应用于训练数据**。这意味着您可以使用归一化数据来训练您的模型。这是通过调用 `transform()` 函数完成的。
**将尺度应用于未来的数据**。这意味着您可以在未来准备新数据，您想对其进行预测。

`MinMaxScaler` 的默认尺度是将变量重新缩放到 [0,1] 范围，尽管可以通过“`feature_range`”参数指定首选尺度并指定一个元组，包括所有变量的最小值和最大值。

我们可以通过将两个变量转换为 0 到 1 的范围（归一化的默认范围）来演示此类的用法。第一个变量的值介于 4 到 100 之间，第二个变量的值介于 0.1 到 0.001 之间。

完整的示例如下所示。

# example of a normalization
from numpy import asarray
from sklearn.preprocessing import MinMaxScaler
# define data
data = asarray([[100, 0.001],
				[8, 0.05],
				[50, 0.005],
				[88, 0.07],
				[4, 0.1]])
print(data)
# define min max scaler
scaler = MinMaxScaler()
# transform data
scaled = scaler.fit_transform(data)
print(scaled)

# 归一化示例

from numpy import asarray

from sklearn.preprocessing import MinMaxScaler

# 定义数据

data = asarray([[100, 0.001],

[8, 0.05],

[50, 0.005],

[88, 0.07],

[4, 0.1]])

print(data)

# 定义 min max 缩放器

scaler = MinMaxScaler()

# 转换数据

scaled = scaler.fit_transform(data)

print(scaled)

运行示例首先报告原始数据集，显示 2 列 4 行。这些值以科学计数法表示，如果您不习惯，可能难以阅读。

接下来，定义缩放器，在整个数据集上拟合，然后用于创建数据集的转换版本，其中每列独立归一化。我们可以看到每列的最大原始值现在为 1.0，每列的最小值现在为 0.0。

[[1.0e+02 1.0e-03]
 [8.0e+00 5.0e-02]
 [5.0e+01 5.0e-03]
 [8.8e+01 7.0e-02]
 [4.0e+00 1.0e-01]]
[[1.         0.        ]
 [0.04166667 0.49494949]
 [0.47916667 0.04040404]
 [0.875      0.6969697 ]
 [0.         1.        ]]

[[1.0e+02 1.0e-03]

[8.0e+00 5.0e-02]

[5.0e+01 5.0e-03]

[8.8e+01 7.0e-02]

[4.0e+00 1.0e-01]]

[[1. 0. ]

[0.04166667 0.49494949]

[0.47916667 0.04040404]

[0.875 0.6969697 ]

[0. 1. ]]

现在我们熟悉了归一化，让我们仔细看看标准化。

数据标准化

标准化数据集涉及重新缩放值的分布，使观测值的平均值为 0，标准差为 1。

这可以看作是减去平均值或居中数据。

与归一化一样，当您的数据具有不同尺度的输入值时，标准化在某些机器学习算法中可能很有用，甚至必不可少。

标准化假定您的观测值符合高斯分布（钟形曲线），并具有良好的均值和标准差。如果未满足此预期，您仍然可以标准化数据，但可能无法获得可靠的结果。

另一种 [...] 技术是计算属性值的统计平均值和标准差，从每个值中减去平均值，然后将结果除以标准差。这个过程称为统计变量标准化，它产生一组平均值为零且标准差为一的值。

— 第 61 页，《数据挖掘：实用机器学习工具和技术》，2016 年。

标准化要求您知道或能够准确估计可观测值的均值和标准差。您可以从训练数据（而不是整个数据集）中估计这些值。

再次强调，转换所需的统计量（例如，均值）是从训练集中估计的，并应用于所有数据集（例如，测试集或新样本）。

— 第 124 页，《特征工程与选择》，2019 年。

从数据中减去均值称为**居中**，而除以标准差称为**缩放**。因此，该方法有时称为“**中心缩放**”。

最直接和常见的数据转换是中心缩放预测变量。要居中预测变量，从所有值中减去平均预测值。居中后，预测变量的均值为零。同样，为了缩放数据，预测变量的每个值都除以其标准差。缩放数据会强制值具有共同的标准差为一。

— 第 30 页，《应用预测建模》，2013 年。

值标准化如下

y = (x – mean) / standard_deviation

其中 `mean` 计算如下

mean = sum(x) / count(x)

并且 `standard_deviation` 计算如下

standard_deviation = sqrt( sum( (x – mean)^2 ) / count(x))

我们可以估计均值为 10.0，标准差约为 5.0。使用这些值，我们可以标准化第一个值 20.7，如下所示

y = (x – mean) / standard_deviation
y = (20.7 – 10) / 5
y = (10.7) / 5
y = 2.14

数据集的均值和标准差估计比最小值和最大值对新数据更稳健。

您可以使用 scikit-learn 对象 StandardScaler 来标准化您的数据集。

我们可以通过将两个变量转换为上一节中定义的 0 到 1 的范围来演示此类的用法。我们将使用默认配置，该配置将同时居中和缩放每列中的值，例如完全标准化。

完整的示例如下所示。

# example of a standardization
from numpy import asarray
from sklearn.preprocessing import StandardScaler
# define data
data = asarray([[100, 0.001],
				[8, 0.05],
				[50, 0.005],
				[88, 0.07],
				[4, 0.1]])
print(data)
# define standard scaler
scaler = StandardScaler()
# transform data
scaled = scaler.fit_transform(data)
print(scaled)

# 标准化示例

from numpy import asarray

from sklearn.preprocessing import StandardScaler

# 定义数据

data = asarray([[100, 0.001],

[8, 0.05],

[50, 0.005],

[88, 0.07],

[4, 0.1]])

print(data)

# 定义标准缩放器

scaler = StandardScaler()

# 转换数据

scaled = scaler.fit_transform(data)

print(scaled)

运行示例首先报告原始数据集，显示 2 列 4 行，与之前相同。

接下来，定义缩放器，在整个数据集上拟合，然后用于创建数据集的转换版本，其中每列独立标准化。我们可以看到每列中的平均值（如果存在）被赋为 0.0，并且值围绕 0.0 居中，既有正值也有负值。

[[1.0e+02 1.0e-03]
 [8.0e+00 5.0e-02]
 [5.0e+01 5.0e-03]
 [8.8e+01 7.0e-02]
 [4.0e+00 1.0e-01]]
[[ 1.26398112 -1.16389967]
 [-1.06174414  0.12639634]
 [ 0.         -1.05856939]
 [ 0.96062565  0.65304778]
 [-1.16286263  1.44302493]]

[[1.0e+02 1.0e-03]

[8.0e+00 5.0e-02]

[5.0e+01 5.0e-03]

[8.8e+01 7.0e-02]

[4.0e+00 1.0e-01]]

[[ 1.26398112 -1.16389967]

[-1.06174414 0.12639634]

[ 0. -1.05856939]

[ 0.96062565 0.65304778]

[-1.16286263 1.44302493]]

接下来，我们可以介绍一个真实数据集，它为将归一化和标准化转换作为建模的一部分应用提供了基础。

声纳数据集

声纳数据集是用于二元分类的标准机器学习数据集。

它涉及 60 个实值输入和一个二类目标变量。数据集中有 208 个示例，并且类别相当平衡。

基线分类算法使用重复分层 10 折交叉验证可实现约 53.4% 的分类精度。该数据集的最高性能使用重复分层 10 折交叉验证约为 88%。

数据集描述了岩石或模拟地雷的雷达回波。

您可以从这里了解更多关于数据集的信息

无需下载数据集；我们将从我们的示例中自动下载它。

首先，让我们加载并总结数据集。完整的示例列在下面。

# load and summarize the sonar dataset
from pandas import read_csv
from pandas.plotting import scatter_matrix
from matplotlib import pyplot
# Load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"
dataset = read_csv(url, header=None)
# summarize the shape of the dataset
print(dataset.shape)
# summarize each variable
print(dataset.describe())
# histograms of the variables
dataset.hist()
pyplot.show()

# 加载并总结声纳数据集

from pandas import read_csv

from pandas.plotting import scatter_matrix

from matplotlib import pyplot

# 加载数据集

url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"

dataset = read_csv(url, header=None)

# 总结数据集的形状

print(dataset.shape)

# 总结每个变量

print(dataset.describe())

# 变量的直方图

dataset.hist()

pyplot.show()

运行示例首先总结加载数据集的形状。

这证实了 60 个输入变量、一个输出变量和 208 行数据。

提供了输入变量的统计摘要，显示值是数值，大约在 0 到 1 之间。

(208, 61)
               0           1           2   ...          57          58          59
count  208.000000  208.000000  208.000000  ...  208.000000  208.000000  208.000000
mean     0.029164    0.038437    0.043832  ...    0.007949    0.007941    0.006507
std      0.022991    0.032960    0.038428  ...    0.006470    0.006181    0.005031
min      0.001500    0.000600    0.001500  ...    0.000300    0.000100    0.000600
25%      0.013350    0.016450    0.018950  ...    0.003600    0.003675    0.003100
50%      0.022800    0.030800    0.034300  ...    0.005800    0.006400    0.005300
75%      0.035550    0.047950    0.057950  ...    0.010350    0.010325    0.008525
max      0.137100    0.233900    0.305900  ...    0.044000    0.036400    0.043900

[8 rows x 60 columns]

(208, 61)

0 1 2 ... 57 58 59

count 208.000000 208.000000 208.000000 ... 208.000000 208.000000 208.000000

mean 0.029164 0.038437 0.043832 ... 0.007949 0.007941 0.006507

std 0.022991 0.032960 0.038428 ... 0.006470 0.006181 0.005031

min 0.001500 0.000600 0.001500 ... 0.000300 0.000100 0.000600

25% 0.013350 0.016450 0.018950 ... 0.003600 0.003675 0.003100

50% 0.022800 0.030800 0.034300 ... 0.005800 0.006400 0.005300

75% 0.035550 0.047950 0.057950 ... 0.010350 0.010325 0.008525

max 0.137100 0.233900 0.305900 ... 0.044000 0.036400 0.043900

[8 rows x 60 columns]

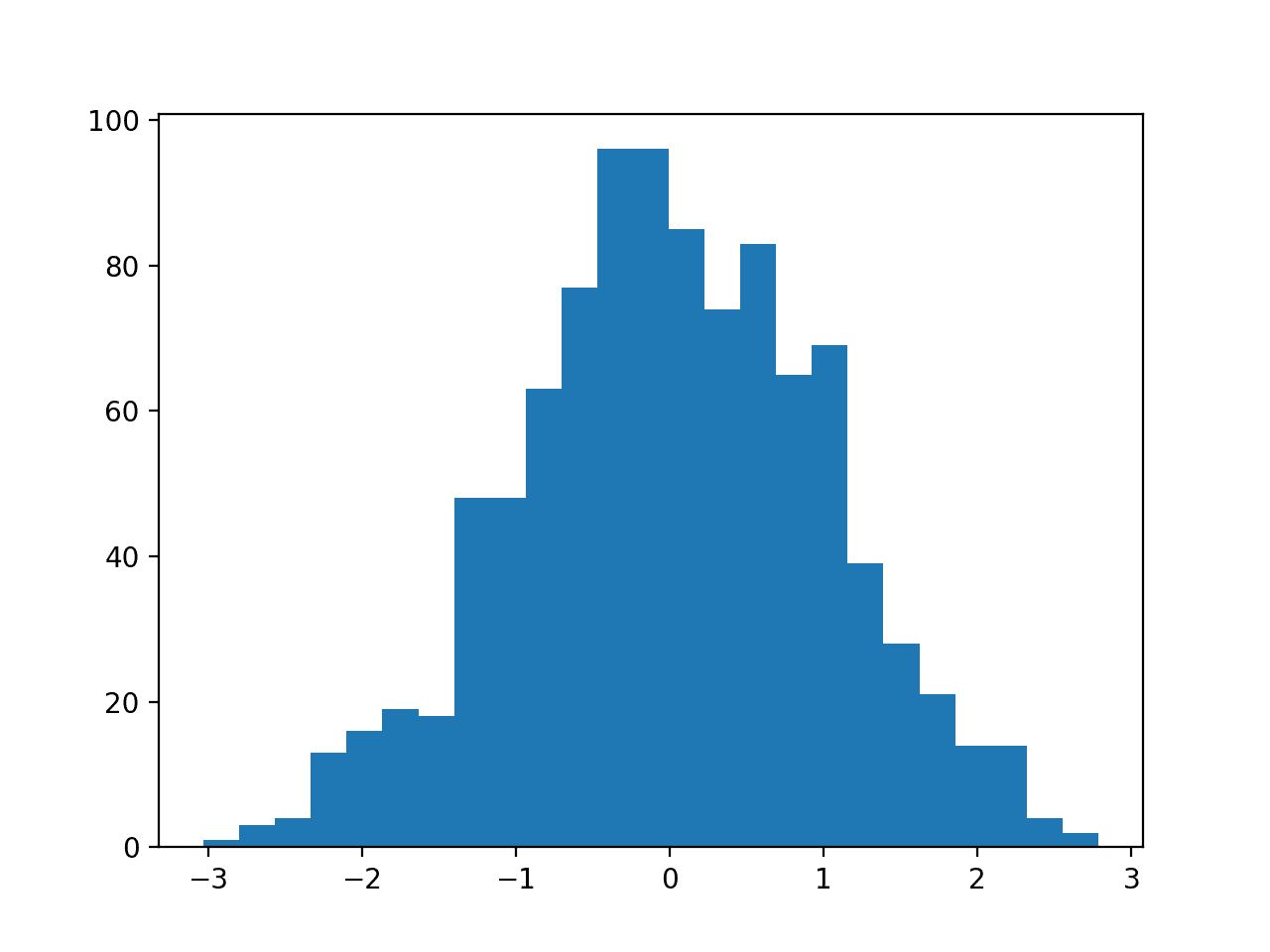
最后，为每个输入变量创建了一个直方图。

如果我们忽略图表的杂乱，只关注直方图本身，我们可以看到许多变量具有偏斜分布。

该数据集为使用缩放器转换提供了很好的候选，因为变量具有不同的最小值和最大值，以及不同的数据分布。

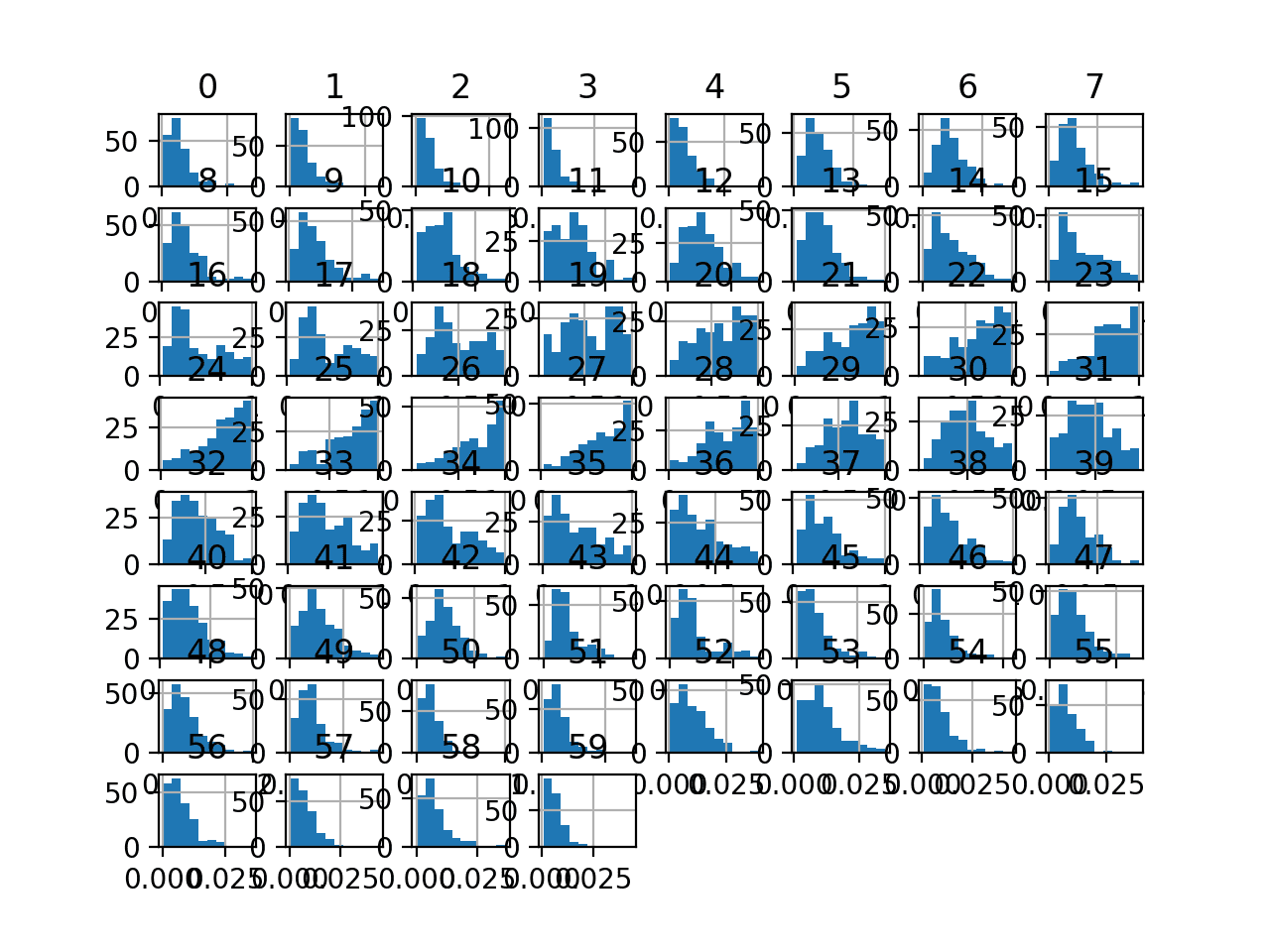
Histogram Plots of Input Variables for the Sonar Binary Classification Dataset

声纳二元分类数据集输入变量的直方图图

接下来，让我们在原始数据集上拟合和评估一个机器学习模型。

我们将使用默认超参数的 k 近邻算法，并使用重复分层 k 折交叉验证对其进行评估。完整示例如下所示。

# evaluate knn on the raw sonar dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from matplotlib import pyplot
# load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"
dataset = read_csv(url, header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define and configure the model
model = KNeighborsClassifier()
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report model performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

# 在原始声纳数据集上评估 knn

from numpy import mean

from numpy import std

from pandas import read_csv

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.neighbors import KNeighborsClassifier

from sklearn.preprocessing import LabelEncoder

from matplotlib import pyplot

# 加载数据集

url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"

dataset = read_csv(url, header=None)

data = dataset.values

# 分割为输入和输出列

X, y = data[:, :-1], data[:, -1]

# 确保输入是浮点数，输出是整数标签

X = X.astype('float32')

y = LabelEncoder().fit_transform(y.astype('str'))

# 定义和配置模型

model = KNeighborsClassifier()

# 评估模型

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')

# 报告模型性能

print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行示例评估 KNN 模型在原始声纳数据集上的性能。

**注意**：由于算法或评估过程的随机性，或者数值精度差异，您的结果可能会有所不同。考虑运行示例几次并比较平均结果。

我们可以看到，该模型实现了大约 79.7% 的平均分类准确率，这表明它具有技能（优于 53.4%），并且接近良好性能（88%）。

Accuracy: 0.797 (0.073)

1	准确率：0.797 (0.073)

接下来，让我们探索数据集的缩放转换。

MinMaxScaler 转换

我们可以将 `MinMaxScaler` 直接应用于 Sonar 数据集以归一化输入变量。

我们将使用默认配置并将值缩放到 0 到 1 的范围。首先，定义一个具有默认超参数的 `MinMaxScaler` 实例。定义后，我们可以调用 `fit_transform()` 函数并将其传递给我们的数据集，以创建数据集的转换版本。

...
# perform a robust scaler transform of the dataset
trans = MinMaxScaler()
data = trans.fit_transform(data)

...

# 对数据集执行稳健缩放器转换

trans = MinMaxScaler()

data = trans.fit_transform(data)

让我们在声纳数据集上尝试一下。

创建声纳数据集的 `MinMaxScaler` 转换并绘制结果直方图的完整示例如下所示。

# visualize a minmax scaler transform of the sonar dataset
from pandas import read_csv
from pandas import DataFrame
from pandas.plotting import scatter_matrix
from sklearn.preprocessing import MinMaxScaler
from matplotlib import pyplot
# load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"
dataset = read_csv(url, header=None)
# retrieve just the numeric input values
data = dataset.values[:, :-1]
# perform a robust scaler transform of the dataset
trans = MinMaxScaler()
data = trans.fit_transform(data)
# convert the array back to a dataframe
dataset = DataFrame(data)
# summarize
print(dataset.describe())
# histograms of the variables
dataset.hist()
pyplot.show()

# 可视化声纳数据集的 minmax 缩放器转换

from pandas import read_csv

from pandas import DataFrame

from pandas.plotting import scatter_matrix

从 sklearn.预处理导入 MinMaxScaler

from matplotlib import pyplot

# 加载数据集

url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"

dataset = read_csv(url, header=None)

# 仅检索数字输入值

data = dataset.values[:, :-1]

# 对数据集执行稳健缩放器转换

trans = MinMaxScaler()

data = trans.fit_transform(data)

# 将数组转换回数据框

dataset = DataFrame(data)

# 总结

print(dataset.describe())

# 变量的直方图

dataset.hist()

pyplot.show()

运行示例首先报告每个输入变量的摘要。

我们可以看到分布已经调整，并且每个变量的最小值和最大值现在分别为清晰的 0.0 和 1.0。

               0           1           2   ...          57          58          59
count  208.000000  208.000000  208.000000  ...  208.000000  208.000000  208.000000
mean     0.204011    0.162180    0.139068  ...    0.175035    0.216015    0.136425
std      0.169550    0.141277    0.126242  ...    0.148051    0.170286    0.116190
min      0.000000    0.000000    0.000000  ...    0.000000    0.000000    0.000000
25%      0.087389    0.067938    0.057326  ...    0.075515    0.098485    0.057737
50%      0.157080    0.129447    0.107753  ...    0.125858    0.173554    0.108545
75%      0.251106    0.202958    0.185447  ...    0.229977    0.281680    0.183025
max      1.000000    1.000000    1.000000  ...    1.000000    1.000000    1.000000

[8 rows x 60 columns]

0 1 2 ... 57 58 59

count 208.000000 208.000000 208.000000 ... 208.000000 208.000000 208.000000

mean 0.204011 0.162180 0.139068 ... 0.175035 0.216015 0.136425

std 0.169550 0.141277 0.126242 ... 0.148051 0.170286 0.116190

min 0.000000 0.000000 0.000000 ... 0.000000 0.000000 0.000000

25% 0.087389 0.067938 0.057326 ... 0.075515 0.098485 0.057737

50% 0.157080 0.129447 0.107753 ... 0.125858 0.173554 0.108545

75% 0.251106 0.202958 0.185447 ... 0.229977 0.281680 0.183025

max 1.000000 1.000000 1.000000 ... 1.000000 1.000000 1.000000

[8 rows x 60 columns]

变量的直方图已创建，但分布看起来与上一节中看到的原始分布没有太大差异。

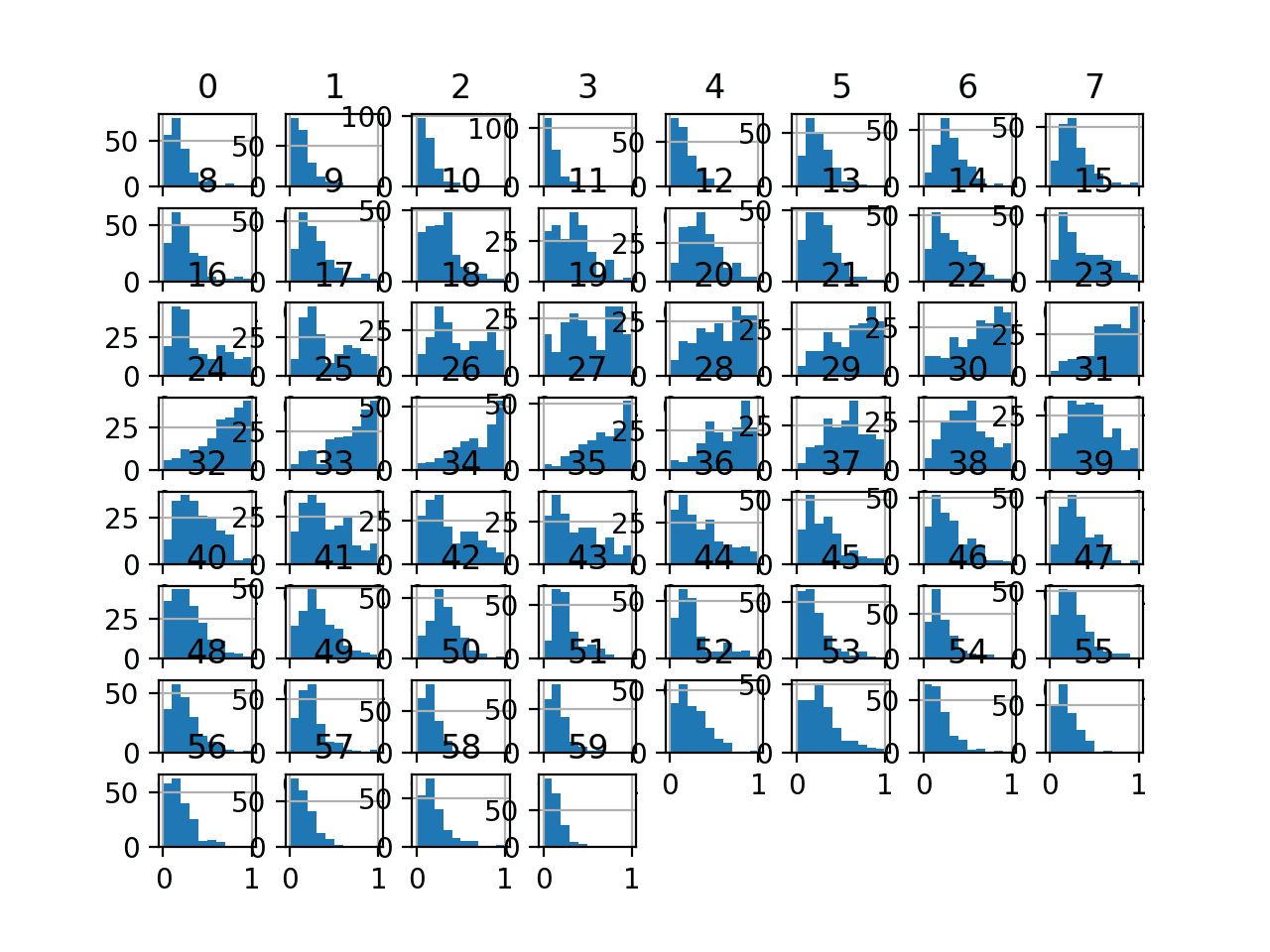
Histogram Plots of MinMaxScaler Transformed Input Variables for the Sonar Dataset

声纳数据集的 MinMaxScaler 转换输入变量直方图

接下来，让我们评估与上一节相同的 KNN 模型，但在此情况下，是在数据集的 `MinMaxScaler` 转换上。

完整的示例如下所示。

# evaluate knn on the sonar dataset with minmax scaler transform
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline
from matplotlib import pyplot
# load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"
dataset = read_csv(url, header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define the pipeline
trans = MinMaxScaler()
model = KNeighborsClassifier()
pipeline = Pipeline(steps=[('t', trans), ('m', model)])
# evaluate the pipeline
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report pipeline performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

# 使用 minmax 缩放器转换在声纳数据集上评估 knn

from numpy import mean

from numpy import std

from pandas import read_csv

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.neighbors import KNeighborsClassifier

from sklearn.preprocessing import LabelEncoder

从 sklearn.预处理导入 MinMaxScaler

from sklearn.pipeline import Pipeline

from matplotlib import pyplot

# 加载数据集

url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"

dataset = read_csv(url, header=None)

data = dataset.values

# 分割为输入和输出列

X, y = data[:, :-1], data[:, -1]

# 确保输入是浮点数，输出是整数标签

X = X.astype('float32')

y = LabelEncoder().fit_transform(y.astype('str'))

# 定义管道

trans = MinMaxScaler()

model = KNeighborsClassifier()

pipeline = Pipeline(steps=[('t', trans), ('m', model)])

# 评估管道

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')

# 报告管道性能

print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

**注意**：由于算法或评估过程的随机性，或者数值精度差异，您的结果可能会有所不同。考虑运行示例几次并比较平均结果。

运行示例，我们可以看到 `MinMaxScaler` 转换使性能提升，从没有转换的 79.7% 准确率提高到有转换的约 81.3%。

Accuracy: 0.813 (0.085)

1	准确率：0.813 (0.085)

接下来，让我们探讨标准化输入变量的效果。

StandardScaler 转换

我们可以将 `StandardScaler` 直接应用于 Sonar 数据集以标准化输入变量。

我们将使用默认配置并将值缩放，以减去均值使其居中于 0.0，并除以标准差以使标准差为 1.0。首先，定义一个具有默认超参数的 `StandardScaler` 实例。

定义后，我们可以调用 `fit_transform()` 函数并将其传递给我们的数据集，以创建数据集的转换版本。

...
# perform a robust scaler transform of the dataset
trans = StandardScaler()
data = trans.fit_transform(data)

...

# 对数据集执行稳健缩放器转换

trans = StandardScaler()

data = trans.fit_transform(data)

让我们在声纳数据集上尝试一下。

创建声纳数据集的 `StandardScaler` 转换并绘制结果直方图的完整示例如下所示。

# visualize a standard scaler transform of the sonar dataset
from pandas import read_csv
from pandas import DataFrame
from pandas.plotting import scatter_matrix
from sklearn.preprocessing import StandardScaler
from matplotlib import pyplot
# load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"
dataset = read_csv(url, header=None)
# retrieve just the numeric input values
data = dataset.values[:, :-1]
# perform a robust scaler transform of the dataset
trans = StandardScaler()
data = trans.fit_transform(data)
# convert the array back to a dataframe
dataset = DataFrame(data)
# summarize
print(dataset.describe())
# histograms of the variables
dataset.hist()
pyplot.show()

# 可视化声纳数据集的标准缩放器转换

from pandas import read_csv

from pandas import DataFrame

from pandas.plotting import scatter_matrix

from sklearn.preprocessing import StandardScaler

from matplotlib import pyplot

# 加载数据集

url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"

dataset = read_csv(url, header=None)

# 仅检索数字输入值

data = dataset.values[:, :-1]

# 对数据集执行稳健缩放器转换

trans = StandardScaler()

data = trans.fit_transform(data)

# 将数组转换回数据框

dataset = DataFrame(data)

# 总结

print(dataset.describe())

# 变量的直方图

dataset.hist()

pyplot.show()

运行示例首先报告每个输入变量的摘要。

我们可以看到分布已经调整，并且每个变量的均值是一个非常接近零的小数，标准差非常接近 1.0。

                 0             1   ...            58            59
count  2.080000e+02  2.080000e+02  ...  2.080000e+02  2.080000e+02
mean  -4.190024e-17  1.663333e-16  ...  1.283695e-16  3.149190e-17
std    1.002413e+00  1.002413e+00  ...  1.002413e+00  1.002413e+00
min   -1.206158e+00 -1.150725e+00  ... -1.271603e+00 -1.176985e+00
25%   -6.894939e-01 -6.686781e-01  ... -6.918580e-01 -6.788714e-01
50%   -2.774703e-01 -2.322506e-01  ... -2.499546e-01 -2.405314e-01
75%    2.784345e-01  2.893335e-01  ...  3.865486e-01  4.020352e-01
max    4.706053e+00  5.944643e+00  ...  4.615037e+00  7.450343e+00

[8 rows x 60 columns]

0 1 ... 58 59

count 2.080000e+02 2.080000e+02 ... 2.080000e+02 2.080000e+02

mean -4.190024e-17 1.663333e-16 ... 1.283695e-16 3.149190e-17

std 1.002413e+00 1.002413e+00 ... 1.002413e+00 1.002413e+00

min -1.206158e+00 -1.150725e+00 ... -1.271603e+00 -1.176985e+00

25% -6.894939e-01 -6.686781e-01 ... -6.918580e-01 -6.788714e-01

50% -2.774703e-01 -2.322506e-01 ... -2.499546e-01 -2.285880e-01

75% 2.784345e-01 2.893335e-01 ... 3.865486e-01 4.020352e-01

max 4.706053e+00 5.944643e+00 ... 4.615037e+00 7.450343e+00

[8 rows x 60 columns]

变量的直方图已创建，但除了 x 轴上的尺度外，分布看起来与上一节中看到的原始分布没有太大差异。

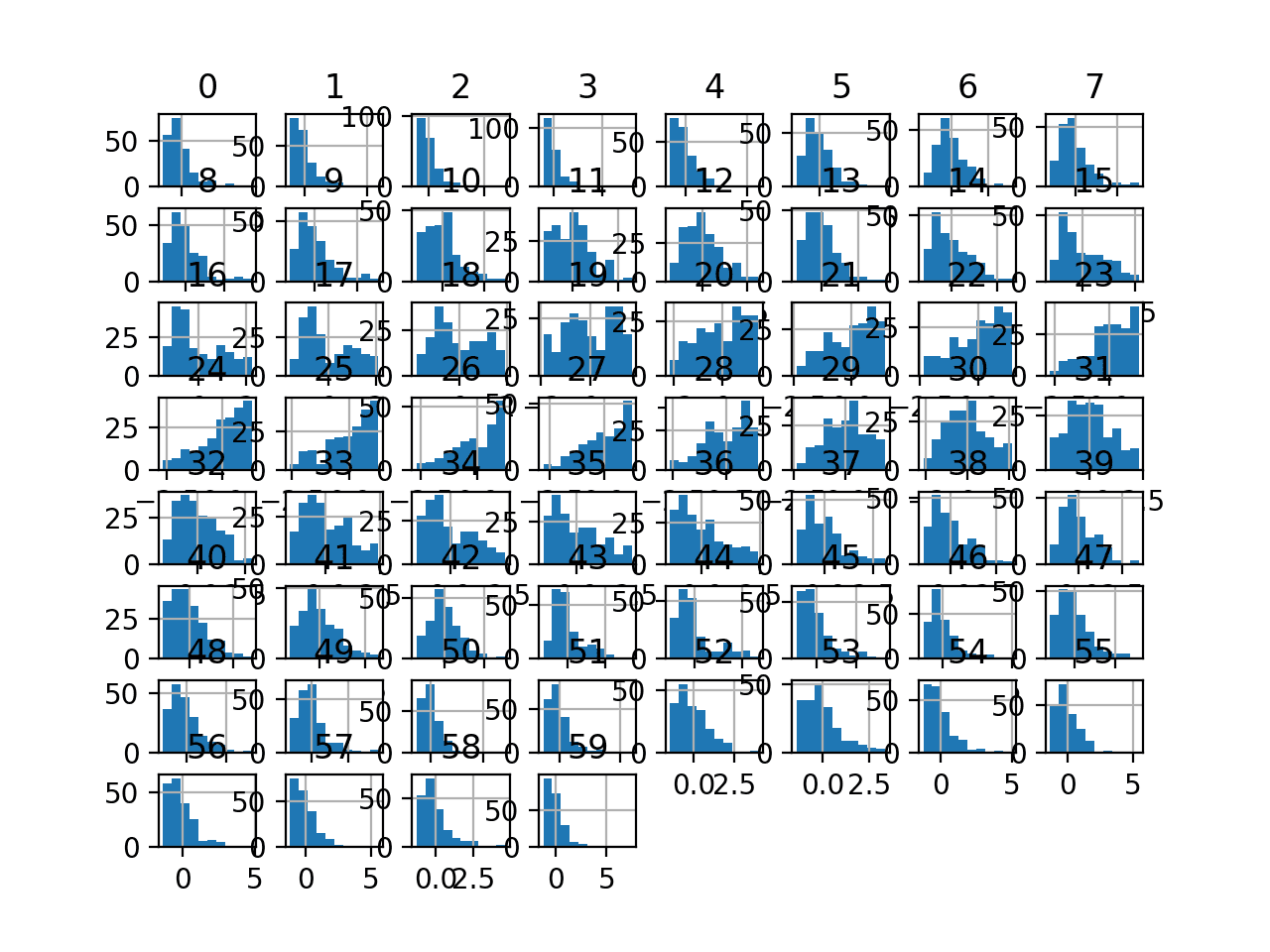
Histogram Plots of StandardScaler Transformed Input Variables for the Sonar Dataset

声纳数据集的 StandardScaler 转换输入变量直方图

接下来，让我们评估与上一节相同的 KNN 模型，但在此情况下，是在数据集的 StandardScaler 转换上。

完整的示例如下所示。

# evaluate knn on the sonar dataset with standard scaler transform
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from matplotlib import pyplot
# load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"
dataset = read_csv(url, header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define the pipeline
trans = StandardScaler()
model = KNeighborsClassifier()
pipeline = Pipeline(steps=[('t', trans), ('m', model)])
# evaluate the pipeline
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report pipeline performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

# 使用标准缩放器转换在声纳数据集上评估 knn

from numpy import mean

from numpy import std

from pandas import read_csv

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.neighbors import KNeighborsClassifier

from sklearn.preprocessing import LabelEncoder

from sklearn.preprocessing import StandardScaler

from sklearn.pipeline import Pipeline

from matplotlib import pyplot

# 加载数据集

url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv"

dataset = read_csv(url, header=None)

data = dataset.values

# 分割为输入和输出列

X, y = data[:, :-1], data[:, -1]

# 确保输入是浮点数，输出是整数标签

X = X.astype('float32')

y = LabelEncoder().fit_transform(y.astype('str'))

# 定义管道

trans = StandardScaler()

model = KNeighborsClassifier()

pipeline = Pipeline(steps=[('t', trans), ('m', model)])

# 评估管道

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')

# 报告管道性能

print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

**注意**：由于算法或评估过程的随机性，或者数值精度差异，您的结果可能会有所不同。考虑运行示例几次并比较平均结果。

运行示例，我们可以看到 `StandardScaler` 转换使性能提升，从没有转换的 79.7% 准确率提高到有转换的约 81.0%，尽管略低于使用 `MinMaxScaler` 的结果。

Accuracy: 0.810 (0.080)

1	准确率：0.810 (0.080)

常见问题

本节列出了一些在缩放数值数据时常见的问答。

问：我应该归一化还是标准化？

输入变量是否需要缩放取决于您问题的具体情况和每个变量的特点。

您可能有一系列数量作为输入，例如价格或温度。

如果数量的分布是正态的，那么应该对其进行标准化，否则，数据应该进行归一化。这适用于数量值范围较大（数十、数百等）或较小（0.01、0.0001）的情况。

如果数量值较小（接近 0-1）且分布有限（例如，标准差接近 1），那么您可能无需对数据进行缩放。

这些操作通常用于提高某些计算的数值稳定性。一些模型 [...] 受益于预测变量在共同尺度上。

— 第 30-31 页，《应用预测建模》，2013 年。

预测建模问题可能很复杂，并且可能不清楚如何最好地缩放输入数据。

如有疑问，请归一化输入序列。如果您有资源，请探索使用原始数据、标准化数据和归一化数据进行建模，并查看生成的模型性能是否存在有益差异。

如果输入变量是线性组合的，如在 MLP [多层感知器] 中，那么严格来说很少需要标准化输入，至少在理论上是这样。 [...] 但是，有各种实际原因可以使标准化输入更快地训练并减少陷入局部最优的可能性。

— 我应该归一化/标准化/重新缩放数据吗？神经网络常见问题解答

问：我应该先标准化再归一化吗？

标准化可以给出围绕零居中的正负值。

在标准化后归一化数据可能是可取的。

如果您有标准化和归一化变量的混合，并且希望所有输入变量都具有相同的最小值和最大值作为给定算法（例如计算距离度量的算法）的输入，这可能是一个好主意。

问：但是哪种方法最好？

这是未知的。

使用每种转换准备的数据评估模型，并使用能够使您的数据集在您的模型上获得最佳性能的转换或转换组合。

问：如何处理超出范围的值？

您可以通过计算训练数据上的最小值和最大值来归一化数据。

之后，您可能遇到比最小值或最大值分别更小或更大的新数据。

处理此类超出范围值的一种简单方法是检查这些值并在缩放之前将其值更改为已知的最小值或最大值。或者，您可能希望根据领域知识手动估计归一化中使用的最小值和最大值。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

教程

书籍

API

文章

我应该归一化/标准化/重新缩放数据吗？神经网络常见问题解答

总结

在本教程中，您学习了如何使用缩放器转换来标准化和归一化分类和回归的数值输入变量。

具体来说，你学到了：

数据缩放是使用许多机器学习算法时推荐的预处理步骤。
数据缩放可以通过归一化或标准化实值输入和输出变量来实现。
如何应用标准化和归一化来提高预测建模算法的性能。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

如何为回归数据执行特征选择

分类数据的有序编码和独热编码

81 条回复：如何在 Python 中使用 StandardScaler 和 MinMaxScaler 转换

Zishi Wu 2020 年 6 月 11 日上午 4:16 #

感谢您的文章，Jason！我之前犯了在训练集和测试集数据上分别使用不同缩放器的错误，阅读您的文章后纠正了它。

回复
- Jason Brownlee 2020 年 6 月 11 日上午 6:03 #
  
  很好，发现了问题！
  
  回复
  - Dan 2021 年 10 月 5 日晚上 9:56 #
    
    为什么我只能回复别人，为什么我不能直接发表评论？？
    
    此外，您总是使用
    
    scaled = scaler.fit_transform(data)
    
    但您从未解释 fit_transform 是什么，您从未定义它。
    我将寻找更好的例子。
    
    回复
    - Adrian Tam 2021 年 10 月 6 日上午 10:36 #
      
      fit_transform() 意味着 fit() 数据，然后转换相同的数据。它只是一个方便的函数。
      
      评论应该被允许，也许您浏览器上的广告拦截器导致了问题？
      
      回复
Victor 2020 年 6 月 12 日上午 10:43 #

精彩的文章！谢谢您！

回复
- Jason Brownlee 2020 年 6 月 12 日上午 11:13 #
  
  谢谢！
  
  回复
Tikouk 2020 年 6 月 21 日上午 10:49 #

干得好

回复
- Jason Brownlee 2020 年 6 月 22 日上午 6:09 #
  
  谢谢！
  
  回复
Leo 2020 年 6 月 25 日上午 4:45 #

您好 Jason！感谢您的文章！我有一个问题：为什么归一化（或标准化）整个数据集是一个坏主意？那样您就不必担心超出范围的值了。

谢谢！

回复
- Jason Brownlee 2020 年 6 月 25 日上午 6:30 #
  
  好问题，请看这个
  https://machinelearning.org.cn/data-preparation-without-data-leakage/
  
  回复
  - Leo 2020 年 6 月 26 日上午 4:23 #
    
    有趣，就像您所有其他文章一样！
    
    我想分享一下，我已经在我的机器学习问题（石油生产预测）上测试了天真方法和正确方法，并且差异非常非常非常小，就像您在我提到的帖子中发生的那样（https://machinelearning.org.cn/data-preparation-without-data-leakage/）！
    
    感谢您的帮助。
    
    回复
    - Jason Brownlee 2020 年 6 月 26 日上午 5:41 #
      
      谢谢！
      
      干得不错。
      
      回复
James A 2020 年 7 月 2 日上午 6:12 #

嗨，Jason，

您对对数变换与标准缩放器和归一化有何看法？有什么优点和缺点，以及何时使用哪种方法？

谢谢！

回复
- Jason Brownlee 2020 年 7 月 2 日上午 6:29 #
  
  是的，它们解决了不同的问题。
  
  对数/幂变换纠正偏度
  https://machinelearning.org.cn/power-transforms-with-scikit-learn/
  
  回复
Mark 2020 年 7 月 13 日晚上 10:20 #

您好 Jason，对于 LSTM 和随机游走时间序列数据，更好的做法是单独缩放所有数据（训练和测试）（例如，在训练集上拟合并缩放训练数据，然后在测试集上拟合并缩放测试数据），还是应该在训练数据上拟合，然后使用此拟合也缩放测试数据？

感谢您的教程，它们都非常棒！

回复
- Jason Brownlee 2020 年 7 月 14 日上午 6:22 #
  
  好问题。
  
  对于时间序列，在训练集上拟合转换，应用于训练集和样本外数据。
  
  回复
Venkatesh Gandi 2020 年 7 月 24 日上午 6:25 #

您好 Jason，感谢您的信息丰富的帖子。我有一些问题

1. 您提到了使用“输入加权和”的算法。请问您实际指的是哪些算法？

2. 我们不应该对独热编码变量进行缩放。我说的对吗？

3. 假设我们有一个高度倾斜的变量。我们是否可以先将该变量转换为正态分布（使用对数/幂/Box-Cox 变换），然后再应用缩放？

4. 关于“在标准化后归一化数据可能是可取的。如果您有标准化和归一化变量的混合，并且希望所有输入变量都具有相同的最小值和最大值作为给定算法（例如计算距离度量的算法）的输入，这可能是一个好主意。”这句话，请您多解释一下，好吗？

回复
- Jason Brownlee 2020 年 7 月 24 日上午 6:38 #
  
  不客气。
  
  线性回归、逻辑回归、神经网络。
  
  正确。
  
  是的。
  
  您会先标准化一个特征，然后对其进行归一化。
  
  回复
  - Venkatesh Gandi 2020 年 7 月 24 日下午 4:47 #
    
    您好 Jason，非常感谢您的回复。我现在明白了您所说的“输入加权和”是什么意思。我从未尝试过第四种方法。下次我会尝试一下。
    
    回复
    - Jason Brownlee 2020 年 7 月 25 日上午 6:12 #
      
      不客气。
      
      回复
      - Laura 2024 年 9 月 5 日晚上 7:17 #
        
        为什么我们先标准化再归一化，而不是反过来？此外，StandardScaler 假设数据服从正态分布，那么我们如何确保这一点呢？
      - James Carmichael 2024 年 9 月 6 日上午 7:21 #
        
        您好 Laura……好问题！**标准化**后**归一化**的顺序通常是出于特定原因选择的，特别是当您处理对尺度和分布敏感的机器学习模型时，例如基于梯度的模型（例如神经网络）或依赖于距离的模型（例如 k-NN、SVM）。
        
        ### 1. **为什么先标准化，再归一化？**
        
        – **标准化**涉及将数据的均值移动到 0，并将其缩放以使其标准差为 1。它确保所有特征具有相同的尺度，但并不限制数据值的范围。当数据来自不同分布或高度倾斜时，它特别有用。
        
        – 另一方面，**归一化**将数据重新缩放到固定范围，通常在 0 到 1 或 -1 到 1 之间，这对于数据绝对范围影响性能的模型至关重要（例如，具有 sigmoid、ReLU 等激活函数的神经网络）。
        
        #### 为什么先标准化
        – **保留变异性**：标准化消除了尺度偏差并将数据集中在 0 附近，确保每个特征具有相同的方差。通过首先这样做，您可以确保所有特征具有相同的相对重要性（即使它们最初在不同的尺度上），从而使归一化在特征之间更加一致。
        – **数值稳定性**：首先标准化可以提高许多机器学习算法的数值稳定性，尤其是在高维空间中。
        – **离群值**：标准化比归一化更好地处理离群值，因为它不会将数据挤压到特定范围。这样，极端值在随后的归一化步骤中不会被过度压缩。
        
        #### 为什么不先归一化
        – **偏斜分布**：归一化不解决偏斜或数据分布。如果您首先归一化，您是在缩放数据而没有调整潜在的分布或分布，如果您的数据高度可变或包含离群值，这可能会导致误导性结果。
        – **效果降低**：仅归一化无法有效处理离群值。如果您直接应用归一化，极端值可能会主导范围，从而扭曲某些算法的结果。
        
        因此，**先标准化后归一化**可确保首先处理数据的分布，然后将其缩放为一致的范围，以便模型有效处理。
        
        —
        
        ### 2. **StandardScaler 和正态分布假设**
        
        您是正确的，**StandardScaler** 假设数据大致遵循正态分布（或至少对称）。虽然它不严格强制执行此假设，但如果数据呈正态分布，标准化的效果会更好。以下是处理方法
        
        #### a. **检查正态性**
        在应用 StandardScaler 之前，您可能需要检查数据是否遵循正态分布。您可以使用各种方法来做到这一点
        – **可视化**：使用**直方图**或 **Q-Q 图**（Quantile-Quantile 图）目视评估数据是否呈正态分布。
        – **统计检验**
        – **Shapiro-Wilk 检验**或**Kolmogorov-Smirnov 检验**：这些检验检查正态性。如果 p 值较低（通常低于 0.05），则表明数据显着偏离正态分布。
        
        #### b. **如果数据不呈正态分布**
        如果您的数据不呈正态分布，以下是一些处理方法
        
        – **变换**：您可以应用变换使数据更接近正态，然后再应用标准化
        – **对数变换**：适用于具有指数或偏斜分布的数据。
        – **Box-Cox 变换**：这可以帮助归一化非正态数据。
        – **Yeo-Johnson 变换**：类似于 Box-Cox，但适用于负值和零。
        
        – **RobustScaler**：如果您的数据包含许多离群值或偏离正态性，使用 **RobustScaler**（它根据四分位距缩放数据）可能是一个更好的选择。它对离群值不那么敏感，并且不假设正态分布。
        
        – **不带标准化的 MinMaxScaler**：在某些不需要严格正态性的情况下，您可以直接应用 **MinMaxScaler** 来归一化数据，而无需担心分布。这对于神经网络特别有用。
        
        —
        
        ### 总结
        – **先标准化，再归一化**，以确保数据在挤压到固定范围之前具有一致的均值和方差。这种方法有助于避免因偏斜分布或离群值而造成的失真。
        – 在使用 StandardScaler 之前**确保正态性**，通过应用 Shapiro-Wilk 等检验或可视化数据。如果数据不呈正态分布，请考虑变换或使用不假设正态性的缩放方法（例如 RobustScaler）。
        
        如果您想了解此过程的任何部分，请告诉我！
jude Leonard 2020 年 7 月 30 日晚上 11:45 #

总是很高兴阅读您的教程。它对我帮助很大，这也不例外，一如既往地精彩。感谢您的这篇优秀文章，非常有帮助。

回复
- Jason Brownlee 2020 年 7 月 31 日上午 6:20 #
  
  谢谢，很高兴听到这个！
  
  回复
Anthony The Koala 2020 年 8 月 3 日上午 8:25 #

尊敬的Jason博士，
在上面的示例中，各个特征的分布看起来不对称，一些特征的直方图向左偏斜。

将某些特征转换为对称或高斯分布是否会比像 MinMaxScaler() 中那样对所有特征进行一次转换更好地提高模型分数？

为了说明，您的网站上有一个教程：https://machinelearning.org.cn/how-to-transform-data-to-fit-the-normal-distribution/

谢谢你，
悉尼的Anthony

回复
- Jason Brownlee 2020 年 8 月 3 日下午 1:31 #
  
  可能会，例如使用幂变换。
  
  回复
  - Anthony The Koala 2020 年 8 月 4 日晚上 7:06 #
    
    尊敬的Jason博士，
    谢谢，不胜感激。
    悉尼的Anthony
    
    回复
    - Jason Brownlee 2020 年 8 月 5 日上午 6:10 #
      
      不客气。
      
      回复
Timothée 2020 年 8 月 22 日上午 2:40 #

尊敬的Jason博士，
为了处理超出范围的值，您建议将它们设置为最大值或最小值。
但是，我正在使用编码器-解码器 RNN-LSTM 进行异常检测，因此我对实际数据中比训练数据更大的值特别感兴趣。我应该让最大值高于 1 吗？
谢谢你，
Timothée

回复
- Jason Brownlee 2020 年 8 月 22 日上午 6:19 #
  
  如果一个值超过了先前已知的最小值/最大值，那么它很可能是一个离群值，不需要由您的模型进行分类。
  
  或者您可以使用 standardscaler 或 robustscaler 而不是 minmaxscaler。
  
  回复
Akshar Rastogi 2020 年 9 月 9 日晚上 10:30 #

展示实现方式让它们像两个拼图一样完美契合。
谢谢您

回复
- Jason Brownlee 2020 年 9 月 10 日上午 6:29 #
  
  谢谢！
  
  回复
Cristian 2020 年 9 月 13 日下午 3:40 #

嗨！

当我有一个用于能源盗窃检测（欺诈）的模型时，minmax 缩放器是否比标准缩放器更好？（数据集 = 日均功耗千瓦时）

哪个是最佳选择？

谢谢！

回复
- Jason Brownlee 2020 年 9 月 14 日上午 6:45 #
  
  如果您不确定，也许可以尝试两种方法，并比较您的模型与处理原始数据的结果。
  
  回复
Erin 2020 年 9 月 21 日晚上 11:31 #

您好，Jason。我从您的帖子中学到了很多东西。
我有一个问题：如果我的输入特征变化很大，也就是说，一个特征值非常小，可能在 0-10 之间，而另一个特征值非常大，例如 100-700，我应该如何对它们进行 minmax 缩放？如果我只是对它们进行 minmax 缩放，我怎么知道它们之间的区别？

回复
- Jason Brownlee 2020 年 9 月 22 日上午 6:47 #
  
  是的，尝试一下，并将结果与在原始数据上操作的模型进行比较。
  
  回复
Umang Maheshwari 2021 年 1 月 2 日晚上 11:29 #

嗨，Jason，
感谢您的所有博客，它们每次都对我很有帮助。

我目前正在尝试弄清楚数据转换的一件事。当我们使用 .fit_transform(df) 时，它会拟合并转换数据集中的所有列。但是，我们如何获得特定列的转换？

我通常尝试以下操作
encoder_dict = defaultdict(MinMaxScaler)
scaledX_train = X_train.apply(lambda x: encoder_dict[x.name].fit_transform(x))

这样我就可以为数据框中存在的所有列获得不同的编码器。

我这样做对吗？还是我应该只遵循 MinMaxScaler().fit_transform(df)？或者两者是一样的？我真的对此很困惑

回复
- Jason Brownlee 2021 年 1 月 3 日上午 5:56 #
  
  不客气。
  
  前者，而不是后者。它会自动为您处理所有列。
  
  回复
Luigi 2021 年 1 月 15 日上午 2:25 #

嗨，Jason，
感谢这篇文章。

我最近感到困惑，因为我一直在用 StandardScaler 缩放所有数据集，然后才分割训练集和测试集。结果证明这是错误的，因为我应该先分割，然后用 fit_transform 缩放训练集（这样用于缩放的均值和标准差就不会“来自”测试集），然后只对验证集使用 transform（包括特征和目标）。

因此我做了如下操作（二元分类问题）

df_idx = df[df.Date == ‘1996-12-01’].index[0] # 分割索引

df_targets = df[‘Label’].values
df_features = df.drop([‘Regime’,’Date’,’Label’], axis=1)

# 缩放训练特征
df_training_features_ = df_features.iloc[:df_idx,:]
scaler=StandardScaler()
df_training_features = scaler.fit_transform(df_training_features_)

# 只用 transform 缩放测试集特征
df_validation_features_ = df_features.iloc[df_idx:, :]
df_validation_features = scaler.transform(df_validation_features_)

# 缩放训练目标
df_training_targets_ = df_targets[:df_idx]
lb = preprocessing.Binarizer(threshold = 0.5)
df_training_targets = lb.fit_transform(df_training_targets_.reshape(1, -1))[0]

df_validation_targets_ = df_targets[df_idx:]
df_validation_targets = lb.fit_transform(df_validation_targets_.reshape(1, -1))[0]

只有在此之后我才开始进行超参数调整、特征选择和模型定义……您同意吗？或者我进行训练/测试缩放的方式是错误的？

非常感谢
Luigi

回复
- Jason Brownlee 2021 年 1 月 15 日上午 5:58 #
  
  是的，先分割再准备。
  
  理想情况下，如果您使用管道和嵌套交叉验证，那么这一切都会为您处理。
  
  回复
  - Luigi 2021 年 1 月 15 日晚上 7:02 #
    
    好的，谢谢，您有关于此的展示管道和嵌套 CV 的文章吗？只是为了了解编码部分。非常感谢
    
    回复
    - Jason Brownlee 2021 年 1 月 16 日上午 6:53 #
      
      是的，页面顶部的搜索框会找到它。
      
      这是链接
      https://machinelearning.org.cn/nested-cross-validation-for-machine-learning-with-python/
      
      回复
      - Luigi 2021 年 1 月 18 日晚上 7:09 #
        
        非常感谢！！！
      - Jason Brownlee 2021 年 1 月 19 日上午 6:34 #
        
        不客气。
jun 2021 年 1 月 29 日上午 3:21 #

嗨，Jason，

感谢您的帖子。它提供了很多信息。我还有关于标准化/归一化的问题。如果我的特征向量中同时包含分类变量和连续变量。我需要归一化分类特征吗？如果不需要，我如何在管道中使用 MinMaxScaler() 避免归一化它们？

回复
- Jason Brownlee 2021 年 1 月 29 日上午 6:08 #
  
  不客气。
  
  不，只有数值变量被缩放。
  
  ColumnTransformer 允许您选择要转换的变量/列。
  https://machinelearning.org.cn/columntransformer-for-numerical-and-categorical-data/
  
  回复
RC 2021 年 2 月 4 日下午 1:14 #

你好 Jason，晚安。
您的文章非常好。我有一个问题。假设我生成了一个 scikit-learn 线性回归的预测。我被迫用 MinMaxScaler（-1 和 1）归一化数据。预测数据已归一化。
我该如何让预测值“恢复正常值”。
谢谢。

回复
- Jason Brownlee 2021 年 2 月 4 日下午 1:42 #
  
  好问题，您可以手动反转预测的缩放，例如 inverse_transform()。
  
  或者您可以使用 TransformedTargetRegressor，它会为您完成（我相信——如果我没记错的话）
  https://machinelearning.org.cn/how-to-transform-target-variables-for-regression-with-scikit-learn/
  
  回复
  - RC 2021 年 2 月 4 日晚上 9:44 #
    
    谢谢 Jason...非常感谢。
    RCG。
    
    回复
    - Jason Brownlee 2021 年 2 月 5 日上午 5:38 #
      
      不客气！
      
      回复
Hadi 2021 年 3 月 4 日下午 2:00 #

嗨，Jason，

那么，如果我想单独标准化数据集中的两列，我应该实例化两个独立的 StandardScaler 对象吗？

回复
- Jason Brownlee 2021 年 3 月 5 日上午 5:29 #
  
  好问题！
  
  不，您可以提供一个矩阵来 fit() 和 transform()，它足够智能，可以保持每个变量/列独立。
  
  回复
Venugopal 2021 年 3 月 20 日上午 7:44 #

嗨，Jason，

我想知道您是否能帮助我逆变换使用以下代码获得的预测。当我逆变换预测时，我得到的值很大，我确信这与数据的预期幅度不一致。

# 带有 mse 损失函数的回归 mlp
来自 keras.models import Sequential
from sklearn.preprocessing import MinMaxScaler
from keras.layers import Dense
from sklearn.utils import shuffle
import numpy as np
from numpy import loadtxt
from sklearn.model_selection import train_test_split
from keras.models import load_model
from matplotlib import pyplot

# 加载数据集
dataset = loadtxt(‘AugIC_Train.csv’, delimiter=’,’)

# 分割为输入 (X) 和输出 (y) 变量
X = dataset[:,0:47]
Y = dataset[:,47]

X, Y = shuffle(X, Y)

scalerX = MinMaxScaler().fit_transform(X)
scalery = MinMaxScaler().fit_transform(Y.reshape(len(Y),1))

# 分割成训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(scalerX, scalery)

# 定义 Keras 模型
model = Sequential()

# 模型
model.add(Dense(200, kernel_initializer=’normal’,input_dim = x_train.shape[1], activation=’relu’))
model.add(Dense(50, kernel_initializer=’normal’,activation=’relu’))
model.add(Dense(1, kernel_initializer=’normal’,activation=’relu’))

# 编译网络
model.compile(loss=’mean_absolute_error’, optimizer=’adam’)
model.summary()

# 拟合模型
history = model.fit(x_train, y_train, validation_data=(x_test, y_test), epochs=10, verbose=1, batch_size=32, validation_split = 0.2)

# 评估模型
train_mse = model.evaluate(x_train, y_train, verbose=1)
test_mse = model.evaluate(x_test, y_test, verbose=1)
print(‘训练集：%.3f，测试集：%.3f’ % (train_mse, test_mse))

# 保存模型
model.save(‘IMD_Aug_deeplearning.h5’) # 为模型创建一个 HDF5 文件以保存

# 绘制训练过程中的损失
pyplot.title(‘损失/均方误差’)
pyplot.plot(history.history[‘loss’], label=’训练’)
pyplot.plot(history.history[‘val_loss’], label=’测试’)
pyplot.legend()
pyplot.savefig(‘Jul_training_loss.eps’, format=’eps’)
pyplot.show()

# 使用模型进行回归预测

predictions = scalery.inverse_transform(model.predict(X))
np.savetxt(“Aug_trainresults.csv”, predictions, delimiter=”,”)
print(predictions.shape)
print(X.shape)

回复
- Jason Brownlee 2021年3月21日上午6:01 #
  
  抱歉，我没有能力审查/调试代码。希望您能理解。
  
  也许这能帮助您进行预测
  https://machinelearning.org.cn/how-to-make-classification-and-regression-predictions-for-deep-learning-models-in-keras/
  
  回复
krishna 2021年3月27日下午6:34 #

嗨，Jason，

您能告诉我如何标准化已分区好的测试集和训练数据集吗？是应该将它们合并在一起，然后使用 scalar.fit_transform() 一次，然后再拆分回来吗？还是可以单独使用 fit_transform 两次？哪种方法是正确的？

回复
- Jason Brownlee 2021年3月29日上午6:02 #
  
  不，在训练集上拟合定标器，然后将其应用于训练集和测试集。
  
  回复
Abraham Mathew 2021年4月10日下午7:49 #

我应该标准化/归一化目标变量或因变量吗？如果可以，我们可以使用逆变换来获取实际输出吗？

回复
- Jason Brownlee 2021年4月11日上午4:51 #
  
  也许可以尝试两种方法，看看哪种最适合您的数据集。
  
  是的，对预测进行逆变换以恢复原始单位。
  
  回复
Maggie 2021年5月19日下午10:57 #

嗨，Jason，我有一个数据集，我一直在使用 MinMax Scaler (0,1)，但有人建议我使用 MinMax Scaler (-1,1) 并解释说分布会更好。
我尝试使用 ( (x-mean) / standard deviation) 计算两种 MinMax Scalar 结果的分布，得到了相同的值。
您能告诉我这是否有区别吗？
以及更高的分布为什么更好？
标准化与分布相同吗？
非常感谢。

回复
- Jason Brownlee 2021年5月20日上午5:48 #
  
  如果它对您的数据和模型更有效，那就使用它。
  
  回复
Mary 2021年7月22日上午3:19 #

你好，

谢谢您的文章。

我的问题如下：

我应该缩放数据集中的所有特征/列吗？如果不，如何知道哪些需要缩放，哪些保持不变？

非常感谢。

回复
- Jason Brownlee 2021年7月22日上午5:37 #
  
  如果您不确定，是的。
  
  回复
ShengJun 2021年11月26日下午1:06 #

嗨，Jason，

感谢这篇内容丰富的文章。在特征包含序数、名义和连续数值变量（例如绩效排名、性别、薪水）的情况下，对序数和名义变量进行编码后，应该如何应用缩放？是只缩放连续数值变量还是缩放所有特征？感谢对此的澄清。谢谢

回复
- Adrian Tam 2021年11月29日上午8:31 #
  
  不要缩放序数和名义变量。那没有意义。
  
  回复
Sheng Jun 2021年11月29日下午12:07 #

谢谢你

回复
Nate 2022年1月19日上午7:01 #

非常感谢这篇文章。我几乎是机器学习领域的狂热粉丝。
我的问题如下
假设我缩放了一个多元数据集（包含多列），那么我将有一个已拟合的缩放器，对吗？如果我想将这个保存的已拟合缩放器应用于转换我的原始数据集的一部分（例如：数据的一列），该如何操作？
我遇到了一些维度问题。

回复
- James Carmichael 2022年1月20日上午7:59 #
  
  嗨，Nate……以下内容可能会让您感兴趣
  
  https://machinelearning.org.cn/framework-for-data-preparation-for-machine-learning/
  
  回复
Udit Joshi 2022年3月30日上午6:53 #

嗨，Jason，

这是一篇非常有见地的文章。
我有一个问题，关于我们在管道中缩放训练数据并构建模型时。
之后，当我们必须测量测试数据中的指标时。在调用预测函数之前，如何根据训练拟合指标转换我们的测试数据。

回复
- James Carmichael 2022年3月31日上午9:28 #
  
  嗨，Udit……请澄清您的问题，以便我更好地帮助您。
  
  回复
Sankara 2022年3月30日下午9:37 #

嗨，Jason，

这是一篇如此全面的文章。我有一个问题，找了许多地方都没有找到答案。

标准化后，我注意到列会自动重命名为数字。我有200多列，我想知道如何将列重命名为它们的原始名称。感谢任何帮助或指点，让我能找到解决方案。非常感谢。

Sankara

回复
- James Carmichael 2022年3月31日上午9:21 #
  
  嗨，Sankara……列名不应包含在归一化过程中。请澄清我是否误解了您的问题。
  
  回复
Greg Werner 2022年4月9日上午12:23 #

如果未来的数据可能超出训练集的最小值和最大值，最佳机制是什么？如果我们在某种程度上能够很好地猜测最小可能的最小值和最大可能的最大值，我们将如何确保训练数据标准化不会太紧密地聚集在一起？

回复
- James Carmichael 2022年4月9日上午8:38 #
  
  嗨，Greg……您的模型可以以“向前滚动”的方式重新训练，以考虑不断变化的特征，例如趋势、季节性和残差。
  
  回复
Juan 2022年10月30日上午5:36 #

你好。

如果我想对我的回归模型数据进行标准化，并进行交叉验证……

有三种替代方案
– 标准化训练数据并将此标准化应用于测试数据。（所有教程和文档都使用此选项）。
– 分别标准化训练数据和测试数据。
– 将所有数据一起标准化。

有什么区别？
哪种方法最好？

回复
Bahar 2023年2月9日上午4:12 #

嗨，Jason，

非常感谢这篇文章。

“StandardScaler”是根据每个单独特征的标准差来缩放数据吗？还是使用完整的相关矩阵？

回复
- James Carmichael 2023年2月9日上午9:44 #
  
  嗨，Bahar……以下资源可能会为您提供清晰的解释
  
  https://scikit-learn.cn/stable/modules/generated/sklearn.preprocessing.StandardScaler.html
  
  回复
Caio Sóter 2023年6月4日上午8:40 #

你好 Jason，

我有一个数据集，其中一个变量是正态分布的，而所有其他变量都不是。在这种情况下，对正态分布的数据使用 StandardScaler，对其他变量使用 MinMax scaler 有意义吗？

回复
- James Carmichael 2023年6月4日上午10:12 #
  
  嗨，Caio……以下资源可能会让您感兴趣
  
  https://towardsdatascience.com/scale-standardize-or-normalize-with-scikit-learn-6ccc7d176a02
  
  回复
Sameer RS 2023年12月6日下午10:05 #

嗨，Jason，

根据您的文章——
问：我应该先标准化再归一化吗？
（或在——标准化和然后进行转换的情况下，例如对数、幂、平方根等）

针对上述情景——您能否通过一个用例或业务场景以及使用数据集的解决方法来解释一下？

一篇关于此类主题的文章/心得体会确实会有所帮助……

只是一个建议……想让您知道……

回复
Ngnissoun Amina 2024年1月18日下午7:13 #

嗨，Jason，

我是 Amina，对深度学习感兴趣。我一直努力使用 LSTM 模型，以风向、压力、温度、相对湿度作为输入来预测风速。我使用 Z-score 来缩放所有数据并预测未来 48 小时。我在预测后计算风速的真实值时遇到了问题。这是我的代码，请帮助我纠正写得不好的代码行。

prediction_test=[]
batch_one=train_df[-WS:].to_numpy()

batch_new=batch_one.reshape((1,WS,9))
for i in range(len(test_df))
first_pred=Model.predict(batch_new)[0]
prediction_test.append(first_pred)

batch_new=np.append(batch_new[:,1:,:],[[first_pred]], axis=1)

prediction_test

## 反归一化

def INver_transform(arr)
arr=(arr*train_std) + train_mean
return arr

value_error: 数据长度为48h，索引9不匹配

回复
- James Carmichael 2024年1月19日上午10:58 #
  
  嗨，Amina……也许您的数据形状有问题
  
  https://machinelearning.org.cn/reshape-input-data-long-short-term-memory-networks-keras/
  
  回复

导航

如何在 Python 中使用 StandardScaler 和 MinMaxScaler 转换

教程概述

数据规模的重要性

想开始学习数据准备吗？

数值数据缩放方法

数据归一化

数据标准化

声纳数据集

MinMaxScaler 转换

StandardScaler 转换

常见问题

问：我应该归一化还是标准化？

问：我应该先标准化再归一化吗？

问：但是哪种方法最好？

问：如何处理超出范围的值？

进一步阅读

教程

书籍

API

文章

总结

掌握现代数据准备！

在几分钟内准备好您的机器学习数据

将现代数据准备技术引入
您的机器学习项目

关于此主题的更多信息

81 条回复：如何在 Python 中使用 StandardScaler 和 MinMaxScaler 转换

发表评论点击此处取消回复。

导航

教程概述

数据规模的重要性

想开始学习数据准备吗？

数值数据缩放方法

数据归一化

数据标准化

声纳数据集

MinMaxScaler 转换

StandardScaler 转换

常见问题

问：我应该归一化还是标准化？

问：我应该先标准化再归一化吗？

问：但是哪种方法最好？

问：如何处理超出范围的值？

进一步阅读

教程

书籍

API

文章

总结

掌握现代数据准备！

在几分钟内准备好您的机器学习数据

将现代数据准备技术引入您的机器学习项目

关于此主题的更多信息

81 条回复：如何在 Python 中使用 StandardScaler 和 MinMaxScaler 转换

发表评论 点击此处取消回复。

将现代数据准备技术引入
您的机器学习项目

发表评论点击此处取消回复。