数据的样本将形成一个分布,而迄今为止最广为人知的分布是高斯分布,通常称为正态分布。
该分布提供了一个参数化的数学函数,该函数可用于计算样本空间中任何单个观测值的概率。该分布描述了观测值的聚集或密度,称为概率密度函数。我们还可以计算观测值等于或小于给定值的概率。这些观测值之间关系的摘要称为累积分布函数。
在本教程中,您将了解高斯分布及相关分布函数,以及如何计算每个分布的概率和累积分布函数。
完成本教程后,您将了解:
- 对标准分布的初步介绍,用于总结观测值之间的关系。
- 如何计算和绘制高斯分布的概率和密度函数。
- 与高斯分布相关的学生 t 分布和卡方分布。
开始您的项目,阅读我的新书 《机器学习统计学》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。

统计数据分布入门
照片由 Ed Dunens 拍摄,保留部分权利。
教程概述
本教程分为4个部分,它们是:
- 分布
- 高斯分布
- 学生 t 分布
- 卡方分布
需要机器学习统计学方面的帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
分布
从实践角度来看,我们可以将分布视为一个描述样本空间中观测值之间关系的函数。
例如,我们可能对人类的年龄感兴趣,其中个体年龄代表域中的观测值,0 到 125 岁是样本空间的范围。分布是一个数学函数,描述了不同身高观测值之间的关系。
分布只不过是变量上的一系列数据或分数。通常,这些分数按从最小到最大的顺序排列,然后可以以图形方式呈现。
— 第 6 页,《通俗统计学》,第三版,2010 年。
许多数据符合众所周知且易于理解的数学函数,例如高斯分布。可以通过修改函数参数(例如高斯分布的均值和标准差)来使函数拟合数据。
一旦知道了分布函数,就可以将其用作描述和计算相关量(例如观测值的似然度)以及绘制域中观测值之间关系的简写。
密度函数
分布通常根据其密度或密度函数来描述。
密度函数是描述数据比例或观测值比例的似然度如何在分布范围内变化的函数。
密度函数的两种类型是概率密度函数和累积分布函数。
- 概率密度函数:计算观察到给定值的概率。
- 累积分布函数:计算观测值等于或小于某个值的概率。
概率密度函数(PDF)可用于计算分布中给定观测值的似然度。它还可以用于总结分布样本空间中观测值的似然度。PDF 的图表显示了分布熟悉的形状,例如高斯分布的钟形曲线。
分布通常根据其概率密度函数及其相关参数来定义。
累积分布函数(CDF)是另一种思考观测值似然度的方式。与 PDF 计算给定观测值的似然度不同,CDF 计算观测值及其之前所有观测值的累积似然度。它可以让您快速了解并评论在给定值之前和之后分布的占比。CDF 通常绘制为分布从 0 到 1 的曲线。
PDF 和 CDF 都是连续函数。离散分布的 PDF 的等价物称为概率质量函数(PMF)。
接下来,我们将研究高斯分布以及在使用统计方法时会遇到的其他两个与高斯分布相关的分布。我们将依次查看它们的参数、概率和累积分布函数。
高斯分布
高斯分布以卡尔·弗里德里希·高斯命名,是统计学领域的大部分重点。
许多领域的数据惊人地可以用高斯分布来描述,以至于该分布通常被称为“正态”分布,因为它非常普遍。
高斯分布可以使用两个参数来描述
- 均值:用希腊小写字母 mu 表示,是分布的期望值。
- 方差:用希腊小写字母 sigma 的平方表示(因为变量的单位被平方了),描述了观测值与均值的离散程度。
通常使用方差的归一化计算,称为标准差
- 标准差:用希腊小写字母 sigma 表示,描述了观测值与均值的归一化离散程度。
我们可以通过 norm SciPy 模块 来处理高斯分布。norm.pdf() 函数可用于创建具有给定样本空间、均值和标准差的高斯概率密度函数。
下面的示例创建了一个高斯 PDF,其样本空间为 -5 到 5,均值为 0,标准差为 1。均值和标准差具有这些值的高斯分布称为标准高斯分布。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 绘制高斯分布 PDF from numpy import arange from matplotlib import pyplot from scipy.stats import norm # 定义分布参数 sample_space = arange(-5, 5, 0.001) mean = 0.0 stdev = 1.0 # 计算 PDF pdf = norm.pdf(sample_space, mean, stdev) # 绘图 pyplot.plot(sample_space, pdf) pyplot.show() |
运行示例会创建一个折线图,显示 x 轴上的样本空间,y 轴上的每个值的似然度。折线图显示了高斯分布熟悉的钟形。
钟形的顶部显示了分布中最可能的值,称为期望值或均值,在本例中为零,正如我们在创建分布时所指定的。
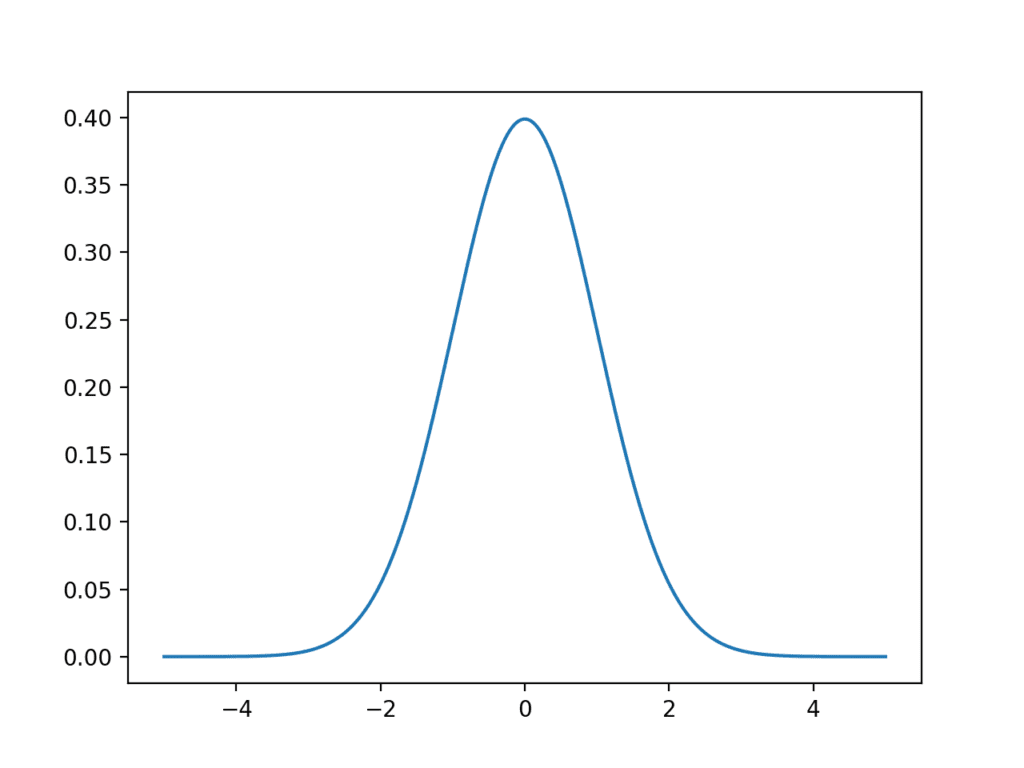
高斯概率密度函数的折线图
norm.cdf() 函数可用于创建高斯累积分布函数。
下面的示例为相同的样本空间创建高斯 CDF。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 绘制高斯分布 CDF from numpy import arange from matplotlib import pyplot from scipy.stats import norm # 定义分布参数 sample_space = arange(-5, 5, 0.001) # 计算 CDF cdf = norm.cdf(sample_space) # 绘图 pyplot.plot(sample_space, cdf) pyplot.show() |
运行示例会创建一个 S 形图,x 轴为样本空间,y 轴为累积概率。
我们可以看到,值为 2 覆盖了近 100% 的观测值,只有很小的尾部分布超出该点。
我们还可以看到,均值零表示 50% 的观测值在该点之前和之后。
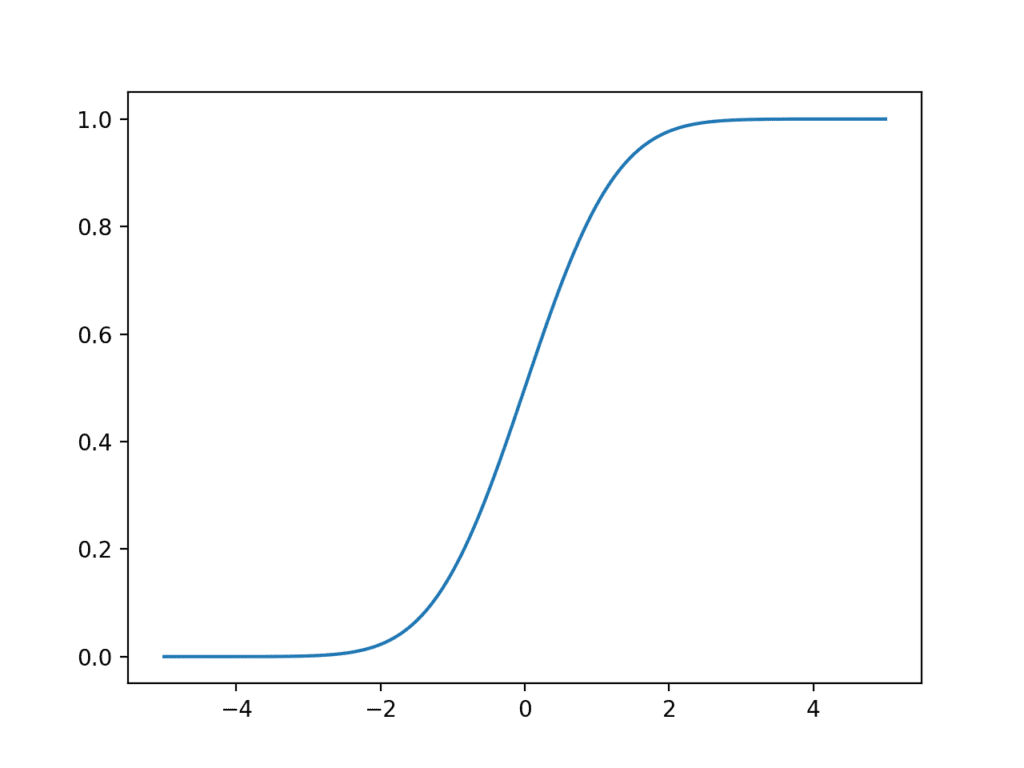
高斯累积分布函数的折线图
学生 t 分布
学生 t 分布,简称 t 分布,以威廉·西利·戈塞特(William Sealy Gosset)的笔名“学生”命名。
它是在尝试用不同大小的样本估计正态分布的均值时出现的分布。因此,在描述来自高斯分布的数据的总体统计量估计的不确定性或误差时,它是一个有用的捷径,前提是必须考虑样本的大小。
虽然您可能不会直接使用学生 t 分布,但您可能会估计来自该分布的值,这些值是其他统计方法(如统计显著性检验)的参数。
该分布可以使用一个参数来描述
- 自由度:用希腊小写字母 nu (v) 表示,表示自由度。
t 分布使用的关键是了解所需的自由度。
自由度描述了用于描述总体数量的信息量。例如,均值有 n 个自由度,因为样本中的所有 n 个观测值都用于计算总体均值的估计值。在计算样本方差时使用均值,需要从自由度中减去 1。
学生 t 分布中的观测值是根据正态分布中的观测值计算的,以描述正态分布中总体均值的区间。观测值计算如下:
|
1 |
data = (x - mean(x)) / S / sqrt(n) |
其中 x 是来自高斯分布的观测值,mean 是 x 的平均观测值,S 是标准差,n 是观测值的总数。生成的观测值形成具有 (n – 1) 自由度的 t 观测值。
在实践中,如果您在统计量的计算中需要 t 分布的值,那么自由度很可能是 n – 1,其中 n 是从高斯分布中抽取的样本大小。
您为特定问题使用的具体分布取决于您的样本大小。
— 第 93 页,《通俗统计学》,第三版,2010 年。
SciPy 在 stats.t 模块中提供了处理 t 分布的工具。t.pdf() 函数可用于创建具有指定自由度的学生 t 分布。
下面的示例使用 -5 到 5 的样本空间和 (10,000 – 1) 的自由度创建了一个 t 分布。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 绘制 t 分布 PDF from numpy import arange from matplotlib import pyplot from scipy.stats import t # 定义分布参数 sample_space = arange(-5, 5, 0.001) dof = len(sample_space) - 1 # 计算 PDF pdf = t.pdf(sample_space, dof) # 绘图 pyplot.plot(sample_space, pdf) pyplot.show() |
运行示例会创建并绘制 t 分布 PDF。
我们可以看到分布与正态分布非常相似的钟形。一个关键的区别是分布的尾部更肥厚,突出了与高斯分布相比,尾部观测值的可能性更高。
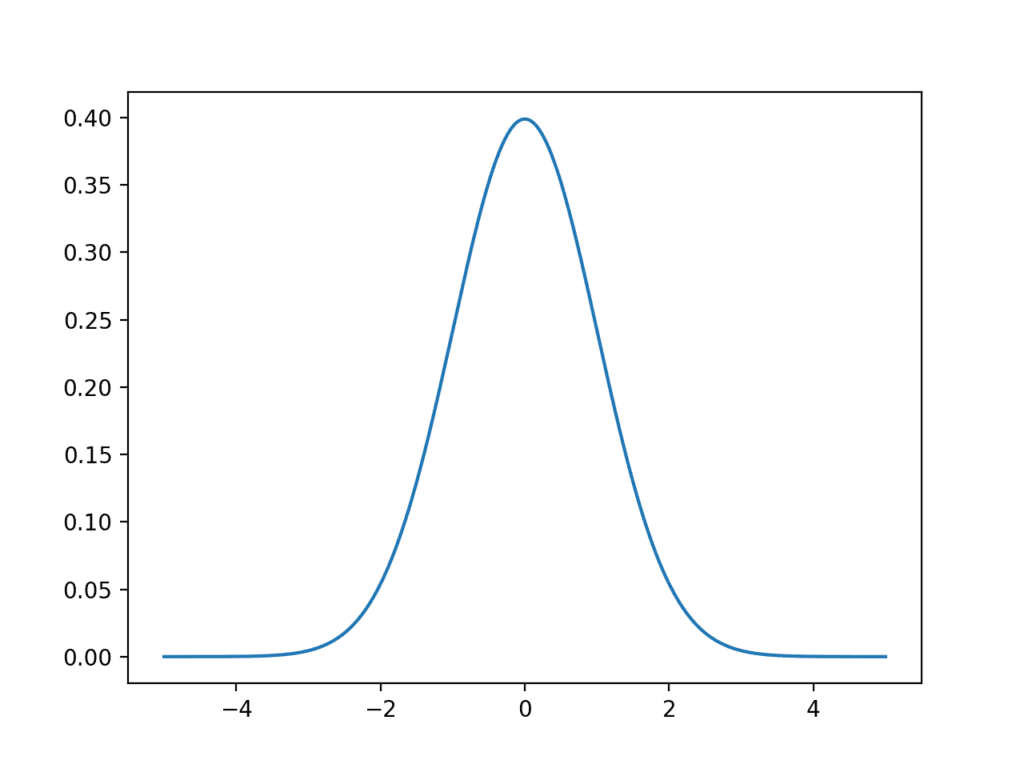
学生 t 分布概率密度函数的折线图
t.cdf() 函数可用于创建 t 分布的累积分布函数。下面的示例在与上面相同的范围内创建了 CDF。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 绘制 t 分布 CDF from numpy import arange from matplotlib import pyplot from scipy.stats import t # 定义分布参数 sample_space = arange(-5, 5, 0.001) dof = len(sample_space) - 1 # 计算 CDF cdf = t.cdf(sample_space, dof) # 绘图 pyplot.plot(sample_space, cdf) pyplot.show() |
运行示例,我们看到与高斯分布相似的 S 形曲线,尽管由于尾部更肥厚,从零概率到一概率的过渡稍微平滑一些。
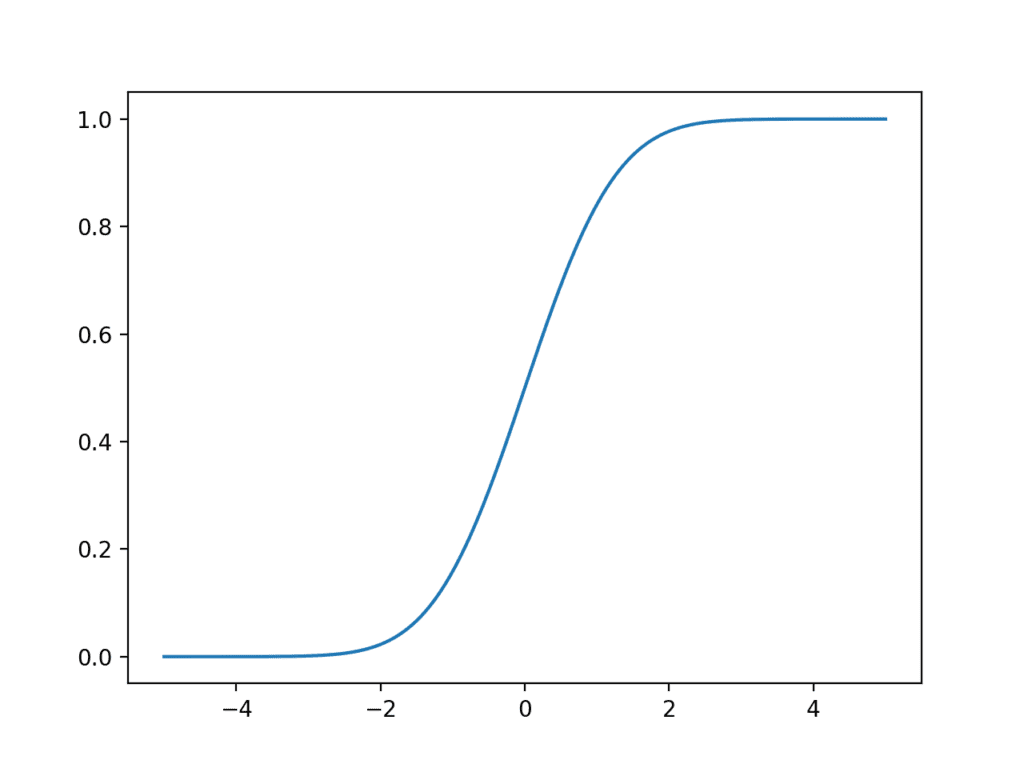
学生 t 分布累积分布函数的折线图
卡方分布
卡方分布用希腊字母 chi (X) 的小写字母的平方 (X^2) 来表示。
与学生 t 分布类似,卡方分布也用于高斯分布数据的统计方法中,以量化不确定性。例如,卡方分布用于独立性卡方检验。事实上,卡方分布用于推导学生 t 分布。
卡方分布有一个参数
- 自由度,表示为 k。
卡方分布中的一个观测值计算为从高斯分布中抽取的 k 个平方观测值的总和。
|
1 |
chi = sum x[i]^2 for i=1 to k。 |
其中 chi 是具有卡方分布的观测值,x 是从高斯分布中抽取的观测值,k 是 x 观测值的数量,这也是卡方分布的自由度。
同样,与学生 t 分布一样,数据不符合卡方分布;相反,在计算高斯数据样本的统计方法时,会从该分布中抽取观测值。
SciPy 提供了 stats.chi2 模块来计算卡方分布的统计量。chi2.pdf() 函数可用于计算样本空间在 0 到 50 之间、自由度为 20 的卡方分布。请记住,平方值的总和必须为正,因此需要正的样本空间。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 绘制卡方分布 PDF from numpy import arange from matplotlib import pyplot from scipy.stats import chi2 # 定义分布参数 sample_space = arange(0, 50, 0.01) dof = 20 # 计算 PDF pdf = chi2.pdf(sample_space, dof) # 绘图 pyplot.plot(sample_space, pdf) pyplot.show() |
运行示例会计算卡方分布 PDF 并将其显示为折线图。
自由度为 20 时,我们可以看到分布的期望值略低于样本空间中的 20。如果考虑到高斯分布的大部分密度位于 -1 和 1 之间,然后从标准高斯分布中抽取的平方随机观测值的总和将小于自由度(本例中为 20),这是符合直觉的。
尽管该分布具有类似钟形的形状,但该分布不是对称的。
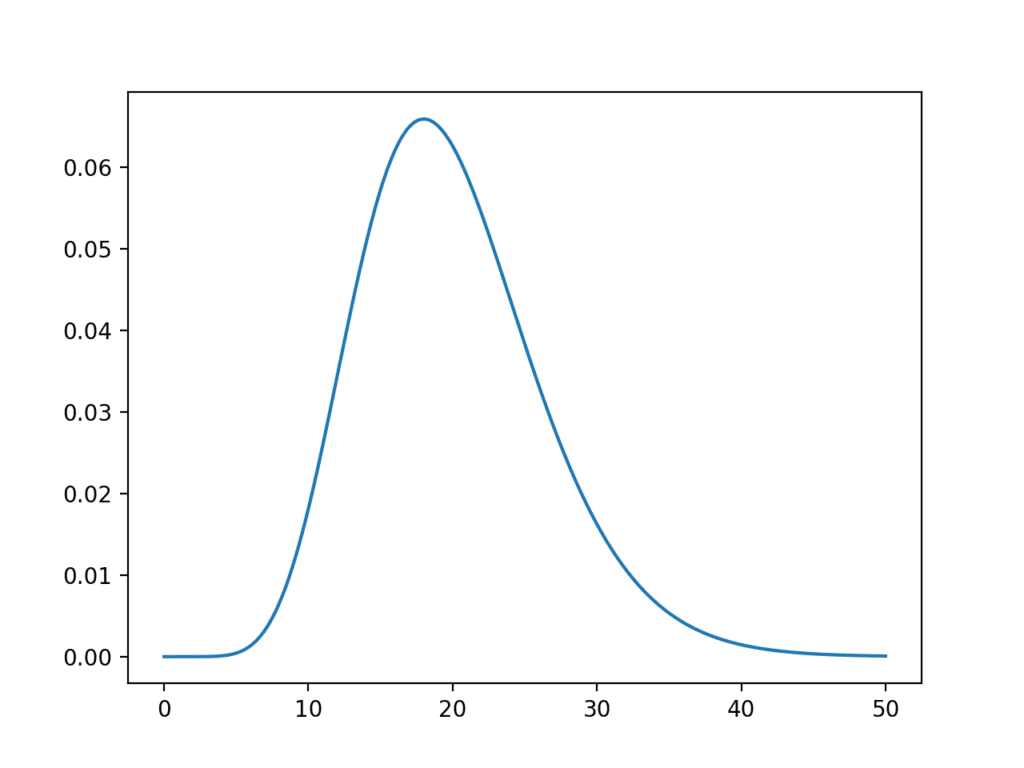
卡方分布概率密度函数的折线图
chi2.cdf() 函数可用于计算相同样本空间上的累积分布函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 绘制卡方分布 CDF from numpy import arange from matplotlib import pyplot from scipy.stats import chi2 # 定义分布参数 sample_space = arange(0, 50, 0.01) dof = 20 # 计算 CDF cdf = chi2.cdf(sample_space, dof) # 绘图 pyplot.plot(sample_space, cdf) pyplot.show() |
运行示例会创建一个卡方分布累积分布函数的图。
该分布有助于了解卡方值在 20 附近的可能性,分布右侧的肥厚尾部将远远超出图的末端。
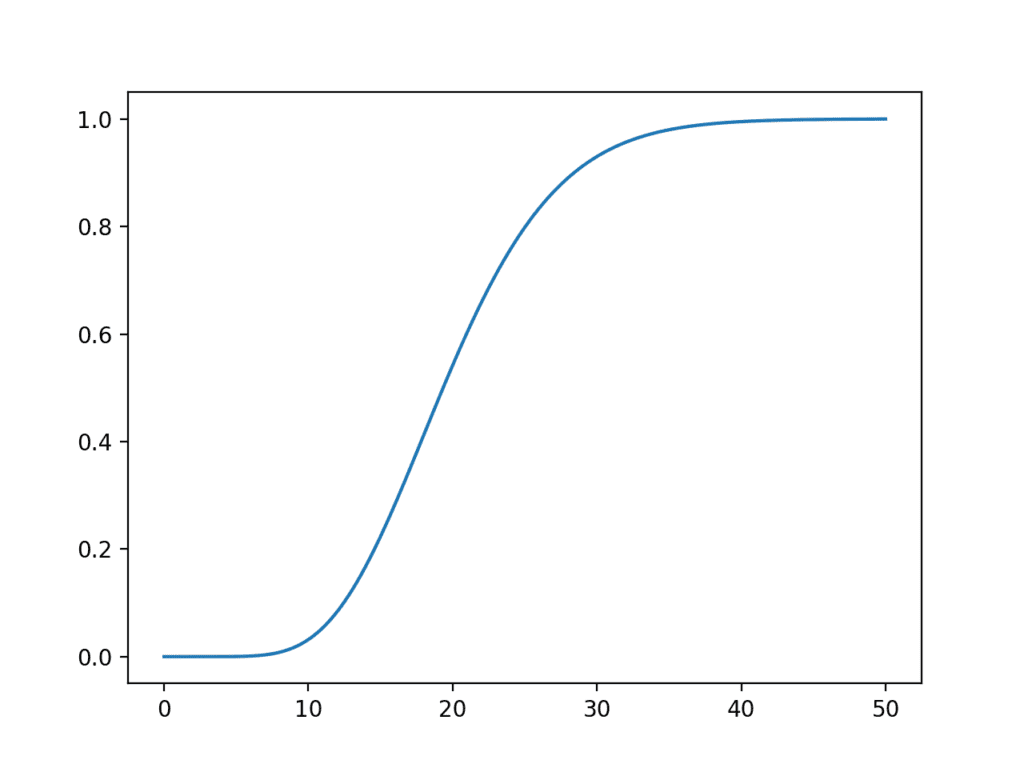
卡方分布累积分布函数的折线图
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 为一种分布使用新的样本空间重新创建 PDF 和 CDF 图。
- 计算并绘制柯西分布和拉普拉斯分布的 PDF 和 CDF。
- 从零开始查找并实现一种分布的 PDF 和 CDF 方程。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 《通俗统计学》,第三版,2010 年。
API
文章
总结
在本教程中,您了解了高斯分布及相关分布函数,以及如何计算每个分布的概率和累积分布函数。
具体来说,你学到了:
- 对标准分布的初步介绍,用于总结观测值之间的关系。
- 如何计算和绘制高斯分布的概率和密度函数。
与高斯分布相关的学生 t 分布和卡方分布。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





尊敬的Jason博士,
这个问题是关于卡方分布的。
(1) 在 t 检验中,dof = len(data)-1。卡方分布的 dof 的依据是什么?
(2) sum(observation**2) 服从卡方分布。当你可以使用高斯分布或 t 分布对未平方的观测值进行推断时,为什么要对所有观测值进行平方和求和?
谢谢你,
悉尼的Anthony
好问题,也许这里是个深入探讨的好地方
https://en.wikipedia.org/wiki/Chi-squared_distribution
尊敬的Jason博士,
我已阅读此文章。卡方检验用于多种假设检验。与使用高斯分布或卡方分布对高斯变量进行假设检验的问题有关,我引用文章中的话:“所以任何可以使用正态分布进行假设检验的地方,都可以使用卡方分布。”
也就是说,对于一组数据,如果它们服从或近似服从正态分布,则可以使用高斯分布或卡方分布方法计算假设检验。
但是,问题仍然没有回答为什么在上述博客中,当有 50 个数据点时,选择 20 个 dof。
阅读文章后,引发了进一步的问题:当对单个数据数组进行假设检验时,使用卡方检验要检验的零假设是什么?
谢谢你
悉尼的Anthony
单样本卡方检验用于确定观测频率是否与期望频率匹配。
尊敬的Jason博士,
感谢您的回复。我确实理解了观察值和期望值(根据维基百科文章)的概念,这在分类数据中使用。
但是,根据“卡方分布”处的代码,您有 5000 个观测值,但自由度为 20。您是如何从 5000 个观测值中选择 20 个自由度的?
谢谢你,
新南威尔士州的安东尼
我在文章的该部分进行了说明
在代码示例中,我们固定了 dof。
尊敬的Jason博士,
我现在明白了。变量 sample_space 是卡方分布的随机变量。自由度是概率存在的最大值。您创建了 5000 个点以使图形更平滑。
为了说明峰值/最大值就是自由度
生成两个样本卡方空间,0 到 50(5000 个点)和 0 到 100(10000 个点),每个自由度为 20。
如果绘制这两个图,您将看到最大值发生在 20 个自由度时。
为给定样本空间绘制不同自由度(例如 10、20、30、40)的图。
注意每条曲线的最大值出现在自由度处。自由度越小,最大值越大。
来源文章: http://maxwell.ucsc.edu/~drip/133/ch4.pdf ,第 2 页
谢谢你,
悉尼的Anthony
是的。
你好,Jason
您能给我一些链接,让我可以通过代码示例和真实数据来学习高斯分布吗?
上面给出的代码让我感到困惑,我需要通过真实数据来理解。
是的,请看这个
https://machinelearning.org.cn/continuous-probability-distributions-for-machine-learning/
嗨,Jason,
高斯分布在机器学习中的相关性是什么?为什么当数据分布为高斯分布或类高斯分布时,机器学习模型的表现更好?
谢谢
线性模型可能假设高斯分布,或者在数据是高斯分布时表现更好。知道我们有高斯变量有助于选择数据预处理方法,例如,标准化而不是归一化。