统计功效是指在存在真实效应时,假设检验能够检测到该效应的概率。
功效可以被计算和报告给已完成的实验,以说明对研究结果所下结论的信心程度。它还可以作为工具来估计在实验中检测到一个效应所需的观察次数或样本量。
在本教程中,您将了解统计功效在假设检验中的重要性,以及如何在实验设计中计算功效分析和功效曲线。
完成本教程后,您将了解:
- 统计功效是指假设检验在存在可被发现的效应时能够发现该效应的概率。
- 功效分析可用于估计实验所需的最小样本量,前提是设定了期望的显著性水平、效应大小和统计功效。
- 如何在 Python 中计算和绘制 Student’s t 检验的功效分析,以便有效地设计实验。
启动您的项目,阅读我的新书《机器学习统计学》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。

Python 中统计功效和功效分析的入门指南
照片由 Kamil Porembiński 拍摄,保留部分权利。
教程概述
本教程分为四个部分;它们是
- 统计假设检验
- 什么是统计功效?
- 功效分析
- Student’s t 检验功效分析
需要机器学习统计学方面的帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
统计假设检验
统计假设检验对结果做出一个假设,称为零假设。
例如,Pearson 相关检验的零假设是没有两个变量之间的关系。Student’s t 检验的零假设是两个总体的均值没有差异。
该检验通常使用 p 值进行解释,p 值是在零假设为真的情况下观察到结果的概率,而不是反过来,这常常导致误解。
- p 值 (p):获得与数据中观察到的结果相同或更极端结果的概率。
在解释显著性检验的 p 值时,必须指定一个显著性水平,通常称为希腊字母小写字母 alpha (a)。显著性水平的常见值是 5%,写为 0.05。
p 值在选定的显著性水平的背景下进行解释。当 p 值小于显著性水平时,则称显著性检验的结果“统计显著”。这意味着零假设(即不存在结果)被拒绝。
- p <= alpha:拒绝 H0,分布不同。
- p > alpha:不拒绝 H0,分布相同。
其中
- 显著性水平 (alpha):在解释 p 值时用于指定统计显著发现的边界。
我们可以看到 p 值只是一个概率,实际上结果可能不同。检验可能是错误的。根据 p 值,我们可能会在解释中出错。
有两种错误;它们是:
- 第一类错误 (Type I Error)。在实际上没有显著效应时拒绝零假设(假阳性)。p 值乐观地偏小。
- 第二类错误 (Type II Error)。在存在显著效应时未拒绝零假设(假阴性)。p 值悲观地偏大。
在这种情况下,我们可以将显著性水平视为在零假设为真时拒绝它的概率。即犯第一类错误的概率,或假阳性的概率。
什么是统计功效?
统计功效,或假设检验的功效,是指检验正确拒绝零假设的概率。
也就是说,真实阳性结果的概率。它仅在拒绝零假设时才有用。
…统计功效是指当零假设为假时,检验将正确拒绝它的概率。统计功效仅在零假设为假时才有意义。
— 第 60 页,效应大小解读指南:统计功效、元分析和研究结果的解释,2010。
对于给定实验,统计功效越高,犯第二类错误(假阴性)的概率就越低。也就是说,当存在效应时检测到效应的概率就越高。事实上,功效恰好是第二类错误概率的倒数。
|
1 2 |
功效 = 1 - 第二类错误 Pr(真阳性) = 1 - Pr(假阴性) |
更直观地说,统计功效可以被视为当备择假设为真时接受备择假设的概率。
在解释统计功效时,我们寻求具有高统计功效的实验设置。
- 低统计功效:犯第二类错误的风险大,例如假阴性。
- 高统计功效:犯第二类错误的风险小。
统计功效过低的实验结果会导致关于结果意义的无效结论。因此,必须寻求最低统计功效水平。
通常会设计统计功效为 80% 或更高的实验,例如 0.80。这意味着有 20% 的概率遇到第二类错误。这与标准显著性水平的 5% 概率遇到第一类错误不同。
功效分析
统计功效是包含四个相关部分的一个谜题;它们是:
- 效应大小 (Effect Size)。总体中存在的量化结果的幅度。效应大小使用特定的统计量度来计算,例如变量之间关系的 Pearson 相关系数,或组间差异的 Cohen's d。可以通过 Python 中的效应大小度量 进行计算。
- 样本量 (Sample Size)。样本中的观察次数。
- 显著性 (Significance)。统计检验中使用的显著性水平,例如 alpha。通常设为 5% 或 0.05。
- 统计功效 (Statistical Power)。当备择假设为真时,接受它的概率。
所有这四个变量都是相互关联的。例如,更大的样本量可以使效应更容易被检测到,并且通过提高显著性水平可以在检验中增加统计功效。
功效分析涉及在给定三个其他参数值的情况下估计其中一个参数。这在我们需要使用统计假设检验来解释的实验设计和分析中都是一个强大的工具。
例如,可以在给定效应大小、样本量和显著性水平的情况下估计统计功效。或者,可以根据不同的期望显著性水平来估计样本量。
功效分析可以回答“我的研究有多少统计功效?”和“我需要多大的样本量?”之类的问题。
— 第 56 页,效应大小解读指南:统计功效、元分析和研究结果的解释,2010。
也许功效分析最常见的用途是估计实验所需的最小样本量。
功效分析通常在研究进行之前进行。前瞻性或先验功效分析可用于估计任何一个功效参数,但最常用于估计所需的样本量。
— 第 57 页,效应大小解读指南:统计功效、元分析和研究结果的解释,2010。
作为从业者,我们可以从合理的默认参数开始,例如显著性水平 0.05 和功效水平 0.80。然后,我们可以估计一个对正在进行的实验特有的、期望的最小效应大小。然后可以使用功效分析来估计所需的最小样本量。
此外,还可以执行多个功效分析,以提供一个参数相对于另一个参数的曲线,例如实验中效应大小的变化,取决于样本量的变化。还可以创建更精细的图表,改变其中三个参数。这是实验设计的有用工具。
Student’s t 检验功效分析
我们可以通过一个实际例子来具体说明统计功效和功效分析的概念。
在本节中,我们将探讨 Student’s t 检验,这是一种用于比较来自两个高斯变量样本的均值的统计假设检验。该检验的假设或零假设是样本总体具有相同的均值,例如样本之间没有差异,或者样本来自同一个潜在总体。
该检验将计算一个 p 值,该 p 值可以解释为样本是否相同(不拒绝零假设),或者样本之间是否存在统计学上的显著差异(拒绝零假设)。解释 p 值的常见显著性水平是 5% 或 0.05。
- 显著性水平 (alpha):5% 或 0.05。
比较两个组的效应大小可以用效应大小度量来量化。用于比较两组均值差异的常见度量是 Cohen's d 度量。它计算一个标准分数,该分数以均值差异的标准差数量来描述差异。Cohen's d 的大效应大小为 0.80 或更高,这在使用该度量时通常是可以接受的。
- 效应大小:Cohen's d 至少为 0.80。
我们可以使用默认值,并假设最小统计功效为 80% 或 0.8。
- 统计功效:80% 或 0.80。
对于具有这些默认值的给定实验,我们可能对估计合适的样本量感兴趣。也就是说,为了至少检测到 0.80 的效应,并且在效应确实存在时有 80% 的机会检测到该效应(第二类错误率为 20%),以及在不存在此类效应时有 5% 的机会检测到该效应(第一类错误),每个样本需要多少观察值。
我们可以通过功效分析来解决这个问题。
statsmodels 库提供了 TTestIndPower 类,用于计算独立样本 Student’s t 检验的功效分析。值得注意的是 TTestPower 类,它可以对配对 Student’s t 检验执行相同的分析。
可以使用 solve_power() 函数来计算功效分析中的四个参数之一。在我们的例子中,我们对计算样本量感兴趣。我们可以通过提供我们已知的三个信息(alpha、effect 和 power)来使用该函数,并将我们希望计算答案的参数(nobs1)设置为“None”。这会告诉函数要计算什么。
关于样本量的一个说明:该函数有一个名为 ratio 的参数,它表示一个样本到另一个样本的样本数量之比。如果预计两个样本具有相同的观察次数,则比率为 1.0。如果,例如,预计第二个样本的观察次数只有一半,则比率将为 0.5。
必须创建 TTestIndPower 实例,然后我们可以调用 solve_power() 并传入我们的参数来估计实验所需的样本量。
|
1 2 3 |
# 执行功效分析 analysis = TTestIndPower() result = analysis.solve_power(effect, power=power, nobs1=None, ratio=1.0, alpha=alpha) |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 |
# 通过功效分析估算样本量 from statsmodels.stats.power import TTestIndPower # 功效分析参数 effect = 0.8 alpha = 0.05 power = 0.8 # 执行功效分析 analysis = TTestIndPower() result = analysis.solve_power(effect, power=power, nobs1=None, ratio=1.0, alpha=alpha) print('样本量: %.3f' % result) |
运行该示例将计算并打印出实验所需的样本量估计值为 25。这将是为在期望效应大小下看到效应所需的最小样本量。
|
1 |
样本量: 25.525 |
我们可以更进一步,计算功效曲线。
功效曲线是折线图,显示变量(如效应大小和样本量)的变化如何影响统计检验的功效。
可以使用 plot_power() 函数来创建功效曲线。因变量(x 轴)必须在 ‘dep_var‘ 参数中按名称指定。然后可以为样本量(nobs)、效应大小(effect_size)和显著性(alpha)参数指定值数组。然后将绘制一个或多个曲线,显示对统计功效的影响。
例如,我们可以假设显著性为 0.05(该函数的默认值),并探讨样本量在 5 到 100 之间变化对低、中、高效应大小的影响。
|
1 2 3 |
# 从多个功效分析计算功效曲线 analysis = TTestIndPower() analysis.plot_power(dep_var='nobs', nobs=arange(5, 100), effect_size=array([0.2, 0.5, 0.8])) |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 计算样本量和效应大小变化的功效曲线 from numpy import array from matplotlib import pyplot from statsmodels.stats.power import TTestIndPower # 功效分析参数 effect_sizes = array([0.2, 0.5, 0.8]) sample_sizes = array(range(5, 100)) # 从多个功效分析计算功效曲线 analysis = TTestIndPower() analysis.plot_power(dep_var='nobs', nobs=sample_sizes, effect_size=effect_sizes) pyplot.show() |
运行该示例将创建图表,显示样本量(x 轴)增加时,三种不同效应大小(es)下的统计功效(y 轴)的变化。
我们可以看到,如果我们对较大的效应感兴趣,那么统计功效的收益递减点大约在 40 到 50 个观察值。
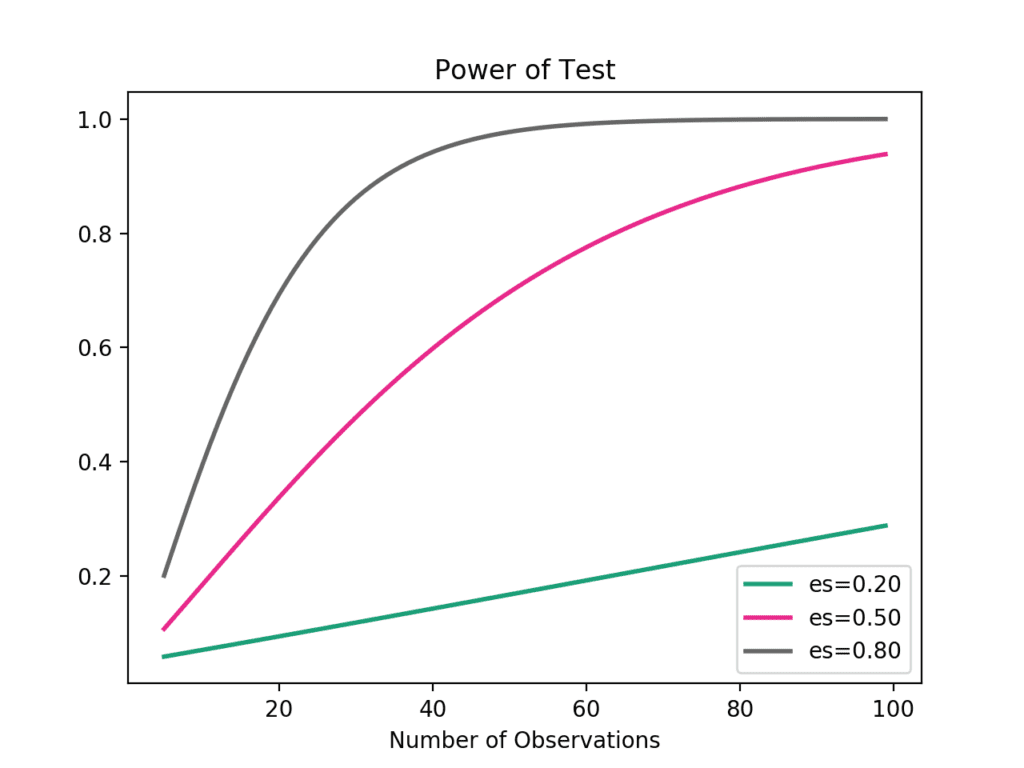
Student’s t 检验功效曲线
值得庆幸的是,statsmodels 提供了执行功效分析的类,可用于 F 检验、Z 检验和卡方检验等其他统计检验。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 绘制不同标准显著性水平相对于样本量的功效曲线。
- 查找一篇报告了实验统计功效的研究示例。
- 准备 statsmodels 提供的其他统计检验的功效分析示例。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- 效应大小——或者为什么 p 值不够, 2012.
书籍
- 效应量基本指南:统计功效、元分析与研究结果解读, 2010.
- 理解新统计学:效应量、置信区间和元分析, 2011.
- 行为科学统计功效分析, 1988.
- 行为科学应用功效分析, 2010.
API
- Statsmodels 功效和样本量计算
- statsmodels.stats.power.TTestPower API
- statsmodels.stats.power.TTestIndPower
- statsmodels.stats.power.TTestIndPower.solve_power() API
statsmodels.stats.power.TTestIndPower.plot_power() API - Statsmodels 中的统计功效, 2013.
- Statsmodels 中的功效图, 2013.
文章
总结
在本教程中,您了解了假设检验的统计功效,以及如何在实验设计中计算功效分析和功效曲线。
具体来说,你学到了:
- 统计功效是指假设检验在存在可被发现的效应时能够发现该效应的概率。
- 功效分析可用于估计实验所需的最小样本量,前提是设定了期望的显著性水平、效应大小和统计功效。
- 如何在 Python 中计算和绘制 Student’s t 检验的功效分析,以便有效地设计实验。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





很棒的文章,谢谢。
谢谢。
一如既往的好文章…
谢谢。
优秀
谢谢。
很棒的文章,感谢您从机器学习的角度探讨这个重要但常被忽视的主题。但有一个问题;在这句话“统计功效可以通过提高显著性水平来提高”中,您是指通过降低显著性水平(即,降低 alpha)来提高功效吗?也许“显著性水平”这个词的用法有误导性。
我认为您说得对。已修正。谢谢 Phil。
原始陈述可能是正确的。更高的显著性水平可能意味着更小的零假设接受区域,接受备择假设的概率更高,从而增加了统计功效。参考:https://support.minitab.com/en-us/minitab-express/1/help-and-how-to/basic-statistics/inference/supporting-topics/basics/increase-the-power-of-a-hypothesis-test/,https://stattrek.com/hypothesis-test/power-of-test.aspx
感谢分享。
我也同意这一点,Jason,它应该写成“统计功效可以通过提高显著性水平来提高”。
此外,您说:
“[统计功效] 仅在拒绝零假设时才有用。”
但您引用了《效应大小解读指南》,其中说:
“统计功效仅在零假设为假时才有意义。”
这两句话不等同——《效应大小解读指南》说对了。我认为您应该说的是“只有在不拒绝零假设时才能报告统计功效。”您可以这样想:当您拒绝零假设时,您报告 p 值,它为您提供了零假设被错误拒绝(如果它是真实的)的指示(即假阳性估计);而当您不拒绝零假设时,您报告功效,它为您提供了零假设被错误不拒绝(如果它是假的)的指示(即假阴性估计)。
请告知这是否合理?
感谢分享,听起来我需要仔细看看这一切。
已更新。
H0,零假设为假,意味着它被拒绝了。
我也同意 VSR 的观点。
我也同意,Jason。我认为您应该改回来。
我也同意。
谢谢你问这个问题,Phil。
很棒的文章,谢谢!
我的问题是——知道我正在运行的实验类型的典型标准差,我能否根据我的具体情况定制我的功效分析,以便更准确地了解我需要的样本量?目前看来,这似乎是一个一刀切的测试。
可能吧。我不太明白,抱歉。
标准差是效应大小的一部分。如果你知道你的人群之间的预期平均差值和标准差,你应该能够计算出你特定实验的效应大小。
来自 statsmodel 的文档
effect_size – 标准化效应大小,即两个均值之差除以标准差。effect_size 必须是正数。
精彩的博客。我喜欢阅读这篇文章,它给了我很大的信息。感谢您给我们提供如此有用的信息……!
不客气!
这太棒了,感谢您如此有条理,并提供了一个信息丰富的关于 Python 能力分析的解释,这非常有帮助!
谢谢,很高兴对您有帮助。
感谢您精彩的讲解。
我有一个关于此方法可能用例的问题。我收集了大量音乐人的歌曲,是通过 Spotify 进行某种名称匹配的。名称匹配并不完美,因此会影响我后续的分析。为了评估我的数据质量,我想随机抽取音乐人样本,手动为他们分配一个 Spotify ID,并检查我的名称匹配方法效果如何。所以,如果总共有 20000 名音乐人,最佳的随机样本量是多少?我能否以某种方式使用此处描述的方法?
也许可以参考不同样本量下某些度量的标准误差作为起点?
优秀的文章。解释得非常好。为理解这个令人困惑的主题奠定了基础。谢谢。
谢谢,很高兴能帮到你!
如果结果是二元的(1 和 0),并且我们试图比较两组,我们是不是不应该直接使用该软件包中的函数?谢谢!
抱歉,您确切地指什么?
抱歉,我没有说清楚,而且有一个错别字。我查阅了 statsmodels.stats.power 的文档。似乎到目前为止,如果我们想计算功效或样本量,我们就不能使用两样本比例检验(例如 R 中的 pwr.2p2n.test 或 pwr.2p.test)?我正在进行一项分析,其中结果是二元的。但我似乎没有在 Python 中找到与 pwr.2p2n.test 类似的函数。谢谢。
我明白了,我一时也不确定,抱歉。
你好,一旦我们知道了“效应大小”,我们该如何利用它呢?
我们可以使用效应大小来估计样本量。
我们可以使用样本量来估计效应大小,等等。
在运行实验之前,我们可以执行这些操作,以帮助确定我们想要看到的效应的大小以及我们可能需要的样本量。
这有帮助吗?
你好,谢谢你的回答。
嗯,我一直关注回归模型中变量前面的数字(无论是负数还是正数),来判断“一个变量对模型有什么影响”。
例如; y = 33 + 45 x1 + 35 x2 – 4 x3…
“x 前面的数字”
我可以举个例子吗?
假设我收集了两位网球运动员发球的数据……然后我用方差分析(ANOVA)比较他们的均值,看看他们
在统计学上是否存在显著差异。
在这种情况下,我有两个分布(两位网球运动员的发球),两个均值,我正在比较这两个分布/均值。
我的问题是……在这种情况下,查看 Cohen's d 和 Eta-squared,它们有什么用?在这种两位网球运动员的情况下,我为什么要去关注它们(Eta-squared、Cohen's d 效应大小)?
抱歉,我不明白。
你真是个英雄 <3
谢谢。
关于 Phil 两个月前的评论。较低的显著性水平会降低功效。如果功效 = 避免第二类错误的概率,那么我们应该降低未能拒绝零假设的几率。任何大于 alpha 的数字都意味着未能拒绝零假设。如果你增加 alpha,你就会增加功效。请进行更改,Phil 是错的……
感谢分享,Joshua。
谢谢 Jason。
正如您所知,许多机器学习模型本质上是高维的,有时有数千个特征为问题的解决方案提供信息。此外,算法通常比简单的统计检验(随机森林、支持向量机等)更复杂。是否有具体的指南或经验法则来降低高维预测或训练非传统统计检验算法的过拟合几率?
是的,有一个称为“正则化”的方法领域,旨在解决这个问题——小数据集和过拟合模型。
“…功效恰好是第二类错误的概率的倒数”—不应该是“第二类错误的概率的补集”而不是“第二类错误的概率的倒数”吗?
谢谢。
写得太好了。非常感谢!
谢谢!
一些来自读者的建议,也许可以讨论一下,在给定其他三个因素的情况下,如何计算样本量的公式?这比盲目复制/粘贴 Python 代码更容易让人理解。一篇展示这个想法的相当不错的文章可以在这里找到:https://towardsdatascience.com/understanding-power-analysis-in-ab-testing-14808e8a1554
不过这仍然是一篇很棒的文章,我喜欢阅读您关于统计主题的博客。
感谢您的建议。
这非常有用。我一直认为仅仅说 u1 != u2 是不够的。我们需要说明它们有多大差异。
您可能还需要查看效应大小。
https://machinelearning.org.cn/effect-size-measures-in-python/
我认为有一个错别字
功效 = 真阴性(当零假设为假时拒绝零假设)
第二类错误 = FN
功效 = 1-FN(第二类错误)
很棒的文章,信息量超大,谢谢!:)
不过有一个问题——我注意到在线计算器(例如 https://www.stat.ubc.ca/~rollin/stats/ssize/n2.html)在提供功效分析时需要 mu_1、mu_2 和标准差。而在您使用的 statsmodels 模块中(https://statsmodels.cn/stable/generated/statsmodels.stats.power.TTestIndPower.solve_power.html#statsmodels.stats.power.TTestIndPower.solve_power),对于功效只需要 3 个参数——alpha、effect_size 和 nobs1。这信息足够吗?我的意思是,我知道 effect_size 与 mu1、mu2 和 sd 相关(effect_size = (mu2-mu1)/sd),所以我想知道仅有 effect_size 是否足够,还是我们还需要均值和标准差?我尝试在纸上计算,但也许我在功效分析中的代数不够好:)
提前感谢您的回答 :) 我喜欢您所做的工作!
不客气。
我不确定第三方计算器,抱歉。
很棒的博客!不过有一个问题。当我们在使用 t 检验时,Cohen's d = 效应大小?它会大于 1 吗?
如果您查看定义,您会看到 Cohen's d = 均值差除以合并的标准差;因此,理论上它可以大于 1。
嗨,Jason,
您是否有关于两个组之间的“比率”如何改变计算的任何参考资料?
我在 statsmodels 文档中没有找到引用它们正在实现的公式的参考。
谢谢,
Josh
也许这个维基百科页面上的公式可以帮助解释:https://en.wikipedia.org/wiki/Paired_difference_test
请注意,公式中的两个总体的大小分别为 n_1 和 n_2;该库要求 n_1 和 n_1/n_2 的比率。
感谢您的文章。做得很好!
感谢您的反馈,Roberto!
嗨 Jason,感谢您非常实用的文章,
我有两个问题:第一个:当我们尝试在单个域上比较两个算法时,当我们使用 k-fold 或其他 CV 方法时,我们知道每个折叠的样本(例如,评估每个折叠的结果)不是独立的,我们应该使用 TTestIndPower 还是 TTestPower?
第二:当我们试图根据其他三个参数找到样本量的值时,这是我们需要比较两个算法的最小评估结果数(例如,k-fold T-times CV 方法中的 K 次 T),还是测试集应包含的样本数?
一如既往的优秀作品!
感谢您的反馈和支持 billy!我们非常感激!
你好——有人建议我可以使用功效分析来确定外部验证数据集的样本量,以评估我为大型数据集(5.5M 个观测值、3 个类别、1900 个特征)拟合的 XGBoost 模型的性能。这是功效分析的正确应用/用法吗?
嗨 Jas……您的理解是正确的!以下资源可能会让您更清楚
https://www.analyticsvidhya.com/blog/2020/12/statistics-for-beginners-power-of-power-analysis/
你好。首先,非常感谢您写得很好的文章(们)。
我有一个问题。我该如何事先计算效应大小?
对于非配对 t 检验,我想我应该使用对照组的均值与治疗组的均值(在实验之前),对吗?
但是,在配对 t 检验中,我该怎么做?因为现在我只有一个组,而且测试还没有进行。
谢谢!
嗨 Dimi……以下资源可能会让您感兴趣
https://machinelearning.org.cn/effect-size-measures-in-python/
“p 值与所选显著性水平的上下文有关。”
您是想写“插入”而不是“有关”吗?
“p > alpha:无法拒绝 H0,相同分布”
我认为这是不正确的。这个结果并不能让你得出样本来自同一总体的结论。它所能告诉你的是,如果样本确实来自同一总体,那么从该总体中随机选择样本观察值,得到这些样本统计量(均值、标准差)的概率是 p。
要得出样本来自同一总体的结论,我们需要一个概率分布,描述从不同总体中选择观察值会产生具有某些样本统计量的数据的概率。然后我们可以说,关于一组观察样本,从不同总体得出的概率(p)小于 alpha(例如 5%),从而肯定了零假设。
问题是我们没有这样的分布,所以我们永远无法得出零假设的结论。
感谢您的反馈,Norm!
你好,为什么“在这种情况下,我们可以将显著性水平视为在零假设为真时拒绝零假设的概率”是这样的?
嗨 Gill……以下资源希望能提供一些额外的见解
https://machinelearning.org.cn/statistical-hypothesis-tests/