机器学习中的统计容忍区间入门

作者 Jason Brownlee 于 2019年8月8日发布在统计学 20

为数据设置一个上限和下限是很有用的。

这些界限可以用来帮助识别异常值，并为预期结果设定范围。对来自一个总体的观测值设定的界限被称为容忍区间。容忍区间来自估计统计学领域。

容忍区间不同于量化单个预测值不确定性的预测区间。它也不同于量化总体参数（如均值）不确定性的置信区间。相反，容忍区间覆盖了总体分布的一个比例。

在本教程中，您将了解统计容忍区间以及如何为高斯数据计算容忍区间。

完成本教程后，您将了解：

统计容忍区间为来自总体的观测值提供了一个界限。
容忍区间需要同时指定覆盖比例和置信度。
对于具有高斯分布的数据样本，可以轻松计算其容忍区间。

通过我的新书《机器学习统计学》，快速启动您的项目，书中包含所有示例的分步教程和Python源代码文件。

让我们开始吧。

A Gentle Introduction to Statistical Tolerance Intervals in Machine Learning

机器学习中的统计容忍区间入门
照片由 Paul Hood 拍摄，保留部分权利。

教程概述

本教程分为4个部分，它们是：

数据界限
什么是统计容忍区间？
如何计算容忍区间
高斯分布的容忍区间

需要机器学习统计学方面的帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

数据界限

为数据设置界限很有用。

例如，如果您有一个来自某个领域的数据样本，了解正常值的上限和下限有助于识别数据中的异常或离群值。

对于正在进行预测的过程或模型，了解合理预测可能存在的预期范围是很有帮助的。

了解数据的常见取值范围有助于设定预期和检测异常。

数据的常见取值范围称为容忍区间。

什么是统计容忍区间？

容忍区间是基于对总体中数据比例的估计所设定的界限。

一个统计容忍区间 [包含] 来自抽样总体或过程的指定比例的单位。

— 第3页，《统计区间：从业者与研究者指南》，2017年。

该区间受抽样误差和总体分布方差的限制。根据大数定律，随着样本量的增加，概率将更好地匹配潜在的总体分布。

下面是一个陈述容忍区间的例子：

从x到y的范围以99%的置信度覆盖了95%的数据。

如果数据是高斯分布的，该区间可以用均值来表示；例如：

x +/- y 以99%的置信度覆盖了95%的数据。

我们称这些区间为统计容忍区间，以区别于工程学中描述可接受性限度的容忍区间，例如设计或材料的容忍度。通常，为方便起见，我们仅称之为“容忍区间”。

容忍区间由两个量定义：

覆盖率 (Coverage)：该区间所覆盖的总体比例。
置信度 (Confidence)：该区间覆盖了指定总体比例的概率性信心。

容忍区间是利用覆盖率和容忍系数这两个系数从数据中构建的。覆盖率是该区间应该包含的总体比例(p)。容忍系数是该区间达到指定覆盖率的置信度。一个覆盖率为95%、容忍系数为90%的容忍区间，将以90%的置信度包含95%的总体分布。

— 第175页，《环境工程师统计学》，第二版，2002年。

如何计算容忍区间

容忍区间的大小与来自总体的样本大小和总体的方差成正比。

根据数据的分布，计算容忍区间主要有两种方法：参数化方法和非参数化方法。

参数化容忍区间 (Parametric Tolerance Interval)：在指定覆盖率和置信度时，利用总体分布的知识。通常指高斯分布。
非参数化容忍区间 (Nonparametric Tolerance Interval)：使用秩统计量来估计覆盖率和置信度，由于缺少关于分布的信息，通常导致精度较低（区间更宽）。

对于从高斯分布中抽取的独立观测样本，容忍区间的计算相对直接。我们将在下一节演示这个计算过程。

高斯分布的容忍区间

在本节中，我们将通过一个例子来计算数据样本的容忍区间。

首先，让我们定义我们的数据样本。我们将创建一个包含100个观测值的样本，这些观测值从一个均值为50、标准差为5的高斯分布中抽取。

# generate dataset
data = 5 * randn(100) + 50

1 2	# 生成数据集 data = 5 * randn(100) + 50

在示例中，我们将假设我们不知道真实的总体均值和标准差，这些值必须被估计。

由于必须估计总体参数，因此存在额外的不确定性。例如，对于95%的覆盖率，我们可以使用距离估计均值1.96（或2）个标准差作为容忍区间。我们必须从样本中估计均值和标准差，并考虑到这种不确定性，因此区间的计算稍微复杂一些。

接下来，我们必须指定自由度。这将在计算临界值和计算区间时使用。具体来说，它用于计算标准差。

请记住，自由度是计算中可以变化的值的数量。这里，我们有100个观测值，因此有100个自由度。我们不知道标准差，因此必须使用均值来估计它。这意味着我们的自由度将是 (N – 1) 或 99。

# specify degrees of freedom
n = len(data)
dof = n - 1

# 指定自由度

n = len(data)

dof = n - 1

接下来，我们必须指定数据的覆盖比例。在这个例子中，我们关心的是中间95%的数据。比例是95。我们必须调整这个比例，使其覆盖中间的95%，即从第2.5个百分位数到第97.5个百分位数。

我们知道95%的临界值是1.96，因为我们经常使用它；尽管如此，我们可以在Python中根据逆生存函数的2.5%直接计算它。这可以使用SciPy的norm.isf()函数来计算。

# specify data coverage
prop = 0.95
prop_inv = (1.0 - prop) / 2.0
gauss_critical = norm.isf(prop_inv)

# 指定数据覆盖率

prop = 0.95

prop_inv = (1.0 - prop) / 2.0

gauss_critical = norm.isf(prop_inv)

接下来，我们需要计算覆盖率的置信度。我们可以通过从卡方分布中检索给定自由度和期望概率的临界值来做到这一点。我们可以使用SciPy的chi2.isf()函数。

# specify confidence
prob = 0.99
chi_critical = chi2.isf(q=prob, df=dof)

# 指定置信度

prob = 0.99

chi_critical = chi2.isf(q=prob, df=dof)

现在我们有了计算高斯容忍区间的所有要素。计算公式如下：

interval = sqrt((dof * (1 + (1/n)) * gauss_critical^2) / chi_critical)

1	interval = sqrt((dof * (1 + (1/n)) * gauss_critical^2) / chi_critical)

其中dof是自由度，n是数据样本的大小，gauss_critical是临界值，例如对于95%的总体覆盖率是1.96，而chi_critical是期望置信度和自由度下的卡方临界值。

interval = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)

1	interval = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)

我们可以将所有这些结合起来，为我们的数据样本计算高斯容忍区间。

完整的示例如下所示。

# parametric tolerance interval
from numpy.random import seed
from numpy.random import randn
from numpy import mean
from numpy import sqrt
from scipy.stats import chi2
from scipy.stats import norm
# seed the random number generator
seed(1)
# generate dataset
data = 5 * randn(100) + 50
# specify degrees of freedom
n = len(data)
dof = n - 1
# specify data coverage
prop = 0.95
prop_inv = (1.0 - prop) / 2.0
gauss_critical = norm.isf(prop_inv)
print('Gaussian critical value: %.3f (coverage=%d%%)' % (gauss_critical, prop*100))
# specify confidence
prob = 0.99
chi_critical = chi2.isf(q=prob, df=dof)
print('Chi-Squared critical value: %.3f (prob=%d%%, dof=%d)' % (chi_critical, prob*100, dof))
# tolerance
interval = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)
print('Tolerance Interval: %.3f' % interval)
# summarize
data_mean = mean(data)
lower, upper = data_mean-interval, data_mean+interval
print('%.2f to %.2f covers %d%% of data with a confidence of %d%%' % (lower, upper, prop*100, prob*100))

# 参数化容忍区间

from numpy.random import seed

from numpy.random import randn

from numpy import mean

from numpy import sqrt

from scipy.stats import chi2

from scipy.stats import norm

# 为随机数生成器设置种子

seed(1)

# 生成数据集

data = 5 * randn(100) + 50

# 指定自由度

n = len(data)

dof = n - 1

# 指定数据覆盖率

prop = 0.95

prop_inv = (1.0 - prop) / 2.0

gauss_critical = norm.isf(prop_inv)

print('高斯临界值: %.3f (覆盖率=%d%%)' % (gauss_critical, prop*100))

# 指定置信度

prob = 0.99

chi_critical = chi2.isf(q=prob, df=dof)

print('卡方临界值: %.3f (概率=%d%%, 自由度=%d)' % (chi_critical, prob*100, dof))

# 容忍度

interval = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)

print('容忍区间: %.3f' % interval)

# 总结

data_mean = mean(data)

lower, upper = data_mean-interval, data_mean+interval

print('%.2f 到 %.2f 覆盖了 %d%% 的数据，置信度为 %d%%' % (lower, upper, prop*100, prob*100))

运行该示例首先会计算并打印出高斯分布和卡方分布的相关临界值。然后打印出容忍度，并正确呈现出来。

Gaussian critical value: 1.960 (coverage=95%)
Chi-Squared critical value: 69.230 (prob=99%, dof=99)
Tolerance Interval: 2.355
47.95 to 52.66 covers 95% of data with a confidence of 99%

高斯临界值: 1.960 (覆盖率=95%)

卡方临界值: 69.230 (概率=99%, 自由度=99)

容忍区间: 2.355

47.95 到 52.66 覆盖了 95% 的数据，置信度为 99%

展示容忍区间如何随着样本量的增加而减小（变得更精确）也是很有帮助的。

下面的示例通过为同一个小的人为问题计算不同样本大小的容忍区间来证明这一点。

# plot tolerance interval vs sample size
from numpy.random import seed
from numpy.random import randn
from numpy import sqrt
from scipy.stats import chi2
from scipy.stats import norm
from matplotlib import pyplot
# seed the random number generator
seed(1)
# sample sizes
sizes = range(5,15)
for n in sizes:
	# generate dataset
	data = 5 * randn(n) + 50
	# calculate degrees of freedom
	dof = n - 1
	# specify data coverage
	prop = 0.95
	prop_inv = (1.0 - prop) / 2.0
	gauss_critical = norm.isf(prop_inv)
	# specify confidence
	prob = 0.99
	chi_critical = chi2.isf(q=prob, df=dof)
	# tolerance
	tol = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)
	# plot
	pyplot.errorbar(n, 50, yerr=tol, color='blue', fmt='o')
# plot results
pyplot.show()

# 绘制容忍区间与样本大小的关系图

from numpy.random import seed

from numpy.random import randn

from numpy import sqrt

from scipy.stats import chi2

from scipy.stats import norm

from matplotlib import pyplot

# 为随机数生成器设置种子

seed(1)

# 样本大小

sizes = range(5,15)

for n in sizes:

# 生成数据集

data = 5 * randn(n) + 50

# 计算自由度

dof = n - 1

# 指定数据覆盖率

prop = 0.95

prop_inv = (1.0 - prop) / 2.0

gauss_critical = norm.isf(prop_inv)

# 指定置信度

prob = 0.99

chi_critical = chi2.isf(q=prob, df=dof)

# 容忍度

tol = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)

# 绘图

pyplot.errorbar(n, 50, yerr=tol, color='blue', fmt='o')

# 绘制结果

pyplot.show()

运行此示例将创建一个图表，显示围绕真实总体均值的容忍区间。

我们可以看到，随着样本量从5增加到15个示例，区间变得更小（更精确）。

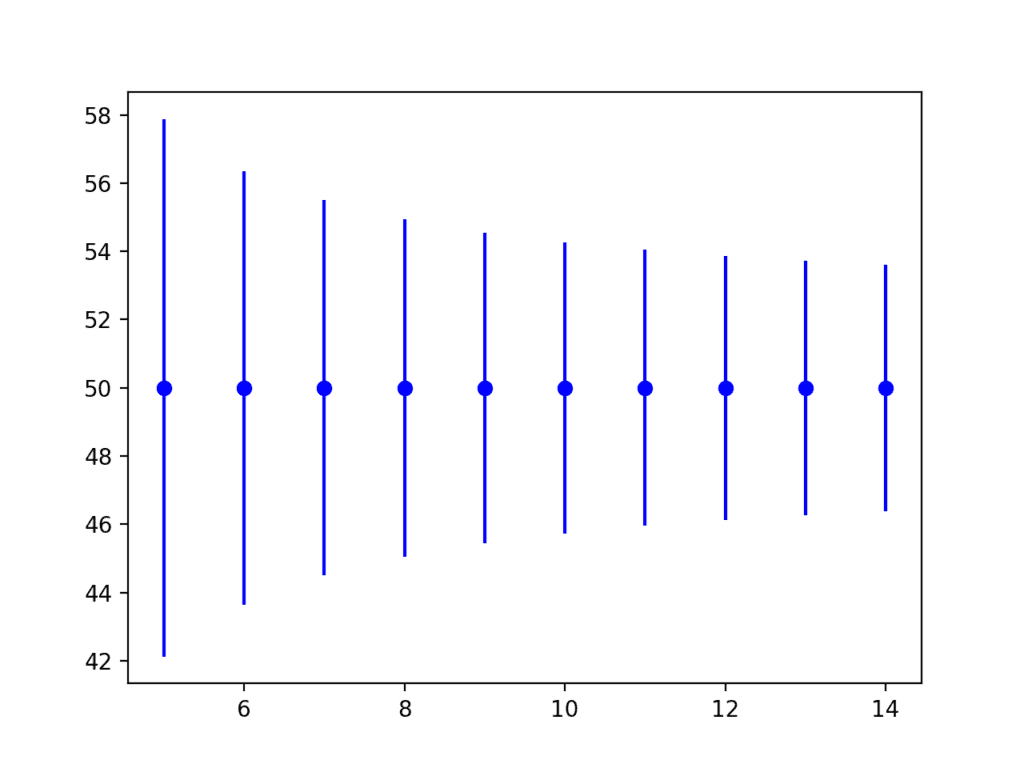
Error Bar Plot of Tolerance Interval vs Sample Size

容忍区间与样本大小的误差棒图

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

列出3个在机器学习项目中使用容忍区间的案例。
找到一个具有高斯变量的数据集，并为其计算容忍区间。
研究并描述一种计算非参数容忍区间的方法。

如果您探索了这些扩展中的任何一个，我很想知道。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

API

文章

总结

在本教程中，您了解了统计容忍区间以及如何为高斯数据计算容忍区间。

具体来说，你学到了：

统计容忍区间为来自总体的观测值提供了一个界限。
容忍区间需要同时指定覆盖比例和置信度。
对于具有高斯分布的数据样本，可以轻松计算其容忍区间。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

机器学习的预测区间

机器学习的估计统计学入门

对《机器学习中的统计容忍区间入门》的20条回应

Anthony The Koala 2018年6月3日晚上9:23 #

尊敬的Jason博士，
(1)
您能否告诉我第一个示例代码第25行中区间的公式来源？

interval = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)

1

interval = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)

(2) 与 (1) 相关的是输出

47.95 to 52.66 covers 95% of data with a confidence of 99%

1

47.95 到 52.66 覆盖了 95% 的数据，置信度为 a 99%

我的问题是
我理解均值 +- 2*标准差的置信区间的概念。也就是说，有95%的概率均值落在这些值之内。
我不理解的是“95%的数据，置信度为99%”这个输出。95%的数据具有99%的置信度是什么意思？

谢谢你，
悉尼的Anthony

回复
- Jason Brownlee 2018年6月4日早上6:27 #
  
  公式基于NIST手册
  https://www.itl.nist.gov/div898/handbook/prc/section2/prc263.htm
  
  如文章中所述，对于容忍区间，我们既有数据范围（覆盖率），也有该范围的可能性（置信度）。
  
  回复
  - Anthony The Koala 2018年6月4日下午1:40 #
    
    尊敬的Jason博士，
    谢谢您提供的参考资料。NIST网站似乎无法加载该页面，所以我去了archive.org网站：https://web.archive.org/web/20171202152145/https://www.itl.nist.gov/div898/handbook/prc/section2/prc263.htm。
    
    第25行的代码，
    
    tol = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)
    
    1
    
    tol = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)
    
    对应于页面上的k2公式。
    
    置信区间和容忍区间的区别在于“置信限是我们期望某个给定的总体参数（如均值）所在的范围。统计容忍限是我们期望规定比例的总体所在的范围。”——该网页的第二段。
    
    关键区别在于总体参数（如均值）内的限值和规定比例总体的限值。
    
    谢谢你，
    悉尼的Anthony
    
    回复
    - Jason Brownlee 2018年6月4日下午2:38 #
      
      同意。
      
      更多信息在这里
      https://machinelearning.org.cn/faq/single-faq/what-is-the-difference-between-tolerance-confidence-and-prediction-intervals
      
      回复
Kostas Theodor 2018年9月18日早上7:44 #

嗨，Jason，
在计算区间的公式中，是不是需要乘以样本标准差？
“容忍区间的大小与来自总体的样本大小成（反向？）比例，并与总体的方差成正比。”

回复
- Jason Brownlee 2018年9月18日下午2:16 #
  
  有很多方法可以计算区间。一种简单的参数化方法是使用标准差的一个因子。
  
  回复
  - James White 2019年1月9日凌晨4:38 #
    
    Jason，接着说——在您的代码示例中增加标准差对计算出的容忍限没有影响。这怎么可能呢？如果标准差增加了，那么容忍限肯定也必须增加。
    
    回复
    - Jason Brownlee 2019年1月9日早上8:50 #
      
      容忍区间不是置信区间或预测区间。
      
      回复
hao 2019年1月8日下午4:01 #

我不太明白。当我的样本均值为1和样本均值为1000时，没有区别。我得到相同的容忍区间。因为这里的代码除了最后一行，根本没有使用我样本的均值。所以，假设我想计算0.99的比例和0.95的置信度。对于相同数量的样本，我得到的容忍区间是3.355和102.355。

回复
- Jason Brownlee 2019年1月9日早上8:40 #
  
  容忍区间不是置信区间，关于置信区间的帮助请看这篇文章。
  https://machinelearning.org.cn/confidence-intervals-for-machine-learning/
  
  回复
KS Lam 2019年6月28日上午11:46 #

我计算的容忍区间是38.22到61.77，这与上面的值（即47.95到52.66）不同。我确定您的计算是错误的。

回复
- Jason Brownlee 2019年6月28日下午1:55 #
  
  也许API已经改变了？
  
  回复
  - KS Lam 2019年7月4日晚上7:39 #
    
    您最好修正这些错误，以便展示容忍区间的准确计算。谢谢。
    
    回复
    - Jason Brownlee 2019年7月5日早上7:55 #
      
      运行示例得到相同的结果，您具体认为哪个计算是错误的？
      
      您能确认您的库是最新的吗？
      
      回复
      - KS Lam 2019年7月6日下午5:19 #
        
        您可以使用在线容忍区间计算器来验证我上面提到的值。
        
        http://statpages.info/tolintvl.html
      - Jason Brownlee 2019年7月7日早上7:48 #
        
        感谢分享。
Alan Hibbing 2019年8月26日凌晨1:03 #

这个讨论话题正在解决如何使用容忍区间的问题——正是我试图解决的问题。文章指出，使用均值加减容忍区间来计算95%/99%的X轴限值。正如您在文章中所述：

“我们知道95%的临界值是1.96，因为我们经常使用它……”

当然，2.355与1.96相比听起来是正确的，但这个陈述中缺少了对1.96西格玛（sigma）的引用。

当我尝试使用均值周围1.96的范围时，我得到30.5%
=NORM.DIST(51.96,50,5,TRUE)-NORM.DIST(48.04,50,5,TRUE)

但当我将其改为1.96西格玛时，我确实得到了95%
=NORM.DIST(59.8,50,5,TRUE)-NORM.DIST(40.2,50,5,TRUE)

所以当我 sanity check 47.95到52.66的范围只有36.2%时，我并不感到惊讶
=NORM.DIST(52.66,50,5,TRUE)-NORM.DIST(47.95,50,5,TRUE)

有限的数据集其容忍限大于1.96西格玛是合理的，而这篇文章确实计算出容忍限为2.355。文章中令人困惑的陈述是：

“我们必须从样本中估计均值和标准差，并考虑到这种不确定性，因此区间的计算稍微复杂一些。
…
我们不知道标准差，因此必须使用均值来估计它。”

当然，任何可以估计均值的数据集也可以估计其标准差。假设标准差估计值接近生成数据的5.0西格玛，那么对于正态分布，2.355西格玛将是98.1%，这大于且应该大于期望的95%
=NORM.DIST(62.08,50,5,TRUE)-NORM.DIST(38.53,50,5,TRUE)

为了进一步确认在使用容忍限时缺少了这个西格玛，请检查

https://www.real-statistics.com/sampling-distributions/tolerance-interval/tolerance-interval-example/

回复
- Jason Brownlee 2019年8月26日早上6:19 #
  
  谢谢您的留言。
  
  是的，1.96西格玛，或者说z分数为1.96。
  
  回复
Vahid 2020年7月23日凌晨12:56 #

你好，
感谢这篇精彩的文章和源代码。我有点困惑。我猜别人也问过同样的问题，当我尝试使用这个实现和http://statpages.info/tolintvl.html上的界面时，结果与我从这个源代码得到的结果不同。大部分数字的计算方式是相同的，但在最后，不是

lower, upper = data_mean-interval, data_mean+interval

而是这样做
lower = data_mean- (interval * numpy.std(data))
upper也是一样。我想知道哪种方法是计算容忍区间的正确方法？

回复
- Jason Brownlee 2020年7月23日早上6:18 #
  
  它们是不同的，您描述的方法是将范围定义为标准差数量的函数
  https://en.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7_rule
  
  回复

导航

机器学习中的统计容忍区间入门

教程概述

需要机器学习统计学方面的帮助吗？

数据界限

什么是统计容忍区间？

如何计算容忍区间

高斯分布的容忍区间

扩展

进一步阅读

书籍

API

文章

总结

掌握机器学习统计学！

培养对统计学的实用理解

探索如何将数据转化为知识

关于此主题的更多信息

对《机器学习中的统计容忍区间入门》的20条回应

发表评论点击这里取消回复。

导航

教程概述

需要机器学习统计学方面的帮助吗？

数据界限

什么是统计容忍区间？

如何计算容忍区间

高斯分布的容忍区间

扩展

进一步阅读

书籍

API

文章

总结

掌握机器学习统计学！

培养对统计学的实用理解

探索如何将数据转化为知识

关于此主题的更多信息

对《机器学习中的统计容忍区间入门》的20条回应

发表评论 点击这里取消回复。

发表评论点击这里取消回复。