支持向量机（SVM）算法是最受欢迎的监督机器学习技术之一，并且在OpenCV库中得到了实现。
本教程将介绍在OpenCV中使用支持向量机所需的技能，我们将使用一个自定义数据集。在接下来的教程中，我们将把这些技能应用于图像分类和检测的具体场景。
在本教程中，您将学习如何将OpenCV的支持向量机算法应用于自定义的二维数据集。
完成本教程后，您将了解：
- 支持向量机的一些最重要的特征。
- 如何在OpenCV中使用支持向量机算法处理自定义数据集。
通过我的书《OpenCV 机器学习》启动您的项目。它提供了带有可用代码的自学教程。
让我们开始吧。
OpenCV 中的支持向量机
摄影：Lance Asper，部分权利保留。
教程概述
本教程分为两部分；它们是
- 回顾支持向量机的工作原理
- 探索OpenCV中的SVM算法
回顾支持向量机的工作原理
Jason Brownlee 在本教程中已经很好地解释了支持向量机（SVM）算法，但让我们先来回顾一下他教程中的一些要点。
- 为简单起见，假设我们有两个独立的类别，0 和 1。超平面可以分隔这两个类别中的数据点，决策边界将输入空间分割开以按类别分隔数据点。该超平面的维度取决于输入数据点的维度。
- 如果给出一个新观察到的数据点，我们可以通过计算它落在超平面的哪一侧来找出它所属的类别。
- “间隔”是决策边界与最近数据点之间的距离。它是通过仅考虑属于不同类别的最近数据点来找到的。它是通过计算这些最近数据点到决策边界的垂直距离来计算的。
- 与最近数据点之间的最大间隔是最佳决策边界的特征。这些最近的数据点被称为“支持向量”。
- 如果类别不能很好地相互分离，因为它们可能分布在空间中，导致一些数据点相互混合，那么最大化间隔的约束就需要放宽。可以通过引入一个称为“C”的可调参数来放宽间隔约束。
- C 参数的值控制着间隔约束可以被违反的程度，值为 0 意味着不允许任何违反。增加 C 值是为了在最大化间隔和减少错误分类数量之间取得更好的折衷。
- 此外，SVM 使用核函数来计算输入数据点之间的相似性（或距离）度量。在最简单的情况下，当输入数据是线性可分的，并且可以用线性超平面分隔时，核函数就实现了一个点积运算。
- 如果数据点不能直接线性分隔，那么“核技巧”就能派上用场，核函数执行的操作试图将数据转换到更高维度的空间，在该空间中数据变得线性可分。这类似于SVM在原始输入空间中寻找非线性决策边界。
探索OpenCV中的SVM算法
让我们首先考虑将SVM应用于一个简单的线性可分数据集，这将使我们能够可视化上述概念中的几个，然后再进行更复杂的任务。
为此，我们将生成一个包含 100 个数据点（由 `n_samples` 指定）的数据集，这些数据点等分为 2 个高斯簇（由 `centers` 指定），标准差设置为 1.5（由 `cluster_std` 指定）。为了能够复现结果，我们还需要定义 `random_state` 的值，我们将其设置为 15。
|
1 2 3 4 5 6 |
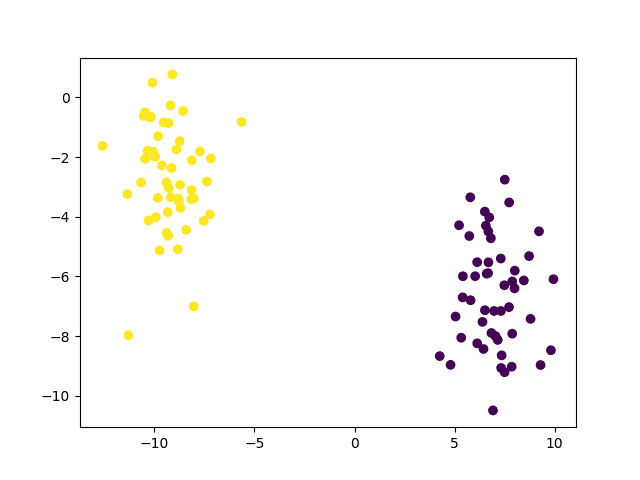
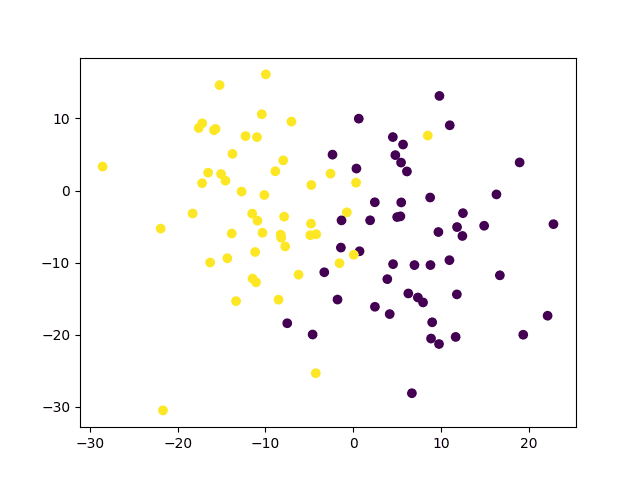
# 生成一个二维数据点及其真实标签的数据集 x, y_true = make_blobs(n_samples=100, centers=2, cluster_std=1.5, random_state=15) # 绘制数据集 scatter(x[:, 0], x[:, 1], c=y_true) show() |
上面的代码应该生成以下数据点图。您可能会注意到，我们将颜色值设置为真实标签，以便能够区分属于两个不同类别的数据点。
属于两个不同类别的线性可分数据点
下一步是将数据集分为训练集和测试集，前者将用于训练SVM，后者将用于测试。
|
1 2 3 4 5 6 7 8 9 10 |
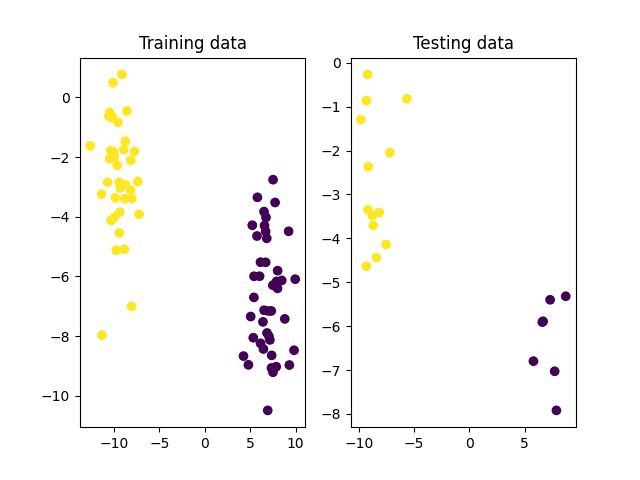
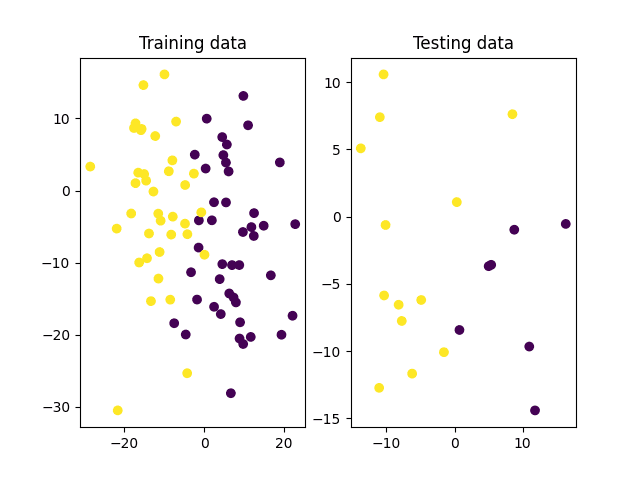
# 将数据拆分为训练集和测试集 x_train, x_test, y_train, y_test = ms.train_test_split(x, y_true, test_size=0.2, random_state=10) # 绘制训练集和测试集 fig, (ax1, ax2) = subplots(1, 2) ax1.scatter(x_train[:, 0], x_train[:, 1], c=y_train) ax1.set_title('训练数据') ax2.scatter(x_test[:, 0], x_test[:, 1], c=y_test) ax2.set_title('测试数据') show() |
将数据点分为训练集和测试集
从上面的训练数据图中可以看出，两个类别非常容易区分，应该能被一个线性超平面轻松分隔。因此，让我们继续在OpenCV中创建和训练一个使用线性核来找到这两个类别之间最佳决策边界的SVM。
|
1 2 3 4 5 6 7 8 |
# 创建一个新的SVM svm = ml.SVM_create() # 将SVM核设置为线性 svm.setKernel(ml.SVM_LINEAR) # 在训练数据集合上训练SVM svm.train(x_train.astype(float32), ml.ROW_SAMPLE, y_train) |
这里需要注意的是，OpenCV中的SVM的`train`方法要求输入数据为32位浮点类型。
我们可以继续使用训练好的SVM来预测测试数据的标签，并随后通过比较预测结果与其对应的真实标签来计算分类器的准确率。
|
1 2 3 4 5 6 |
# 预测测试数据的目标标签 _, y_pred = svm.predict(x_test.astype(float32)) # 计算并打印获得的准确度 accuracy = (sum(y_pred[:, 0].astype(int) == y_test) / y_test.size) * 100 print('准确率:', accuracy, ‘%') |
|
1 |
准确率：100.0 % |
正如预期的那样，所有的测试数据点都得到了正确分类。让我们也可视化SVM算法在训练期间计算出的决策边界，以便更好地理解它是如何得出此分类结果的。
在此期间，到目前为止的代码列表如下：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
from sklearn.datasets import make_blobs from sklearn import model_selection as ms from numpy import float32 from matplotlib.pyplot import scatter, show, subplots # 生成一个二维数据点及其真实标签的数据集 x, y_true = make_blobs(n_samples=100, centers=2, cluster_std=1.5, random_state=15) # 绘制数据集 scatter(x[:, 0], x[:, 1], c=y_true) show() # 将数据拆分为训练集和测试集 x_train, x_test, y_train, y_test = ms.train_test_split(x, y_true, test_size=0.2, random_state=10) # 绘制训练集和测试集 fig, (ax1, ax2) = subplots(1, 2) ax1.scatter(x_train[:, 0], x_train[:, 1], c=y_train) ax1.set_title('训练数据') ax2.scatter(x_test[:, 0], x_test[:, 1], c=y_test) ax2.set_title('测试数据') show() # 创建一个新的SVM svm = ml.SVM_create() # 将SVM核设置为线性 svm.setKernel(ml.SVM_LINEAR) # 在训练数据集合上训练SVM svm.train(x_train.astype(float32), ml.ROW_SAMPLE, y_train) # 预测测试数据的目标标签 _, y_pred = svm.predict(x_test.astype(float32)) # 计算并打印获得的准确度 accuracy = (sum(y_pred[:, 0].astype(int) == y_test) / y_test.size) * 100 print('准确率:', accuracy, '%') |
为了可视化决策边界，我们将创建许多二维点，并将它们组织成一个矩形网格，该网格跨越用于测试的数据点所占据的空间。
|
1 2 |
x_bound, y_bound = meshgrid(arange(x_test[:, 0].min() - 1, x_test[:, 0].max() + 1, 0.05), arange(x_test[:, 1].min() - 1, x_test[:, 1].max() + 1, 0.05)) |
接下来，我们将把构成矩形网格的数据点的 x 和 y 坐标组织成一个两列的数组，并将它们传递给 `predict` 方法，为每个点生成一个类别标签。
|
1 2 |
bound_points = column_stack((x_bound.reshape(-1, 1), y_bound.reshape(-1, 1))).astype(float32) _, bound_pred = svm.predict(bound_points) |
最后，我们可以通过一个等高线图叠加测试数据点来可视化它们，以确认SVM算法计算出的决策边界确实是线性的。
|
1 2 3 |
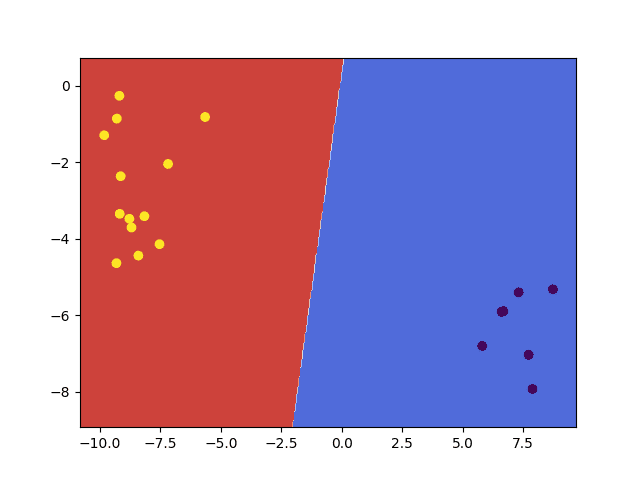
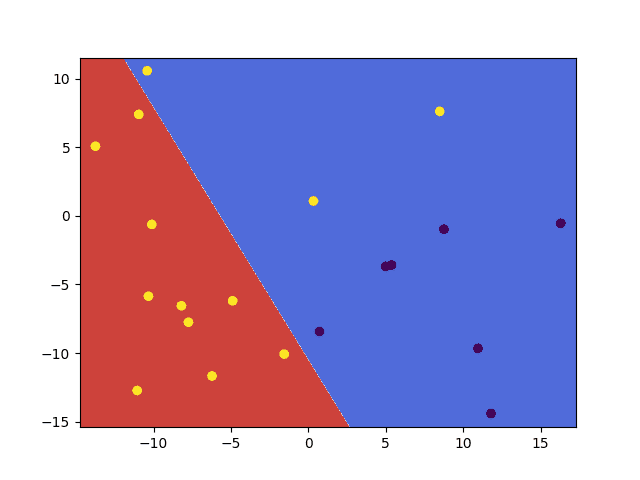
contourf(x_bound, y_bound, bound_pred.reshape(x_bound.shape), cmap=cm.coolwarm) scatter(x_test[:, 0], x_test[:, 1], c=y_test) show() |
SVM计算的线性决策边界
从上图也可以证实，正如在第一部分中所提到的，测试数据点被分配的类别标签取决于它们位于决策边界的哪一侧。
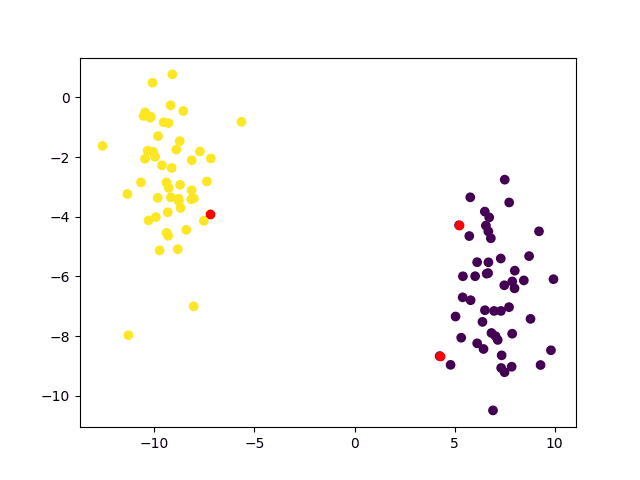
此外，我们可以高亮显示被识别为支持向量的训练数据点，这些点在确定决策边界方面起着关键作用。
|
1 2 3 4 5 |
support_vect = svm.getUncompressedSupportVectors() scatter(x[:, 0], x[:, 1], c=y_true) scatter(support_vect[:, 0], support_vect[:, 1], c='red') show() |
红色高亮显示的支持向量
生成决策边界并可视化支持向量的完整代码列表如下：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
from numpy import float32, meshgrid, arange, column_stack from matplotlib.pyplot import scatter, show, contourf, cm x_bound, y_bound = meshgrid(arange(x_test[:, 0].min() - 1, x_test[:, 0].max() + 1, 0.05), arange(x_test[:, 1].min() - 1, x_test[:, 1].max() + 1, 0.05)) bound_points = column_stack((x_bound.reshape(-1, 1), y_bound.reshape(-1, 1))).astype(float32) _, bound_pred = svm.predict(bound_points) # 绘制测试集 contourf(x_bound, y_bound, bound_pred.reshape(x_bound.shape), cmap=cm.coolwarm) scatter(x_test[:, 0], x_test[:, 1], c=y_test) show() support_vect = svm.getUncompressedSupportVectors() scatter(x[:, 0], x[:, 1], c=y_true) scatter(support_vect[:, 0], support_vect[:, 1], c='red') show() |
到目前为止，我们已经考虑了具有两个清晰可区分类别中最简单的情况。但是，当我们区分那些由于数据点相互混合而在空间中重叠不那么清晰的类别时，该怎么办？例如以下情况：
|
1 2 |
# 生成一个二维数据点及其真实标签的数据集 x, y_true = make_blobs(n_samples=100, centers=2, cluster_std=8, random_state=15) |
不线性可分数据点属于两个不同的类别
将非线性可分数据分为训练集和测试集
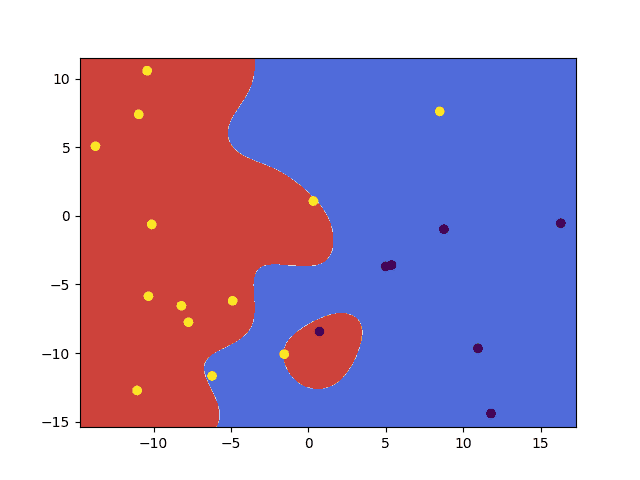
在这种情况下，我们可能需要根据两个类别重叠的程度来探索不同的选项，例如（1）通过增加 C 参数的值来放宽线性核的间隔约束，以在最大化间隔和减少错误分类之间取得更好的折衷；或者（2）使用不同的核函数，例如径向基函数（RBF），它可以产生非线性决策边界。
为此，我们需要设置 SVM 和所用核函数的几个属性值。
- SVM_C_SVC：称为“C-支持向量分类”，此 SVM 类型允许对不完全分离（即非线性可分）的类别进行 n 类分类（n $\geq$ 2）。使用 `setType` 方法设置。
- C：在处理非线性可分类别时，离群值的惩罚乘数。使用 `setC` 方法设置。
- Gamma：确定 RBF 核函数的半径。较小的 gamma 值会产生一个更宽的半径，可以捕捉远离彼此的数据点之间的相似性，但这可能导致过拟合。较大的 gamma 值会产生一个更窄的半径，只能捕捉附近数据点之间的相似性，这可能导致欠拟合。使用 `setGamma` 方法设置。
这里，C 和 gamma 值是任意设置的，但您可以进行进一步测试以研究不同值如何影响所得的预测准确率。使用以下代码，上述两种选项都能提供 85% 的预测准确率，但通过不同的决策边界实现。
- 使用具有放宽间隔约束的线性核
|
1 2 3 |
svm.setKernel(ml.SVM_LINEAR) svm.setType(ml.SVM_C_SVC) svm.setC(10) |
使用具有放宽间隔约束的线性核计算的决策边界
- 使用 RBF 核函数
|
1 2 3 4 |
svm.setKernel(ml.SVM_RBF) svm.setType(ml.SVM_C_SVC) svm.setC(10) svm.setGamma(0.1) |
使用 RBF 核计算的决策边界
SVM 参数值的选择通常取决于具体任务和现有数据，需要通过进一步测试来相应地进行调整。
进一步阅读
如果您想深入了解此主题，本节提供了更多资源。
书籍
- OpenCV 机器学习, 2017.
- 使用 Python 精通 OpenCV 4, 2019.
网站
总结
在本教程中，您学习了如何将OpenCV的支持向量机算法应用于自定义的二维数据集。
具体来说，你学到了：
- 支持向量机算法的一些最重要的特征。
- 如何在OpenCV中使用支持向量机算法处理自定义数据集。
你有什么问题吗？
在下面的评论中提出您的问题，我将尽力回答。
开始使用 OpenCV 进行机器学习！
学习如何在图像处理项目中使用机器学习技术
...以高级方式使用 OpenCV，超越像素处理
在我的新电子书中探索如何实现
OpenCV 机器学习
它提供带有所有可用 Python 代码的自学教程，让您从新手成长为专家。它为您提供了
逻辑回归、随机森林、支持向量机、k 均值聚类、神经网络等等……所有这些都使用 OpenCV 中的机器学习模块
暂无评论。