测试时增强,简称 TTA,是一种提高预测模型技能的技术。
它通常用于提高深度学习模型在图像数据集上的预测性能,通过对测试数据集中每个图像的多个增强版本进行预测取平均值。
虽然 TTA 在图像数据集和神经网络模型上很流行,但它可以用于任何机器学习算法的表格数据集,例如回归和分类预测建模问题中常见的那些。
在本教程中,您将了解如何使用 scikit-learn 中的表格数据进行测试时增强。
完成本教程后,您将了解:
- 测试时增强是一种提高模型性能的技术,常用于深度学习模型在图像数据集上的应用。
- 如何使用 Python 的 scikit-learn 实现回归和分类表格数据集的测试时增强。
- 如何调整测试时增强中使用的合成示例的数量和统计噪声的量。
开始您的项目,阅读我的新书《机器学习数据准备》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。

Scikit-Learn 实现测试时增强
照片由 barnimages 提供,部分权利保留。
教程概述
本教程分为三个部分;它们是:
- 测试时增强
- 标准模型评估
- 测试时增强示例
测试时增强
测试时增强,简称 TTA,是一种提高预测模型技能的技术。
这是一种在拟合模型进行预测时(例如在测试数据集或新数据上)实现的流程。该流程涉及创建数据集中每个示例的多个轻微修改版本。对每个修改后的示例进行预测,然后对预测值进行平均,以获得对原始示例的更准确的预测。
TTA 常用于图像分类,其中使用图像数据增强来创建每个图像的多个修改版本,例如裁剪、缩放、旋转和其他图像特定修改。因此,该技术可以提升图像分类算法在标准数据集上的性能。
在其 2015 年发表的、在 ILSVRC 数据集上取得了当时最先进结果的论文《大规模图像识别的深度卷积网络》中,作者使用了水平翻转测试时增强。
我们还通过图像的水平翻转来增强测试集;将原始图像和翻转图像的 softmax 类后验概率进行平均,以获得图像的最终分数。
— Very Deep Convolutional Networks for Large-Scale Image Recognition,2015。
有关图像数据的测试时增强的更多信息,请参阅教程
虽然 TTA 常用于图像数据,但它也可以用于其他数据类型,例如表格数据(例如数字的行和列)。
TTA 有多种方法可用于表格数据。一种简单的方法包括创建带有少量高斯噪声的行数据副本。然后可以对复制行的预测值进行平均,从而提高回归或分类的预测性能。
我们将探讨如何使用 scikit-learn Python 机器学习库来实现这一点。
首先,让我们定义一种标准的模型评估方法。
想开始学习数据准备吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
标准模型评估
在本节中,我们将探讨在下一节介绍测试时增强之前,评估机器学习模型的典型方法。
首先,让我们定义一个合成分类数据集。
我们将使用 make_classification() 函数 创建一个包含 100 个示例的数据集,每个示例有 20 个输入变量。
该示例创建并总结了数据集。
|
1 2 3 4 5 6 |
# 测试分类数据集 from sklearn.datasets import make_classification # 定义数据集 X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # 汇总数据集 print(X.shape, y.shape) |
运行示例创建数据集并确认数据集的行数和列数。
|
1 |
(100, 20) (100,) |
这是一个二分类任务,我们将拟合和评估一个线性模型,具体来说,是一个逻辑回归模型。
评估机器学习模型的一个好习惯是使用重复的 k 折交叉验证。当数据集是分类问题时,重要的是确保使用分层的 k 折交叉验证版本。因此,我们将使用重复分层 k 折交叉验证,包含 10 折和 5 次重复。
|
1 2 3 |
... # 准备交叉验证过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=5, random_state=1) |
我们将手动枚举折和重复,以便稍后执行测试时增强。
在每个循环中,我们必须定义并拟合模型,然后使用拟合的模型进行预测,评估预测,并存储结果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
... scores = list() for train_ix, test_ix in cv.split(X, y): # split the data X_train, X_test = X[train_ix], X[test_ix] y_train, y_test = y[train_ix], y[test_ix] # 拟合模型 model = LogisticRegression() model.fit(X_train, y_train) # 评估模型 y_hat = model.predict(X_test) acc = accuracy_score(y_test, y_hat) scores.append(acc) |
最后,我们可以报告所有折和重复的平均分类准确率。
|
1 2 3 |
... # 报告表现 print('Accuracy: %.3f (%.3f)' % (mean(scores), std(scores))) |
将这些内容整合起来,下面列出了在合成二分类数据集上评估逻辑回归模型的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 使用重复分层 k 折交叉验证评估逻辑回归 from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score # 创建数据集 X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # 准备交叉验证过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=5, random_state=1) scores = list() for train_ix, test_ix in cv.split(X, y): # split the data X_train, X_test = X[train_ix], X[test_ix] y_train, y_test = y[train_ix], y[test_ix] # 拟合模型 model = LogisticRegression() model.fit(X_train, y_train) # 评估模型 y_hat = model.predict(X_test) acc = accuracy_score(y_test, y_hat) scores.append(acc) # 报告表现 print('Accuracy: %.3f (%.3f)' % (mean(scores), std(scores))) |
运行示例将使用重复分层 k 折交叉验证评估逻辑回归。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到模型达到了 79.8% 的平均分类准确率。
|
1 |
Accuracy: 0.798 (0.110) |
接下来,让我们探讨如何更新此示例以使用测试时增强。
测试时增强示例
实现测试时增强涉及两个步骤。
第一步是选择一种创建测试集每行修改版本的方法。
在本教程中,我们将为每个特征添加高斯随机噪声。另一种方法可以是添加均匀随机噪声,甚至复制测试数据集中的示例特征值。
将使用 NumPy 的 normal() 函数来创建具有零均值和小型标准差的随机高斯值向量。标准差应与训练数据集中每个变量的分布成比例。在此情况下,我们将使示例保持简单,并使用 0.02 的值。
|
1 2 3 4 5 |
... # 创建高斯随机向量 gauss = normal(loc=0.0, scale=feature_scale, size=len(row)) # 添加到测试用例 new_row = row + gauss |
给定测试集中的一行数据,我们可以创建给定数量的修改副本。建议使用奇数个副本,例如 3、5 或 7,因为当我们之后对每个副本分配的标签进行平均时,我们希望自动打破平局。
下面的 `create_test_set()` 函数实现了这一点;给定一行数据,它将返回一个测试集,其中包含该行以及 “n_cases” 个修改后的副本,默认为 3(因此测试集大小为 4)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 为具有未知标签的真实数据行创建测试集 def create_test_set(row, n_cases=3, feature_scale=0.2): test_set = list() test_set.append(row) # make copies of row for _ in range(n_cases): # create vector of random gaussians gauss = normal(loc=0.0, scale=feature_scale, size=len(row)) # add to test case new_row = row + gauss # store in test set test_set.append(new_row) return test_set |
对该方法的一个改进是,在每个循环中对训练集和测试集进行标准化或归一化,然后使用与标准正态分布有意义的特征一致的标准差来调用 normal()。这留给读者作为练习。
第二个设置是为测试集中的每个示例使用 `create_test_set()`,为构建的测试集进行预测,并通过汇总统计量(跨预测值)记录预测标签。鉴于预测是分类的,统计众数是合适的,通过 scipy 的 mode() 函数。如果数据集是回归的,或者我们在预测概率,那么均值或中位数将更合适。
|
1 2 3 4 5 6 7 |
... # 创建测试集 test_set = create_test_set(row) # 为测试集中的所有示例进行预测 labels = model.predict(test_set) # 选择预测标签作为分布的众数 label, _ = mode(labels) |
下面的 `test_time_augmentation()` 函数实现了这一点;给定一个模型和一个测试集,它返回一个预测数组,其中每个预测都是通过测试时增强生成的。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 使用测试时增强进行预测 def test_time_augmentation(model, X_test): # 评估模型 y_hat = list() for i in range(X_test.shape[0]): # retrieve the row row = X_test[i] # create the test set test_set = create_test_set(row) # make a prediction for all examples in the test set labels = model.predict(test_set) # select the label as the mode of the distribution label, _ = mode(labels) # store the prediction y_hat.append(label) return y_hat |
将所有这些内容整合在一起,下面列出了使用测试时增强在数据集上评估逻辑回归模型的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
# 使用测试时增强评估逻辑回归 from numpy.random import seed from numpy.random import normal from numpy import mean from numpy import std from scipy.stats import mode from sklearn.datasets import make_classification from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score # 为具有未知标签的真实数据行创建测试集 def create_test_set(row, n_cases=3, feature_scale=0.2): test_set = list() test_set.append(row) # make copies of row for _ in range(n_cases): # create vector of random gaussians gauss = normal(loc=0.0, scale=feature_scale, size=len(row)) # add to test case new_row = row + gauss # store in test set test_set.append(new_row) return test_set # 使用测试时增强进行预测 def test_time_augmentation(model, X_test): # 评估模型 y_hat = list() for i in range(X_test.shape[0]): # retrieve the row row = X_test[i] # create the test set test_set = create_test_set(row) # make a prediction for all examples in the test set labels = model.predict(test_set) # select the label as the mode of the distribution label, _ = mode(labels) # store the prediction y_hat.append(label) return y_hat # 初始化 NumPy 随机数生成器 seed(1) # 创建数据集 X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # 准备交叉验证过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=5, random_state=1) scores = list() for train_ix, test_ix in cv.split(X, y): # split the data X_train, X_test = X[train_ix], X[test_ix] y_train, y_test = y[train_ix], y[test_ix] # 拟合模型 model = LogisticRegression() model.fit(X_train, y_train) # make predictions using test-time augmentation y_hat = test_time_augmentation(model, X_test) # calculate the accuracy for this iteration acc = accuracy_score(y_test, y_hat) # 存储结果 scores.append(acc) # 报告表现 print('Accuracy: %.3f (%.3f)' % (mean(scores), std(scores))) |
运行示例将使用重复分层 k 折交叉验证和测试时增强来评估逻辑回归。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到模型达到了 81.0% 的平均分类准确率,这比不使用测试时增强的测试框架(准确率为 79.8%)要好。
|
1 |
Accuracy: 0.810 (0.114) |
对测试时增强期间创建的合成示例数量进行网格搜索可能很有趣。
下面的示例探讨了 1 到 20 之间的值,并绘制了结果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
# 比较测试时增强期间创建的合成示例数量 from numpy.random import seed from numpy.random import normal from numpy import mean from numpy import std from scipy.stats import mode from sklearn.datasets import make_classification from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score from matplotlib import pyplot # 为具有未知标签的真实数据行创建测试集 def create_test_set(row, n_cases=3, feature_scale=0.2): test_set = list() test_set.append(row) # make copies of row for _ in range(n_cases): # create vector of random gaussians gauss = normal(loc=0.0, scale=feature_scale, size=len(row)) # add to test case new_row = row + gauss # store in test set test_set.append(new_row) return test_set # 使用测试时增强进行预测 def test_time_augmentation(model, X_test, cases): # 评估模型 y_hat = list() for i in range(X_test.shape[0]): # retrieve the row row = X_test[i] # create the test set test_set = create_test_set(row, n_cases=cases) # make a prediction for all examples in the test set labels = model.predict(test_set) # select the label as the mode of the distribution label, _ = mode(labels) # store the prediction y_hat.append(label) return y_hat # 评估测试时创建的不同数量的合成示例 examples = range(1, 21) results = list() for e in examples: # initialize numpy random number generator seed(1) # 创建数据集 X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # prepare the cross-validation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=5, random_state=1) scores = list() for train_ix, test_ix in cv.split(X, y): # split the data X_train, X_test = X[train_ix], X[test_ix] y_train, y_test = y[train_ix], y[test_ix] # 拟合模型 model = LogisticRegression() model.fit(X_train, y_train) # make predictions using test-time augmentation y_hat = test_time_augmentation(model, X_test, e) # calculate the accuracy for this iteration acc = accuracy_score(y_test, y_hat) # 存储结果 scores.append(acc) # 报告性能 print('>%d, acc: %.3f (%.3f)' % (e, mean(scores), std(scores))) results.append(mean(scores)) # 绘制结果图 pyplot.plot(examples, results) pyplot.show() |
运行示例将报告在测试时增强期间创建的不同数量的合成示例的准确率。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。考虑运行示例几次并比较平均结果。
回想一下,我们在上一个示例中使用了三个示例。
在这种情况下,对于这个测试框架来说,3 个示例似乎是最佳选择,因为所有其他值似乎都会导致性能下降。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
>1, acc: 0.800 (0.118) >2, acc: 0.806 (0.114) >3, acc: 0.810 (0.114) >4, acc: 0.798 (0.105) >5, acc: 0.802 (0.109) >6, acc: 0.798 (0.107) >7, acc: 0.800 (0.111) >8, acc: 0.802 (0.110) >9, acc: 0.806 (0.105) >10, acc: 0.802 (0.110) >11, acc: 0.798 (0.112) >12, acc: 0.806 (0.110) >13, acc: 0.802 (0.110) >14, acc: 0.802 (0.109) >15, acc: 0.798 (0.110) >16, acc: 0.796 (0.111) >17, acc: 0.806 (0.112) >18, acc: 0.796 (0.111) >19, acc: 0.800 (0.113) >20, acc: 0.804 (0.109) |
绘制了示例数量与分类准确率的折线图,表明奇数个示例通常比偶数个示例产生更好的性能。
这可能是因为在使用预测众数时,它们能够打破平局。
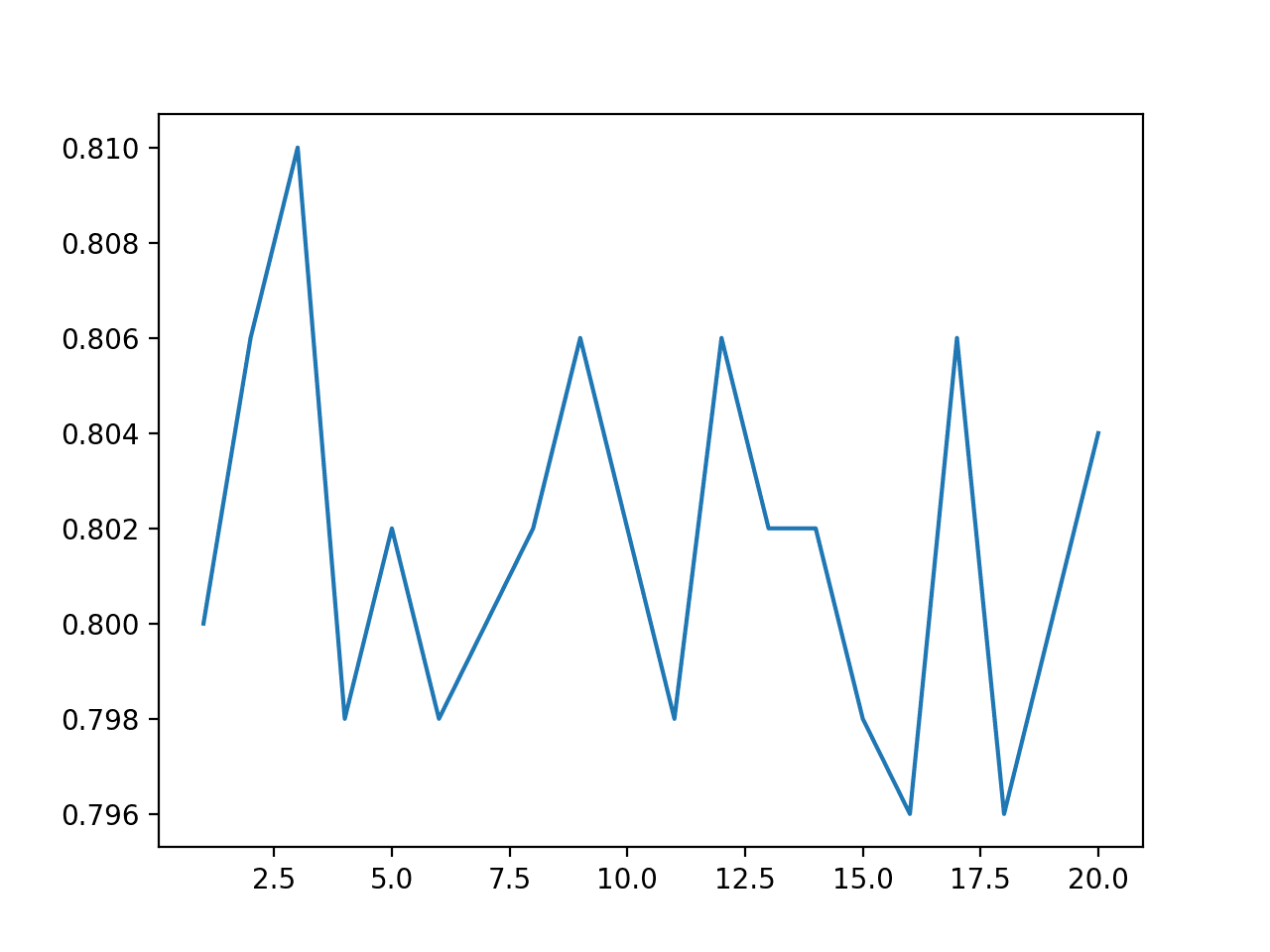
TTA 中的合成示例数量与分类准确率的折线图
我们还可以对在测试时增强期间添加到测试集示例中的随机噪声量进行相同的敏感性分析。
下面的示例演示了这一点,噪声值在 0.01 到 0.3 之间,步长为 0.01。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
# 比较测试时增强期间创建的示例中添加的噪声量 from numpy.random import seed from numpy.random import normal from numpy import arange from numpy import mean from numpy import std from scipy.stats import mode from sklearn.datasets import make_classification from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score from matplotlib import pyplot # 为具有未知标签的真实数据行创建测试集 def create_test_set(row, n_cases=3, feature_scale=0.2): test_set = list() test_set.append(row) # make copies of row for _ in range(n_cases): # create vector of random gaussians gauss = normal(loc=0.0, scale=feature_scale, size=len(row)) # add to test case new_row = row + gauss # store in test set test_set.append(new_row) return test_set # 使用测试时增强进行预测 def test_time_augmentation(model, X_test, noise): # 评估模型 y_hat = list() for i in range(X_test.shape[0]): # retrieve the row row = X_test[i] # create the test set test_set = create_test_set(row, feature_scale=noise) # make a prediction for all examples in the test set labels = model.predict(test_set) # select the label as the mode of the distribution label, _ = mode(labels) # store the prediction y_hat.append(label) return y_hat # 评估测试时创建的不同数量的合成示例 noise = arange(0.01, 0.31, 0.01) results = list() for n in noise: # initialize numpy random number generator seed(1) # 创建数据集 X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # prepare the cross-validation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=5, random_state=1) scores = list() for train_ix, test_ix in cv.split(X, y): # split the data X_train, X_test = X[train_ix], X[test_ix] y_train, y_test = y[train_ix], y[test_ix] # 拟合模型 model = LogisticRegression() model.fit(X_train, y_train) # make predictions using test-time augmentation y_hat = test_time_augmentation(model, X_test, n) # calculate the accuracy for this iteration acc = accuracy_score(y_test, y_hat) # 存储结果 scores.append(acc) # 报告性能 print('>noise=%.3f, acc: %.3f (%.3f)' % (n, mean(scores), std(scores))) results.append(mean(scores)) # 绘制结果图 pyplot.plot(noise, results) pyplot.show() |
运行示例将报告在测试时增强期间创建的示例中添加的不同数量的统计噪声的准确率。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。考虑运行示例几次并比较平均结果。
回想一下,我们在第一个示例中使用了 0.02 的标准差。
在这种情况下,对于这个测试框架来说,大约 0.230 的值似乎是最佳的,从而获得了略高的 81.2% 的准确率。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
>noise=0.010, acc: 0.798 (0.110) >noise=0.020, acc: 0.798 (0.110) >noise=0.030, acc: 0.798 (0.110) >noise=0.040, acc: 0.800 (0.113) >noise=0.050, acc: 0.802 (0.112) >noise=0.060, acc: 0.804 (0.111) >noise=0.070, acc: 0.806 (0.108) >noise=0.080, acc: 0.806 (0.108) >noise=0.090, acc: 0.806 (0.108) >noise=0.100, acc: 0.806 (0.108) >noise=0.110, acc: 0.806 (0.108) >noise=0.120, acc: 0.806 (0.108) >noise=0.130, acc: 0.806 (0.108) >noise=0.140, acc: 0.806 (0.108) >noise=0.150, acc: 0.808 (0.111) >noise=0.160, acc: 0.808 (0.111) >noise=0.170, acc: 0.808 (0.111) >noise=0.180, acc: 0.810 (0.114) >noise=0.190, acc: 0.810 (0.114) >noise=0.200, acc: 0.810 (0.114) >噪声=0.210, 准确率: 0.810 (0.114) >噪声=0.220, 准确率: 0.810 (0.114) >噪声=0.230, 准确率: 0.812 (0.114) >噪声=0.240, 准确率: 0.812 (0.114) >噪声=0.250, 准确率: 0.812 (0.114) >噪声=0.260, 准确率: 0.812 (0.114) >噪声=0.270, 准确率: 0.810 (0.114) >噪声=0.280, 准确率: 0.808 (0.116) >噪声=0.290, 准确率: 0.808 (0.116) >噪声=0.300, 准确率: 0.808 (0.116) |
创建了一个线图,展示了添加到示例中的噪声量与分类准确率的关系,表明在标准差为0.250左右的小范围内噪声可能在此测试平台上是最佳的。
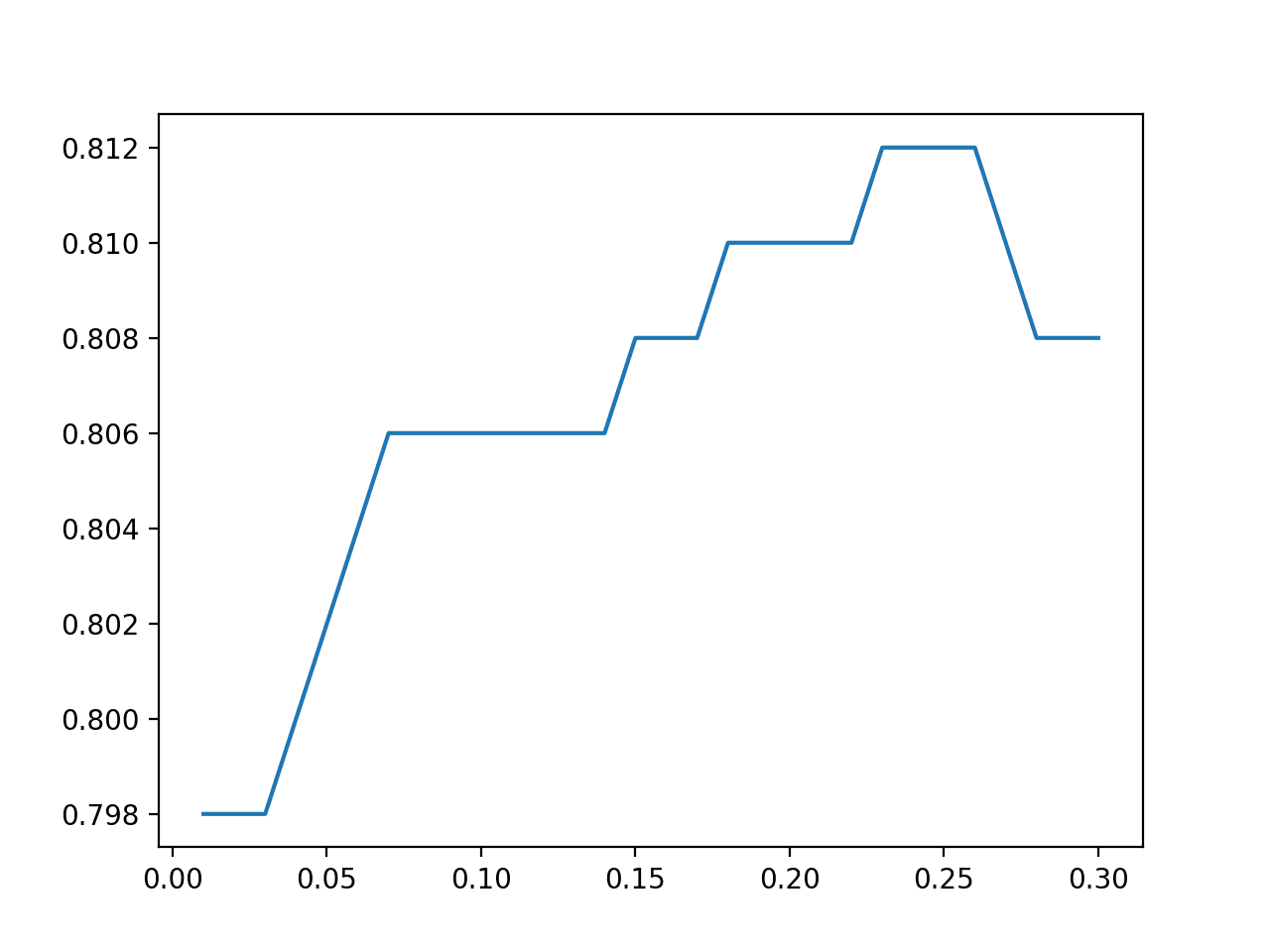
TTA中添加到示例中的统计噪声与分类准确率的线图
为什么不使用 SMOTE 这样的过采样方法?
SMOTE 是一种流行的过采样方法,用于重新平衡训练数据集中每个类的观测值。它可以创建合成样本,但需要了解类标签,这使得它不易用于测试时增强。
一种方法可能是获取一个需要预测的给定示例,并假设它属于某个给定的类。然后,使用新示例作为合成的焦点,从训练数据集中生成合成样本,并对它们进行分类。然后对每个类标签重复此操作。可以统计每个类别组的总分类响应(可能是概率)或平均分类响应,并将响应最大的组作为预测。
这只是我的初步想法,我还没有真正尝试过这种方法。您不妨试试,如果有效请告诉我。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
API
- sklearn.datasets.make_classification API.
- sklearn.model_selection.RepeatedStratifiedKFold API.
- numpy.random.normal API.
- scipy.stats.mode API.
总结
在本教程中,您学习了如何在 scikit-learn 中为表格数据使用测试时增强。
具体来说,你学到了:
- 测试时增强是一种提高模型性能的技术,常用于深度学习模型在图像数据集上的应用。
- 如何使用 Python 的 scikit-learn 实现回归和分类表格数据集的测试时增强。
- 如何调整测试时增强中使用的合成示例的数量和统计噪声的量。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






先生,我们是否在优化技术之后应用测试时增强?例如,在深度学习的超参数优化之后?
是的,它与已拟合的模型一起使用。而不是在训练期间。
先生,测试时增强是否与深度学习模型一起使用?
可以,这里有一个图像数据的示例
https://machinelearning.org.cn/how-to-use-test-time-augmentation-to-improve-model-performance-for-image-classification/
先生,您有关于测试时增强的论文吗?
抱歉,我没有。
先生,请提供表格数据上使用深度学习的测试时增强。
感谢您的建议。
您可以直接将上述示例改编用于深度学习模型。
我理解测试时增强,但我需要了解如何在其他研究中应用增强中的过采样。
你具体指的是什么?
我有一篇关于乳腺癌的论文,作者应用了增强。我不知道作者是如何应用于数据集的。
也许可以通过电子邮件联系作者并询问?
将图像特定技术应用于数值数据集非常有帮助。
是否可以将增强应用于单类数值训练数据集以生成另一类,然后将机器学习算法应用于具有两类的测试数据集?
也许可以,试试看——制作原型并看看。
没有电子邮件联系方式
也许通过谷歌搜索作者。
好的,谢谢
杰森博士,
在“标准模型评估”部分,我想计算循环的迭代次数
当我设置 RepeatedStratifiedIKFold 的 n_splits 和 n_repeats 时。
设置 n_splits=10, n_repeats=5
循环有 50 次迭代
将参数更改为 n_splits=100, n_repeats=5
有 500 次迭代。
用于复制的代码
为什么 count = n_iterations * n_repeat?
我以为循环计算的是重复的次数。
.
谢谢你,
悉尼的Anthony
如果有 10 个折叠和 5 次重复,那么我们期望有折叠 * 重复或 500 次迭代,从而得到结果。
尊敬的Jason博士,
谢谢回复。我明白了为什么迭代次数是 no_of_folds * repeats。
转述一下
我们有一个数据集。我们将数据集分成 k 折。也就是说,我们从数据集中抽取 k 个随机样本。对于每一折,我们将数据集分成训练样本和测试样本。训练样本用于训练模型,测试样本用于测试模型。
“重复”意味着将 k 折重复“重复”次。
因此,总迭代次数为 no_of_folds * repeats。
来源:副标题 K-Fold 交叉验证是什么?,https://medium.com/datadriveninvestor/k-fold-cross-validation-6b8518070833。
您自己也许会问,“……什么是 train_ix 和 test_ix?”
答案:train_ix 是从 train_X 和 train_y 集合的选取中得到的索引数组。同样,test_ix 是从 test_X 和 test_y 集合的选取中得到的索引数组。
谢谢你,
悉尼的Anthony
感谢您在表格数据 TTA 方面的帮助。非常非常有用。我期待在工作和 Kaggle 上应用它!
不客气,请让我知道您的进展!
恭喜,你很棒
谢谢!
Jason,这个技术是否包含在您关于数据准备的书籍中?
不,它对于这本书来说有点太专业了。
你好 Jason,我有一个类别不平衡问题。 SMOTE 在训练数据上对我有用。由于不平衡方法的正确进行训练-测试分割方法是使用分层方法,我的测试数据也不平衡。
我读了这篇文章的最后一段。如果我分别对训练数据和测试数据进行 SMOTE,这是否是增强测试数据的正确方法?这可以确保训练数据的信息不会泄露到测试数据中。所以我认为这是正确的。您能否分享您的想法?
不应该将 SMOTE 应用于测试数据集。它只能应用于训练数据集。
你好 Jason,如果您能解释原因,我将不胜感激,因为它将帮助我理解。
不应对完整数据集应用 SMOTE,因为这会在训练期间泄露测试数据信息。我完全同意这一点。
但是,正如我上面提到的,SMOTE 是在分割 **之后** 分别应用于训练和测试数据的。我需要理解为什么不能这样做。
此外,我想在此补充一点,我正在为训练集和测试集使用不同的 SMOTE 技术,因为目标是纯粹地根据其自身数据特性来增强测试集,从而让算法有机会尝试预测更多测试样本。
粘贴代码
oversample_train = ADASYN(sampling_strategy = ‘all’, random_state = 0)
X_train, y_train = oversample_train.fit_resample(X_train, y_train)
oversample_test = SMOTE(sampling_strategy = ‘all’, random_state = 0)
X_test, y_test = oversample_test.fit_resample(X_test, y_test)
使用 SMOTE 改变训练集会使模型的训练产生偏差——这是好事——它表现得更好。
测试集旨在评估模型在训练期间未使用的数据上的性能。如果更改了测试集,例如更改了分布,那么对该测试集上的任何模型的评估都是无效的。
切勿将 SMOTE 应用于测试集。
谢谢 Jason!
非常感谢您出色的帖子。
在您的示例中,所有特征都是数值特征。如果训练集和测试集中存在一些分类特征,如何使用测试时增强方法?该方法是否也适用于回归问题?
不客气。
我认为该方法不适用于分类输入,除非它们具有序数关系——在这种情况下,您可以使用多项式概率分布来采样它们的取值,也许。或者干脆不重采样分类输入。
是的,我怀疑您可以将此方法用于回归。
非常感谢您出色的帖子。
我能否将此技术应用于完全数值型数据集?
你为什么认为你不能?
为了我的项目工作,我想使用数据增强过程。我已经使用了变分自动编码器方法。如果我能使用它,我可以比较两种方法。
此外,我的输出不是分类。