
Python 中的聚类入门指南
作者 | Ideogram 提供图片
聚类是一种在许多领域广泛应用的方法,例如客户和图像分割、图像识别、生物信息学以及异常检测,所有这些都是为了根据相似性将数据分组到簇中。聚类方法具有双重性质:作为一种旨在发现无标签数据(无监督学习)潜在知识的机器学习技术,以及作为一种用于揭示数据隐藏模式的描述性数据分析工具。
本文将介绍如何在 Python 中使用常见的聚类方法,即 k-means 聚类和层次聚类。
基本原理与实践考量
实施聚类方法需要考虑几个问题。
数据集的大小和维度
数据集的大小和其中包含的特征数量不仅会影响聚类性能和质量,还会影响查找聚类的计算效率。对于高维数据,请考虑使用降维方法(如 PCA),这可以提高聚类准确性并减少噪声。大型数据集可能需要基于本文将要演示的基本方法但带有更多复杂性的高级优化方法。
要查找的簇的数量
这是一个关键但往往并非易事的问题。您拥有一个拥有数千名客户的大型客户群,并希望将他们细分为具有相似购物行为的客户群?您可能根本不知道要预先查找的细分数量。像肘部法则、轮廓分析或甚至是人类专家的领域知识这样的成熟方法可以帮助您做出这个关键决定。簇太少可能无法得出有意义的区分,而簇太多可能导致模型过拟合或对未来数据缺乏泛化能力。
聚类的指导标准
选择合适的相似性度量对于查找有意义的簇至关重要。欧氏距离在紧凑的球状簇上表现良好,但对于更不规则的结构,像余弦相似性或曼哈顿距离这样的其他度量可能是更明智的选择。聚类算法(例如 k-means、层次聚类、DBSCAN 等)的选择必须与数据的分布和问题的需求相匹配。
现在来看两个 Python 中聚类的实际示例。
实例 1:k-means 聚类
第一个示例展示了 **k-means** 的一个简单应用,用于根据两个特征:年收入和消费金额对购物中心的客户数据集进行细分。您可以在此处 完整查看数据集及其特征。
像往常一样,Python 中的一切都始于导入必要的包和数据
|
1 2 3 4 5 6 7 |
import pandas as pd import matplotlib.pyplot as plt from sklearn.cluster import KMeans from sklearn.preprocessing import StandardScaler url = "https://raw.githubusercontent.com/gakudo-ai/open-datasets/refs/heads/main/Mall_Customers.csv" df = pd.read_csv(url) |
我们现在选择所需的特征,它们位于第四列和第五列。此外,对数据进行标准化通常有助于找到更高质量的簇,尤其是在特征之间的值范围变化很大的情况下。
|
1 2 3 4 |
X = df.iloc[:, [3, 4]].values scaler = StandardScaler() X_scaled = scaler.fit_transform(X) |
我们现在使用导入的 KMeans 来使用 Scikit-learn 库的 k-means 实现。重要的是,k-means 是一种迭代聚类方法,它要求预先指定簇的数量。假设一位营销和零售专家提前告诉我们,尝试在数据中查找五个子群可能是有意义的。然后我们按如下方式应用 k-means。
|
1 2 3 |
# k=5 个簇的 K-means kmeans = KMeans(n_clusters=5, random_state=42, n_init=10) df['Cluster'] = kmeans.fit_predict(X_scaled) |
请注意,我们如何向数据集中添加了一个名为“Cluster”的新特征,其中包含每个客户所属的簇的标识符。这将在稍后非常方便,用于使用不同的颜色绘制簇并可视化结果。
|
1 2 3 4 5 6 |
# 绘制簇 plt.scatter(X[:, 0], X[:, 1], c=df['Cluster'], cmap='viridis', edgecolors='k') plt.xlabel('年收入') plt.ylabel('消费评分') plt.title('K-Means 聚类') plt.show() |
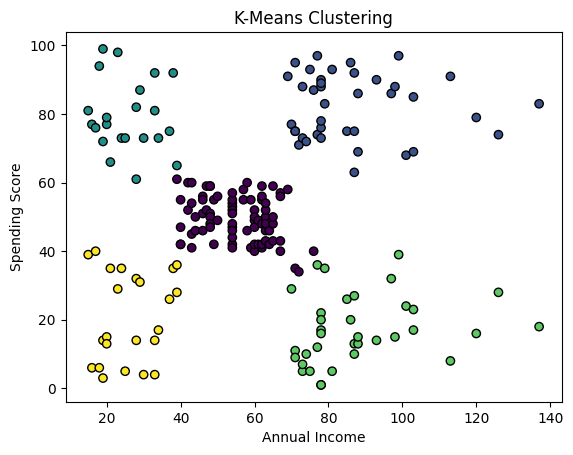
看起来我们专家的直觉非常正确!如果您不确定,可以使用肘部法则并尝试不同的簇数设置来找到最有希望的设置。 本文解释了如何在同一数据集和场景中执行此操作。
实例 2:层次聚类
与 k-means 不同,**层次聚类**方法不严格要求预先指定簇的数量,而是创建一个称为树状图的层次结构,从而可以灵活地选择簇。让我们看看如何做到。
|
1 2 |
import scipy.cluster.hierarchy as sch from sklearn.cluster import AgglomerativeClustering |
在应用凝聚聚类之前,我们绘制之前处理和缩放过的数据集的树状图:这可能有助于我们确定最佳簇数量(让我们暂时假装我们忘记了专家之前告诉我们的事情)。
|
1 2 3 4 5 6 |
plt.figure(figsize=(8, 5)) dendrogram = sch.dendrogram(sch.linkage(X_scaled, method='ward')) plt.title('树状图') plt.xlabel('客户') plt.ylabel('欧氏距离') plt.show() |
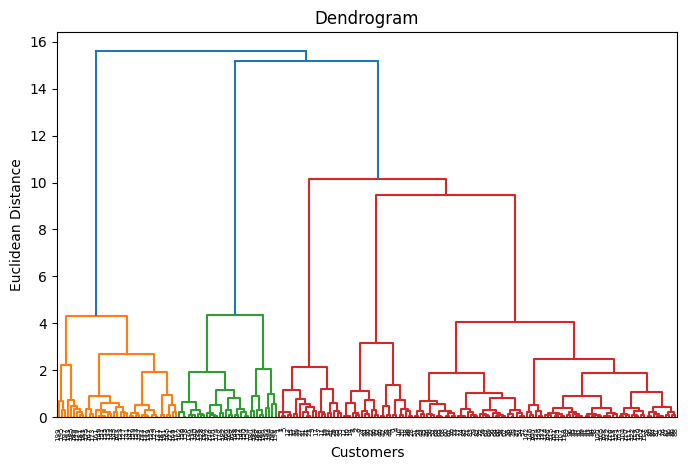
同样,k=5 听起来是个不错的簇数。原因是,如果您画一条横跨树状图的水平线,在某些点上,被切割的垂直分支既不太远也不太集中,您将在树状图被水平切割五次的高度处这样做。
以下是我们应用层次聚类算法并可视化结果的方法。
|
1 2 3 4 5 6 7 8 |
hc = AgglomerativeClustering(n_clusters=5, affinity='euclidean', linkage='ward') df['Cluster_HC'] = hc.fit_predict(X_scaled) plt.scatter(X[:, 0], X[:, 1], c=df['Cluster_HC'], cmap='plasma', edgecolors='k') plt.xlabel('年收入') plt.ylabel('消费评分') plt.title('层次聚类') plt.show() |
除了所需的簇数量外,我们还指定了亲和力或相似性度量,即**欧氏**距离,以及链接策略,它决定了簇之间的距离如何计算:在我们的例子中,我们选择了 **ward** 链接,它最小化了合并簇内的方差,以实现更紧凑的 agrupamiento。
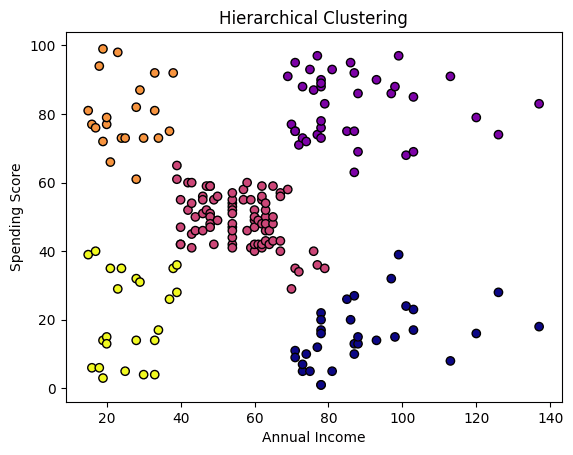
这些结果与 k-means 的结果非常相似,只是在簇边界的点上有一些细微的差异。
干得好!





暂无评论。