优化作为许多机器学习算法中的核心过程之一,依赖于导数的使用,以决定如何更新模型的参数值,以最大化或最小化目标函数。
本教程将继续探索查找函数导数的不同技术。特别是,我们将探讨幂法则、乘积法则和商法则,它们可以帮助我们比从第一原理推导每个导数更快地得出函数导数。因此,对于特别具有挑战性的函数,掌握这些法则来求导变得越来越重要。
在本教程中,您将学习如何使用幂法则、乘积法则和商法则来求函数的导数。
完成本教程后,您将了解:
- 在求变量基数(幂为固定值)的导数时,应遵循幂法则。
- 乘积法则如何使我们能够求出定义为另外两个(或更多)函数乘积的函数的导数。
- 商法则如何使我们能够求出定义为两个可微分函数之比的函数的导数。
让我们开始吧。

幂法则、乘积法则和商法则
图片来源 Andreas M,部分权利保留。
教程概述
本教程分为三个部分;它们是:
- 幂法则
- 乘积法则
- 商法则
幂法则
如果一个变量基数有固定幂,求导数的规则是把幂移到变量基数前面,然后将幂减1。
例如,如果函数为 f(x) = x2,我们想求它的导数,我们首先把 2 移到 x 前面,然后将幂减 1
f(x) = x2
f’(x) = 2x
为了更好地理解这个法则的来源,让我们采取更长的方法,从导数的定义开始求 f(x) 的导数
在这里,我们用 f(x) = x2 进行替换,然后简化表达式
当 h 趋近于 0 时,这个极限趋近于 2x,这与我们之前使用幂法则得到的结果一致。
如果应用于 f(x) = x,幂法则会给出 1 的值。这是因为,当我们将 1 移到 x 前面,然后将幂减 1 后,指数位置剩下 0。由于 x0 = 1,所以 f’(x) = (1) (x0) = 1。
理解这个导数的最好方法是意识到 f(x) = x 是一条符合 y = mx + b 形式的直线,因为 f(x) = x 等同于 f(x) = 1x + 0(或 y = 1x + 0)。这条直线的斜率(m)是 1,所以导数等于 1。或者你可以直接记住 x 的导数是 1。但如果你忘记了这两种方法,你总是可以使用幂法则。
《傻瓜微积分》第131页,2016年。
幂法则可以应用于任何幂,无论是正数、负数还是分数。我们也可以通过先将它们的指数(或幂)表示为分数,来将其应用于根式函数
f(x) = √x = x1/2
f’(x) = (1 / 2) x-1/2
乘积法则
假设我们现在有一个函数 f(x),我们想求它的导数,它是另外两个函数 u(x) = 2x2 和 v(x) = x3 的乘积
f(x) = u(x) v(x) = (2x2) (x3)
为了探究如何求 f(x) 的导数,我们首先直接求 u(x) 和 v(x) 乘积的导数
(u(x) v(x))’ = ((2x2) (x3))’ = (2x5)’ = 10x4
现在让我们来研究一下,如果我们先分别计算这两个函数的导数,然后再将它们相乘,会发生什么情况。
u’(x) v’(x) = (2x2)’ (x3)’ = (4x) (3x2) = 12x3
显然,第二个结果与第一个不符,这是因为我们没有应用乘积法则。
乘积法则告诉我们,两个函数乘积的导数可以这样求得
f’(x) = u’(x) v(x) + u(x) v’(x)
我们可以通过应用极限的性质,从导数的定义开始,推导出乘积法则。
我们知道 f(x) = u(x) v(x),因此我们可以代入 f(x) 和 f(x + h)
在这个阶段,我们的目标是将分子分解成几个可以单独计算的极限。为此,将引入项 u(x) v(x + h) – u(x) v(x + h) 到分子中。它的引入并不会改变我们刚刚得到的 f’(x) 的定义,但它将帮助我们分解分子
结果表达式看起来很复杂,但是仔细观察我们会发现有可以提取的公因式
通过应用极限法则,我们可以将和与积分解成单独的极限,从而进一步简化表达式。
我们问题的解决方案现在变得更加清晰。我们可以看到,简化表达式中的第一项和最后一项分别对应于 u(x) 和 v(x) 的导数定义,我们可以分别表示为 u(x)’ 和 v(x)’。第二项在 h 趋近于 0 时趋近于连续可微分函数 v(x),而第三项是 u(x)。
因此,我们再次得出乘积法则
f’(x) = u’(x) v(x) + u(x) v’(x)
有了这个新工具,让我们重新考虑当 u(x) = 2x2 和 v(x) = x3 时如何求 f’(x)
f’(x) = u’(x) v(x) + u(x) v’(x)
f’(x) = (4x) (x3) + (2x2) (3x2) = 4x4 + 6x4 = 10x4
得到的导数现在与我们之前得到的乘积的导数 (u(x) v(x))’ 正确匹配。
这是一个相当简单的例子,我们原本可以直接计算。但是,我们可能会遇到更复杂的问题,涉及不能直接相乘的函数,此时我们可以轻松应用乘积法则。例如
f(x) = x2 sin x
f’(x) = (x2)’ (sin x) + (x2) (sin x)’ = 2x sin x + x2 cos x
我们甚至可以将乘积法则扩展到两个以上的函数。例如,假设 f(x) 现在定义为三个函数 u(x)、v(x) 和 w(x) 的乘积
f(x) = u(x) v(x) w(x)
我们可以按如下方式应用乘积法则
f’(x) = u’(x) v(x) w(x) + u(x) v’(x) w(x) + u(x) v(x) w’(x)
商法则
类似地,商法则告诉我们如何求一个函数 f(x) 的导数,该函数是两个可微分函数 u(x) 和 v(x) 的比值。
我们可以像对乘积法则一样,从第一原理推导出商法则,即从导数的定义开始,并应用极限的性质。或者我们可以走捷径,直接使用乘积法则推导出商法则。这次我们选择这条路线。
我们可以对 u(x) 应用乘积法则,得到
u’(x) = f’(x) v(x) + f(x) v’(x)
反解 f’(x) 得到
最后一步代入 f(x) 即可得出商法则
我们已经看到了如何求 正弦和余弦函数的导数。现在使用商法则,我们也可以求出正切函数的导数。
f(x) = tan x = sin x / cos x
应用商法则并简化结果表达式
根据三角学中的勾股恒等式,我们知道 cos2x + sin2x = 1,因此
因此,利用商法则,我们很容易得出正切的导数是平方正割函数。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 微积分傻瓜书, 2016.
文章
总结
在本教程中,您学习了如何应用幂法则、乘积法则和商法则来求函数的导数。
具体来说,你学到了:
- 在求变量基数(幂为固定值)的导数时,应遵循幂法则。
- 乘积法则如何使我们能够求出定义为另外两个(或更多)函数乘积的函数的导数。
- 商法则如何使我们能够求出定义为两个可微分函数之比的函数的导数。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。
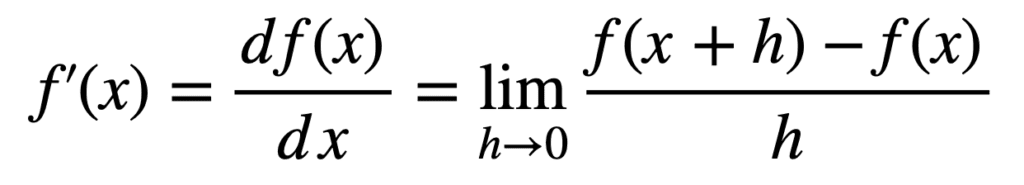
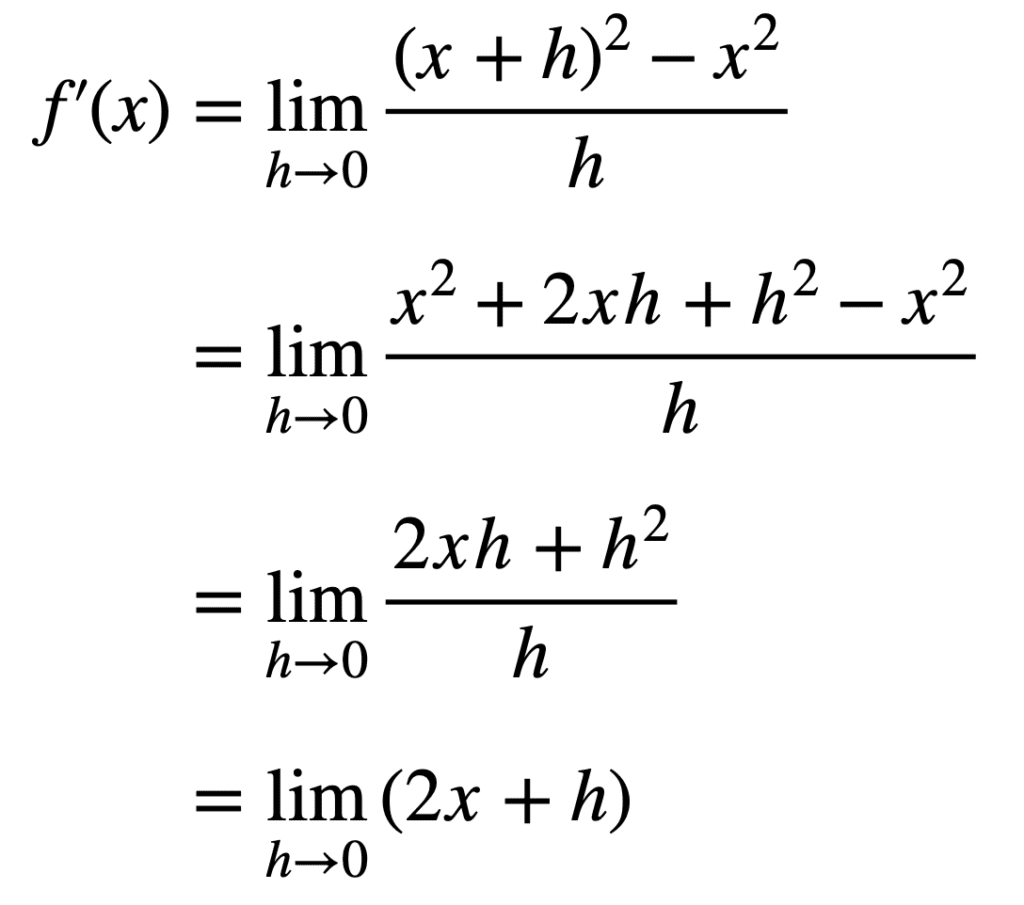
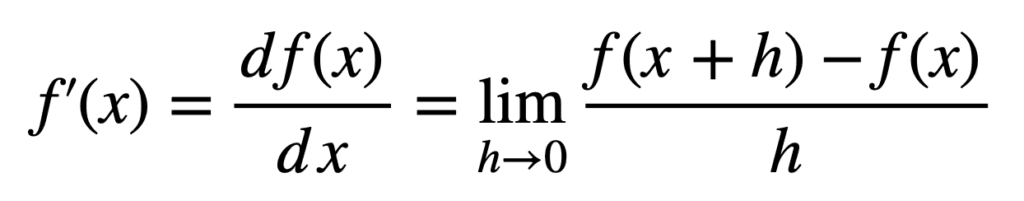
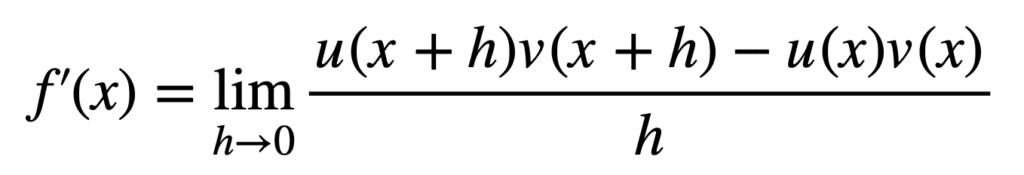
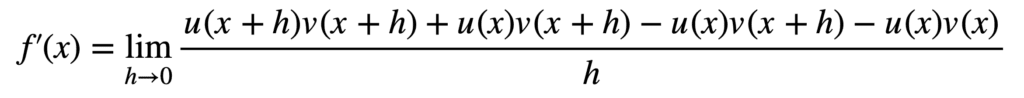
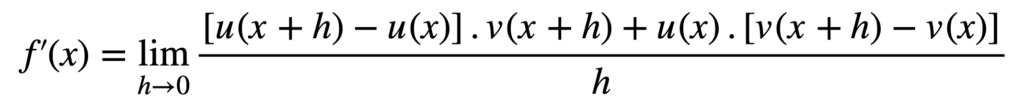
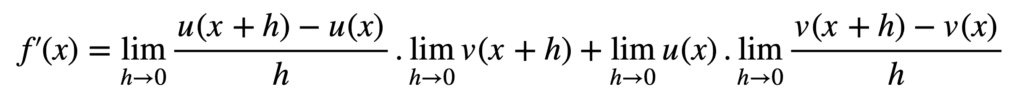
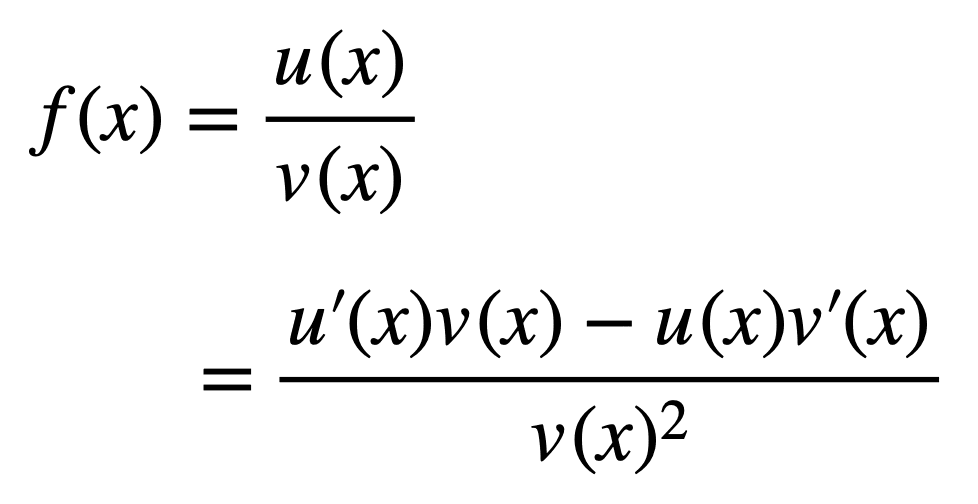

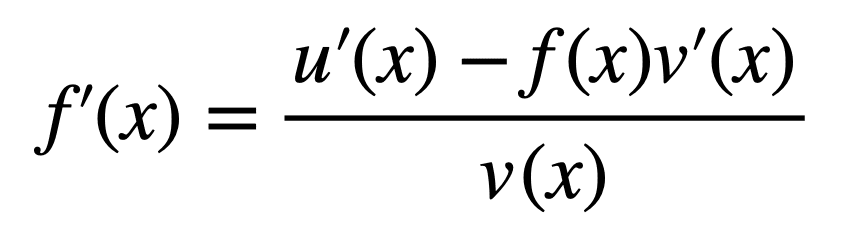
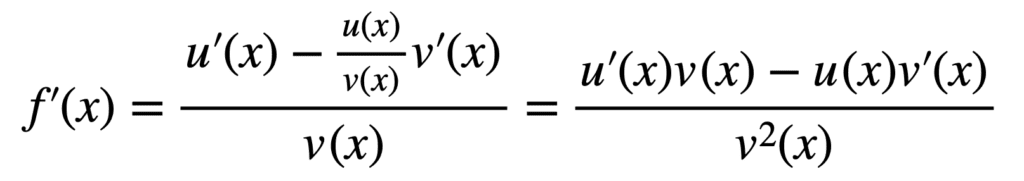
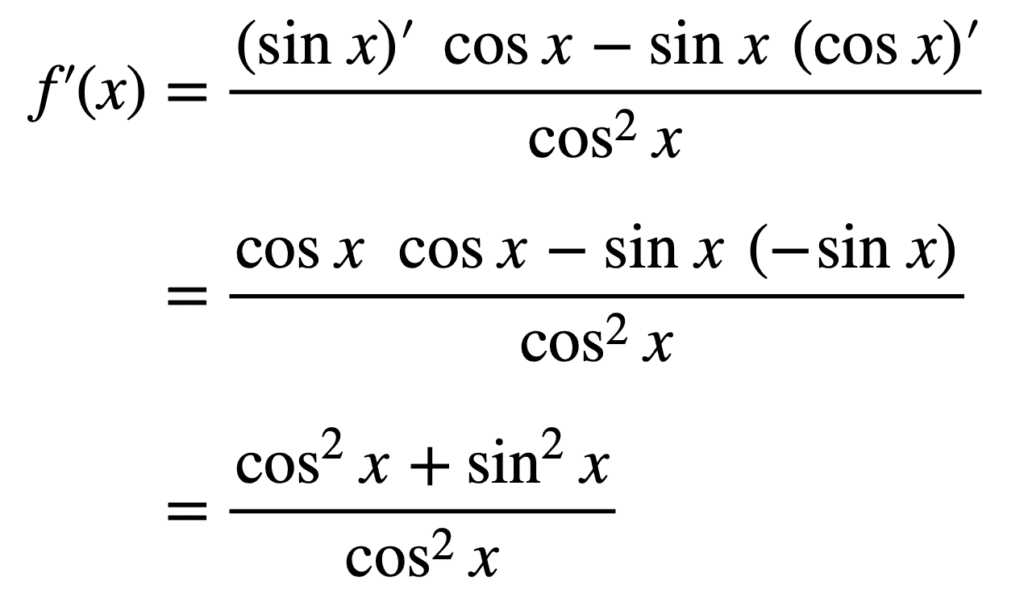
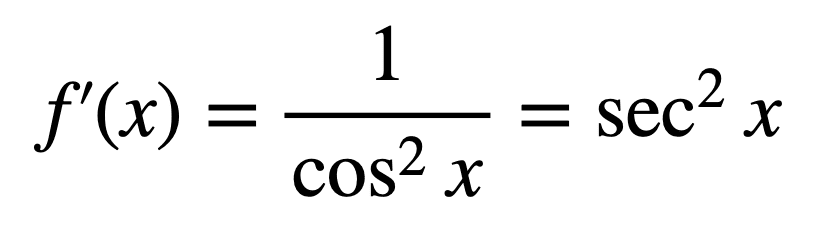





你不能说“我们开始吧”。那是杰森的口号。
哈哈哈。现在它可能是“机器学习精通”的口号了!
我事先得到了他的允许 🙂
我完全同意休·布朗的观点,因为我们应该在现实世界中使用机器学习。
尊敬的 Stefania 博士和 Jason 博士,
“我们开始吧” = “Ejja nibdew”
谢谢你
悉尼的Anthony
的确,安东尼,你的马耳他语是对的 🙂
尊敬的斯蒂芬妮娅博士,
我使用了谷歌翻译,英语 > 马耳他语。
然后为了确保翻译成马耳他语的内容尽可能接近英语,我从马耳他语 > 英语进行了翻译。
通常,如果一个人从英语 > 语言1 > 语言2 > .... > 语言X > 英语进行翻译,当极端化时,(i)在意义上会有上下文的丢失,以及(ii)语法错误,特别是在句子中的数量一致性方面。
谢谢你,
悉尼的Anthony