Transformer 注意力机制

在 Transformer 模型出现之前，用于神经机器翻译的注意力机制是通过基于 RNN 的编码器-解码器架构实现的。Transformer 模型通过摒弃循环和卷积，转而完全依赖自注意力机制，彻底改变了注意力的实现方式。

在本教程中，我们将首先关注 Transformer 注意力机制，然后在另一个教程中回顾 Transformer 模型。

在本教程中，您将了解用于神经机器翻译的 Transformer 注意力机制。

完成本教程后，您将了解：

• Transformer 注意力与其前身有何不同
• Transformer 如何计算缩放点积注意力
• Transformer 如何计算多头注意力

用我的书《使用注意力构建 Transformer 模型》来**启动您的项目**。它提供了**自学教程**和**可运行代码**，指导您构建一个功能完备的 Transformer 模型，该模型可以
将句子从一种语言翻译成另一种语言的完整 Transformer 模型...

让我们开始吧。

Transformer 注意力机制
图片来自Andreas Gücklhorn，部分权利保留。

教程概述

本教程分为两部分；它们是

• Transformer 注意力简介
• Transformer 注意力
  • 缩放点积注意力
  • 多头注意力

先决条件

本教程假设您已熟悉以下内容：

• 注意力的概念
• 注意力机制
• Bahdanau 注意力机制
• Luong 注意力机制

Transformer 注意力简介

至此，您已经熟悉了将注意力机制与基于 RNN 的编码器-解码器架构结合使用。以这种方式实现注意力的两种最流行的模型是 Bahdanau 等人 (2014) 和 Luong 等人 (2015) 提出的模型。

Transformer 架构通过摒弃循环和卷积（前述模型曾广泛依赖于此）彻底改变了注意力的使用方式。

……Transformer 是第一个完全依赖自注意力来计算其输入和输出表示，而不使用序列对齐的 RNN 或卷积的转导模型。

—— 《Attention Is All You Need》，2017。

在他们的论文《Attention Is All You Need》中，Vaswani 等人 (2017) 解释说，Transformer 模型转而完全依赖自注意力，其中通过关联同一序列中的不同词来计算序列（或句子）的表示。

自注意力，有时也称为内部注意力，是一种注意力机制，用于关联单个序列的不同位置，以计算该序列的表示。

—— 《Attention Is All You Need》，2017。

Transformer 注意力

Transformer 注意力使用的主要组成部分如下

• $\mathbf{q}$ 和 $\mathbf{k}$ 分别表示维度为 $d_k$ 的向量，包含查询和键
• $\mathbf{v}$ 表示维度为 $d_v$ 的向量，包含值
• $\mathbf{Q}$、$\mathbf{K}$ 和 $\mathbf{V}$ 分别表示打包了一组查询、键和值的矩阵。
• $\mathbf{W}^Q$、$\mathbf{W}^K$ 和 $\mathbf{W}^V$ 表示用于生成查询、键和值矩阵的不同子空间表示的投影矩阵
• $\mathbf{W}^O$ 表示多头输出的投影矩阵

本质上，注意力函数可以被视为查询与一组键值对到输出的映射。

输出计算为值的加权和，其中分配给每个值的权重由查询与对应键的兼容性函数计算。

—— 《Attention Is All You Need》，2017。

Vaswani 等人提出了*缩放点积注意力*，并在此基础上提出了*多头注意力*。在神经机器翻译的背景下，用作这些注意力机制输入的查询、键和值是同一输入句子的不同投影。

因此，直观地讲，所提出的注意力机制通过捕获同一句子不同元素（在此例中为单词）之间的关系来实现自注意力。

缩放点积注意力

Transformer 实现了一个缩放点积注意力，它遵循您之前见过的通用注意力机制的程序。

顾名思义，缩放点积注意力首先计算每个查询 $\mathbf{q}$ 与所有键 $\mathbf{k}$ 的*点积*。然后，它将每个结果除以 $\sqrt{d_k}$，并继续应用 softmax 函数。通过这样做，它获得了用于*缩放*值 $\mathbf{v}$ 的权重。

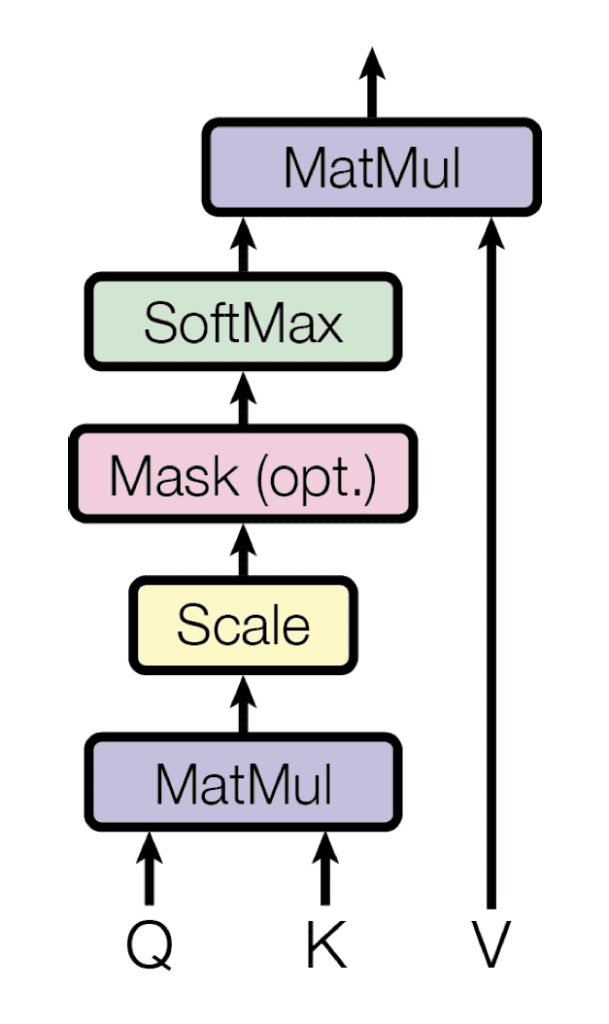
缩放点积注意力
摘自“Attention Is All You Need”

实际上，缩放点积注意力执行的计算可以同时高效地应用于整个查询集。为此，矩阵 $\mathbf{Q}$、$\mathbf{K}$ 和 $\mathbf{V}$ 作为输入提供给注意力函数

$$\text{attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right) V$$

Vaswani 等人解释说，他们的缩放点积注意力与 Luong 等人 (2015) 的乘法注意力相同，只是多了一个缩放因子 $\tfrac{1}{\sqrt{d_k}}$。

引入这个缩放因子是为了抵消 $d_k$ 值较大时点积幅度变大的影响，因为在这种情况下，应用 softmax 函数会返回极小的梯度，从而导致臭名昭著的梯度消失问题。因此，缩放因子有助于降低点积乘法生成的结果，从而防止此问题。

Vaswani 等人进一步解释说，他们选择乘法注意力而不是 Bahdanau 等人 (2014) 的加法注意力是基于前者相关的计算效率。

……点积注意力在实践中更快、空间效率更高，因为它可以使用高度优化的矩阵乘法代码实现。

—— 《Attention Is All You Need》，2017。

因此，计算缩放点积注意力的分步过程如下：

1. 通过将矩阵 $\mathbf{Q}$ 中打包的查询集与矩阵 $\mathbf{K}$ 中的键相乘来计算对齐分数。如果矩阵 $\mathbf{Q}$ 的大小为 $m \times d_k$，矩阵 $\mathbf{K}$ 的大小为 $n \times d_k$，则结果矩阵的大小将为 $m \times n$。

$$
\mathbf{QK}^T =
\begin{bmatrix}
e_{11} & e_{12} & \dots & e_{1n} \\
e_{21} & e_{22} & \dots & e_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
e_{m1} & e_{m2} & \dots & e_{mn} \\
\end{bmatrix}
$$

2. 将每个对齐分数按 $\tfrac{1}{\sqrt{d_k}}$ 缩放

$$
\frac{\mathbf{QK}^T}{\sqrt{d_k}} =
\begin{bmatrix}
\tfrac{e_{11}}{\sqrt{d_k}} & \tfrac{e_{12}}{\sqrt{d_k}} & \dots & \tfrac{e_{1n}}{\sqrt{d_k}} \\
\tfrac{e_{21}}{\sqrt{d_k}} & \tfrac{e_{22}}{\sqrt{d_k}} & \dots & \tfrac{e_{2n}}{\sqrt{d_k}} \\
\vdots & \vdots & \ddots & \vdots \\
\tfrac{e_{m1}}{\sqrt{d_k}} & \tfrac{e_{m2}}{\sqrt{d_k}} & \dots & \tfrac{e_{mn}}{\sqrt{d_k}} \\
\end{bmatrix}
$$

3. 然后，在缩放过程之后应用 softmax 操作以获得一组权重

$$
\text{softmax} \left( \frac{\mathbf{QK}^T}{\sqrt{d_k}} \right) =
\begin{bmatrix}
\text{softmax} ( \tfrac{e_{11}}{\sqrt{d_k}} & \tfrac{e_{12}}{\sqrt{d_k}} & \dots & \tfrac{e_{1n}}{\sqrt{d_k}} ) \\
\text{softmax} ( \tfrac{e_{21}}{\sqrt{d_k}} & \tfrac{e_{22}}{\sqrt{d_k}} & \dots & \tfrac{e_{2n}}{\sqrt{d_k}} ) \\
\vdots & \vdots & \ddots & \vdots \\
\text{softmax} ( \tfrac{e_{m1}}{\sqrt{d_k}} & \tfrac{e_{m2}}{\sqrt{d_k}} & \dots & \tfrac{e_{mn}}{\sqrt{d_k}} ) \\
\end{bmatrix}
$$

4. 最后，将所得权重应用于大小为 $n \times d_v$ 的矩阵 $\mathbf{V}$ 中的值

$$
\begin{aligned}
& \text{softmax} \left( \frac{\mathbf{QK}^T}{\sqrt{d_k}} \right) \cdot \mathbf{V} \\
=&
\begin{bmatrix}
\text{softmax} ( \tfrac{e_{11}}{\sqrt{d_k}} & \tfrac{e_{12}}{\sqrt{d_k}} & \dots & \tfrac{e_{1n}}{\sqrt{d_k}} ) \\
\text{softmax} ( \tfrac{e_{21}}{\sqrt{d_k}} & \tfrac{e_{22}}{\sqrt{d_k}} & \dots & \tfrac{e_{2n}}{\sqrt{d_k}} ) \\
\vdots & \vdots & \ddots & \vdots \\
\text{softmax} ( \tfrac{e_{m1}}{\sqrt{d_k}} & \tfrac{e_{m2}}{\sqrt{d_k}} & \dots & \tfrac{e_{mn}}{\sqrt{d_k}} ) \\
\end{bmatrix}
\cdot
\begin{bmatrix}
v_{11} & v_{12} & \dots & v_{1d_v} \\
v_{21} & v_{22} & \dots & v_{2d_v} \\
\vdots & \vdots & \ddots & \vdots \\
v_{n1} & v_{n2} & \dots & v_{nd_v} \\
\end{bmatrix}
\end{aligned}
$$

多头注意力

基于他们接收矩阵 $\mathbf{Q}$、$\mathbf{K}$ 和 $\mathbf{V}$ 作为输入的单一注意力函数（正如您刚刚回顾的），Vaswani 等人还提出了一种多头注意力机制。

他们的多头注意力机制将查询、键和值线性投影 $h$ 次，每次使用不同的学习投影。然后，单一注意力机制并行应用于这 $h$ 个投影中的每一个，以产生 $h$ 个输出，这些输出又被连接起来并再次投影以产生最终结果。

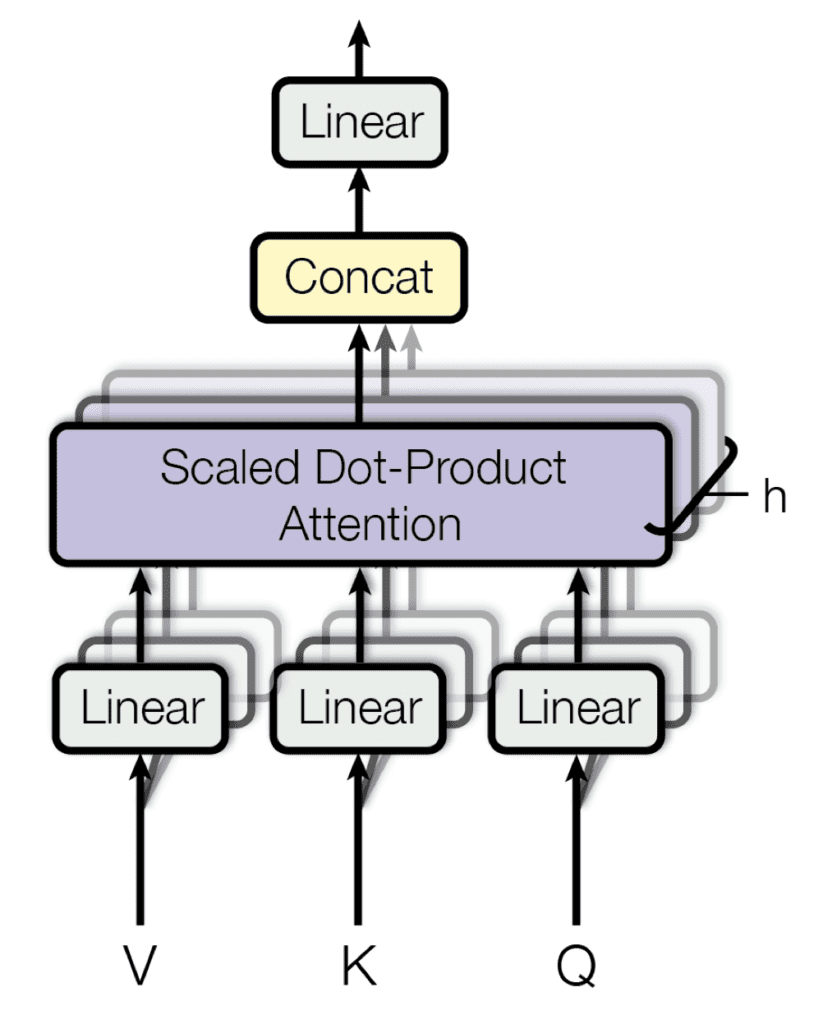
多头注意力
摘自“Attention Is All You Need”

多头注意力背后的思想是允许注意力函数从不同的表示子空间中提取信息，这在单一注意力头的情况下是不可能实现的。

多头注意力函数可以表示如下

$$\text{multihead}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{concat}(\text{head}_1, \dots, \text{head}_h) \mathbf{W}^O$$

这里，每个 $\text{head}_i$，$i = 1, \dots, h$，实现了一个由其自己的学习投影矩阵表征的单一注意力函数

$$\text{head}_i = \text{attention}(\mathbf{QW}^Q_i, \mathbf{KW}^K_i, \mathbf{VW}^V_i)$$

因此，计算多头注意力的分步过程如下：

1. 通过与各自的权重矩阵 $\mathbf{W}^Q_i$、$\mathbf{W}^K_i$ 和 $\mathbf{W}^V_i$ 相乘来计算查询、键和值的线性投影版本，每个 $\text{head}_i$ 对应一个。

2. 通过 (1) 将查询和键矩阵相乘，(2) 应用缩放和 softmax 操作，以及 (3) 对值矩阵加权，为每个头生成一个输出，从而为每个头应用单一注意力函数。

3. 连接各头的输出，即 $\text{head}_i$，$i = 1, \dots, h$。

4. 通过与权重矩阵 $\mathbf{W}^O$ 相乘，对连接后的输出进行线性投影，以生成最终结果。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

• 使用 Python 进行高级深度学习, 2019.

论文

• 注意力就是一切 (Attention Is All You Need), 2017。
• 通过联合学习对齐和翻译的神经机器翻译, 2014.
• 基于注意力的神经机器翻译的有效方法, 2015.

总结

在本教程中，您了解了用于神经机器翻译的 Transformer 注意力机制。

具体来说，你学到了：

• Transformer 注意力与其前身有何不同。
• Transformer 如何计算缩放点积注意力。
• Transformer 如何计算多头注意力。

你有什么问题吗？
在下面的评论中提出您的问题，我将尽力回答。

学习 Transformer 和注意力！

教您的深度学习模型阅读句子

...使用带有注意力的 Transformer 模型

在我的新电子书中探索如何实现
使用注意力机制构建 Transformer 模型

它提供了自学教程和可运行代码，指导您构建一个可以
将句子从一种语言翻译成另一种语言的完整 Transformer 模型...

为理解人类语言提供神奇力量
您的项目

查看内容