如何使用 Python 检查时间序列数据是否平稳

作者： Jason Brownlee 发布于 2020年8月15日分类：时间序列 183条评论

时间序列与传统分类和回归预测建模问题不同。

时间结构为观测值添加了顺序。这种强制的顺序意味着需要专门处理关于这些观测值一致性的重要假设。

例如，在建模时，假设观测值的汇总统计量是一致的。在时间序列术语中，我们将这种期望称为时间序列的平稳性。

这些假设很容易在时间序列中通过添加趋势、季节性和其他时间相关结构而被违反。

在本教程中，您将学习如何使用Python检查您的时间序列是否平稳。

完成本教程后，您将了解：

如何使用线图识别明显的平稳和非平稳时间序列。
如何检查均值和方差等汇总统计量随时间的变化。
如何使用具有统计显著性的统计检验来检查时间序列是否平稳。

通过我的新书《使用Python进行时间序列预测》启动您的项目，其中包括分步教程和所有示例的Python源代码文件。

让我们开始吧。

2017年2月更新：修正了p值解释中的打字错误，添加了要点使其更清晰。
2018年5月更新：改进了关于拒绝与未能拒绝统计检验的表述。
2019 年 4 月更新：更新了数据集链接。
2019年8月更新：更新了数据加载以使用新的API。
2019年11月更新：更新了Python 3的均值/方差示例，还更新了数据加载中的错误（感谢John）。

How to Check if Time Series Data is Stationary with Python

如何使用 Python 检查时间序列数据是否平稳
图片来源：Susanne Nilsson，保留部分权利。

平稳时间序列

平稳时间序列中的观测值不依赖于时间。

如果时间序列没有趋势或季节性效应，则它们是平稳的。在时间序列上计算的汇总统计量随时间保持一致，例如观测值的均值或方差。

当时间序列平稳时，建模会更容易。统计建模方法假设或要求时间序列平稳才能有效。

下载数据集并将其保存为：daily-total-female-births.csv.

下面是加载平稳的“每日女性出生人数”数据集的示例。

from pandas import read_csv
from matplotlib import pyplot
series = read_csv('daily-total-female-births.csv', header=0, index_col=0)
series.plot()
pyplot.show()

from pandas import read_csv

from matplotlib import pyplot

series = read_csv('daily-total-female-births.csv', header=0, index_col=0)

series.plot()

pyplot.show()

运行该示例会创建以下图表。

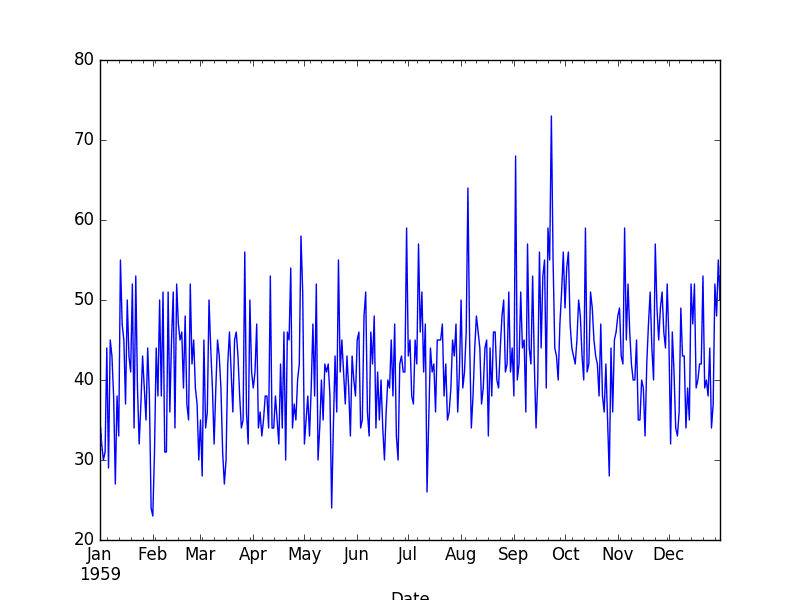
每日女性出生人数数据集图

停止以慢速学习时间序列预测！

参加我的免费7天电子邮件课程，了解如何入门（附带示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

非平稳时间序列

非平稳时间序列的观测值显示出季节性效应、趋势和其他依赖于时间索引的结构。

均值和方差等汇总统计量随时间变化，导致模型可能试图捕捉的概念发生漂移。

经典时间序列分析和预测方法关注于通过识别和消除趋势以及消除季节性效应来使非平稳时间序列数据平稳。

下载数据集并将其保存为：international-airline-passengers.csv.

下面是航空公司乘客数据集的示例，该数据集是非平稳的，显示了趋势和季节性成分。

from pandas import read_csv
from matplotlib import pyplot
series = read_csv('international-airline-passengers.csv', header=0, index_col=0)
series.plot()
pyplot.show()

from pandas import read_csv

from matplotlib import pyplot

series = read_csv('international-airline-passengers.csv', header=0, index_col=0)

series.plot()

pyplot.show()

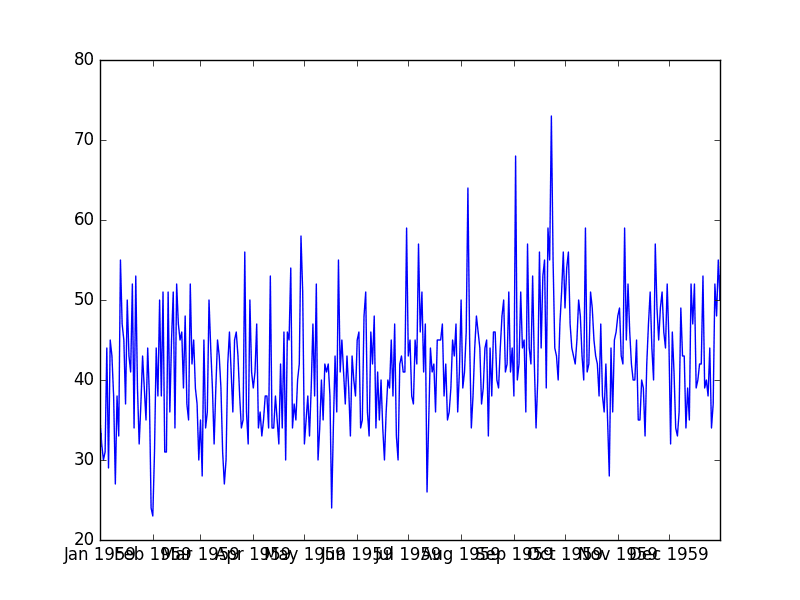
运行该示例会创建以下图表。

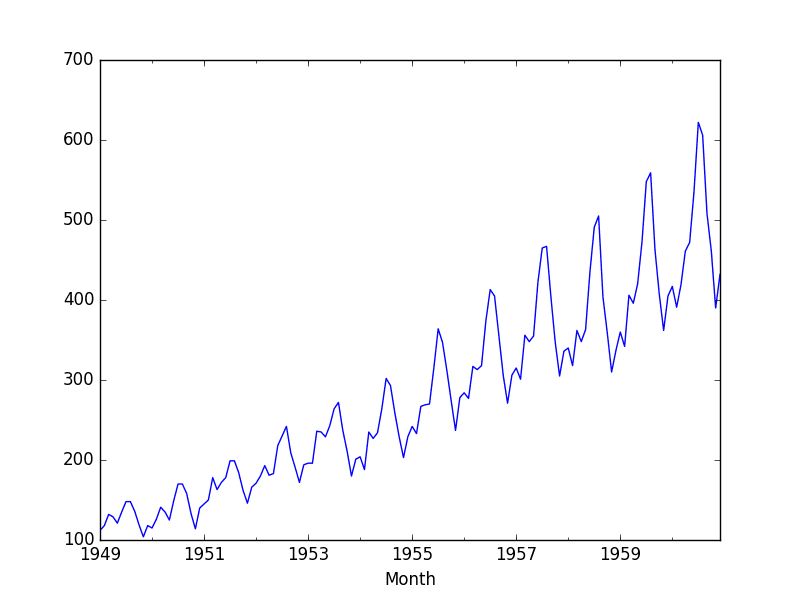
Non-Stationary Airline Passengers Dataset

非平稳航空公司乘客数据集

平稳时间序列的类型

平稳性概念源于时间序列的理论研究，在预测时是一种有用的抽象。

如果您深入研究此主题，可能会遇到一些更精细的平稳性概念。它们是：

它们是

平稳过程：生成平稳序列观测值的过程。
平稳模型：描述平稳序列观测值的模型。
趋势平稳：不表现出趋势的时间序列。
季节性平稳：不表现出季节性的时间序列。
严格平稳：平稳过程的数学定义，具体指观测值的联合分布对时间平移是不变的。

平稳时间序列和预测

您是否应该使您的时间序列平稳？

一般来说，是的。

如果您的时间序列中存在明显的趋势和季节性，那么对这些成分进行建模，从观测值中移除它们，然后对残差训练模型。

如果我们对数据拟合平稳模型，我们假设我们的数据是平稳过程的实现。因此，我们分析的第一步应该是检查是否存在趋势或季节性效应的证据，如果存在，则将其移除。

— 第122页，《R语言时间序列入门》。

统计时间序列方法甚至现代机器学习方法都将受益于数据中更清晰的信号。

但是…

当经典方法失效时，我们转向机器学习方法。当我们想要更多或更好的结果时。我们无法知道如何最好地建模时间序列数据中未知的非线性关系，有些方法在处理非平稳观测值或问题中的平稳和非平稳视图的某种混合时可能会产生更好的性能。

这里的建议是，在使用机器学习方法时，将时间序列是否平稳的属性视为另一个信息来源，可用于时间序列问题中的特征工程和特征选择。

平稳性检查

有许多方法可以检查时间序列（直接观测值、残差等）是平稳的还是非平稳的。

查看图表：您可以查看数据的时间序列图，并目视检查是否存在任何明显的趋势或季节性。
汇总统计量：您可以查看数据在季节或随机分区上的汇总统计量，并检查是否存在明显或显著的差异。
统计检验：您可以使用统计检验来检查是否满足或违反了平稳性期望。

上面，我们已经分别介绍了“每日女性出生人数”和“航空公司乘客”数据集，它们分别是平稳的和非平稳的，图表显示了趋势和季节性成分的明显缺失和存在。

接下来，我们将介绍一种快速粗略的方法，用于计算和审查时间序列数据集的汇总统计量，以检查其是否平稳。

描述性统计

检查时间序列是否非平稳的一种快速粗略方法是审查汇总统计量。

您可以将时间序列分成两个（或更多）分区，并比较每个组的均值和方差。如果它们不同且差异具有统计显著性，则时间序列很可能非平稳。

接下来，让我们在“每日出生人数”数据集上尝试这种方法。

每日出生人数数据集

由于我们关注的是均值和方差，我们假设数据符合高斯（也称为钟形曲线或正态）分布。

我们也可以通过目视检查观测值的直方图来快速验证这一点。

from pandas import read_csv
from matplotlib import pyplot
series = read_csv('daily-total-female-births.csv', header=0, index_col=0)
series.hist()
pyplot.show()

from pandas import read_csv

from matplotlib import pyplot

series = read_csv('daily-total-female-births.csv', header=0, index_col=0)

series.hist()

pyplot.show()

运行该示例会绘制时间序列值的直方图。我们清楚地看到了高斯分布的钟形曲线状，可能有一个较长的右尾。

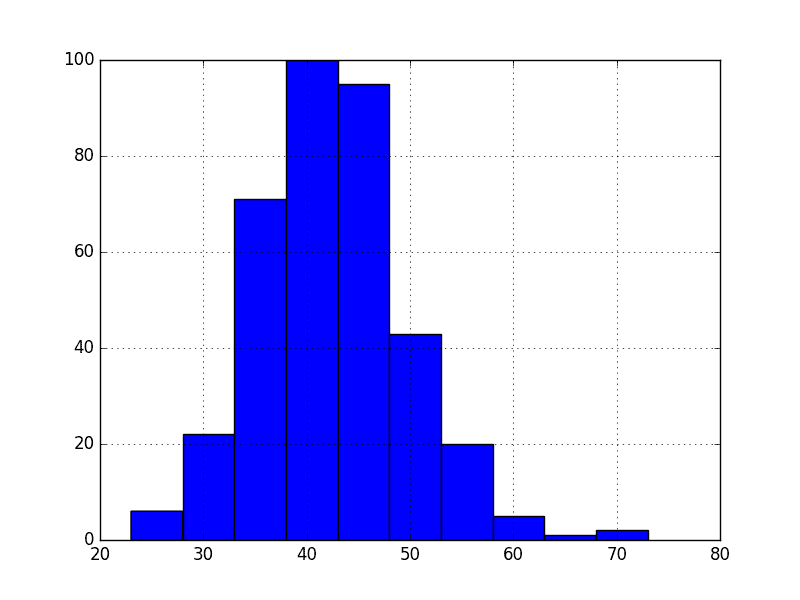
每日女性出生人数直方图

接下来，我们可以将时间序列分成两个连续序列。然后我们可以计算每组数字的均值和方差并比较这些值。

from pandas import read_csv
series = read_csv('daily-total-female-births.csv', header=0, index_col=0)
X = series.values
split = round(len(X) / 2)
X1, X2 = X[0:split], X[split:]
mean1, mean2 = X1.mean(), X2.mean()
var1, var2 = X1.var(), X2.var()
print('mean1=%f, mean2=%f' % (mean1, mean2))
print('variance1=%f, variance2=%f' % (var1, var2))

from pandas import read_csv

series = read_csv('daily-total-female-births.csv', header=0, index_col=0)

X = series.values

split = round(len(X) / 2)

X1, X2 = X[0:split], X[split:]

mean1, mean2 = X1.mean(), X2.mean()

var1, var2 = X1.var(), X2.var()

print('mean1=%f, mean2=%f' % (mean1, mean2))

print('variance1=%f, variance2=%f' % (var1, var2))

运行此示例显示均值和方差值不同，但在同一范围内。

mean1=39.763736, mean2=44.185792
variance1=49.213410, variance2=48.708651

1 2	mean1=39.763736, mean2=44.185792 variance1=49.213410, variance2=48.708651

接下来，让我们在“航空公司乘客”数据集上尝试相同的技巧。

航空公司乘客数据集

直截了当地说，我们可以分割数据集并计算每个组的均值和方差。

from pandas import read_csv
series = read_csv('international-airline-passengers.csv', header=0, index_col=0)
X = series.values
split = len(X) / 2
X1, X2 = X[0:split], X[split:]
mean1, mean2 = X1.mean(), X2.mean()
var1, var2 = X1.var(), X2.var()
print('mean1=%f, mean2=%f' % (mean1, mean2))
print('variance1=%f, variance2=%f' % (var1, var2))

from pandas import read_csv

series = read_csv('international-airline-passengers.csv', header=0, index_col=0)

X = series.values

split = len(X) / 2

X1, X2 = X[0:split], X[split:]

mean1, mean2 = X1.mean(), X2.mean()

var1, var2 = X1.var(), X2.var()

print('mean1=%f, mean2=%f' % (mean1, mean2))

print('variance1=%f, variance2=%f' % (var1, var2))

运行该示例，我们可以看到均值和方差看起来非常不同。

我们有一个非平稳时间序列。

mean1=182.902778, mean2=377.694444
variance1=2244.087770, variance2=7367.962191

1 2	mean1=182.902778, mean2=377.694444 variance1=2244.087770, variance2=7367.962191

好吧，也许。

让我们退一步，通过将时间序列值绘制为直方图来检查在这种情况下假设高斯分布是否有意义。

from pandas import read_csv
from matplotlib import pyplot
series = read_csv('international-airline-passengers.csv', header=0, index_col=0)
series.hist()
pyplot.show()

from pandas import read_csv

from matplotlib import pyplot

series = read_csv('international-airline-passengers.csv', header=0, index_col=0)

series.hist()

pyplot.show()

运行该示例显示，值的分布确实不像高斯分布，因此均值和方差值的意义较小。

这种被压扁的观测值分布可能是非平稳时间序列的另一个指标。

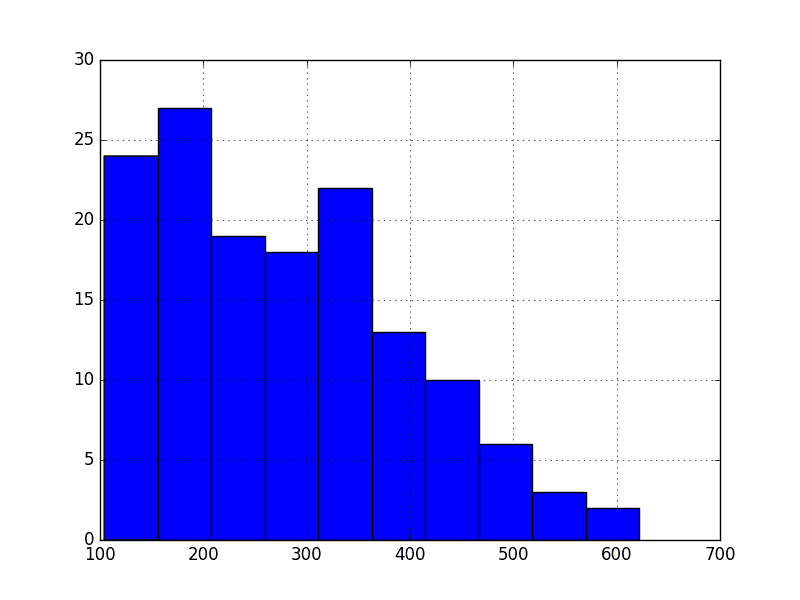
航空公司乘客直方图

再次查看时间序列图，我们可以看到存在明显的季节性成分，并且季节性成分似乎正在增长。

这可能表明季节到季节的指数增长。可以使用对数变换将指数变化展平回线性关系。

下面是经过对数变换的时间序列的相同直方图。

from pandas import read_csv
from matplotlib import pyplot
from numpy import log
series = read_csv('international-airline-passengers.csv', header=0, index_col=0)
X = series.values
X = log(X)
pyplot.hist(X)
pyplot.show()
pyplot.plot(X)
pyplot.show()

from pandas import read_csv

from matplotlib import pyplot

from numpy import log

series = read_csv('international-airline-passengers.csv', header=0, index_col=0)

X = series.values

X = log(X)

pyplot.hist(X)

pyplot.show()

pyplot.plot(X)

pyplot.show()

运行该示例，我们可以看到更熟悉的高斯状或均匀状值分布。

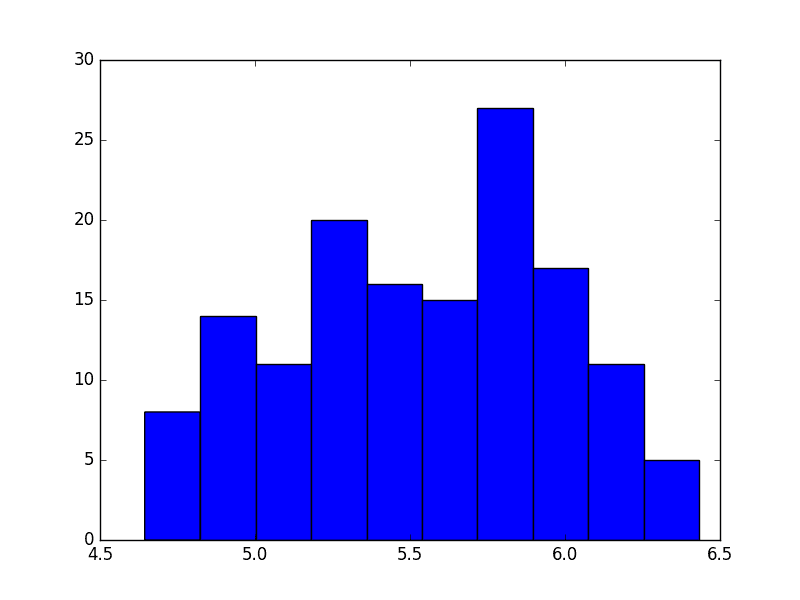
航空公司乘客对数直方图

我们还创建了对数变换数据的线图，可以看到指数增长似乎有所减弱，但我们仍然有趋势和季节性元素。

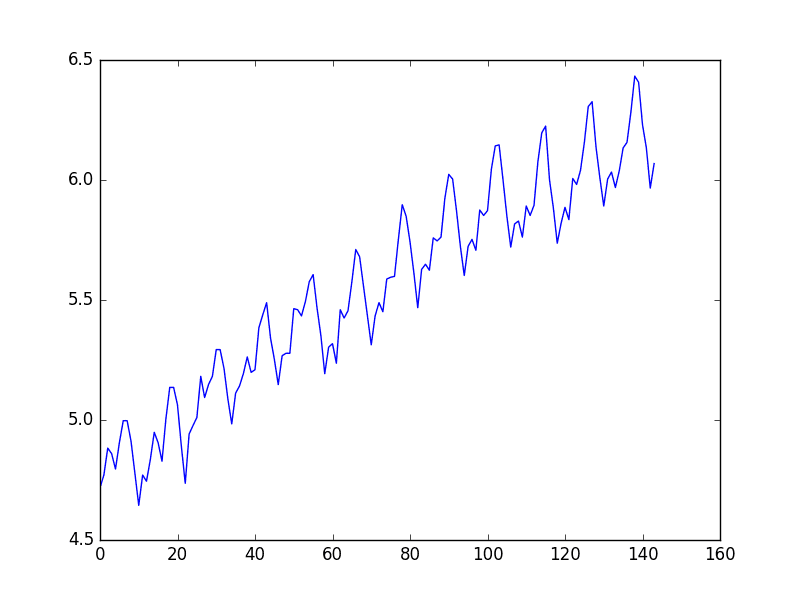
航空公司乘客对数线图

现在我们可以计算对数变换数据集的均值和标准差。

from pandas import read_csv
from matplotlib import pyplot
from numpy import log
series = read_csv('international-airline-passengers.csv', header=0, index_col=0)
X = series.values
X = log(X)
split = round(len(X) / 2)
X1, X2 = X[0:split], X[split:]
mean1, mean2 = X1.mean(), X2.mean()
var1, var2 = X1.var(), X2.var()
print('mean1=%f, mean2=%f' % (mean1, mean2))
print('variance1=%f, variance2=%f' % (var1, var2))

from pandas import read_csv

from matplotlib import pyplot

from numpy import log

series = read_csv('international-airline-passengers.csv', header=0, index_col=0)

X = series.values

X = log(X)

split = round(len(X) / 2)

X1, X2 = X[0:split], X[split:]

mean1, mean2 = X1.mean(), X2.mean()

var1, var2 = X1.var(), X2.var()

print('mean1=%f, mean2=%f' % (mean1, mean2))

print('variance1=%f, variance2=%f' % (var1, var2))

运行示例显示每组的均值和标准差值再次相似，但不完全相同。

也许，仅从这些数字来看，我们会说时间序列是平稳的，但从线图来看，我们强烈认为情况并非如此。

mean1=5.175146, mean2=5.909206
variance1=0.068375, variance2=0.049264

1 2	mean1=5.175146, mean2=5.909206 variance1=0.068375, variance2=0.049264

这是一种可能很容易被误导的快速粗略方法。

我们可以使用统计检验来检查两个高斯随机变量样本之间的差异是真实的还是统计巧合。我们可以探索统计显著性检验，如学生t检验，但由于值之间的序列相关性，事情变得复杂。

在下一节中，我们将使用专门用于判断单变量时间序列是否平稳的统计检验。

增广迪基-富勒检验

统计检验对您的数据做出强假设。它们只能用于说明拒绝或未能拒绝零假设的程度。结果必须针对给定问题进行解释才能有意义。

尽管如此，它们可以提供快速检查和确认证据，表明您的时间序列是平稳的还是非平稳的。

增广迪基-富勒检验是一种称为单位根检验的统计检验。

单位根检验的直观原理是它确定时间序列受趋势影响的强度。

存在多种单位根检验，增广迪基-富勒检验可能是使用更广泛的检验之一。它使用自回归模型，并在多个不同滞后值上优化信息准则。

该检验的零假设是时间序列可以用单位根表示，即它不是平稳的（具有某种时间相关结构）。备择假设（拒绝零假设）是时间序列是平稳的。

零假设 (H0)：如果未能拒绝，则表明时间序列具有单位根，意味着它非平稳。它具有某种时间相关结构。
备择假设 (H1)：拒绝零假设；它表明时间序列不具有单位根，意味着它平稳。它不具有时间相关结构。

我们使用检验的p值来解释这个结果。p值低于阈值（例如5%或1%）表明我们拒绝零假设（平稳），否则p值高于阈值表明我们未能拒绝零假设（非平稳）。

p值 > 0.05：未能拒绝零假设 (H0)，数据具有单位根且非平稳。
p值 <= 0.05：拒绝零假设 (H0)，数据不具有单位根且平稳。

下面是在“每日女性出生人数”数据集上计算增广迪基-富勒检验的示例。statsmodels库提供了实现该检验的adfuller()函数。

from pandas import read_csv
from statsmodels.tsa.stattools import adfuller
series = read_csv('daily-total-female-births.csv', header=0, index_col=0, squeeze=True)
X = series.values
result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
	print('\t%s: %.3f' % (key, value))

from pandas import read_csv

from statsmodels.tsa.stattools import adfuller

series = read_csv('daily-total-female-births.csv', header=0, index_col=0, squeeze=True)

X = series.values

result = adfuller(X)

print('ADF Statistic: %f' % result[0])

print('p-value: %f' % result[1])

print('Critical Values:')

for key, value in result[4].items():

print('\t%s: %.3f' % (key, value))

运行此示例会打印检验统计量值为-4。该统计量越负，我们越有可能拒绝零假设（我们有一个平稳数据集）。

作为输出的一部分，我们得到一个查找表来帮助确定ADF统计量。我们可以看到我们的统计量值-4小于1%时的值-3.449。

这表明我们可以以低于1%的显著性水平拒绝零假设（即结果是统计巧合的概率很低）。

拒绝零假设意味着该过程没有单位根，进而意味着时间序列是平稳的或不具有时间相关结构。

ADF Statistic: -4.808291
p-value: 0.000052
Critical Values:
	5%: -2.870
	1%: -3.449
	10%: -2.571

ADF统计量：-4.808291

p值：0.000052

临界值

5%: -2.870

1%: -3.449

10%: -2.571

我们可以在航空公司乘客数据集上执行相同的测试。

from pandas import read_csv
from statsmodels.tsa.stattools import adfuller
series = read_csv('international-airline-passengers.csv', header=0, index_col=0, squeeze=True)
X = series.values
result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
	print('\t%s: %.3f' % (key, value))

from pandas import read_csv

from statsmodels.tsa.stattools import adfuller

series = read_csv('international-airline-passengers.csv', header=0, index_col=0, squeeze=True)

X = series.values

result = adfuller(X)

print('ADF Statistic: %f' % result[0])

print('p-value: %f' % result[1])

print('Critical Values:')

for key, value in result[4].items():

print('\t%s: %.3f' % (key, value))

运行该示例给出了与上述不同的情况。检验统计量是正的，这意味着我们不太可能拒绝零假设（它看起来是非平稳的）。

将检验统计量与临界值进行比较，看起来我们不得不未能拒绝时间序列非平稳且确实具有时间相关结构的零假设。

ADF Statistic: 0.815369
p-value: 0.991880
Critical Values:
	5%: -2.884
	1%: -3.482
	10%: -2.579

ADF统计量：0.815369

p值：0.991880

临界值

5%: -2.884

1%: -3.482

10%: -2.579

让我们再次对数据集进行对数变换，以使值的分布更趋线性，并更好地满足此统计检验的期望。

from pandas import read_csv
from statsmodels.tsa.stattools import adfuller
from numpy import log
series = read_csv('international-airline-passengers.csv', header=0, index_col=0, squeeze=True)
X = series.values
X = log(X)
result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
for key, value in result[4].items():
	print('\t%s: %.3f' % (key, value))

from pandas import read_csv

from statsmodels.tsa.stattools import adfuller

from numpy import log

series = read_csv('international-airline-passengers.csv', header=0, index_col=0, squeeze=True)

X = series.values

X = log(X)

result = adfuller(X)

print('ADF Statistic: %f' % result[0])

print('p-value: %f' % result[1])

for key, value in result[4].items():

print('\t%s: %.3f' % (key, value))

运行该示例显示检验统计量为负值。

我们可以看到该值大于临界值，再次意味着我们无法拒绝零假设，进而意味着时间序列是非平稳的。

ADF Statistic: -1.717017
p-value: 0.422367
	5%: -2.884
	1%: -3.482
	10%: -2.579

ADF统计量：-1.717017

p值：0.422367

5%: -2.884

1%: -3.482

10%: -2.579

总结

在本教程中，您学习了如何使用Python检查时间序列是否平稳。

具体来说，你学到了：

时间序列数据对于统计建模方法甚至一些现代机器学习方法而言，其平稳性至关重要。
如何使用线图和基本汇总统计量来检查时间序列是否平稳。
如何计算和解释统计显著性检验以检查时间序列是否平稳。

您对平稳和非平稳时间序列，或对这篇帖子有任何疑问吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

Python中用于数据准备和时间序列预测的移动平均平滑

Python中用于时间序列预测的自回归模型

对《如何使用Python检查时间序列数据是否平稳》的183条回复

Eduardo Gonzatti 2016年12月30日上午6:08 #

你好，很棒的帖子！

只是一个简单的问题，当测试两个价格序列之间OLS回归的残差平稳性时，如果ADF检验拒绝了残差上的H0，您会认为这两个价格序列是协整的吗？
或者您会首先对每个价格序列运行ADF检验，以查看它们本身是否是I(1)？

谢谢！

回复
- Jason Brownlee 2016年12月31日上午7:00 #
  
  你好，Eduardo，
  
  两者都检查。我会检查输入数据和残差。
  
  回复
  - adedayo abraham 2017年6月1日晚上8:12 #
    
    您能提供有关此项目主题的材料吗？比较时间序列数据平稳化的不同方法。您可以通过此邮箱联系我：adedayo.temmy@yahoo.com。谢谢。
    
    回复
Eduardo Gonzatti 2017年1月6日晚上10:46 #

嗨，Jason，
谢谢回复！

我问这个问题是因为一个“常识性”（也许不是）的假设，即价格序列本身并非平稳，所以有时我会问自己这种测试是否有点多余。

此致！

回复
- Jason Brownlee 2017年1月7日上午8:39 #
  
  我非常看好机器学习方法在时间序列上的应用，而不是ARIMA等线性方法，但一个非常重要的考虑因素是平稳性。
  
  趋势去除和季节性探索至关重要，否则机器学习方法会因与线性方法相同的原因而崩溃。
  
  我想写一系列关于平稳性的文章。
  
  回复
  - Naira Grigoryan 2018年10月16日上午4:16 #
    
    您好。有哪些方法适合检查时间序列是否
    
    1. 有趋势
    2. 平稳
    3. 有季节性
    
    我想通过RNN进行时间序列预测，但为了获得更准确的结果，我需要在开始时检查所有这3个特征。
    
    回复
    - Jason Brownlee 2018年10月16日上午6:39 #
      
      数据可视化是一个好的开始。
      
      回复
Cipher 2017年1月8日晚上11:50 #

除了使用log，您是否考虑使用panda.diff()？

回复
- Jason Brownlee 2017年1月9日上午7:51 #
  
  谢谢 Cipher，它比手动做差分要好。
  
  回复
  - Asieh 2019年8月28日上午4:09 #
    
    嗨，Jason，
    
    我不太确定为什么在航空公司数据集的情况下，您也检查了对数。因为第一次测试显示数据不是平稳的。您为什么还要对对数进行测试呢？换句话说，假设对数上的adfuller测试显示该数据集的对数是平稳的；这仍然没有改变数据集本身是非平稳的事实。
    
    回复
    - Jason Brownlee 2019年8月28日上午6:42 #
      
      像对数这样的幂变换可以消除非平稳方差——正如我们在这个数据集中看到的那样。
      
      回复
      - edgar panganiban 2019年10月14日下午3:47 #
        
        我想他的意思是当你对非平稳方差进行幂变换（对数）并对其进行测试（adf）并构建模型时。这只适用于变换后的数据。但是原始的、未变换的数据集呢？
      - Jason Brownlee 2019年10月15日上午6:04 #
        
        我们不再使用原始数据，而是使用变换后的数据。我们继续应用变换，直到得到平稳数据，然后拟合模型。
        
        这有帮助吗？
Seine Yumnam 2017年1月19日上午2:26 #

很棒的文章！易于理解。简单就是力量。还有所有这些好东西。

回复
- Jason Brownlee 2017年1月19日上午7:34 #
  
  谢谢 Seine。我很高兴你觉得它有用。
  
  回复
jack kinkade 2017年2月28日上午5:55 #

“我们使用检验的p值来解释这个结果。p值低于阈值（例如5%或1%）表明我们接受零假设（非平稳），否则表明我们拒绝零假设（平稳）”

这不应该与您所说的相反吗？请参阅http://stats.stackexchange.com/questions/55805/how-do-you-interpret-results-from-unit-root-tests

回复
- Jason Brownlee 2017年2月28日上午8:30 #
  
  你好，Jack，
  
  是的，那是一个错别字，现在正在修复，我还用一些要点使其更清晰。帖子中的所有分析都是正确的。
  
  总之，零假设（H0）是存在单位根（自回归是非平稳的）。拒绝它意味着没有单位根且非平稳。
  
  p值大于临界值意味着我们不能拒绝H0，我们接受存在单位根且数据是非平稳的。
  
  回复
  - Amine Ait el harraj 2018年4月9日晚上10:29 #
    
    你好Jason，感谢您撰写如此精彩的文章，但我认为您纠正错误的方式是相反的，如果我没记错的话，它更像是“我们使用测试的p值来解释这个结果。p值低于阈值（例如5%或1%）表明我们接受零假设（平稳），否则表明我们拒绝零假设（非平稳）”
    
    回复
    - Amine Ait el harraj 2018年4月9日晚上10:32 #
      
      我的错，是正确的，我把它和平稳性检验的H0搞混了
      
      回复
      - Jason Brownlee 2018年4月10日上午6:20 #
        
        没问题。这确实令人困惑。
    - Miro 2019年6月26日上午12:49 #
      
      自回归不一定是非平稳的。例如，AR(1)。
      
      回复
Magnus 2017年3月31日上午1:57 #

我用我自己的数据集进行了增广迪基-富勒检验。我的结果如下：
ADF统计量：-34.360229
p值：0.000000
临界值
1%: -3.430
5%: -2.862
10%: -2.567
所以我的时间序列是平稳的。在我的例子中，我有525600个值，最大滞后为102。这些是一个月的分钟数据。但我不明如何如此少的滞后就能检测出例如每日变化？
现在当我计算发生频率的分布时，在每小时分箱的数据上，UT上明显存在时间依赖性。在某个值范围内，大约在15 UT时，我比其他时间有更多的样本。所以我的数据中存在UT依赖性，但它仍然是平稳的。所以我猜在使用这个测试时应该小心。在我的例子中，存在UT依赖性的是值数量，而不是值本身。如何处理这个问题？一个想法可能是将时间的正弦和余弦添加到输入中。对此有什么评论吗？

回复
- Jason Brownlee 2017年3月31日上午5:56 #
  
  有意思。也许值得在不同的时间尺度上进行平稳性测试？
  
  回复
  - Magnus 2017年4月1日上午1:50 #
    
    是的，我做了。结果相同。我还对您之前帖子中的太阳黑子数进行了测试。我得到了这个结果
    ADF统计量：-9.567668
    p值：0.000000
    临界值
    1%: -3.433
    5%: -2.863
    10%: -2.567
    现在，我真的很困惑。我还对一个正弦函数的人工数据进行了测试，该函数添加了正态分布数据。现在测试给出的p值为0.07，但从图表上看，数据明显是非平稳的。所以我真的建议使用Pandas中的分组处理并绘制数据。
    另一种方法，不是去除季节性，而是以下方法。如果只有用于训练预测模型的目标值是非平稳的，那么将时间的正弦/余弦添加到输入中可能会更容易。当然，输入空间会增加，但对于这些输入，不需要创建滞后数据。
    我感谢任何评论和建议。
    
    回复
    - Jason Brownlee 2017年4月19日上午7:58 #
      
      我对你的结果表示怀疑。
      
      我发现这个测试是可靠的。
      
      也许statsmodels库的版本过时了，或者您加载的数据与您的预期不符？
      
      回复
    - abdulwahid gul 2018年10月29日上午2:17 #
      
      问题在于您打印结果的方式。您可以像这样打印整个变量
      print(result)
      
      或类似这样
      print(‘ADF Statistic: {}’.format(result[0])).
      
      我以前也有同样的问题，但更改打印格式后，就解决了。
      ADF统计量：-12.851066
      p值：0.000000
      临界值
      1%: -3.431
      5%: -2.862
      10%: -2.567
      
      回复
Joy 2017年4月1日上午4:02 #

迪基-富勒检验结果
检验统计量 -1.152597e+01
p值 3.935525e-21
使用的滞后数 2.300000e+01
使用的观测数 1.417000e+03
临界值 (5%) -2.863582e+00
临界值 (1%) -3.434973e+00
临界值 (10%) -2.567857e+00
dtype: float64

你好，我想预测我的时间序列数据集的温度。Python中的迪基-富勒检验给出了以上结果，显示检验统计量大于任何临界值，这意味着经过变换后时间序列不是平稳的。那么，我可以在时间序列非平稳的情况下进行预测吗？

回复
- Jason Brownlee 2017年4月1日上午5:59 #
  
  可以，但可以考虑再进行一轮差分。
  
  回复
- Clarke 2018年1月30日晚上7:33 #
  
  Joy，您用了什么代码来得到这个结果？我正试图得到这样的结果，但我只得到了图表
  
  回复
Ritesh Kumar 2017年7月24日晚上8:13 #

statsmodel python 库是否要求我们将序列转换为平稳序列，然后才能将序列输入任何 ARMA 或 ARIMA 模型？

回复
- Jason Brownlee 2017年7月25日上午9:41 #
  
  理想情况下，我会这样做。模型可以进行差分以处理趋势，但我建议事先明确地预处理数据。这将帮助您更好地理解您的问题/数据。
  
  回复
Francois3C 2017年11月5日下午4:25 #

很棒的文章，您让这些话题变得易懂。

我开始测试一些序列的平稳性，并得到了一些我无法理解的奇怪行为。

在 Python (3.6) 中，ADF 对 100 和 101 个项目的线性序列给出了如此不同的结果

from statsmodels.tsa.stattools import adfuller
adfuller(range(100))
adfuller(range(101))

给出的ADF统计量分别为+2.59和-4.23。

我期望这两个结果非常接近。两者都不是平稳序列，因为它们表达相同的趋势。但测试在一个案例中是正的，在另一个案例中是负的。

有什么问题吗？

回复
- Jason Brownlee 2017年11月6日上午4:50 #
  
  我不会担心，重点关注测试（例如，值相对于临界值），而不是值本身。
  
  回复
  - Francois3C 2017年11月6日下午5:10 #
    
    感谢您的快速回复。
    
    但这正是我的问题：对于一个斜率/趋势恒为+1的序列，观察值的微小变化会导致测试结果从非平稳完全转向平稳，其原因我无法理解。
    
    from statsmodels.tsa.stattools import adfuller
    X=range(100)
    result = adfuller(X)
    print(‘ADF统计量：%f’ % result[0])
    print(‘p值：%f’ % result[1])
    for key, value in result[4].items()
    print(‘\t%s: %.3f’ % (key, value))
    
    ADF统计量：2.589283
    p值：0.999073
    1%: -3.505
    5%: -2.894
    10%: -2.584
    
    X=range(101)
    result = adfuller(X)
    print(‘ADF统计量：%f’ % result[0])
    print(‘p值：%f’ % result[1])
    for key, value in result[4].items()
    print(‘\t%s: %.3f’ % (key, value))
    
    ADF统计量：-4.232578
    p值：0.000580
    1%: -3.504
    5%: -2.894
    10%: -2.584
    
    回复
    - Jason Brownlee 2017年11月7日上午9:46 #
      
      啊，我明白了。这可能是统计检验需要临界最小值数据才能可行的情况。
      
      回复
Choubix 2017年11月30日晚上10:15 #

感谢分享知识！
如果您不介意，我有几个快速问题：我想在ETF上测试一些交易策略。这些时间序列显然是非平稳的。
如何将它们转换为平稳的？
我想使用技术指标（其输入是价格）作为模型中的特征。我应该如何处理这些特征？
我的目标不是预测价格，而是分类为“买入/卖出”（或持有）。
有什么算法更适合金融时间序列吗？

谢谢！

回复
- Jason Brownlee 2017年12月1日上午7:34 #
  
  您可以使用差分和季节性调整。我写过关于这两种方法的文章，请使用搜索功能。
  
  回复
foyle 2017年12月7日上午8:24 #

实际上，当ADF统计量 < 临界值时，它是平稳的。将p值与临界值进行比较是不正确的，而且令人困惑。包括adfuller API解释在https://statsmodels.cn/dev/generated/statsmodels.tsa.stattools.adfuller.html。

回复
- Jason Brownlee 2017年12月7日下午3:03 #
  
  我不认为我们在这篇文章中比较 p 值和任何东西，我相信我们正在审查检验统计量。
  
  回复
  - foyle 2017年12月7日晚上11:31 #
    
    我明白了。当ADF统计量 < 临界值或p值 < 阈值时，序列是平稳的。阈值是0.05等。
    
    回复
    - Jason Brownlee 2017年12月8日上午5:41 #
      
      也许我比较迟钝，但具体在哪里？你能引用一下原文吗？
      
      我注意到我分别描述了如何解释p值和如何解释检验统计量。
      
      回复
    - foyle 2017年12月8日上午8:28 #
      
      来自您的博客。
      p值 <= 0.05：拒绝零假设 (H0)，数据不具有单位根且平稳。
      
      还有另一种基于临界值的解释。
      
      https://www.analyticsvidhya.com/blog/2016/02/time-series-forecasting-codes-python/
      
      因此，有两种方法可以考虑adfuller的结果，使用p值或使用临界值。
      
      回复
      - Jason Brownlee 2017年12月8日下午2:29 #
        
        在那一节中，我只是在介绍p值的含义，而不是如何解释测试。抱歉造成困惑。
Dima Burlaj 2017年12月22日晚上9:05 #

我进行了迪基-富勒检验，p值为1。然后我进行了Box_Cox变换，这使得p值下降到0.96。然后我进行了季节性差分，p值下降到0.0000。之后，我构建了LSTM神经网络并对其进行训练。现在，我想比较原始尺度和变换后的结果。我找到了scipy.special.inv_boxcox()函数，它执行逆变换。但对我来说，它不起作用。可能是哪里出错了？

回复
- Jason Brownlee 2017年12月23日上午5:17 #
  
  也许您可以在模型之外的一些测试数据上进行实验。先变换，再逆变换。
  
  请记住，所有操作都需要逆转，包括季节性调整。
  
  回复
Prashanth 2018年2月2日晚上10:00 #

太棒了！

回复
- Jason Brownlee 2018年2月3日上午8:37 #
  
  谢谢。
  
  回复
TAMER A. FARRAG 2018年4月23日上午3:14 #

Jason，我对您的文章非常感兴趣，我有一个问题。

如果我使用残差数据（去除季节性和趋势）训练我的模型，那么预测值如何获得正确的值（如何再次添加季节性和趋势）。

我希望我能正确地提出我的问题。抱歉我的英语不好。

补充说明，

您为什么不使用“statsmodels”包来分解时间序列。我的意思是这里讨论的问题

https://stackoverflow.com/questions/20672236/time-series-decomposition-function-in-python

回复
- Jason Brownlee 2018年4月23日上午6:21 #
  
  如果您在建模之前去除了趋势和季节性，您可以将它们加回到预测中。
  
  如果您使用了差分，则反转差分。如果您使用了模型，则反转模型的应用。
  
  我的博客上有很多这样的例子。
  
  回复
  - Joe Herro 2019年3月24日上午9:15 #
    
    嗨 Jason，
    
    我正在寻找上面提到的关于如何在去除趋势和季节性后重新将其添加到模型中的博客文章。您能告诉我涵盖此内容的博客文章吗？我似乎找不到它们。
    
    非常感谢，
    
    Joe
    
    回复
    - Jason Brownlee 2019年3月25日上午6:39 #
      
      如果您通过差分去除趋势或通过季节性差分去除季节性，您可以直接通过与被减去的值相加来将其添加回来。
      
      也许这会有帮助。
      https://machinelearning.org.cn/machine-learning-data-transforms-for-time-series-forecasting/
      
      回复
Fauzan Taufik 2018年5月23日上午2:58 #

你好Jason，据我所知，adfuller是随机游走的统计检验，H1意味着非随机游走，上面你揭示H1也意味着平稳时间序列，难道任何非随机游走都是平稳的吗？

回复
- Jason Brownlee 2018年5月23日上午6:30 #
  
  该测试检查是否存在单位根
  https://en.wikipedia.org/wiki/Augmented_Dickey%E2%80%93Fuller_test
  
  随机游走不是平稳的。
  
  回复
  - Arthur 2018年6月14日下午1:27 #
    
    我认为值得一提的是，要应用ADF检验，我们假设时间序列遵循给定模型（dy(t)=cst+gamma*y(t-1)+….+e(t)），其中e(t)是误差项，应该是一个白噪声。
    
    所以如果你拒绝H0，并且误差项确实是白噪声且gamma<1，那么模型将是平稳的（我认为是严格意义上的——参见https://people.maths.bris.ac.uk/~magpn/Research/LSTS/TOS.html了解平稳性的不同定义）
    
    回复
    - Jason Brownlee 2018年6月14日下午4:07 #
      
      谢谢您的留言。
      
      回复
Denis 2018年6月1日上午2:38 #

回溯（最近一次调用）
文件“shampoo.py”，第20行，在
result = adfuller(X)
文件“/home/denis/.local/lib/python3.5/site-packages/statsmodels/tsa/stattools.py”，第221行，在adfuller中
xdall = lagmat(xdiff[:, None], maxlag, trim='both', original='in')
文件“/home/denis/.local/lib/python3.5/site-packages/statsmodels/tsa/tsatools.py”，第397行，在lagmat中
nobs, nvar = xa.shape
ValueError: 要解包的值太多 (预期为2)

回复
- Jason Brownlee 2018年6月1日上午8:24 #
  
  我在这里有一些建议
  https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
  
  回复
nabila 2018年8月31日晚上11:46 #

嗨，Jason，

很棒的教程！我刚开始接触时间序列数据，所以我想知道，如果我的数据未能通过平稳性测试，那么我就不能对其进行时间序列分析，对吗？RNN可以对非平稳时间序列进行建模吗？

回复
- Jason Brownlee 2018年9月1日上午6:21 #
  
  你可以，但结果可能不好。
  
  根据我的经验，RNN在平稳序列上的表现确实更好。
  
  回复
Aishwarya Singh 2018年9月12日晚上7:42 #

你好，

我猜趋势平稳序列是那些有趋势但没有单位根的序列。如果我错了请纠正我。

参考：http://in.mathworks.com/help/econ/trend-stationary-vs-difference-stationary.html

回复
Krishna 2018年9月17日晚上10:31 #

嗨，Jason，
我有一个小问题，当您使用ADF时，如果结果表明是平稳的，它是差分平稳、增量平稳还是时间序列中的普通弱平稳......

回复
- Jason Brownlee 2018年9月18日上午6:15 #
  
  统计检验报告的是平稳的可能性，而不是事实。
  
  回复
Dmitry 2018年9月25日上午4:38 #

我正在处理一个时间序列，其中每个时间点都有多个随机测量值。换句话说，我的X系列包含每个时间戳的一组不同的测量值。

所描述的程序和代码是否可以直接用于我的情况？我应该对这些X进行排序吗？

回复
- Jason Brownlee 2018年9月25日上午6:30 #
  
  您需要分别处理每个时间序列（变量）。
  
  回复
amelie BM 2018年9月25日晚上11:50 #

谢谢您的解释！这很有趣
模型评估后，我们如何可视化预测数据以完善现有数据库

谢谢

回复
- Jason Brownlee 2018年9月26日上午6:16 #
  
  谢谢。您可以使用matplotlib的plot()函数绘制yhat与y。
  
  回复
ML Uros 2018年10月12日上午5:28 #

你好 Jason。在上面的例子中，您使用 ADF 来测试高斯正态分布样本是否平稳。1) 如果我们尝试建模一个显示非高斯分布的过程，有什么提示吗？2) 我们仍然可以根据非高斯过程的两个子样本的均值/方差对平稳性进行推断吗？3) 您能给我提供一些关于如何测试非正态样本的平稳性以及如何建模此类时间序列的参考文献吗？谢谢！

回复
- Jason Brownlee 2018年10月12日上午6:45 #
  
  好问题，使用数据可视化始终是一个很好的备用方案。
  
  回复
Lahiru 2018年10月17日晚上8:13 #

我需要Bai Perron检验、KPSS检验和Phillips Perron检验的代码

回复
- Jason Brownlee 2018年10月18日上午6:26 #
  
  也许可以谷歌搜索一下？
  
  回复
Volka 2018年11月20日下午1:03 #

你好，这是一个非常有趣的教程。非常感谢。

我有大约1000多个不同格式为（年份，数字）的时间序列数据集，需要预测每个数据集未来5年的值。由于数据集很多，我想知道是否有一种方法可以自动化上述平稳性检查步骤，以便我可以直接执行ARIMA过程？或者您有什么其他算法推荐？

回复
- Jason Brownlee 2018年11月20日下午2:06 #
  
  也许在建模之前对所有数据集进行差分？
  
  回复
  - Volka 2018年11月21日下午4:23 #
    
    非常感谢您的建议。您的意思是将“log”作为“差分”执行吗？之后再使用增广迪基-富勒检验的p值来判断平稳性吗？
    
    只是好奇，执行“log”是否能保证您有一个平稳的时间序列数据集？
    
    回复
    - Jason Brownlee 2018年11月22日上午6:21 #
      
      对数和其他幂变换可以平息递增/变化的方差，并使数据分布更接近高斯分布。
      
      回复
mk 2018年12月11日下午2:31 #

对数变换不起作用，这种情况下我们该怎么做？
谢谢。

回复
- Jason Brownlee 2018年12月11日下午2:34 #
  
  你说的“不工作”是什么意思？
  
  回复
  - mk 2018年12月11日下午5:44 #
    
    事实是时间序列仍然是非平稳的。我们如何获得平稳时间序列？
    
    回复
    - Jason Brownlee 2018年12月12日上午5:50 #
      
      你可以通过差分法去除趋势，通过季节性差分法去除季节性。
      
      我写过关于这两个主题的文章，也许可以从这里开始
      https://machinelearning.org.cn/start-here/#timeseries
      
      回复
Lukasz 2019年1月10日下午8:48 #

谢谢杰森，很棒的文章。
但是，您能否就多元、多输入和多输出时间序列的平稳性测试方法提供建议？
我正在为数千个不同元素进行多步预测。对于每个元素，我可能需要使用几种不同类型的测量值（例如温度、压力、交通等）。我必须为每个站点预测三个时间序列。对于某些网络元素，测量值上升，而对于其他元素，测量值下降……在这种情况下，我应该如何正确进行平稳性测试？我应该单独检查和转换每个元素吗？还是对每个按时间聚合的测量值（在整个元素集上）执行平稳性测试？您有什么建议？
此致。

回复
- Jason Brownlee 2019年1月11日上午7:44 #
  
  我会先对每个单独的单变量序列进行测试。
  
  然后测试使一个或所有序列平稳是否会影响模型性能，例如线性模型。
  
  回复
  - Lukasz 2019年1月23日下午8:28 #
    
    谢谢 Jason！
    
    回复
Hector Alvaro Rojas 2019年2月3日下午11:22 #

我有一个关于您对“国际航空乘客”数据集应用的增广迪基-富勒（ADF）测试的问题。当使用R应用ADF测试时，我们得到的结果与使用Python时不同。以下是数据。

使用R

library(tseries)
tsData <- AirPassengers # ts data
adf.test(as.timeseries(tsData)) # p-value < 0.05 indicates the TS is stationary

输出

增广迪基-富勒检验

数据：tsData
迪基-富勒 = -7.3186，滞后阶数 = 5，p值 = 0.01
备择假设：平稳

警告信息
In adf.test(tsData) : p-value smaller than printed p-value

结论：拒绝原假设。所以我们接受它是平稳的。

使用Python

from pandas import Series
from statsmodels.tsa.stattools import adfuller
series = Series.from_csv('daily-total-female-births.csv', header=0)
X = series.values
result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items()
print('\t%s: %.3f' % (key, value))

输出
ADF统计量：0.815369
p值：0.991880
临界值
5%: -2.884
1%: -3.482
10%: -2.579

结论：不拒绝原假设。所以我们不接受它是平稳的。那么它看起来是非平稳的。
检验统计量为正，这意味着我们拒绝原假设的可能性要小得多（它看起来是非平稳的）。

两个数据集（R：AirPassengers 和 Python：daily-total-female-births）是相同的。所以，我无法找出ADF测试显示不同结果的原因。

您能否帮助我解释这种罕见的情况？

回复
- Jason Brownlee 2019年2月4日上午5:48 #
  
  航空数据集不是平稳的。如果某个库报告它是平稳的，那么您的代码或该库中可能存在错误？
  
  回复
  - Hector Alvaro Rojas 2019年2月7日下午11:41 #
    
    正确的R代码是
    
    library(tseries)
    tsData <- AirPassengers # ts data
    adf.test(tsData)
    
    AirPassengers
    
    输出
    一月二月三月四月五月六月七月八月九月十月十一月十二月
    1949 112 118 132 129 121 135 148 148 136 119 104 118
    1950 115 126 141 135 125 149 170 170 158 133 114 140
    1951 145 150 178 163 172 178 199 199 184 162 146 166
    1952 171 180 193 181 183 218 230 242 209 191 172 194
    1953 196 196 236 235 229 243 264 272 237 211 180 201
    1954 204 188 235 227 234 264 302 293 259 229 203 229
    1955 242 233 267 269 270 315 364 347 312 274 237 278
    1956 284 277 317 313 318 374 413 405 355 306 271 306
    1957 315 301 356 348 355 422 465 467 404 347 305 336
    1958 340 318 362 348 363 435 491 505 404 359 310 337
    1959 360 342 406 396 420 472 548 559 463 407 362 405
    1960 417 391 419 461 472 535 622 606 508 461 390 432
    
    class(AirPassengers)
    
    输出
    [1] "ts"
    
    frequency(AirPassengers)
    
    输出
    [1] 12
    
    我再次运行了测试，但现在使用您的数据集作为来源（将其转换为R中的“ts”类），我得到了相同的结果。
    
    无论如何，以这种方式使用R中的增广迪基-富勒（ADF）测试来呈现该数据集的平稳性研究，确实存在问题。
    
    网上有许多文章（www）仅使用ADF测试和R就得出AirPassengers数据集是平稳的结论，而这显然是不平稳的。
    
    我百分之百同意您的观点。我的意思是，如果我们在R中通过使用其他测试和自相关分析来补充我们的研究，我们可以得出AirPassengers数据集不是平稳数据集的相同结论。
    
    感谢您的回答和时间，当然。
    
    此致。
    
    HA
    
    回复
    - Jason Brownlee 2019年2月8日上午7:50 #
      
      有意思。也许是例程中存在错误，或者R中对测试的解释方式发生了变化？我认为后者可能性更大。
      
      回复
Alex Bietrix 2019年4月29日下午11:58 #

你好，
我有一个关于时间序列建模的问题。我在 Python 中实现了一个多重线性回归，但在 Eviews 上发现阈值回归会更好。

你知道如何用 Python 实现这个新模型吗？我暂时还没找到解决方案。

非常感谢您的回答。

Alex

回复
- Jason Brownlee 2019年4月30日上午6:59 #
  
  我对这个算法不熟悉，也许可以问问作者？
  
  回复
Min 2019年5月29日上午12:40 #

嗨，Jason，

很棒的帖子！我是时间序列分析的新手。我有问题想问您，高自相关图（即使滞后=100）是否意味着时间序列是非平稳的？因为我用了您所有的方法，数据似乎应该是平稳的，但绘制自相关图后，结果仍然很高。

回复
- Jason Brownlee 2019年5月29日上午8:45 #
  
  不一定，如果你在去除趋势和季节性后计算 ACF/PACF，它可能是平稳的并且仍然具有高相关性（我想——凭记忆）。
  
  回复
zik 2019年6月2日下午5:34 #

非常感谢教授。
我一直在尝试联系您，先生……
我的 ADF 检验结果是 -2，没有通过任何显著性检验，
你认为菲利普-佩伦检验是个好主意吗？

回复
- Jason Brownlee 2019年6月3日上午6:38 #
  
  抱歉，我不熟悉那个测试。
  
  回复
Shubham Kumar 2019年6月6日上午8:58 #

嗨，Jason，

很棒的内容！
如果在我的时间序列上应用ADF检验后，我得到了原假设为真，那么这意味着时间序列遵循随机游走过程。

这意味着试图使序列平稳将不起作用，对吗？因为随机游走意味着没有可学习的模式。

对序列进行差分将给我一个趋势平稳的时间序列，但方差非平稳。

我正确吗？或者有什么转换可以奏效吗？

回复
- Jason Brownlee 2019年6月6日下午2:16 #
  
  随机游走是非平稳的，但并非所有非平稳时间序列都是随机游走。
  
  尝试差分以使其平稳。
  
  回复
  - Shubham Kumar 2019年6月7日上午12:06 #
    
    但ADF不是在测试单位根的存在吗？单位根的存在意味着随机游走。这就是我困惑的地方：如果ADF零假设被接受，那么预测就不应该奏效。
    
    回复
    - Jason Brownlee 2019年6月7日上午8:03 #
      
      那不是我的理解。
      
      单位根意味着非平稳，可能是趋势非平稳。
      https://en.wikipedia.org/wiki/Dickey%E2%80%93Fuller_test
      
      回复
      - Shubham Kumar 2019年6月7日下午11:21 #
        
        好吧。我的错！
        
        所以随机游走特指Y(t-1)项系数为1且过程为AR(1)的情况？
        
        Xt = b0 + b1×X(t-1) + εt
        
        即随机游走是AR(1)过程的特例，其中 b1 = 1。
        
        这次对了，对吧？
      - Jason Brownlee 2019年6月8日上午6:56 #
        
        当然，更多内容请看这里
        https://machinelearning.org.cn/gentle-introduction-random-walk-times-series-forecasting-python/
Kimiya 2019年6月7日下午5:20 #

嗨！
感谢您的精彩内容！
我有一个问题，如果您能帮助我，我将不胜感激！
是否有可能我们在图中看到明显的趋势，但仍从迪基-富勒检验中得出时间序列是平稳的结果？

回复
- Jason Brownlee 2019年6月8日上午6:48 #
  
  可能不会。
  
  回复
vamsee krishna jagarlamudi 2019年6月13日上午12:38 #

我有一个小问题，如何引用您在此处展示的材料

回复
- vamsee krishna jagarlamudi 2019年6月13日上午12:40 #
  
  抱歉，主要是ADF测试案例的参考
  
  回复
- Jason Brownlee 2019年6月13日上午6:18 #
  
  我在这里展示如何做
  https://machinelearning.org.cn/faq/single-faq/how-do-i-reference-or-cite-a-book-or-blog-post
  
  回复
Anindya Sankar Chattopadhyay 2019年6月23日下午10:30 #

嗨 Jason

您有关于使用 Python 的 statsmodels 模块的 VAR 和 VARMAX 的文章吗？

对于这些模型，如何衡量预测误差（以 MAE 表示）？

谢谢

回复
- Jason Brownlee 2019年6月24日上午6:32 #
  
  我没有关于 VAR 或 VARMAX 的教程。
  
  是的，您可以使用 sklearn 来计算 MAE
  https://scikit-learn.cn/stable/modules/classes.html#sklearn-metrics-metrics
  
  回复
Amandeep 2019年6月23日下午11:27 #

嗨，Jason，

您有关于检查多元时间序列预测方法平稳性的文章吗？

如果您能分享使用 Python 的 VAR 模块，那将非常棒。

谢谢，
阿曼

回复
- Jason Brownlee 2019年6月24日上午6:32 #
  
  我没有，只有单变量数据。
  
  感谢您的建议。
  
  回复
André Araujo 2019年7月1日下午11:50 #

嗨，杰森，你还好吗？
如果我的时间序列中存在一些零，我该如何处理对数图？我的目标是预测降雨量。它不是平稳的。我遇到了一个错误，遵循这个方法：对零取对数。
谢谢。

回复
- Jason Brownlee 2019年7月2日上午7:33 #
  
  您可以通过向所有样本添加一个值来创建对数图，以确保所有值都为正。
  
  回复
Leen 2019年7月21日上午3:08 #

你好 Jason，

ADF统计量：-4.808291
p值：0.000052
临界值
5%: -2.870
1%: -3.449
10%: -2.571

这里，ADF 统计量为 -4，小于所有临界值，意味着我们拒绝原假设，但是 p 值 0.000052 大于 5% (-2.870)，所以我们无法拒绝原假设？我们应该怎么判断？

回复
- Leen 2019年7月21日上午3:09 #
  
  我的意思是，我们得到了相互矛盾的结果？
  
  回复
  - Jason Brownlee 2019年7月21日上午6:33 #
    
    不行。
    
    回复
- Jason Brownlee 2019年7月21日上午6:33 #
  
  p 值 <= 0.05 意味着我们拒绝。-4.808291 <= -3.449 意味着我们拒绝。两种情况都拒绝。
  
  回复
Leen 2019年7月21日上午3:25 #

抱歉，Jason，我忘了 p 值必须小于 0.05，而不是临界值 5%。我问完才发现错误 XD

回复
- Jason Brownlee 2019年7月21日上午6:34 #
  
  没关系，这可能会让人困惑。
  
  回复
Tejasvi 2019年8月4日下午4:49 #

嗨，Jason，

请澄清一下这句话——“单位根检验的直觉是它决定了时间序列受{趋势}定义有多强。”

我遇到一个“趋势平稳”但明显具有季节性的时间序列示例。ADF 报告的 p 值非常低。

所以，我很好奇，

1. 如果平稳性意味着没有趋势和季节性，是否有不同的测试来检查完全平稳性（趋势和季节性）？
2. 或者只要时间序列是趋势平稳的，模型就能很好地工作吗？

请指教。非常感谢。

回复
- Jason Brownlee 2019年8月5日上午6:47 #
  
  是的，如果存在季节性，它就不会是平稳的。通常，只谈论趋势会更简单，但你说得对。
  
  一个平稳的时间序列既没有趋势也没有季节性。
  
  回复
Loulou 2019年8月23日上午12:05 #

嗨，Jason，

如 statsmodel 文档所示

statsmodels.tsa.stattools.adfuller(x, maxlag=None, regression='c', autolag='AIC', store=False, regresults=False)

如果我们使用默认值，maxlag 默认为 12*(nobs/100)^{1/4}，并且选择滞后数以最小化相应的信息准则（在本例中为 AIC）

我的问题是
如果返回的滞后 result[2] 是 14，您知道我们必须取所有滞后到 14 还是只取第 14 个滞后吗？

提前感谢

回复
- Jason Brownlee 2019年8月23日上午6:31 #
  
  默认情况下，所有滞后直到第14个。
  
  为了在该区间内更具选择性地选择滞后，可能需要自定义模型。
  
  回复
Anna 2019年9月6日下午6:43 #

嗨，Jason，

我正在研究 VXO 和一些其他股票市场数据。
对于 VXO，季节性分解显示了一些趋势和强烈的季节性，但 AD-Test 表明数据是平稳的。我这里没有进行任何转换。
另一方面，对于 S&P500，我必须使用对数收益才能实现平稳性。这可能吗？我很难理解其中的区别。
如果这完全没问题：我可以使用这两个系列作为相同模型的输入（假设从 OLS 开始）吗，或者它们必须经过相同的处理，即相同的转换才能产生有用的结果？

非常感谢您的回复。

回复
- Jason Brownlee 2019年9月7日上午5:23 #
  
  不同的时间序列可能需要以不同的方式进行平稳化。一旦平稳，就可以对其进行建模。
  
  回复
Berns Buenaobra 2019年9月7日上午6:27 #

杰森博士再次出击！这篇文章给了我极大的启发！我的用例快完成了，但一位好同事却向我提出了我（大小，时间）配对数据最重要的测试——如果平稳，如何测试是否存在季节性？增广迪基-富勒测试是。再次感谢。

回复
- Jason Brownlee 2019年9月8日上午5:08 #
  
  很高兴它有帮助！
  
  如果存在季节性，则数据不是平稳的。
  
  回复
Sai 2019年9月27日下午3:54 #

你好，

我从迪基-富勒检验中得到以下结果。有人能建议使我的数据平稳的技术吗？

我可以看到实际数据、滚动均值、滚动标准差的图表模式也几乎相同。

我已经尝试了对数变换和差分，结果仍然相同 🙁

迪基-富勒检验结果
检验统计量 -8.161630e+00
p值 9.110753e-13
使用的滞后数 2.000000e+01
使用的观测值数量 1.351000e+03
临界值 (1%) -3.435200e+00
临界值 (5%) -2.863682e+00
临界值 (10%) -2.567910e+00
dtype: float64

此致，
Sai

回复
- Jason Brownlee 2019年9月28日上午6:10 #
  
  如果趋势和季节性都存在，也许可以尝试分别对趋势和季节性进行差分？
  
  https://machinelearning.org.cn/remove-trends-seasonality-difference-transform-python/
  
  还可以尝试Box-Cox幂变换吗？
  
  回复
edgar panganiban 2019年10月14日下午3:58 #

很棒的教程！我只有一个问题。我有一个方差很大的日期序列，作为解决方案，我对其进行了对数变换。问题是它改变了我的日期序列数据，当我进行预测时，它只根据那个改变/变换后的数据进行预测（尽管它极大地改进了我的模型，MSE 只有 1+ 而之前是 500+）。我如何才能将其恢复到可以实际预测真实值（但使用来自变换后日期序列的模型）的状态，或者在这种情况下需要什么方法……

回复
- Jason Brownlee 2019年10月15日上午6:06 #
  
  我不明白，抱歉。
  
  您在历史数据上拟合模型，然后使用该模型对未来进行预测。有时我们在拟合模型之前准备历史数据。
  
  您具体在哪里遇到困难？
  
  如果您需要帮助进行预测，例如调用 predict()，这可能会有所帮助
  https://machinelearning.org.cn/make-sample-forecasts-arima-python/
  
  回复
Karolina 2019年10月15日上午3:54 #

嗨，Jason，
感谢这篇帖子，非常有帮助。我对我数据进行了迪基-富勒检验，得到了一个零 p 值。
这意味着什么？我读到这可能意味着数据不具有正态分布且不平稳。可能吗？以下是检验结果
检验统计量 = -4.539
P 值 = 0.000
临界值
1%: -3.453342167806272
5%: -2.871663828287282
10%: -2.572164381381345

回复
- Jason Brownlee 2019年10月15日上午6:20 #
  
  这可能表明数据是平稳的。
  
  或许可以绘制图表来确认。
  
  回复
edgar panganiban 2019年10月21日下午2:01 #

很棒的教程，只有一个问题。如果最终发现时间序列数据是非平稳的。你会继续基于它构建模型吗？还是会寻找另一个可以更好地构建的时间序列数据？

回复
- Jason Brownlee 2019年10月22日上午5:40 #
  
  谢谢。
  
  你可以使用差分、季节性差分和幂变换使其平稳。
  
  回复
Felipe 2019年10月30日上午1:33 #

你好，Jason。

我有一个关于如何准备这个数据集（链接如下）的疑问。您能给个建议吗？

这似乎是一个非平稳序列，对吗？

原始数据集图
https://pasteboard.co/IEdYWWx.png

我尝试应用 365 天的差分法

diff = difference(values, 365)

差分后数据集图
https://pasteboard.co/IEe4rko.png

过程就是这样吗？

谢谢。

回复
- Jason Brownlee 2019年10月30日上午6:05 #
  
  是的，看起来有季节性。
  
  也许你需要进行两次季节性差分？
  
  回复
  - Felipe 2019年11月1日上午2:05 #
    
    你好，Jason。
    
    我必须用归一化数据还是非归一化数据评估 RMSE？
    
    RMSE 的结果对两者都一样吗？
    
    谢谢。
    
    回复
    - Jason Brownlee 2019年11月1日上午5:40 #
      
      通常，您在所有变换都反转后的数据上评估误差，以便单位与原始数据相同。
      
      回复
Karl 2019年10月30日上午10:18 #

好文章，杰森，谢谢！

我很好奇（假设我们之前不知道）哪个 X 或 Y 是自变量，反之亦然……有没有办法确定其中一个？

回复
- Jason Brownlee 2019年10月30日下午1:58 #
  
  也许你指的是相关性？例如
  https://machinelearning.org.cn/how-to-use-correlation-to-understand-the-relationship-between-variables/
  
  回复
Fahad 2019年11月17日上午3:10 #

嗨，Jason，

感谢您的邮件和所有一切。我仍然向您和您的书学习。
请问我关于如何使用 Python 检查时间序列数据是否平稳有两个问题。
我的原始数据有趋势，从均值和方差值的测试以及视觉观察来看，它有趋势。

你知道，要消除趋势，我需要应用一阶差分或二阶差分。

请问，应用差分法消除趋势会影响我的原始数据值吗？
请问，除了差分法之外，还有其他方法可以消除趋势吗？

谢谢你。

此致，

回复
- Jason Brownlee 2019年11月17日上午7:15 #
  
  是的，差分会改变你的原始数据，这就是目的。
  
  是的，你可以拟合一个线性模型并从数据中减去它。
  
  回复
John 2019年11月24日上午7:28 #

你好，我尝试运行您在这篇文章中展示的相同代码，似乎传入

from statsmodels.tsa.stattools import adfuller
series = read_csv('daily-total-female-births.csv', header=0, index_col=0)
X = series.values
result = adfuller(X)

显示以下错误

ValueError: 要解包的值太多 (预期为2)

我通过使用以下代码解决了这个问题

import statsmodels.tsa.stattools as tsa
series = read_csv('daily-total-female-births.csv', header=0, index_col=0)
result = tsa.adfuller(series['Births'])

我对上面显示的两个代码块之间的区别非常困惑。

很棒的网站，请继续努力。

约翰

回复
- John 2019年11月24日上午7:59 #
  
  我在代码中发现了一个小错误
  
  split = (len(X) / 2) ### 这对于女性出生率 csv 返回 182.5
  X1, X2 = X[0:split], X[split:]
  
  切片过程期望 X1 和 X2 为整数，因此如果 len(X) 为奇数，它会返回错误，
  
  我通过使用以下代码修复了这个问题
  split = round(len(X)/2)
  
  回复
  - Jason Brownlee 2019年11月24日上午9:25 #
    
    太棒了，谢谢！
    
    我已更新示例。
    
    回复
- Jason Brownlee 2019年11月24日上午9:24 #
  
  看起来是数据集加载中的一个错误。我一定是在更新中引入的。
  
  谢谢！已修复。
  
  回复
vania todorova 2019年12月21日上午8:03 #

你好 Jason，感谢所有教程！我对我时间序列数据进行了 ADF 检验，结果如下。你认为这意味着它是平稳的，我可以直接使用时间序列算法吗？谢谢！
迪基-富勒检验结果
检验统计量 -6.817677e+00
p值 2.039396e-09
使用的滞后数 6.000000e+00
使用的观测值数量 7.770000e+02
临界值 (1%) -3.438794e+00
临界值 (5%) -2.865267e+00
临界值 (10%) -2.568755e+00
dtype: float64

回复
- Jason Brownlee 2019年12月21日上午8:17 #
  
  它看起来是平稳的。
  
  回复
  - vania todorova 2019年12月24日上午3:54 #
    
    谢谢！如果我尝试对数据取对数，它会一直提示对数遇到除零错误。除了不使用数据的对数之外，有什么建议可以解决这个问题吗？谢谢！
    
    回复
    - Jason Brownlee 2019年12月24日上午6:44 #
      
      在进行对数变换之前，将数据变为正数。
      
      回复
Rajesh Swarnkar 2020年1月24日下午6:03 #

嗨，Jason，

我运行了 adfuller，输出如下

ADF 统计量：-2.457146
p 值：0.126252
临界值：1%：-3.438，5%：-2.865，10%：-2.569

https://github.com/RSwarnkar/temporary/blob/master/timeseries2.png

序列是平稳的还是非平稳的？

此致，
Rajesh

回复
- Jason Brownlee 2020年1月25日上午8:32 #
  
  非平稳。
  
  回复
Rajesh Swarnkar 2020年1月24日下午6:05 #

您是否计划在网站上增加登录功能，以便我查看我过去的评论和回复？

谢谢！

回复
- Rajesh Swarnkar 2020年1月24日下午6:08 #
  
  一个单独的讨论区也会很棒！
  
  回复
  - Jason Brownlee 2020年1月25日上午8:32 #
    
    好建议。
    
    回复
- Jason Brownlee 2020年1月25日上午8:32 #
  
  目前还没有。
  
  回复
ENRIQUE BONILLA 2020年2月1日上午7:10 #

你好，Jason

对于 Python 3.7 版本，第 4 行应添加一个缺失的类型转换。

from pandas import read_csv
series = read_csv('international-airline-passengers.csv', header=0, index_col=0)
X = series.values
split = int(len(X) / 2)
X1 = X[0:split]
X2 = X[split:]
mean1, mean2 = X1.mean(), X2.mean()
var1, var2 = X1.var(), X2.var()
print('mean1=%f, mean2=%f' % (mean1, mean2))
print('variance1=%f, variance2=%f' % (var1, var2))

其余代码示例均正常

E. Bonilla

回复
- Jason Brownlee 2020年2月2日上午6:17 #
  
  好建议，谢谢！
  
  回复
Devarshi Goswami 2020年2月12日下午5:56 #

以下是我的 adfuller() 函数的输出。
我理解这意味着我的时间序列是平稳的？是否还有其他可以从中推断出的解释？
我可以将此拟合到 ARIMA 模型中以预测未来值吗？

ADF 统计量：-4.453993
p 值：0.000238
临界值
1%: -3.433
5%: -2.863
10%: -2.567

回复
- Jason Brownlee 2020年2月13日上午5:38 #
  
  是的，平稳的。
  
  回复
Steve 2020年4月6日下午2:47 #

我目前正在使用这个库。您以前使用过吗？

https://alkaline-ml.com/pmdarima/modules/classes.html#arima-estimator-statistical-tests

回复
- Jason Brownlee 2020年4月7日上午5:36 #
  
  我没有，抱歉。
  
  回复
Marcus 2020年4月12日下午2:11 #

嗨，杰森。我刚做了 ADF 检验，得到了 p 值=0，检验统计量=-14，其他所有临界值都大于 -4。按照规则，我本可以接受该序列是平稳的。但问题是，在我查看其 acf 图后，该序列呈现出强烈的自相关。在图中，系数非常缓慢地下降到零，直到滞后变为 200，这与 ADF 检验的结果相矛盾。所以，我很好奇这是否真的会发生？或者只是我犯了错误。

回复
- Jason Brownlee 2020年4月13日上午6:10 #
  
  也许测试的假设被违反了，导致结果无效——只是猜测。
  
  也许可以把结果作为指导，专注于从模型中获得最大的收益。
  
  回复
Leo Jingbo 2020年4月17日下午7:16 #

感谢这篇精彩的帖子，非常有帮助。我有一个问题。如何检查多元时间序列的平稳性？我可以只测试标签吗？还是测试所有变量？

此致，
Leo

回复
- Jason Brownlee 2020年4月18日上午5:45 #
  
  也许可以先检查每个独立的序列是否平稳？
  
  回复
Hypnose 2020年4月21日下午3:15 #

嗨 Jason，好文章

我对我自己的数据集执行了您在文章中介绍的两种方法。

– 首先，我计算了通过滞后获得的许多子序列的均值，并计算了它们的方差，我对这些方差也做了同样的事情。我发现均值的方差和方差的方差都太大，因此根据平稳性的定义，我得出结论该序列是非平稳的

– 其次，我对同一序列进行了 ADF 检验，得到的 p 值低于临界值，然后我拒绝了原假设，该序列是平稳的

我用两种方法得到了两个不同的结论，请问出了什么问题？

抱歉我的英语不好，我是法国人。

回复
- Jason Brownlee 2020年4月22日上午5:48 #
  
  谢谢。
  
  也许可以尝试对数据进行差分，然后对差分后的数据拟合模型，再对原始数据拟合模型，并使用性能最好的模型。
  
  回复
  - Hypnose 2020年4月22日下午9:17 #
    
    谢谢。
    
    我会这么做的
    
    回复
Sai kumar 2020年6月7日下午10:50 #

你好 Jason，

我是机器学习的新手，您的文章对时间序列模型非常有帮助 🙂
您能帮我解决以下问题吗？

执行迪基-富勒检验后，我的结果是
ADF 统计量：-1.32
p 值：0.61

这清楚地表明我的模型是非平稳的，现在要使其平稳，下一步应该是什么？
我还想知道我的数据集只有两个变量：日期和销售值，我可以使用 ARIMA 模型还是其他模型？

提前感谢

回复
- Jason Brownlee 2020年6月8日上午6:13 #
  
  如果您有季节性，可以探索季节性差分；如果您有趋势，可以探索差分，如果您不确定，则使用后者。
  
  这可能会有所帮助
  https://machinelearning.org.cn/machine-learning-data-transforms-for-time-series-forecasting/
  
  回复
hossein Amini 2020年6月15日上午2:18 #

如何区分我们时间序列中平稳性的起始点？例如，我们已经知道我们的信号是平稳的，但是如何确定平稳的时间点？我首先想到的是将信号分成不同的部分，然后计算每个部分的统计量。通过找出显著差异，可以确定，但这不合逻辑，因为它不是一个自动的方法。
正确的想法是什么？

回复
- Jason Brownlee 2020年6月15日上午6:07 #
  
  抱歉，我不确定我是否理解。这个系列要么是平稳的，要么不是。
  
  回复
Vinod 2020年7月9日上午4:59 #

我是深度学习新手。我想知道如何使用 CNN 进行时间序列分类

回复
- Jason Brownlee 2020年7月9日上午6:44 #
  
  看这里
  https://machinelearning.org.cn/how-to-develop-convolutional-neural-network-models-for-time-series-forecasting/
  
  回复
Rahul Kumar 2020年10月9日上午12:02 #

在实现 dickey-fuller 检验 adfuller() 之前的一点修正

adfuller() 接受一维时间序列数组。
请将其更正为

X = X.iloc[:,0].values

因为它在处理二维数组时会报错。

回复
Saeed 2021年6月5日下午8:22 #

嗨，Jason，
一如既往，感谢您的精彩演示。

假设过程已经是平稳的（即 I(0) 并且 ADF 单位根检验被拒绝），是否还需要检查一阶差分？如果需要，其原理/应用是什么？

任何帮助不胜感激。

回复
- Jason Brownlee 2021年6月6日上午5:49 #
  
  如果您的数据在视觉和统计上都是平稳的，那么可能不需要进行差分。
  
  回复
Luigi 2021年7月23日下午11:43 #

嗨，Jason，
我正面临一种无法解释的行为。
我运行了 adfuller，t 统计量和 p 值表明我的序列是平稳的。
之后，我对我的信号 s 和信号平方（我想检查我是否有条件异方差性）都使用了 plot_acf 和 plot_pacf。
结果，图中显示 s 和 s**2 都存在高阶滞后，这对我来说意味着序列不平稳且异方差。
我错过了什么？acf 和 pacf 以及 adfueller 检验似乎是矛盾的。

谢谢
Luigi

回复
- Jason Brownlee 2021年7月24日上午5:15 #
  
  滞后相关不意味着非平稳。
  
  回复
Nathan Hanks 2021年8月6日上午9:12 #

关于缩放，您是在缩放数据之后还是之前应用差分变换？如果我只是应用 MinMaxScaler，它会重置到一个范围，趋势仍然会很明显，所以我想这无关紧要，但我想听听您的建议。

谢谢你。

回复
- Jason Brownlee 2021年8月7日上午5:36 #
  
  本教程将帮助您了解转换的顺序。
  https://machinelearning.org.cn/machine-learning-data-transforms-for-time-series-forecasting/
  
  回复
Rex 2021年11月7日下午4:28 #

你好，Jason。

这是一个很棒的教程，对我帮助很大。
只是一个快速问题。

应用对数变换后结果是否可能变得更糟？

这是对数变换前后的结果。

————————————————————————————————————————————
# 之前

ADF 统计量：-3.365537
p 值：0.012191
临界值
1%: -3.563
5%: -2.919
10%: -2.597
————————————————————————————————————————————
# 之后

ADF 统计量：-3.165451
p 值：0.022074
临界值
1%: -3.563
5%: -2.919
10%: -2.597

————————————————————————————————————————————
顺便说一句，我想和您分享我的经验。
在进行对数变换之前，我计算了原始数据的均值和方差。
这是结果

均值1=2046.769231，均值2=1811.777778
方差1=91577.384615，方差2=19364.641026

我以为它是非平稳的。
然而，ADF 检验表明，它在 5% 的显著性水平下是平稳的。
这令人惊讶且意义重大。下次我应该同时进行两次检查，哈哈哈。

回复
- Adrian Tam 2021年11月14日上午11:16 #
  
  对数变换是非线性的。因此，对于某些模型或数据集，它肯定会变得更糟。
  
  回复
Saleh 2022年3月19日下午9:55 #

嗨，Jason，

我正在处理一个非平稳时间序列。我认为这个时间序列可能是分段平稳的，这意味着在足够短的时间间隔内，它可能是平稳的。举例来说，语音信号就具有这种行为，这意味着尽管它在长时间间隔内不平稳，但可以在 20 毫秒的短时间间隔内被建模为平稳信号。

我想找出我正在处理的时间序列的这个短间隔的长度？您对此有什么建议吗？我只能通过试错来做吗？

假设我正在预测数据中心网络的流量演变，并且我有一些流量数据集。Arima 是我正在尝试的第一个模型，显然这个时间序列是非平稳的，它的统计数据随时间变化，但我猜测在短时间内它可以被认为是平稳的。我应该只取一个任意间隔并应用 ADF 检验吗？

回复
gng23 2023年5月19日下午11:37 #

谢谢，太棒了！

回复
- James Carmichael 2023年5月20日上午6:06 #
  
  谢谢 gng23 的反馈！我们很感激！
  
  回复

导航

如何使用 Python 检查时间序列数据是否平稳

平稳时间序列

停止以慢速学习时间序列预测！

非平稳时间序列

平稳时间序列的类型

平稳时间序列和预测

平稳性检查

描述性统计

每日出生人数数据集

航空公司乘客数据集

增广迪基-富勒检验

总结

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

最终将时间序列预测带入
您自己的项目

关于此主题的更多信息

对《如何使用Python检查时间序列数据是否平稳》的183条回复

发表评论点击此处取消回复。

导航

平稳时间序列

停止以**慢速**学习时间序列预测！

非平稳时间序列

平稳时间序列的类型

平稳时间序列和预测

平稳性检查

描述性统计

每日出生人数数据集

航空公司乘客数据集

增广迪基-富勒检验

总结

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

最终将时间序列预测带入您自己的项目

关于此主题的更多信息

对《如何使用Python检查时间序列数据是否平稳》的183条回复

发表评论 点击此处取消回复。

停止以慢速学习时间序列预测！

最终将时间序列预测带入
您自己的项目

发表评论点击此处取消回复。