Python时间序列预测案例研究：波士顿月度武装抢劫案

时间序列预测是一个过程，要想获得良好的预测，唯一的方法就是实践这个过程。

在本教程中，您将学习如何使用Python预测波士顿月度武装抢劫案的数量。

完成本教程将为您提供一个框架，用于处理您自己的时间序列预测问题，并掌握相应的步骤和工具。

完成本教程后，您将了解：

• 如何检查您的Python环境并仔细定义时间序列预测问题。
• 如何创建评估模型的测试平台，开发一个基准预测，并通过时间序列分析工具更好地理解您的问题。
• 如何开发一个自回归积分移动平均模型，将其保存到文件，并在以后加载它以对新的时间步长进行预测。

通过我的新书 《Python时间序列预测入门》 启动您的项目，书中包含分步教程和所有示例的Python源代码文件。

让我们开始吧。

• 更新于2018年7月：修复了ACF/PACF图准备中的一个拼写错误（感谢Patrick Wolf）。
• 2019 年 4 月更新：更新了数据集链接。
• 2019年8月更新：更新了数据加载以使用新的API。
• 更新于2020年2月：更新了to_csv()以消除警告。
• **2020 年 12 月更新**：针对 API 更改更新了建模。

Python时间序列预测案例研究——波士顿月度武装抢劫案
摄影：Tim Sackton，部分权利保留。

概述

在本教程中，我们将端到端地完成一个时间序列预测项目，从下载数据集和定义问题到训练最终模型和进行预测。

这个项目并非详尽无遗，但它展示了如何通过系统地解决一个时间序列预测问题来快速获得良好结果。

我们将要完成的本项目的步骤如下：

1. 环境。
2. 问题描述。
3. 测试平台。
4. 持久性。
5. 数据分析。
6. ARIMA模型
7. 模型验证

这将为解决时间序列预测问题提供一个模板，您可以将其用于您自己的数据集。

1. 环境

本教程假定已安装并运行SciPy环境及相关依赖项，包括：

• SciPy
• NumPy
• Matplotlib
• Pandas
• scikit-learn
• statsmodels

我使用的是Python 2.7。您使用的是Python 3吗？请在评论区告诉我您的经验。

此脚本将帮助您检查这些库的已安装版本。

在编写本教程的工作站上，我的结果如下：

2. 问题描述

问题是预测美国波士顿月度武装抢劫案的数量。

该数据集提供了1966年1月至1975年10月，即不到10年的波士顿月度武装抢劫案数量。

数值为计数，有118个观测值。

该数据集归功于McCleary & Hay (1980)。

• 下载数据集.

下载数据集为CSV文件，并将其放入当前工作目录，文件名为“robberies.csv”。

3. 测试平台

我们必须开发一个测试平台来研究数据和评估候选模型。

这涉及两个步骤

1. 定义验证数据集。
2. 开发模型评估方法。

3.1 验证数据集

该数据集不是最新的。这意味着我们无法轻易收集更新的数据来验证模型。

因此，我们将假装是1974年10月，并将最后一年的数据保留起来用于分析和模型选择。

最后一年数据将用于验证最终模型。

下面的代码将加载数据集为一个Pandas Series，并将其分为两部分：一部分用于模型开发（dataset.csv），另一部分用于验证（validation.csv）。

运行该示例会创建两个文件，并打印出每个文件中的观测数量。

这些文件的具体内容是：

• dataset.csv：从1966年1月到1974年10月的观测值（106个观测值）
• validation.csv：从1974年11月到1975年10月的观测值（12个观测值）

验证数据集占原始数据集的10%。

请注意，保存的数据集不包含标题行，因此我们以后在处理这些文件时无需考虑这一点。

3.2. 模型评估

模型评估仅在上一节准备的dataset.csv文件中进行。

模型评估包括两个要素：

1. 性能度量。
2. 测试策略。

3.2.1 性能度量

观测值是抢劫案的数量。

我们将使用均方根误差（RMSE）来评估预测的性能。这将为严重错误的预测提供更高的权重，并且其单位与原始数据相同。

在计算和报告RMSE之前，必须撤销对数据进行的任何转换，以便不同方法之间的性能可以直接进行比较。

我们可以使用scikit-learn库中的帮助函数mean_squared_error()来计算RMSE，该函数计算预期值列表（测试集）和预测值列表之间的平均平方误差。然后，我们可以取该值的平方根，得到RMSE分数。

例如

3.2.2 测试策略

候选模型将使用前向验证进行评估。

这是因为问题定义要求使用滚动预测类型的模型。在这种情况下，需要根据所有可用数据进行一步预测。

前向验证将按以下方式工作：

• 数据集的前50%将保留用于训练模型。
• 剩余50%的数据集将被迭代并用于测试模型。
• 对于测试数据集中的每一步：
  • 将训练一个模型。
  • 进行一步预测，并将预测存储起来以供以后评估。
  • 测试数据集中实际的观测值将在下一次迭代中添加到训练数据集中。
• 在测试数据集迭代过程中进行的预测将被评估，并报告RMSE分数。

鉴于数据量较小，我们将允许模型在每次预测之前使用所有可用数据进行重新训练。

我们可以使用简单的NumPy和Python代码来编写测试平台的代码。

首先，我们可以直接将数据集分割成训练集和测试集。我们小心地将加载的数据集始终转换为float32，以防加载的数据仍然具有某些字符串或整数数据类型。

接下来，我们可以迭代测试数据集中的时间步长。训练数据集存储在Python列表中，因为我们需要在每次迭代中轻松地追加一个新观测值，而NumPy数组拼接感觉有些过度。

模型进行的预测根据惯例称为yhat，因为结果或观测值被称为y，而yhat（一个带有标记的“y”）是变量y预测的数学表示。

每次观测值都会打印预测值和观测值，以便在模型存在问题时进行健全性检查预测。

4. 持久性

在深入进行数据分析和建模之前，第一步是建立一个性能基准。

这将为使用提出的测试平台评估模型提供一个模板，并为所有更复杂的预测模型提供一个性能比较基准。

时间序列预测的基准预测称为朴素预测，或持久性预测。

这是将前一个时间步长的观测值用作下一个时间步长观测值的预测。

我们可以将其直接插入上一节定义的测试平台。

完整的代码列表如下。

运行测试平台会打印测试数据集每次迭代的预测值和观测值。

示例最后会打印模型的RMSE。

在这种情况下，我们可以看到持久性模型达到了51.844的RMSE。这意味着平均而言，该模型在每次预测时都偏离了大约51个抢劫案。

我们现在有了基准预测方法和性能；现在我们可以开始深入挖掘我们的数据了。

5. 数据分析

我们可以使用汇总统计数据和数据图表来快速了解预测问题的结构。

在本节中，我们将从四个角度审视数据：

1. 汇总统计。
2. 折线图。
3. 密度图。
4. 箱线图。

5.1 汇总统计。

在文本编辑器中打开数据dataset.csv文件或原始robberies.csv文件，查看数据。

快速检查表明没有明显的缺失观测值。如果我们尝试强制将值转换为浮点数，并且数据中存在NaN或“?”之类的值，我们可能早就注意到了。

汇总统计数据可以快速了解观测值的范围。它可以帮助我们快速了解我们正在处理的数据。

下面的示例计算并打印时间序列的汇总统计数据。

运行该示例会提供一系列汇总统计数据供您查看。

从这些统计数据中可以观察到：

• 观测数量（count）与我们的预期相符，这意味着我们正确地处理了数据。
• 平均值约为173，我们可以将其视为该序列的水平。
• 标准差（平均值与均值的偏差）相对较大，为112起抢劫案。
• 百分位数以及标准差确实表明数据的范围很大。

如果这种大的数据范围是由于随机波动（例如非系统性）引起的，那么要实现非常准确的预测可能会很困难。

5.2 折线图

时间序列的折线图可以为问题提供很多见解。

下面的示例创建并显示了数据集的折线图。

运行示例并查看图表。注意序列中任何明显的时序结构。

从图表中可以观察到：

• 随着时间的推移，抢劫案有增加的趋势。
• 似乎没有明显的异常值。
• 年复一年的波动相对较大，有升有降。
• 后期年份的波动似乎比早期年份的波动更大。
• 这种趋势意味着数据集几乎肯定是非平稳的，而波动的变化也可能加剧这种情况。

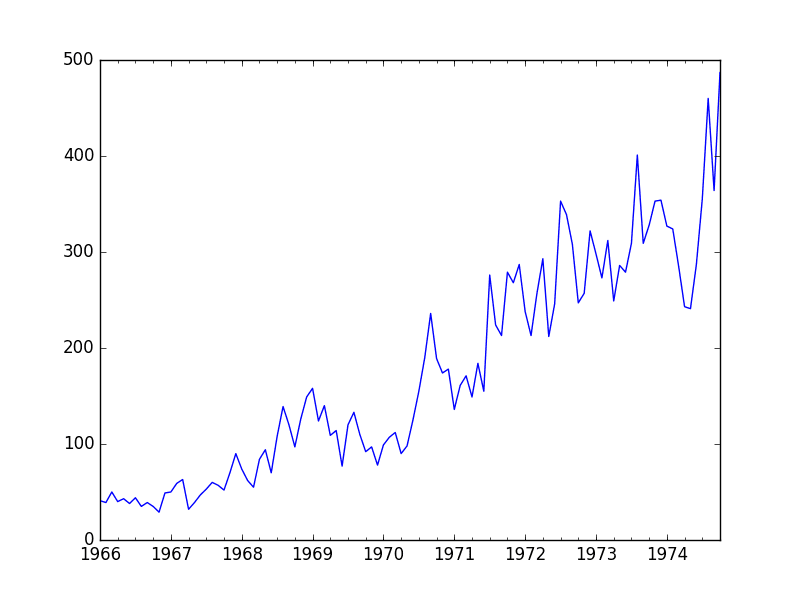
波士顿月度抢劫案折线图

这些简单的观察表明，我们可能会从对趋势进行建模并从中移除时间序列中获益。

或者，我们可以使用差分使序列平稳以便建模。如果后期年份的波动存在增长趋势，我们甚至可能需要进行两级差分。

5.3 密度图

审视观测值密度图可以为数据结构提供进一步的见解。

下面的示例创建了观测值的直方图和密度图，而不考虑任何时间结构。

运行示例并查看图表。

从图表中可以观察到：

• 分布不是高斯分布。
• 分布是左偏的，可能是指数分布或双高斯分布。

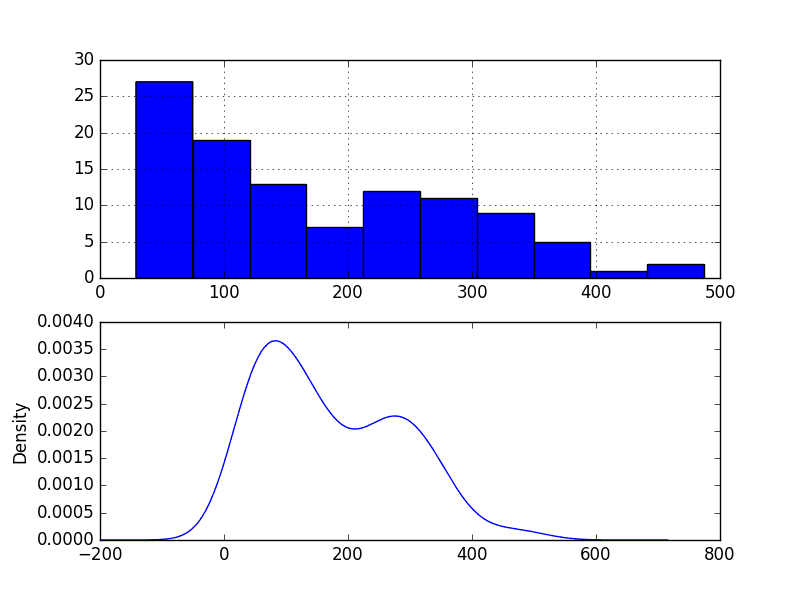
波士顿月度抢劫案密度图

我们可能会从在建模之前探索数据的某些幂变换中获益。

5.4 箱线图

我们可以按年份对月度数据进行分组，并了解每年的观测值范围以及这种范围如何变化。

我们预计会看到一些趋势（均值或中位数增加），但查看分布的其余部分如何变化可能会很有趣。

下面的示例按年份对观测值进行分组，并为每年的观测值创建一个箱线图。最后一年（1974年）只有10个月，可能与其他年份的12个月观测值没有可比性。因此，只绘制了1966年至1973年的数据。

运行该示例会创建8个并排的箱线图，每个图代表选定数据的8年中的一年。

从审查图表中可以观察到：

• 每年的中位数（红线）显示出可能不是线性的趋势。
• 数据的范围，或中间50%（蓝框），有所不同，但可能随时间不一致。
• 早期年份，可能前两年，与其余数据集有很大不同。

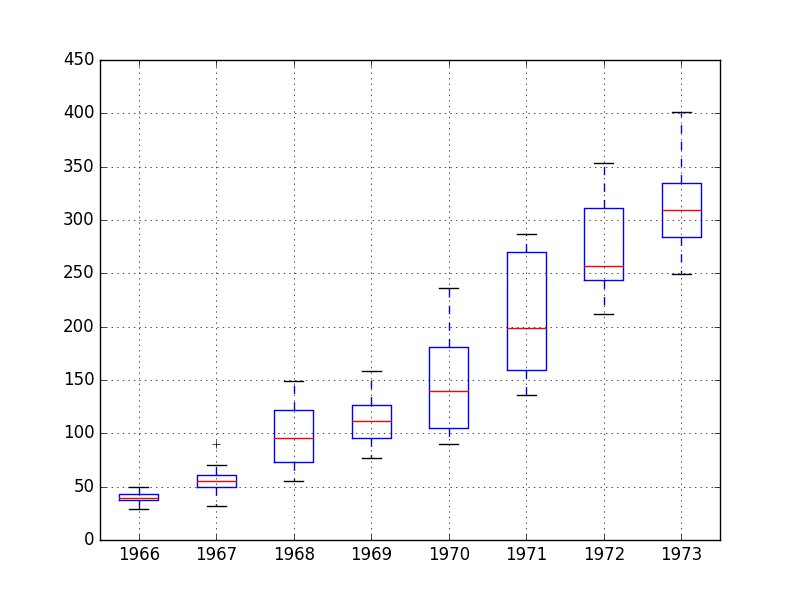
波士顿月度抢劫案箱线图

这些观察表明，年复一年的波动可能不是系统性的，难以建模。它们还表明，如果早期两年数据确实非常不同，那么在建模时可能需要将其剔除。

这种年度数据视图是一个有趣的途径，可以通过查看逐年的汇总统计数据以及年度汇总统计数据的变化来进一步深入研究。

接下来，我们可以开始研究该序列的预测模型。

6. ARIMA模型

在本节中，我们将为该问题开发自回归积分移动平均（ARIMA）模型。

我们将分四个步骤进行：

1. 开发手动配置的ARIMA模型。
2. 使用ARIMA网格搜索寻找优化模型。
3. 分析预测残差误差以评估模型的任何偏差。
4. 通过幂变换探索模型改进。

6.1 手动配置ARIMA

非季节性ARIMA(p,d,q)需要三个参数，并且传统上是手动配置的。

时间序列数据的分析假设我们处理的是平稳时间序列。

该时间序列几乎肯定是非平稳的。我们可以通过首先对序列进行差分并使用统计检验来确认结果是平稳的，从而使其平稳。

下面的示例创建了该序列的平稳版本，并将其保存到文件stationary.csv。

运行示例将输出一个统计显著性检验的结果，该检验用于确定序列是否是平稳的。具体来说，是增广迪基-福勒检验。

结果显示，检验统计量值为 -3.980946，小于 5% 临界值 -2.893。这表明我们可以在 5% 的显著性水平下拒绝原假设（即结果是统计巧合的概率很低）。

拒绝零假设意味着该过程没有单位根，进而意味着时间序列是平稳的或不具有时间相关结构。

这表明至少需要一个差分阶数。我们 ARIMA 模型中的 *d* 参数至少应为 1。

下一步是为自回归（AR）和移动平均（MA）参数 p 和 q 选择滞后值。

我们可以通过查看自相关函数（ACF）和偏自相关函数（PACF）图来做到这一点。

下面的示例为序列生成了 ACF 和 PACF 图。

运行示例并查看图表，以了解如何为 ARIMA 模型设置 p 和 q 变量。

以下是图表中的一些观察结果。

• ACF 显示 1 个月有显著滞后。
• PACF 显示大约 2 个月有显著滞后，并且在长达大约 12 个月的时间里滞后点零星出现。
• ACF 和 PACF 都在同一点下降，这可能表明 AR 和 MA 的混合。

p 和 q 值的良好起点是 1 或 2。

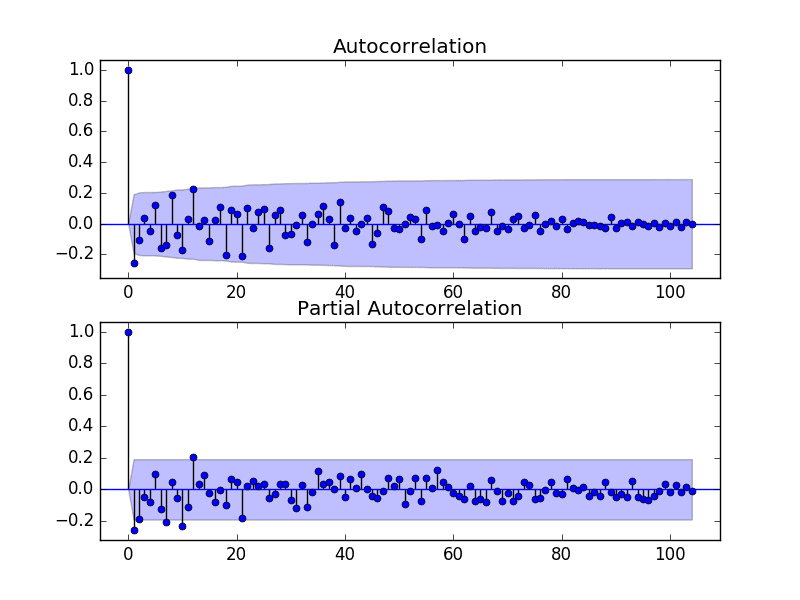
波士顿月度抢劫案 ACF 和 PACF 图

这个快速分析表明，在原始数据上使用 ARIMA(1,1,2) 可能是一个好的起点。

实验表明，这种 ARIMA 配置无法收敛，并导致底层库出现错误。一些实验表明，该模型似乎不稳定，同时定义了非零的 AR 和 MA 阶数。

该模型可以简化为 ARIMA(0,1,2)。下面的示例演示了此 ARIMA 模型在测试框架上的性能。

运行此示例将产生 49.821 的 RMSE，这低于持久性模型。

这是一个好的开始，但我们可能可以通过更好的 ARIMA 模型配置来获得改进的结果。

6.2 网格搜索 ARIMA 超参数

许多 ARIMA 配置在此数据集上不稳定，但可能存在其他超参数可以产生性能良好的模型。

在本节中，我们将搜索 p、d 和 q 的值，找出不导致错误的组合，并找到产生最佳性能的组合。我们将使用网格搜索来探索子集整数值中的所有组合。

具体来说，我们将搜索以下参数的所有组合

• p：0 到 12。
• d：0 到 3。
• q：0 到 12。

这是 (13 * 4 * 13)，即 676 次测试框架运行，在现代硬件上执行需要一些时间。

带有网格搜索版本测试框架的完整示例代码如下所示。

运行示例将遍历所有组合，并报告收敛且无错误的组合结果。

该示例在现代硬件上运行大约需要不到 2 个小时。

结果显示，发现的最佳配置是 ARIMA(0, 1, 2)；巧合的是，这在上一节中已经演示过。

6.3 检查残差误差

对模型进行良好最终检查是检查残差预测误差。

理想情况下，残差误差的分布应为零均值的正态分布。

我们可以通过绘制残差的直方图和密度图来检查这一点。

下面的示例计算测试集上的预测的残差误差，并创建这些密度图。

运行示例创建了两个图。

图表显示了类似正态的分布，但右尾较长。

这可能表明预测存在偏差，在这种情况下，在建模之前对原始数据进行基于幂的转换可能是有用的。

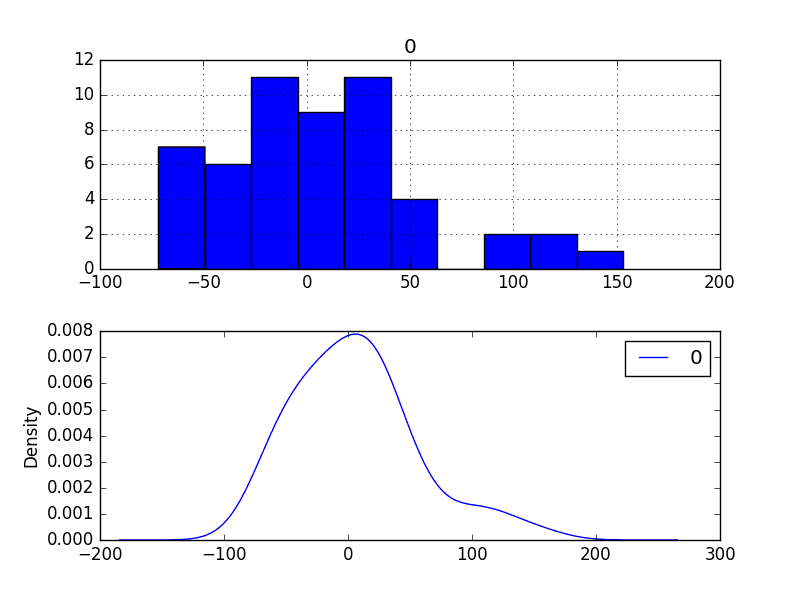
残差误差密度图

检查残差误差时间序列是否存在任何类型的自相关也是一个好主意。如果存在，则表明模型有更多机会对数据中的时间结构进行建模。

下面的示例重新计算残差误差，并创建 ACF 和 PACF 图以检查任何显著的自相关。

结果表明，时间序列中存在的少量自相关已被模型捕获。

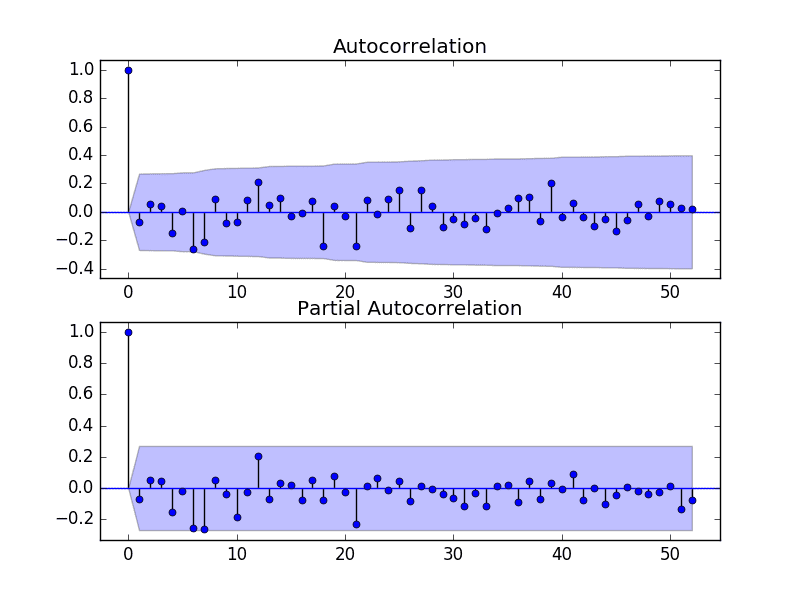
残差误差 ACF 和 PACF 图

6.4 Box-Cox 变换数据集

Box-Cox 变换是一种能够评估一系列幂变换的方法，包括但不限于对数据进行对数、平方根和倒数变换。

下面的示例执行对数据的对数变换，并生成一些图来查看对时间序列的影响。

运行示例将创建三个图：转换后的时间序列的折线图、显示转换后值分布的直方图以及显示值分布与理想高斯分布比较的 Q-Q 图。

这些图中的一些观察结果如下：

• 时间序列的折线图中已移除大幅波动。
• 直方图显示了更平坦或更均匀（表现良好）的值分布。
• Q-Q 图尚可，但仍未完全符合高斯分布。

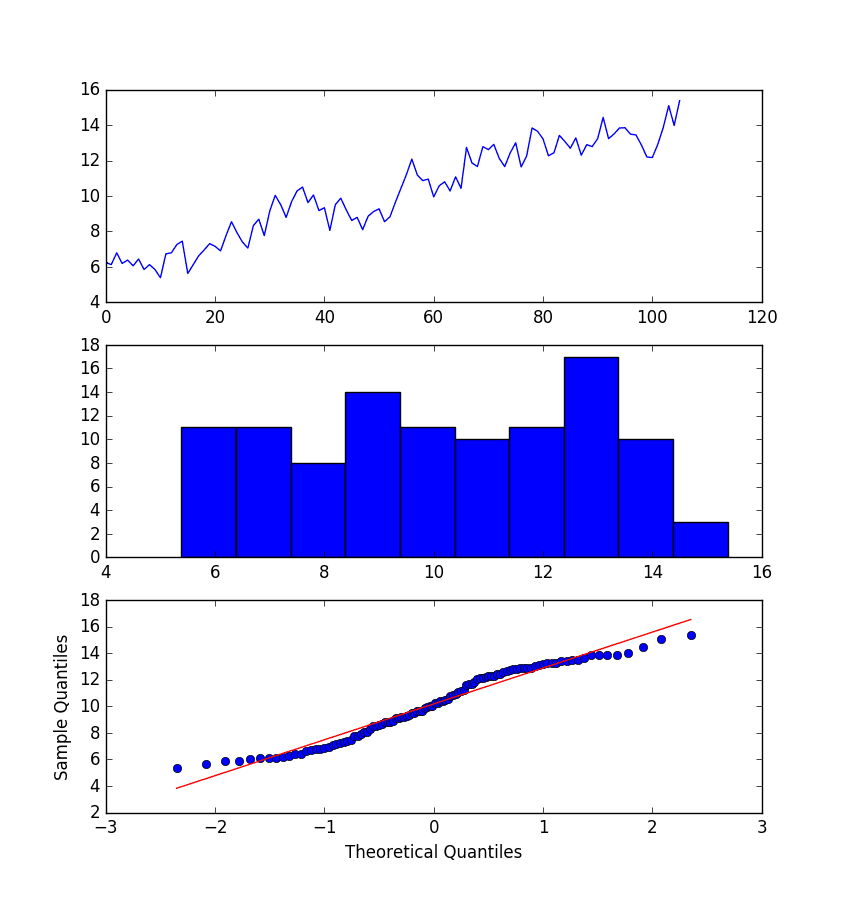
BoxCox 变换的月度波士顿抢劫案图

毫无疑问，Box-Cox 变换对时间序列产生了一定的影响，并且可能有用。

在继续使用变换后的数据测试 ARIMA 模型之前，我们必须有一种方法来反转变换，以便将使用在变换数据上训练的模型所做的预测转换回原始尺度。

示例中使用的 `boxcox()` 函数通过优化成本函数来查找理想的 lambda 值。

Lambda 用于以下函数来变换数据：

此变换函数可以直接反转，如下所示：

此逆 Box-Cox 变换函数可以在 Python 中实现如下：

我们可以用 Box-Cox 变换重新评估 ARIMA(0,1,2) 模型。

这包括在拟合 ARIMA 模型之前先转换历史数据，然后对预测进行变换反转，再将其存储起来以便稍后与预期值进行比较。

`boxcox()` 函数可能会失败。在实践中，我遇到过这种情况，它似乎是通过返回小于 -5 的 lambda 值来指示的。按照惯例，lambda 值在 -5 到 5 之间进行评估。

会添加一个检查，以防 lambda 值小于 -5。如果发生这种情况，则假定 lambda 值为 1，并使用原始历史数据来拟合模型。lambda 值为 1 等同于“无变换”，因此逆变换不起作用。

完整的示例如下所示。

运行示例将打印每次迭代的预测值和预期值。

注意，您可能会看到使用 boxcox() 变换函数时出现警告；例如：

这些现在可以忽略。

变换后数据上的模型最终 RMSE 为 49.443。这比未变换数据的 ARIMA 模型误差要小，但仅略微减小，可能在统计上不显著。

我们将使用带有 Box-Cox 变换的模型作为最终模型。

7. 模型验证

在模型开发和选定最终模型后，必须对其进行验证和定稿。

验证是过程的可选部分，但它提供了“最后一次检查”，以确保我们没有欺骗自己。

本节包括以下步骤：

1. 最终确定模型：训练并保存最终模型。
2. 进行预测：加载已定型的模型并进行预测。
3. 验证模型：加载并验证最终模型。

7.1 最终确定模型

最终确定模型涉及在整个数据集上拟合 ARIMA 模型，在本例中，是在整个数据集的变换版本上进行拟合。

拟合后，可以将模型保存到文件中以供将来使用。由于还对数据进行了 Box-Cox 变换，因此我们需要知道所选的 lambda 值，以便将模型预测转换回原始、未变换的尺度。

下面的示例在 Box-Cox 变换数据集上拟合 ARIMA(0,1,2) 模型，并将整个拟合对象和 lambda 值保存到文件中。

运行示例将创建两个本地文件：

• model.pkl 这是 `ARIMA.fit()` 调用返回的 ARIMAResult 对象。它包括系数和拟合模型时返回的所有其他内部数据。
• model_lambda.npy 这是存储为单行单列 NumPy 数组的 lambda 值。

这可能有点矫枉过正，而且对于实际应用来说，真正需要的是模型中的 AR 和 MA 系数、差分次数的 d 参数，或许还有滞后观测值和模型残差，以及用于变换的 lambda 值。

7.2 进行预测

一个自然的需求可能是加载模型并进行单次预测。

这相对直接，包括恢复保存的模型和 lambda 值，并调用 forecast() 方法。

下面的示例加载模型，对下一个时间步进行预测，对 Box-Cox 变换进行逆变换，并打印预测结果。

运行示例将打印出约 452 的预测值。

如果我们查看 validation.csv，可以看到下一时间段的第一行的值为 452。模型 100% 准确，这令人印象深刻（或幸运）。

7.3 验证模型

我们可以加载模型并以模拟的实际操作方式来使用它。

在测试框架部分，我们将原始数据集的最后 12 个月保存在一个单独的文件中，以验证最终模型。

我们现在可以加载这个 validation.csv 文件，并用它来查看我们的模型在“未见过”的数据上的表现。

我们有两种可能的方法：

• 加载模型并使用它来预测未来 12 个月。超过前一两个月的预测会很快开始失去准确性。
• 加载模型并以滚动预测的方式使用它，为每个时间步更新变换和模型。这是首选方法，因为它也是人们在实践中将如何使用此模型，并且能实现最佳性能。

与前面几节中的模型评估一样，我们将以滚动预测的方式进行预测。这意味着我们将遍历验证数据集中的提前期，并将观测值作为历史的更新。

运行示例将打印出验证数据集中时间步长的每个预测值和期望值。

验证期的最终 RMSE 预测为 53 起抢劫案。这与预期的误差 49 起相差不大，但我认为这与简单的持续性模型相比也相差不大。

同时还提供了预测与验证数据集的比较图。

该预测具有持续性预测的特征。这确实表明，尽管该时间序列有明显的趋势，但它仍然是一个相当困难的问题。

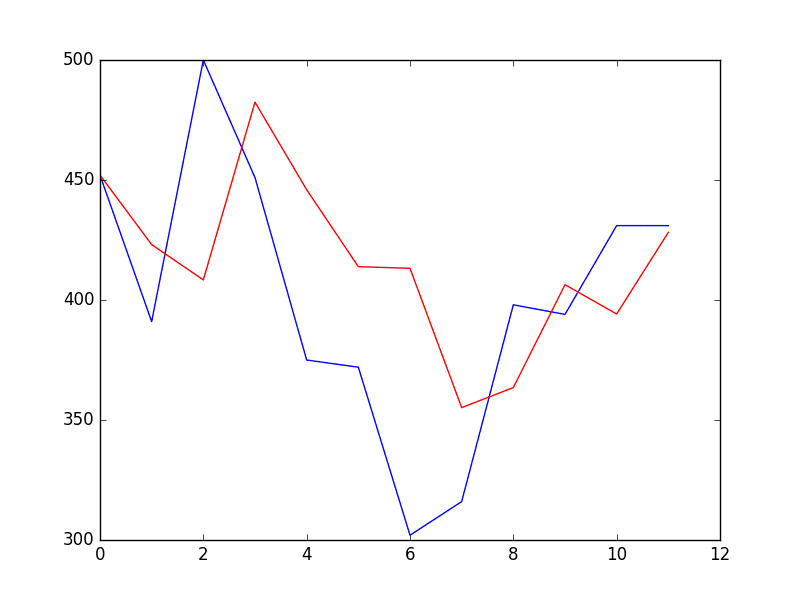
验证时间步长的预测

教程扩展

本教程并不详尽，可能还有更多可以改进结果的方法。

本节列出了一些想法。

• 统计显著性检验。使用统计检验来检查不同模型结果之间的差异是否具有统计学意义。学生 t 检验将是一个不错的起点。
• 带数据变换的网格搜索。在 ARIMA 超参数中重复网格搜索，并使用 Box-Cox 变换，看看是否可以获得不同且更好的参数集。
• 检查残差。调查带 Box-Cox 变换的最终模型的残差预测误差，看看是否存在可以解决的进一步偏差和/或自相关。
• 精简模型保存。简化模型保存，仅存储所需的系数，而不是整个 ARIMAResults 对象。
• 手动处理趋势。直接使用线性或非线性模型对趋势进行建模，并将其显式地从序列中移除。如果趋势是非线性的并且可以比线性情况更好地建模，这可能会带来更好的性能。
• 置信区间。在验证数据集上显示预测的置信区间。
• 数据选择。考虑在不使用前两年数据的情况下对问题进行建模，看看这对预测技能有何影响。

您是否实现了这些扩展中的任何一个？您是否能够获得更好的结果？
在下面的评论中分享您的发现。

总结

在本教程中，您发现了使用 Python 进行时间序列预测项目的步骤和工具。

本教程涵盖了很多内容，特别是

• 如何开发具有性能度量和评估方法的测试框架，以及如何快速开发基线预测和技能。
• 如何使用时间序列分析来提出关于如何最佳地对预测问题进行建模的想法。
• 如何开发 ARIMA 模型、保存它，然后稍后加载它以对新数据进行预测。

您做得怎么样？您对本教程有任何疑问吗？
在下面的评论中提出你的问题，我会尽力回答。

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

...只需几行python代码

在我的新电子书中探索如何实现
Python 时间序列预测入门

它涵盖了**自学教程**和**端到端项目**，主题包括：*数据加载、可视化、建模、算法调优*等等。

最终将时间序列预测带入
您自己的项目

跳过学术理论。只看结果。

查看内容