Python 时间序列预测研究：法国香槟月销售额

时间序列预测是一个过程，要想获得良好的预测，唯一的方法就是实践这个过程。

在本教程中，您将学习如何使用 Python 预测法国香槟的月度销量。

完成本教程将为您提供一个框架，用于处理您自己的时间序列预测问题，并掌握相应的步骤和工具。

完成本教程后，您将了解：

• 如何确认您的 Python 环境并仔细定义时间序列预测问题。
• 如何创建评估模型的测试平台，开发一个基准预测，并通过时间序列分析工具更好地理解您的问题。
• 如何开发一个自回归积分移动平均模型，将其保存到文件，并在以后加载它以对新的时间步长进行预测。

我的新书《使用 Python 进行时间序列预测》包含分步教程和所有示例的 Python 源代码文件，助您启动项目。

让我们开始吧。

• 2017 年 3 月更新：修复了代码示例中的一个错别字。
• 2019 年 4 月更新：更新了数据集链接。
• 2019 年 8 月更新：更新了数据加载和日期分组以使用新的 API。
• 更新于2020年2月：更新了to_csv()以消除警告。
• 2020 年 2 月更新：修复了数据准备和加载问题。
• 2020 年 5 月更新：修复了进行预测时的一个小错别字。
• **2020 年 12 月更新**：针对 API 更改更新了建模。

使用 Python 进行时间序列预测研究 – 法国香槟的月度销量
图片由 Basheer Tome 提供，部分权利保留。

概述

在本教程中，我们将端到端地完成一个时间序列预测项目，从下载数据集和定义问题到训练最终模型和进行预测。

这个项目并非详尽无遗，但它展示了如何通过系统地解决一个时间序列预测问题来快速获得良好结果。

我们将通过的项目步骤如下：

1. 环境。
2. 问题描述。
3. 测试平台。
4. 持久性。
5. 数据分析。
6. ARIMA 模型。
7. 模型验证。

这将为解决时间序列预测问题提供一个模板，您可以将其用于您自己的数据集。

1. 环境

本教程假定已安装并运行SciPy环境及相关依赖项，包括：

• SciPy
• NumPy
• Matplotlib
• Pandas
• scikit-learn
• statsmodels

如果您需要帮助在工作站上安装 Python 和 SciPy 环境，请考虑 Anaconda 发行版，它可以为您处理大部分工作。

此脚本将帮助您检查这些库的已安装版本。

在编写本教程的工作站上，我的结果如下：

2. 问题描述

问题是预测 Perrin Freres 品牌（以法国一个地区命名）香槟的月度销量。

数据集提供了从 1964 年 1 月到 1972 年 9 月的香槟月度销量，即不到 10 年的数据。

这些值是百万销量的计数，共有 105 个观测值。

该数据集归功于 Makridakis 和 Wheelwright，1989 年。

• 下载数据集.

将数据集下载为 CSV 文件并将其放置在当前工作目录中，文件名为“champagne.csv”。

3. 测试平台

我们必须开发一个测试平台来研究数据和评估候选模型。

这涉及两个步骤

1. 定义验证数据集。
2. 开发模型评估方法。

3.1 验证数据集

该数据集不是最新的。这意味着我们无法轻易收集更新的数据来验证模型。

因此，我们将假定现在是 1971 年 9 月，并保留最后一年数据不进行分析和模型选择。

这一年的数据将用于验证最终模型。

下面的代码将加载数据集为一个Pandas Series，并将其分为两部分：一部分用于模型开发（dataset.csv），另一部分用于验证（validation.csv）。

运行该示例会创建两个文件，并打印出每个文件中的观测数量。

这些文件的具体内容是：

• dataset.csv：1964 年 1 月至 1971 年 9 月的观测值（93 个观测值）
• validation.csv：1971 年 10 月至 1972 年 9 月的观测值（12 个观测值）

验证数据集约占原始数据集的 11%。

请注意，保存的数据集没有标题行，因此我们稍后处理这些文件时无需考虑这一点。

3.2. 模型评估

模型评估仅在上一节准备的dataset.csv文件中进行。

模型评估包括两个要素：

1. 性能度量。
2. 测试策略。

3.2.1 性能度量

观测值是香槟销量的计数，单位为百万瓶。

我们将使用均方根误差（RMSE）来评估预测的性能。这将为严重错误的预测提供更高的权重，并且其单位与原始数据相同。

在计算和报告RMSE之前，必须撤销对数据进行的任何转换，以便不同方法之间的性能可以直接进行比较。

我们可以使用 scikit-learn 库中的辅助函数 mean_squared_error() 计算 RMSE，该函数计算预期值列表（测试集）和预测列表之间的均方误差。然后，我们可以取该值的平方根，得到 RMSE 分数。

例如

3.2.2 测试策略

候选模型将使用前向验证进行评估。

这是因为问题定义要求使用滚动预测类型的模型。在这种情况下，需要根据所有可用数据进行一步预测。

前向验证将按以下方式工作：

• 数据集的前50%将保留用于训练模型。
• 剩余50%的数据集将被迭代并用于测试模型。
• 对于测试数据集中的每一步：
  • 将训练一个模型。
  • 进行一步预测，并将预测存储起来以供以后评估。
  • 测试数据集中实际的观测值将在下一次迭代中添加到训练数据集中。
• 在测试数据集迭代期间进行的预测将被评估并报告 RMSE 分数。

鉴于数据量较小，我们将允许模型在每次预测之前使用所有可用数据进行重新训练。

我们可以使用简单的NumPy和Python代码来编写测试平台的代码。

首先，我们可以直接将数据集拆分为训练集和测试集。我们总是小心地将加载的数据集转换为 float32，以防加载的数据仍包含一些 String 或 Integer 数据类型。

接下来，我们可以遍历测试数据集中的时间步长。训练数据集存储在 Python 列表中，因为我们需要在每次迭代时轻松附加新的观测值，而 NumPy 数组连接似乎有点多余。

模型做出的预测根据惯例称为 yhat，因为结果或观测值称为 y，而 yhat（带帽子的“y”）是 y 变量预测的数学符号。

每次观测值都会打印预测值和观测值，以便在模型存在问题时进行健全性检查预测。

4. 持久性

在深入进行数据分析和建模之前，第一步是建立一个性能基准。

这将为使用提出的测试平台评估模型提供一个模板，并为所有更复杂的预测模型提供一个性能比较基准。

时间序列预测的基准预测称为朴素预测，或持久性预测。

这是将前一个时间步长的观测值用作下一个时间步长观测值的预测。

我们可以将其直接插入上一节定义的测试平台。

完整的代码列表如下。

运行测试平台会打印测试数据集每次迭代的预测值和观测值。

示例最后会打印模型的RMSE。

在这种情况下，我们可以看到持久性模型实现了 3186.501 的 RMSE。这意味着平均而言，模型在每次预测中都存在约 3186 百万销量的误差。

我们现在有了基准预测方法和性能；现在我们可以开始深入挖掘我们的数据了。

5. 数据分析

我们可以使用汇总统计数据和数据图表来快速了解预测问题的结构。

在本节中，我们将从五个角度审视数据

1. 汇总统计。
2. 折线图。
3. 季节性线图
4. 密度图。
5. 箱线图。

5.1 汇总统计

汇总统计数据可以快速了解观测值的范围。它可以帮助我们快速了解我们正在处理的数据。

下面的示例计算并打印时间序列的汇总统计数据。

运行该示例会提供一系列汇总统计数据供您查看。

从这些统计数据中可以观察到：

• 观测数量（count）与我们的预期相符，这意味着我们正确地处理了数据。
• 平均值约为 4641，我们可能将其视为该序列的水平值。
• 标准差（与平均值的平均差）相对较大，为 2486 销量。
• 百分位数和标准差确实表明数据分布范围很大。

5.2 线图

时间序列的线图可以提供对问题的大量洞察。

下面的示例创建并显示了数据集的折线图。

运行示例并查看图表。注意序列中任何明显的时序结构。

从图表中可以观察到：

• 销量可能随时间呈增长趋势。
• 每年的销量似乎都有系统性的季节性。
• 季节性信号似乎随时间增长，表明存在乘法关系（变化增加）。
• 似乎没有明显的异常值。
• 季节性表明该序列几乎肯定是非平稳的。

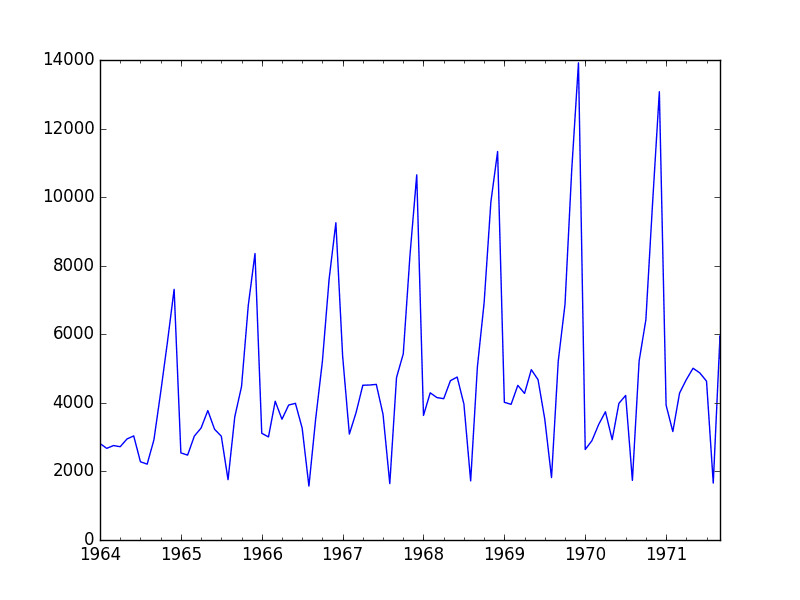
香槟销量线图

明确地对季节性成分建模并将其移除可能会有好处。您也可以探索使用一或两级的差分以使序列平稳。

季节性成分的增长趋势可能暗示使用对数或其他幂变换。

5.3 季节性线图

我们可以通过目视检查按年份划分的数据集的线图来确认季节性是年度循环的假设。

下面的示例将 7 年的完整数据作为单独的组，并为每个组创建一个线图。线图垂直对齐，以帮助发现任何逐年模式。

运行示例会创建 7 个线图堆栈。

我们可以清楚地看到每年八月销量下降，然后从八月到十二月销量上升。这种模式每年都相同，尽管水平不同。

这将有助于以后进行任何明确基于季节的建模。

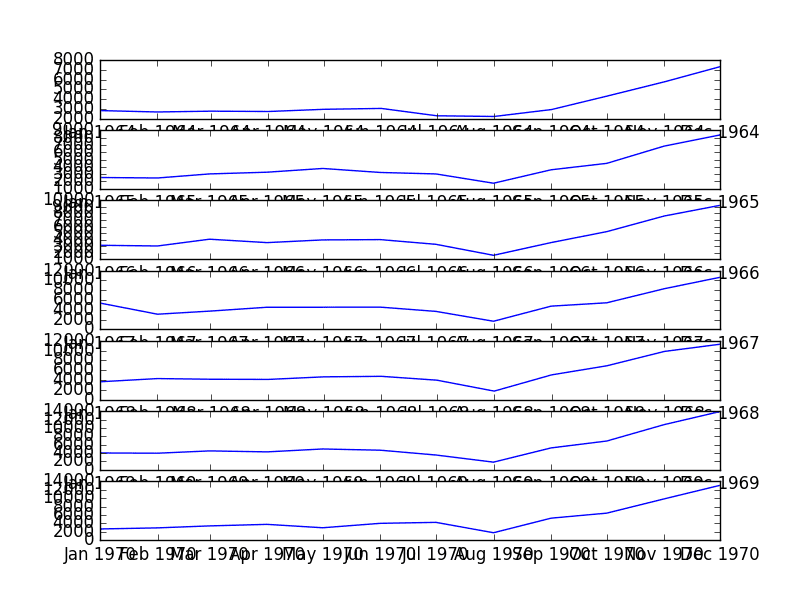
每年季节性线图

如果所有季节线图都添加到同一个图表中，可能更容易对比每年的数据。

5.4 密度图

审视观测值密度图可以为数据结构提供进一步的见解。

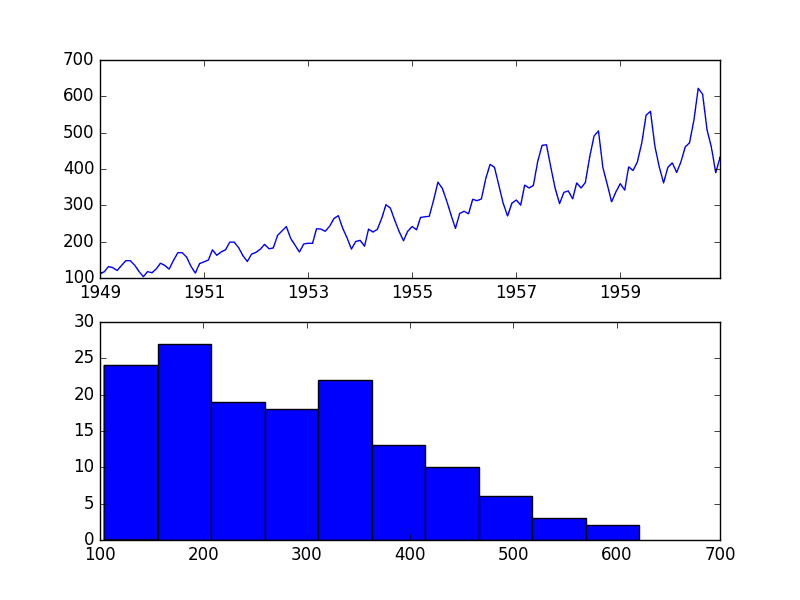
下面的示例创建了观测值的直方图和密度图，而不考虑任何时间结构。

运行示例并查看图表。

从图表中可以观察到：

• 分布不是高斯分布。
• 该形状具有长右尾，可能表明是指数分布

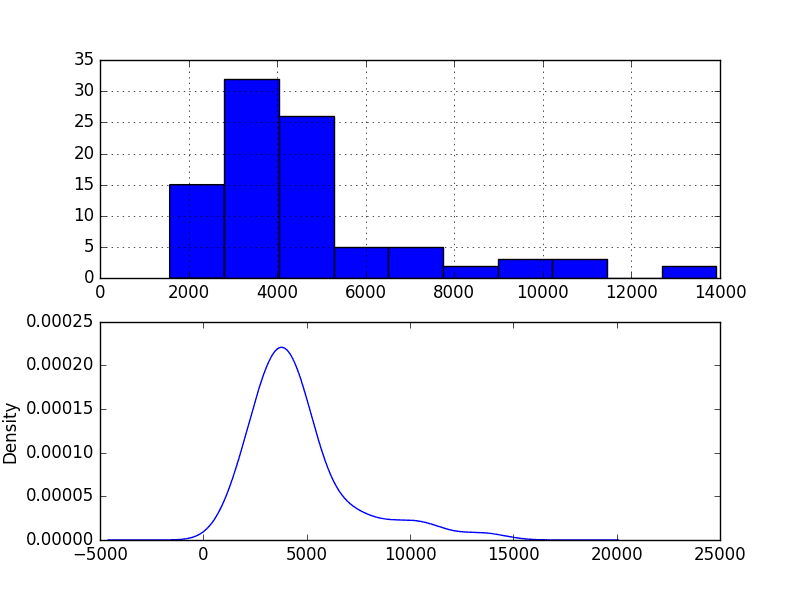
这进一步支持在建模之前探索数据的某些幂变换。

5.5 箱线图

我们可以按年份对月度数据进行分组，并了解每年观测值的分布情况以及它可能如何变化。

我们预计会看到一些趋势（均值或中位数增加），但查看分布的其余部分如何变化可能会很有趣。

下面的示例按年份对观测值进行分组，并为每年的观测值创建一个箱线图。最后一年（1971 年）只包含 9 个月，可能与其他年份的 12 个月观测值不具有可比性。因此，只绘制了 1964 年至 1970 年之间的数据。

运行示例会创建 7 个并排的箱线图，每个图对应所选数据的 7 年中的一年。

回顾这些图可以得出一些观察结果：

• 每年中位数（红线）可能呈增长趋势。
• 数据的分布或中间 50%（蓝色方框）似乎相当稳定。
• 每年都有异常值（黑色十字）；这些可能是季节性周期的顶部或底部。
• 去年，1970 年，看起来与前几年的趋势不同

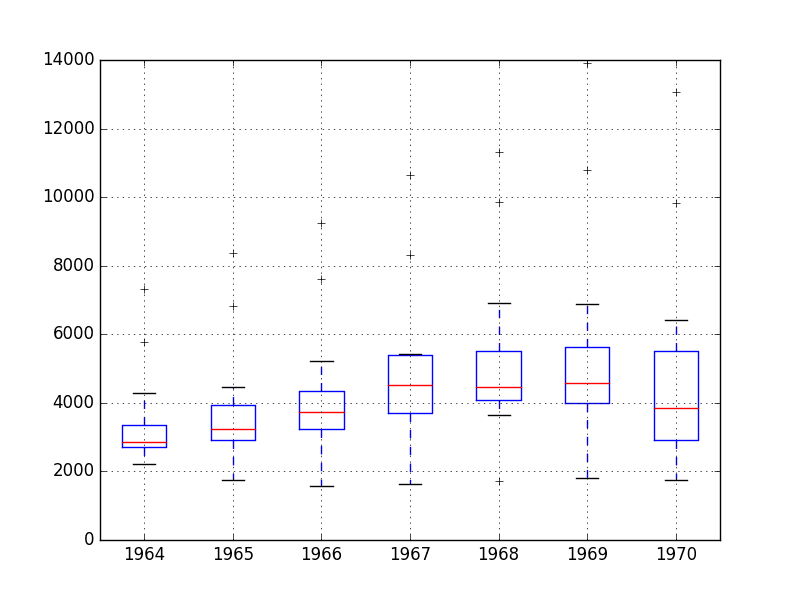
香槟销量箱线图

观测结果表明，可能存在多年的增长趋势和可能是季节性周期一部分的异常值。

这种数据的年度视图是一个有趣的途径，可以通过查看逐年汇总统计数据和逐年汇总统计数据的变化来进一步研究。

6. ARIMA模型

在本节中，我们将为该问题开发自回归综合移动平均 (ARIMA) 模型。

我们将通过手动和自动配置 ARIMA 模型来建模。之后，将是检查所选模型残差错误的第三步。

因此，本节分为 3 个步骤：

1. 手动配置 ARIMA。
2. 自动配置 ARIMA。
3. 审查残差错误。

6.1 手动配置ARIMA

ARIMA(p,d,q) 模型需要三个参数，传统上是手动配置的。

时间序列数据的分析假设我们处理的是平稳时间序列。

时间序列几乎肯定是非平稳的。我们可以通过首先对序列进行差分并使用统计检验来确认结果是平稳的，从而使其平稳。

序列中的季节性似乎是逐年的。季节性数据可以通过从上一周期的同一时间（在本例中为上一年同一月份）的观测值中减去该观测值来差分。这意味着我们将失去第一年的观测值，因为没有上一年可供差分。

下面的示例创建了一个去季节化的序列版本，并将其保存到文件 stationary.csv。

运行示例会输出对差分序列是否平稳的统计显著性检验结果。具体来说，是增广迪基-富勒检验。

结果显示检验统计量值 -7.134898 小于 1% 的临界值 -3.515。这表明我们可以在低于 1% 的显著性水平下拒绝原假设（即结果是统计侥幸的概率很低）。

拒绝零假设意味着该过程没有单位根，进而意味着时间序列是平稳的或不具有时间相关结构。

作为参考，可以通过加上上一年同一月份的观测值来反转季节性差分操作。这在模型对季节性差分数据进行拟合后需要进行预测的情况下是必需的。为了完整性，反转季节性差分操作的函数如下所示。

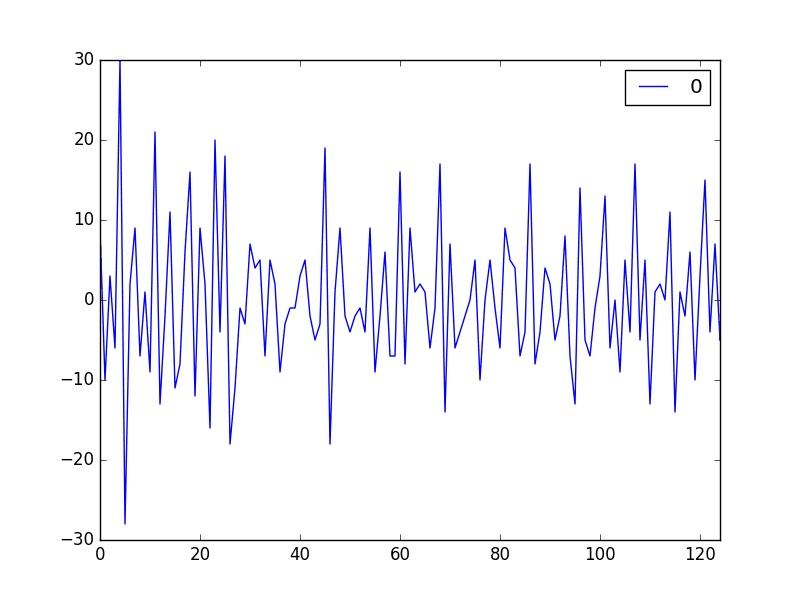
还创建了差分数据集的图。

该图没有显示任何明显的季节性或趋势，表明季节性差分数据集是建模的良好起点。

我们将使用此数据集作为 ARIMA 模型的输入。它还表明可能不需要进一步的差分，并且 d 参数可以设置为 0。

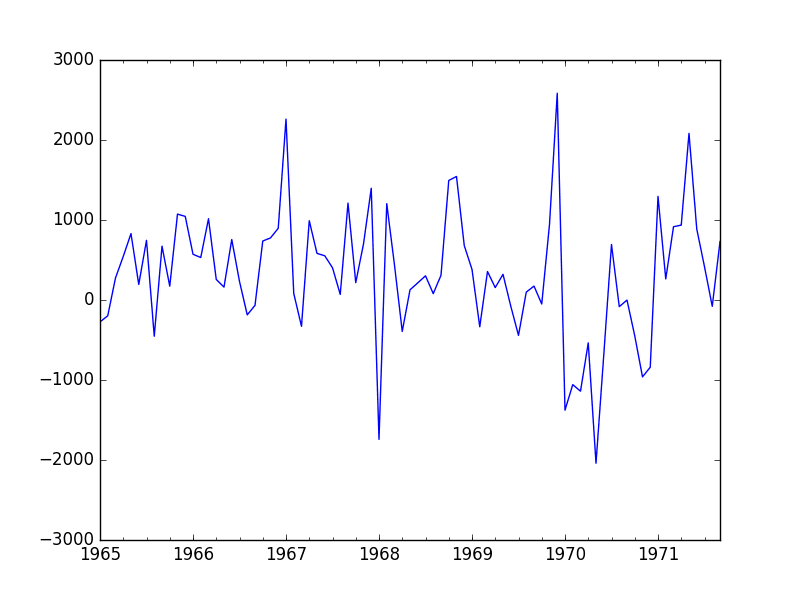
季节性差分香槟销量线图

下一步是选择自回归 (AR) 和移动平均 (MA) 参数 p 和 q 的滞后值。

我们可以通过查看自相关函数（ACF）和偏自相关函数（PACF）图来做到这一点。

请注意，我们现在使用季节性差分的 stationary.csv 作为我们的数据集。

下面的示例为序列生成了 ACF 和 PACF 图。

运行示例并查看图表，以了解如何为 ARIMA 模型设置 p 和 q 变量。

以下是图表中的一些观察结果。

• ACF 显示 1 个月有显著滞后。
• PACF 显示 1 个月有显著滞后，可能在 12 和 13 个月处也有一些显著滞后。
• ACF 和 PACF 都显示在同一点下降，可能表明 AR 和 MA 的混合。

p 和 q 值的一个良好起点也是 1。

PACF 图也表明差分数据中仍然存在一些季节性。

我们可能会考虑一种更好的季节性建模方法，例如直接建模并明确将其从模型中删除，而不是季节性差分。

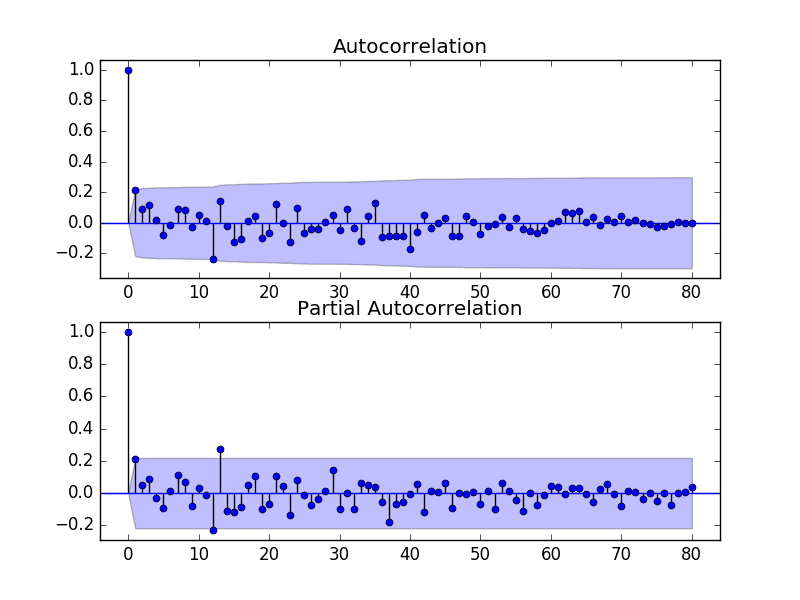
季节性差分香槟销量的 ACF 和 PACF 图

这种快速分析表明，在平稳数据上使用 ARIMA(1,0,1) 或类似模型可能是一个好的起点。

在拟合每个 ARIMA 模型之前，历史观测值将进行季节性差分。所有预测的差分都将反转，以使它们直接与原始销售计数单位中的预期观测值进行比较。

实验表明，这种 ARIMA 配置无法收敛，并导致底层库出现错误。进一步的实验表明，对平稳数据增加一个差分级别使模型更加稳定。模型可以扩展到 ARIMA(1,1,1)。

我们还将通过在调用 fit() 时将“trend”参数设置为“nc”（无常数）来禁用模型中趋势常数的自动添加。根据经验，我发现这可以在某些问题上带来更好的预测性能。

下面的示例演示了此 ARIMA 模型在测试工具上的性能。

请注意，您可能会看到来自底层线性代数库的警告消息；目前可以忽略。

运行此示例会得到 956.942 的 RMSE，这比持久性 RMSE 3186.501 显著提高。

这是一个很好的开始，但我们可能可以通过配置更好的 ARIMA 模型获得更好的结果。

6.2 网格搜索 ARIMA 超参数

ACF 和 PACF 图表明 ARIMA(1,0,1) 或类似模型可能是我们能做到的最好模型。

为了确认此分析，我们可以网格搜索一套ARIMA超参数，并检查没有模型能产生更好的样本外RMSE性能。

在本节中，我们将搜索p、d和q的值以进行组合（跳过那些未能收敛的），并找到在测试集上产生最佳性能的组合。我们将使用网格搜索来探索整数值子集中的所有组合。

具体来说，我们将搜索以下参数的所有组合

• p：0到6。
• d：0到2。
• q：0到6。

这相当于（7 * 3 * 7），即147次潜在的测试运行，执行将需要一些时间。

评估滞后12或13的MA模型可能会很有趣，因为从审查ACF和PACF图来看，这些模型可能具有潜在的趣味性。实验表明，这些模型可能不稳定，导致底层数学库出现错误。

带有网格搜索版本测试框架的完整示例代码如下所示。

运行示例会遍历所有组合，并报告那些没有错误收敛的组合的结果。该示例在现代硬件上运行需要两分钟多一点。

结果显示，发现的最佳配置是ARIMA(0, 0, 1)，RMSE为939.464，略低于上一节中手动配置的ARIMA。这种差异可能具有统计显著性，也可能不具有。

我们将继续选择此ARIMA(0, 0, 1)模型。

6.3 检查残差误差

对模型进行良好最终检查是检查残差预测误差。

理想情况下，残差误差的分布应为零均值的正态分布。

我们可以通过使用汇总统计数据和图表来调查ARIMA(0, 0, 1)模型的残差误差来检查这一点。下面的示例计算并汇总了残差预测误差。

运行示例首先描述残差的分布。

我们可以看到，分布有向右的偏移，并且平均值非零，为165.904728。

这可能表明预测存在偏差。

还绘制了残差误差的分布图。

图表显示了高斯样分布，左尾凹凸不平，进一步证明了幂变换可能值得探索。

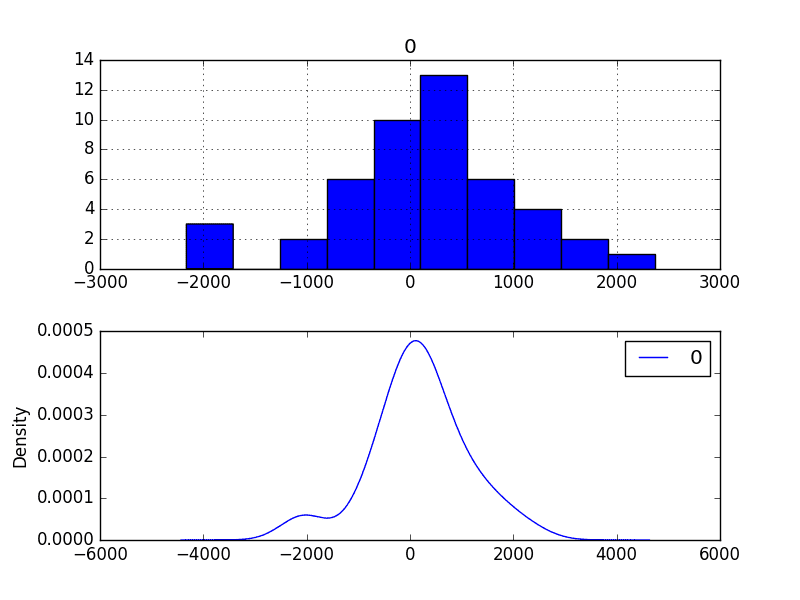
残差预测误差密度图

我们可以利用这些信息，通过在每个预测中加上平均残差误差165.904728来校正预测的偏差。

下面的示例执行了这种偏差关联。

预测的性能从939.464略微提高到924.699，这可能具有统计显著性，也可能不具有。

预测残差误差的摘要显示，平均值确实非常接近零。

最后，残差误差的密度图确实显示出向零的小幅偏移。

这种偏差校正是否值得商榷，但我们暂时会使用它。

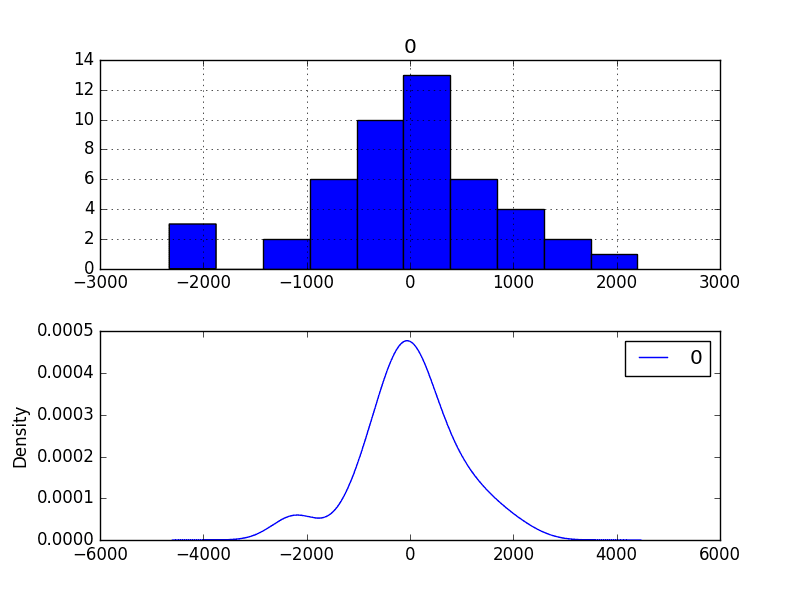
偏差校正后的残差预测误差密度图

检查残差误差的时间序列是否存在任何类型的自相关也是一个好主意。如果存在，则表明模型有更多机会对数据中的时间结构进行建模。

下面的示例重新计算残差误差，并创建ACF和PACF图以检查是否存在任何显著的自相关。

结果表明，时间序列中存在的少量自相关已被模型捕获。

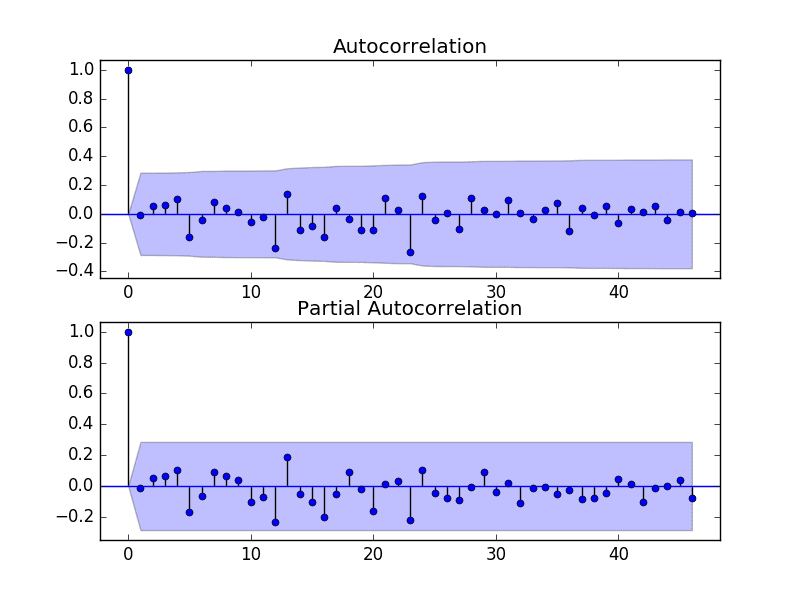
残差预测误差ACF和PACF图

7. 模型验证

在模型开发和选定最终模型后，必须对其进行验证和定稿。

验证是该过程的可选部分，但它提供了一个“最后检查”，以确保我们没有欺骗或误导自己。

本节包括以下步骤：

1. 最终确定模型：训练并保存最终模型。
2. 进行预测：加载已定型的模型并进行预测。
3. 验证模型：加载并验证最终模型。

7.1 最终确定模型

模型的最终确定涉及在整个数据集上拟合ARIMA模型，在本例中是在整个数据集的转换版本上。

一旦拟合，模型可以保存到文件中以供以后使用。

下面的示例在数据集上训练ARIMA(0,0,1)模型，并将整个拟合对象和偏差保存到文件中。

下面的示例将拟合模型以正确的状态保存到文件中，以便以后可以成功加载。

运行示例将创建两个本地文件：

• model.pkl 这是从调用ARIMA.fit()返回的ARIMAResult对象。它包括系数和拟合模型时返回的所有其他内部数据。
• model_bias.npy 这是作为一行一列NumPy数组存储的偏差值。

7.2 进行预测

一个自然的需求可能是加载模型并进行单次预测。

这相对简单，涉及恢复保存的模型和偏差并调用forecast()方法。为了反转季节性差分，还必须加载历史数据。

下面的示例加载模型，预测下一个时间步，并打印预测。

运行示例会打印出大约6794的预测值。

如果我们查看validation.csv，我们可以看到下一时间段第一行的值为6981。

这个预测值大概是正确的。

7.3 验证模型

我们可以加载模型并以模拟的实际操作方式来使用它。

在测试套件部分，我们将原始数据集的最后12个月保存在一个单独的文件中，以验证最终模型。

我们现在可以加载这个validation.csv文件，并用它来查看我们的模型在“未见”数据上的表现如何。

我们有两种可能的方法：

• 加载模型并使用它预测未来12个月。超出前一两个月的预测技能会迅速下降。
• 加载模型并以滚动预测的方式使用它，为每个时间步更新转换和模型。这是首选方法，因为它是在实践中使用此模型的方式，因为它将实现最佳性能。

与前面章节中的模型评估一样，我们将以滚动预测的方式进行预测。这意味着我们将遍历验证数据集中的提前期，并将观测值作为历史的更新。

运行示例将打印出验证数据集中时间步长的每个预测值和期望值。

验证期的最终RMSE预测为3.6111亿销售额。

这比每月超过9.24亿销售额的误差预期要好得多。

同时还提供了预测与验证数据集的比较图。

在此图的尺度上，12个月的预测销售数据看起来非常棒。

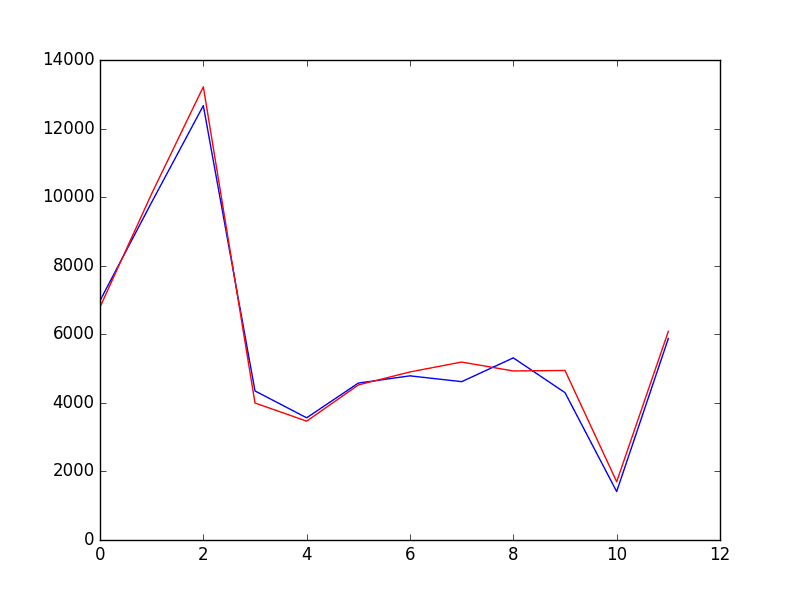
香槟销量验证数据集预测

总结

在本教程中，您发现了使用 Python 进行时间序列预测项目的步骤和工具。

本教程涵盖了大量内容；具体而言

• 如何开发具有性能度量和评估方法的测试框架，以及如何快速开发基线预测和技能。
• 如何使用时间序列分析来提出关于如何最佳地对预测问题进行建模的想法。
• 如何开发 ARIMA 模型、保存它，然后稍后加载它以对新数据进行预测。

您做得怎么样？您对本教程有任何疑问吗？
在下面的评论中提出你的问题，我会尽力回答。

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

...只需几行python代码

在我的新电子书中探索如何实现
Python 时间序列预测入门

它涵盖了**自学教程**和**端到端项目**，主题包括：*数据加载、可视化、建模、算法调优*等等。

最终将时间序列预测带入
您自己的项目

跳过学术理论。只看结果。

查看内容