线性回归是一种简单而强大的技术,用于根据其他变量预测变量的值。它通常用于建模两个或多个连续变量之间的关系,例如收入与年龄之间的关系,或体重与身高之间的关系。同样,线性回归可以用于预测连续结果,例如价格或数量需求,基于已知会影响这些结果的其他变量。
为了训练线性回归模型,我们需要定义一个成本函数和一个优化器。成本函数用于衡量我们的模型与数据的拟合程度,而优化器决定了朝哪个方向移动以改进这种拟合。
在之前的教程中,您学习了如何仅使用线性回归前向传播进行简单预测,而在这里,您将使用 PyTorch 训练线性回归模型并更新其学习参数。具体来说,您将学习:
- 如何在 PyTorch 中从头构建一个简单的线性回归模型。
- 如何将一个简单的线性回归模型应用于数据集。
- 如何在一个可学习参数上训练一个简单的线性回归模型。
- 如何在两个可学习参数上训练一个简单的线性回归模型。
通过我的《用PyTorch进行深度学习》一书来启动你的项目。它提供了包含可用代码的自学教程。
那么,让我们开始吧。

在 PyTorch 中训练线性回归模型。
图片来源:Ryan Tasto。保留部分权利。
概述
本教程分为四个部分;它们是:
- 准备数据
- 构建模型和损失函数
- 训练单个参数的模型
- 训练两个参数的模型
准备数据
让我们导入本教程中将使用的一些库,并为我们的实验创建一些数据。
|
1 2 3 |
import torch import numpy as np import matplotlib.pyplot as plt |
我们将使用合成数据来训练线性回归模型。我们将初始化一个变量 X,其值为 $-5$ 到 $5$,并创建一个斜率为 $-5$ 的线性函数。请注意,这个函数将在以后由我们训练的模型进行估计。
|
1 2 3 4 |
... # 创建一个斜率为 -5 的函数 f(X) X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X |
此外,我们将使用 matplotlib 在线图中查看数据。
|
1 2 3 4 5 6 7 8 |
... # 用红色网格绘制线 plt.plot(X.numpy(), func.numpy(), 'r', label='func') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid('True', color='y') plt.show() |
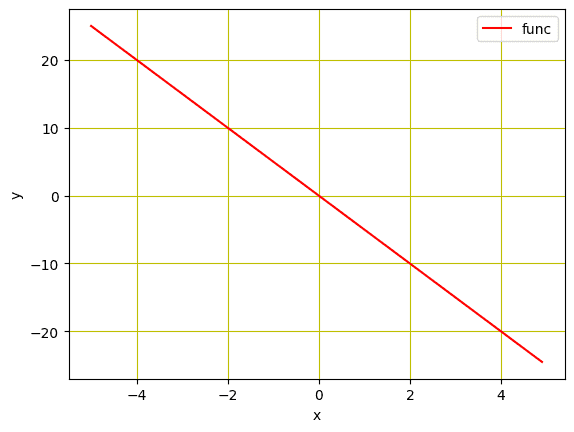
线性函数图
为了模拟我们刚刚创建的真实数据,让我们添加一些高斯噪声来创建与 $X$ 大小相同的噪声数据,并将标准差的值保持在 0.4。这将通过使用 torch.randn(X.size()) 来完成。
|
1 2 3 |
... # 将高斯噪声添加到函数 f(X) 并将其保存在 Y 中 Y = func + 0.4 * torch.randn(X.size()) |
现在,让我们使用下面的代码行可视化这些数据点。
|
1 2 3 4 5 6 7 8 |
# 绘制并可视化蓝色数据点 plt.plot(X.numpy(), Y.numpy(), 'b+', label='Y') plt.plot(X.numpy(), func.numpy(), 'r', label='func') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid('True', color='y') plt.show() |
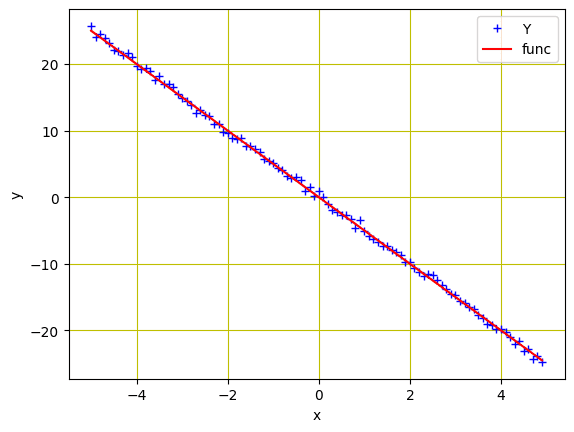
数据点和线性函数
综合来看,以下是完整的代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import torch import numpy as np import matplotlib.pyplot as plt # 创建一个斜率为 -5 的函数 f(X) X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X # 将高斯噪声添加到函数 f(X) 并将其保存在 Y 中 Y = func + 0.4 * torch.randn(X.size()) # 绘制并可视化蓝色数据点 plt.plot(X.numpy(), Y.numpy(), 'b+', label='Y') plt.plot(X.numpy(), func.numpy(), 'r', label='func') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid('True', color='y') plt.show() |
构建模型和损失函数
我们创建了用于输入模型的数据,接下来我们将基于一个简单的线性回归方程构建一个前向函数。请注意,我们这里将构建模型以仅训练一个参数 ($w$)。稍后,在本教程的下一部分中,我们将添加偏差并训练模型以用于两个参数 ($w$ 和 $b$)。模型的前向传播函数定义如下:
|
1 2 3 |
# 定义用于预测的前向传播函数 def forward(x): return w * x |
在训练步骤中,我们需要一个标准来衡量原始数据点和预测数据点之间的损失。这些信息对于模型的梯度下降优化操作至关重要,并且在每次迭代后都会更新,以计算梯度并最小化损失。通常,线性回归用于连续数据,其中均方误差(MSE)有效地计算模型损失。因此,MSE 指标是我们此处使用的标准函数。
|
1 2 3 |
# 使用均方误差评估数据点。 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) |
想开始使用PyTorch进行深度学习吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
训练单个参数的模型
准备就绪后,我们就可以进行模型训练了。首先,参数 $w$ 需要随机初始化,例如,初始化为 $-10$。
|
1 |
w = torch.tensor(-10.0, requires_grad=True) |
接下来,我们将定义学习率或步长,一个空列表用于存储每次迭代后的损失,以及我们希望模型训练的迭代次数。步长设置为 0.1,我们每 epoch 训练模型 20 次迭代。
|
1 2 3 |
step_size = 0.1 loss_list = [] iter = 20 |
当执行以下代码行时,forward() 函数接受输入并生成预测。criterian() 函数计算损失并将其存储在 loss 变量中。根据模型损失,backward() 方法计算梯度,并且 w.data 存储更新后的参数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
for i in range (iter): # 使用前向传播进行预测 Y_pred = forward(X) # 计算原始数据点和预测数据点之间的损失 loss = criterion(Y_pred, Y) # 将计算出的损失存储在列表中 loss_list.append(loss.item()) # 反向传播计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data # 每次迭代后清零梯度 w.grad.data.zero_() # 打印值以便理解 print('{},\t{},\t{}'.format(i, loss.item(), w.item())) |
模型训练的输出如下所示。如您所见,模型损失在每次迭代后都会减少,并且可训练参数(在本例中为 $w$)会更新。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
0, 207.40255737304688, -1.6875505447387695 1, 92.3563003540039, -7.231954097747803 2, 41.173553466796875, -3.5338361263275146 3, 18.402894973754883, -6.000481128692627 4, 8.272472381591797, -4.355228900909424 5, 3.7655599117279053, -5.452612400054932 6, 1.7604843378067017, -4.7206573486328125 7, 0.8684477210044861, -5.208871364593506 8, 0.471589595079422, -4.883232593536377 9, 0.2950323224067688, -5.100433826446533 10, 0.21648380160331726, -4.955560684204102 11, 0.1815381944179535, -5.052190780639648 12, 0.16599132120609283, -4.987738609313965 13, 0.15907476842403412, -5.030728340148926 14, 0.15599775314331055, -5.002054214477539 15, 0.15462875366210938, -5.021179676055908 16, 0.15401971340179443, -5.008423328399658 17, 0.15374873578548431, -5.016931533813477 18, 0.15362821519374847, -5.011256694793701 19, 0.15357455611228943, -5.015041828155518 |
我们还可以通过绘图来可视化损失如何减少。
|
1 2 3 4 5 6 7 |
# 绘制每次迭代后的损失 plt.plot(loss_list, 'r') plt.tight_layout() plt.grid('True', color='y') plt.xlabel("Epochs/Iterations") plt.ylabel("Loss") plt.show() |
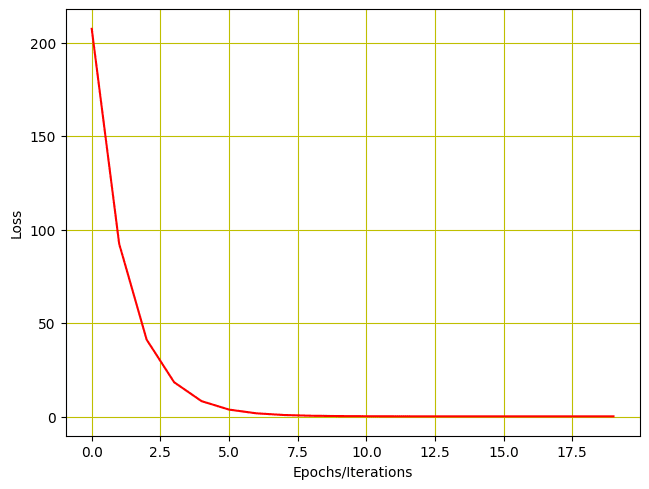
训练损失 vs. 迭代次数
把所有东西放在一起,下面是完整的代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
import torch import numpy as np import matplotlib.pyplot as plt X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X Y = func + 0.4 * torch.randn(X.size()) # 定义用于预测的前向传播函数 def forward(x): return w * x # 使用均方误差评估数据点 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) w = torch.tensor(-10.0, requires_grad=True) step_size = 0.1 loss_list = [] iter = 20 for i in range (iter): # 使用前向传播进行预测 Y_pred = forward(X) # 计算原始数据点和预测数据点之间的损失 loss = criterion(Y_pred, Y) # 将计算出的损失存储在列表中 loss_list.append(loss.item()) # 反向传播计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data # 每次迭代后清零梯度 w.grad.data.zero_() # 打印值以便理解 print('{},\t{},\t{}'.format(i, loss.item(), w.item())) # 绘制每次迭代后的损失 plt.plot(loss_list, 'r') plt.tight_layout() plt.grid('True', color='y') plt.xlabel("Epochs/Iterations") plt.ylabel("Loss") plt.show() |
训练两个参数的模型
我们还在模型中添加偏差 $b$,并训练它以获得两个参数。首先,我们需要将前向函数更改为如下所示。
|
1 2 3 |
# 定义用于预测的前向传播函数 def forward(x): return w * x + b |
由于我们有两个参数 $w$ 和 $b$,我们需要将两者都初始化为一些随机值,如下所示。
|
1 2 |
w = torch.tensor(-10.0, requires_grad = True) b = torch.tensor(-20.0, requires_grad = True) |
虽然所有其他训练代码将保持不变,但我们只需对两个可学习参数进行一些更改。
保持学习率为 0.1,让我们训练我们的模型,使用两个参数进行 20 次迭代/epochs。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
step_size = 0.1 loss_list = [] iter = 20 for i in range (iter): # 使用前向传播进行预测 Y_pred = forward(X) # 计算原始数据点和预测数据点之间的损失 loss = criterion(Y_pred, Y) # 将计算出的损失存储在列表中 loss_list.append(loss.item()) # 反向传播计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后清零梯度 w.grad.data.zero_() b.grad.data.zero_() # 打印值以便理解 print('{}, \t{}, \t{}, \t{}'.format(i, loss.item(), w.item(), b.item())) |
这是我们得到的输出。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
0, 598.0744018554688, -1.8875503540039062, -16.046640396118164 1, 344.6290283203125, -7.2590203285217285, -12.802828788757324 2, 203.6309051513672, -3.6438119411468506, -10.261493682861328 3, 122.82559204101562, -6.029742240905762, -8.19227409362793 4, 75.30597686767578, -4.4176344871521, -6.560757637023926 5, 46.759193420410156, -5.476595401763916, -5.2394232749938965 6, 29.318675994873047, -4.757054805755615, -4.19294548034668 7, 18.525297164916992, -5.2265238761901855, -3.3485677242279053 8, 11.781207084655762, -4.90494441986084, -2.677760124206543 9, 7.537606239318848, -5.112729549407959, -2.1378984451293945 10, 4.853880405426025, -4.968738555908203, -1.7080869674682617 11, 3.1505300998687744, -5.060482025146484, -1.3627978563308716 12, 2.0666630268096924, -4.99583625793457, -1.0874838829040527 13, 1.3757448196411133, -5.0362019538879395, -0.8665863275527954 14, 0.9347621202468872, -5.007069110870361, -0.6902718544006348 15, 0.6530535817146301, -5.024737358093262, -0.5489290356636047 16, 0.4729837477207184, -5.011539459228516, -0.43603143095970154 17, 0.3578317165374756, -5.0192131996154785, -0.34558138251304626 18, 0.28417202830314636, -5.013190746307373, -0.27329811453819275 19, 0.23704445362091064, -5.01648473739624, -0.2154112160205841 |
同样,我们可以绘制损失历史。
|
1 2 3 4 5 6 7 |
# 绘制每次迭代后的损失 plt.plot(loss_list, 'r') plt.tight_layout() plt.grid('True', color='y') plt.xlabel("Epochs/Iterations") plt.ylabel("Loss") plt.show() |
损失图如下所示。
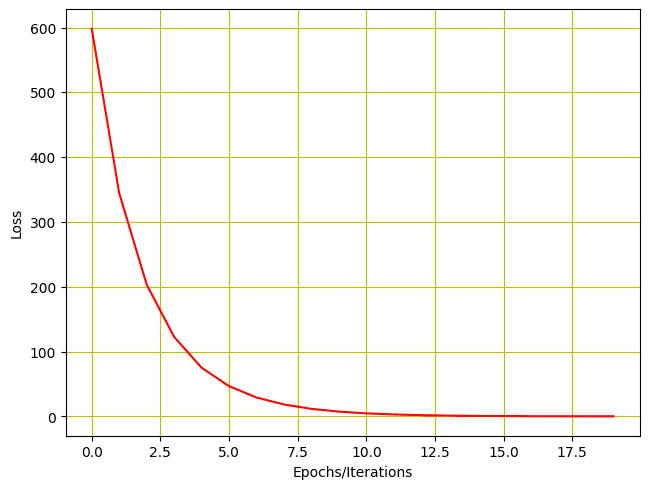
使用两个参数进行训练的损失历史
把所有东西放在一起,这就是完整的代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
import torch import numpy as np import matplotlib.pyplot as plt X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X Y = func + 0.4 * torch.randn(X.size()) # 定义用于预测的前向传播函数 def forward(x): return w * x + b # 使用均方误差评估数据点。 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) step_size = 0.1 loss_list = [] iter = 20 for i in range (iter): # 使用前向传播进行预测 Y_pred = forward(X) # 计算原始数据点和预测数据点之间的损失 loss = criterion(Y_pred, Y) # 将计算出的损失存储在列表中 loss_list.append(loss.item()) # 反向传播计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后清零梯度 w.grad.data.zero_() b.grad.data.zero_() # 打印值以便理解 print('{}, \t{}, \t{}, \t{}'.format(i, loss.item(), w.item(), b.item())) # 绘制每次迭代后的损失 plt.plot(loss_list, 'r') plt.tight_layout() plt.grid('True', color='y') plt.xlabel("Epochs/Iterations") plt.ylabel("Loss") plt.show() |
总结
在本教程中,您学习了如何在 PyTorch 中构建和训练一个简单的线性回归模型。具体来说,您学习了。
- 如何在 PyTorch 中从头构建一个简单的线性回归模型。
- 如何将一个简单的线性回归模型应用于数据集。
- 如何在一个可学习参数上训练一个简单的线性回归模型。
- 如何在两个可学习参数上训练一个简单的线性回归模型。







我喜欢看到这样的例子。我们常常直接使用最大最复杂的模型。线性回归对于许多问题来说都非常强大。更不用说线性回归是可解释的,而深度神经网络则不是。我认为对于大多数问题,我们可以先应用回归方法并评估学习和预测。
感谢您的反馈和支持,Stephen!我们非常感谢!