在我们的 PyTorch 系列上一节中，我们展示了当使用均方误差 (MSE) 损失时，初始化不当的权重如何影响分类模型的准确性。我们注意到模型在训练过程中没有收敛，并且其准确性也显著降低。
接下来，您将看到如果随机初始化权重并使用交叉熵作为模型训练的损失函数会发生什么。这种损失函数更适合逻辑回归和其他分类问题。因此，交叉熵损失被用于当今大多数分类问题。
在本教程中，您将使用交叉熵损失训练一个逻辑回归模型，并对测试数据进行预测。具体来说，您将学习
- 如何在 PyTorch 中使用交叉熵损失训练逻辑回归模型。
- 交叉熵损失如何影响模型准确性。
通过我的《用PyTorch进行深度学习》一书来启动你的项目。它提供了包含可用代码的自学教程。
让我们开始吧。
在 PyTorch 中使用交叉熵损失训练逻辑回归。
图片来源：Y K。保留部分权利。
概述
本教程分为三个部分；它们是
- 准备数据和构建模型
- 使用交叉熵进行模型训练
- 使用测试数据进行验证
准备数据和模型
就像之前的教程一样，您将构建一个类来获取数据集以执行实验。该数据集将分为训练样本和测试样本。测试样本是用于衡量训练模型性能的未见数据。
首先，我们创建一个 Dataset 类
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import torch 从 torch.utils.data 导入 Dataset # 创建数据集类 class Data(Dataset): # 构造函数 def __init__(self): self.x = torch.arange(-2, 2, 0.1).view(-1, 1) self.y = torch.zeros(self.x.shape[0], 1) self.y[self.x[:, 0] > 0.2] = 1 self.len = self.x.shape[0] # Getter def __getitem__(self, idx): return self.x[idx], self.y[idx] # 获取数据长度 def __len__(self): return self.len |
然后，实例化数据集对象。
|
1 2 |
# 创建数据集对象 data_set = Data() |
接下来，您将为我们的逻辑回归模型构建一个自定义模块。它将基于 PyTorch 的 nn.Module 的属性和方法。这个包允许我们为我们的深度学习模型构建复杂的自定义模块，并使整个过程变得容易得多。
该模块只包含一个线性层，如下所示：
|
1 2 3 4 5 6 7 8 9 10 |
# 为逻辑回归构建自定义模块 class LogisticRegression(torch.nn.Module): # 构建构造函数 def __init__(self, n_inputs): super().__init__() self.linear = torch.nn.Linear(n_inputs, 1) # 进行预测 def forward(self, x): y_pred = torch.sigmoid(self.linear(x)) return y_pred |
让我们创建模型对象。
|
1 |
log_regr = LogisticRegression(1) |
该模型应该具有随机权重。您可以通过打印其状态来检查这一点
|
1 |
print("检查参数： ", log_regr.state_dict()) |
您可能会看到
|
1 |
检查参数： OrderedDict([('linear.weight', tensor([[-0.0075]])), ('linear.bias', tensor([0.5364]))]) |
想开始使用PyTorch进行深度学习吗？
立即参加我的免费电子邮件速成课程（附示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
使用交叉熵进行模型训练
回想一下，在之前的教程中，当您将这些参数值与 MSE 损失一起使用时，该模型没有收敛。让我们看看使用交叉熵损失时会发生什么。
由于您正在执行具有一个输出的逻辑回归，因此这是一个具有两个类别的分类问题。换句话说，这是一个二元分类问题，因此我们使用二元交叉熵。您按如下方式设置优化器和损失函数。
|
1 2 3 4 |
... optimizer = torch.optim.SGD(log_regr.parameters(), lr=2) # 二元交叉熵 criterion = torch.nn.BCELoss() |
接下来，我们准备一个 DataLoader 并训练模型 50 个 epoch。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 将数据加载到数据加载器中 train_loader = DataLoader(dataset=data_set, batch_size=2) # 训练模型 Loss = [] epochs = 50 for epoch in range(epochs): for x,y in train_loader: y_pred = log_regr(x) loss = criterion(y_pred, y) Loss.append(loss.item()) optimizer.zero_grad() loss.backward() optimizer.step() print(f"epoch = {epoch}, loss = {loss}") print("完成！") |
训练期间的输出将如下所示：
|
1 |
检查权重： OrderedDict([('linear.weight', tensor([[-5.]])), ('linear.bias', tensor([-10.]))]) |
如您所见，损失在训练过程中减少并收敛到最小值。我们还将绘制训练图。
|
1 2 3 4 5 6 |
import matplotlib.pyplot as plt plt.plot(Loss) plt.xlabel("迭代次数") plt.ylabel("总损失") plt.show() |
您将看到以下内容：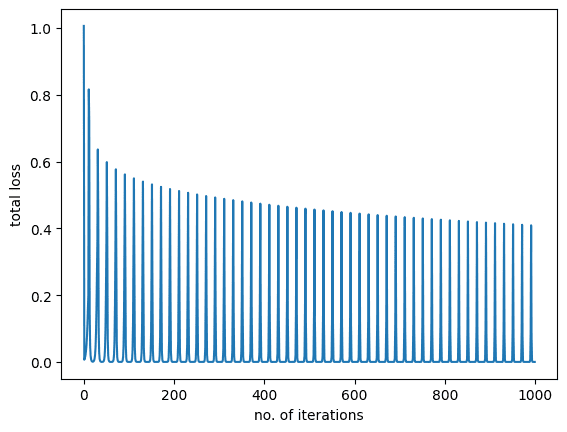
使用测试数据进行验证
上图显示模型在训练数据上表现良好。最后，让我们检查模型在未见数据上的表现。
|
1 2 3 4 5 |
# 获取模型在测试数据上的预测 y_pred = log_regr(data_set.x) label = y_pred > 0.5 # 设置零和一之间的阈值。 print("模型在测试数据上的准确性： ", torch.mean((label == data_set.y.type(torch.ByteTensor)).type(torch.float))) |
结果如下：
|
1 |
模型 在 测试 数据 上的准确性: tensor(1.) |
当模型使用 MSE 损失进行训练时，表现不佳。之前它的准确率约为 57%。但在这里，我们得到了完美的预测。部分原因在于模型简单，是一个单变量逻辑函数。部分原因在于我们正确设置了训练。因此，如我们的实验所示，交叉熵损失显著提高了模型的准确性，优于 MSE 损失。
把所有东西放在一起，下面是完整的代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
导入 matplotlib.pyplot 为 plt import torch 从 torch.utils.data 导入 Dataset, DataLoader torch.manual_seed(0) # 创建数据集类 class Data(Dataset): def __init__(self): self.x = torch.arange(-2, 2, 0.1).view(-1, 1) self.y = torch.zeros(self.x.shape[0], 1) self.y[self.x[:, 0] > 0.2] = 1 self.len = self.x.shape[0] def __getitem__(self, idx): return self.x[idx], self.y[idx] def __len__(self): return self.len # 构建数据集对象 data_set = Data() # 为逻辑回归构建自定义模块 class LogisticRegression(torch.nn.Module): # 构建构造函数 def __init__(self, n_inputs): super().__init__() self.linear = torch.nn.Linear(n_inputs, 1) # 进行预测 def forward(self, x): y_pred = torch.sigmoid(self.linear(x)) return y_pred log_regr = LogisticRegression(1) print("检查参数： ", log_regr.state_dict()) optimizer = torch.optim.SGD(log_regr.parameters(), lr=2) # 二元交叉熵 criterion = torch.nn.BCELoss() # 将数据加载到数据加载器中 train_loader = DataLoader(dataset=data_set, batch_size=2) # 训练模型 Loss = [] epochs = 50 for epoch in range(epochs): for x,y in train_loader: y_pred = log_regr(x) loss = criterion(y_pred, y) Loss.append(loss.item()) optimizer.zero_grad() loss.backward() optimizer.step() print(f"epoch = {epoch}, loss = {loss}") print("完成！") plt.plot(Loss) plt.xlabel("迭代次数") plt.ylabel("总损失") plt.show() # 获取模型在测试数据上的预测 y_pred = log_regr(data_set.x) label = y_pred > 0.5 # 设置零和一之间的阈值。 print("模型在测试数据上的准确性： ", torch.mean((label == data_set.y.type(torch.ByteTensor)).type(torch.float))) |
总结
在本教程中，您学习了交叉熵损失如何影响分类模型的性能。具体来说，您学习了
- 如何在 PyTorch 中使用交叉熵损失训练逻辑回归模型。
- 交叉熵损失如何影响模型准确性。
开始使用PyTorch进行深度学习！
学习如何构建深度学习模型
...使用新发布的PyTorch 2.0库
在我的新电子书中探索如何实现
使用 PyTorch进行深度学习
它提供了包含数百个可用代码的自学教程，让你从新手变成专家。它将使你掌握：
张量操作、训练、评估、超参数优化等等...
嗨，M
代码不错，但我认为您需要对数据进行训练/测试拆分，以证明模型确实泛化良好。