正确进行训练-验证-测试拆分和交叉验证

作者 Adrian Tam 于 2021年9月23日发表在机器学习流程 20

机器学习中的一个关键步骤是模型选择。具有合适超参数的合适模型是获得良好预测结果的关键。当我们面临模型选择时，应该如何做出决定？

这就是为什么我们有交叉验证。在scikit-learn中，有一系列函数可以帮助我们做到这一点。但我们经常看到交叉验证被不当使用，或者交叉验证的结果被错误地解释。

在本教程中，您将发现使用交叉验证来选择项目最佳模型的正确流程和一个数据集。

完成本教程后，您将了解：

数据训练-验证-测试拆分的意义以及不同拆分比例的权衡
评估模型的指标以及如何比较模型
如何使用交叉验证来评估模型
如果我们基于交叉验证做出决策，我们应该怎么做？

让我们开始吧。

正确进行训练-验证-测试拆分和交叉验证。
照片来源：Conal Gallagher，部分权利保留。

教程概述

本教程分为三个部分

模型选择的问题
样本外评估
使用交叉验证进行模型选择工作流程的示例

模型选择的问题

机器学习的成果是一个能够进行预测的模型。最常见的案例是分类模型和回归模型；前者用于预测输入的类别成员身份，后者用于根据输入预测因变量的值。然而，在这两种情况下，我们都有多种模型可供选择。例如，分类模型包括决策树、支持向量机和神经网络等。其中任何一个都依赖于一些超参数。因此，我们必须在开始训练模型之前决定一系列设置。

如果我们根据直觉有两个候选模型，并且想选择一个用于我们的项目，我们应该如何选择？

有一些我们可以普遍使用的标准指标。在回归问题中，我们通常使用以下之一：

均方误差 (MSE)
均方根误差 (RMSE)
平均绝对误差 (MAE)

对于分类问题，常用的指标包括：

准确度
对数损失
F1分数

scikit-learn的指标页面提供了一个更长但并非详尽的常见评估列表，这些评估被分为不同的类别。如果我们有一个样本数据集并想训练一个模型来预测它，我们可以使用这些指标之一来评估模型的效率。

然而，有一个问题；对于样本数据集，我们只评估了一次模型。假设我们正确地将数据集分割为训练集和测试集，并使用训练集拟合模型，同时使用测试集进行评估，我们只获得了与一个测试集相关的单一评估样本点。我们如何确定这是一个准确的评估，而不是偶然过低或过高的值？如果我们有两个模型，并发现一个模型比另一个模型好，我们怎么知道这也不是偶然的？

我们之所以对此感到担忧，是为了避免在模型部署并在未来用于完全不同于我们获取的数据时，出现意外的低准确率。

样本外评估

解决这个问题的方法是训练-验证-测试拆分。

模型最初在训练数据集上拟合[...]。随后，拟合模型用于预测第二个数据集（称为验证数据集）中观测值的响应[...]。最后，测试数据集是用于对在训练数据集上拟合的最终模型进行无偏评估的数据集。如果测试数据集中的数据从未在训练中使用过（例如在交叉验证中），则测试数据集也称为保留数据集。

— “训练、验证和测试集”，维基百科

之所以这样做，在于防止数据泄露的概念。

“衡量什么就会改进什么”，或者如古德哈特定律所说，“当一个度量成为目标时，它就不再是一个好的度量了。”如果我们使用一组数据来选择模型，那么我们选择的模型在同一组数据下，使用相同的评估指标，肯定会表现良好。然而，我们应该关心的是未见过的数据上的评估指标。

因此，我们需要在整个模型选择和训练过程中保留一部分数据，并将其用于最终评估。这部分数据是我们模型的“期末考试”，模型必须在此之前不能看到考题。确切地说，数据的使用流程如下：

训练数据集用于训练几个候选模型
验证数据集用于评估候选模型
选择一个候选模型
选择的模型使用新的训练数据集进行训练
训练好的模型使用测试数据集进行评估

在步骤 1 和 2 中，我们不想只评估候选模型一次。相反，我们希望使用不同的数据集多次评估每个模型，并在步骤 3 中根据平均分数做出决定。如果我们拥有大量数据，这很容易做到。否则，我们可以使用k折交叉验证技巧来多次重新采样同一数据集，并假装它们是不同的。当我们评估模型或超参数时，模型必须从头开始训练，每次都要避免重用前几次尝试的训练结果。我们称此过程为交叉验证。

根据交叉验证的结果，我们可以判断一个模型是否优于另一个模型。由于交叉验证是在较小的数据集上进行的，当我们决定了模型后，我们可能想再次重新训练模型。原因与我们在交叉验证中使用k折的原因相同；我们没有很多数据，而我们之前使用的小数据集有一部分被保留用于验证。我们认为结合训练集和验证集可以产生更好的模型。这就是步骤 4 中发生的情况。

步骤 5 中的评估数据集，与我们在交叉验证中使用的不同，因为我们不希望数据泄露。如果它们是相同的，我们将看到与交叉验证中已看到的相同的分数。或者更糟的是，由于测试集是我们用来训练所选模型的数据的一部分，并且我们已经为该测试数据集调整了模型，因此测试分数将保证是好的。

完成训练后，我们想要（1）将此模型与我们之前的评估进行比较，以及（2）估计它在部署后的表现。

我们使用从未在先前步骤中使用过的测试数据集来评估性能。因为这是未见过的数据，它可以帮助我们评估泛化能力或样本外误差。这应该模拟模型部署后的情况。如果存在过拟合，我们预计在此评估中的误差会很高。

同样，如果我们正确地进行了模型训练，我们预计此评估分数与我们在上一步交叉验证中获得的分数不会有太大差异。这可以作为我们模型选择的确认。

使用交叉验证进行模型选择工作流程的示例

在下文中，我们将虚构一个回归问题来阐述模型选择工作流程应该如何进行。

首先，我们使用numpy生成一个数据集

...
# Generate data and plot
N = 300
x = np.linspace(0, 7*np.pi, N)
smooth = 1 + 0.5*np.sin(x)
y = smooth + 0.2*np.random.randn(N)

...

# 生成数据并绘图

N = 300

x = np.linspace(0, 7*np.pi, N)

smooth = 1 + 0.5*np.sin(x)

y = smooth + 0.2*np.random.randn(N)

我们生成一个正弦曲线并添加一些噪声。本质上，数据是：

$$y=1 + 0.5\sin(x) + \epsilon$$

其中 $\epsilon$ 是一个小的噪声信号。数据如下所示：

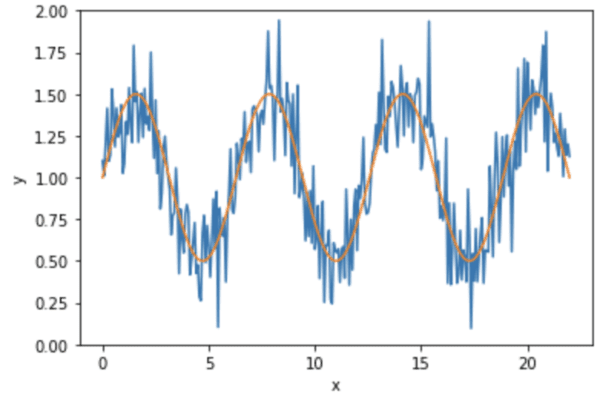
然后我们进行训练-测试拆分，并在完成最终模型之前保留测试集。由于我们将使用scikit-learn模型进行回归，并且它们假定输入 `x` 是二维数组，所以我们在这里先进行重塑。此外，为了更明显地体现模型选择的效果，我们在拆分时没有打乱数据。实际上，这通常不是一个好主意。

...
# Train-test split, intentionally use shuffle=False
X = x.reshape(-1,1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, shuffle=False)

...

# 训练-测试拆分，特意使用 shuffle=False

X = x.reshape(-1,1)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, shuffle=False)

下一步，我们创建两个回归模型。它们分别是二次

$$y = c + b\times x + a\times x^2$$

和线性

$$y = b + a\times x$$

scikit-learn中没有多项式回归，但我们可以使用`PolynomialFeatures`结合`LinearRegression`来实现。`PolynomialFeatures(2)`会将输入 $x$ 转换为 $1, x, x^2$，并在这些上的线性回归将找到我们上面公式中的系数 $a, b, c$。

...
# Create two models: Quadratic and linear regression
polyreg = make_pipeline(PolynomialFeatures(2), LinearRegression(fit_intercept=False))
linreg = LinearRegression()

...

# 创建两个模型：二次和线性回归

polyreg = make_pipeline(PolynomialFeatures(2), LinearRegression(fit_intercept=False))

linreg = LinearRegression()

下一步是仅使用训练集并对两个模型中的每一个应用k折交叉验证

...
# Cross-validation
scoring = "neg_root_mean_squared_error"
polyscores = cross_validate(polyreg, X_train, y_train, scoring=scoring, return_estimator=True)
linscores = cross_validate(linreg, X_train, y_train, scoring=scoring, return_estimator=True)

...

# 交叉验证

scoring = "neg_root_mean_squared_error"

polyscores = cross_validate(polyreg, X_train, y_train, scoring=scoring, return_estimator=True)

linscores = cross_validate(linreg, X_train, y_train, scoring=scoring, return_estimator=True)

函数 `cross_validate()` 返回一个 Python 字典，如下所示：

{'fit_time': array([0.00177097, 0.00117302, 0.00219226, 0.0015142 , 0.00126314]),
 'score_time': array([0.00054097, 0.0004108 , 0.00086379, 0.00092077, 0.00043106]),
 'estimator': [Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),
                               ('linearregression', LinearRegression(fit_intercept=False))]),
               Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),
                               ('linearregression', LinearRegression(fit_intercept=False))]),
               Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),
                               ('linearregression', LinearRegression(fit_intercept=False))]),
               Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),
                               ('linearregression', LinearRegression(fit_intercept=False))]),
               Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),
                               ('linearregression', LinearRegression(fit_intercept=False))])],
 'test_score': array([-1.00421665, -0.53397399, -0.47742336, -0.41834582, -0.68043053])}

{'fit_time': array([0.00177097, 0.00117302, 0.00219226, 0.0015142 , 0.00126314]),

'score_time': array([0.00054097, 0.0004108 , 0.00086379, 0.00092077, 0.00043106]),

'estimator': [Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),

('linearregression', LinearRegression(fit_intercept=False))]),

Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),

('linearregression', LinearRegression(fit_intercept=False))]),

Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),

('linearregression', LinearRegression(fit_intercept=False))]),

Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),

('linearregression', LinearRegression(fit_intercept=False))]),

Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),

('linearregression', LinearRegression(fit_intercept=False))])],

'test_score': array([-1.00421665, -0.53397399, -0.47742336, -0.41834582, -0.68043053])}

其中 `test_score` 键保存了每个折叠的分数。我们使用负均方根误差进行交叉验证，分数越高，误差越小，模型就越好。

以上是二次模型的。线性模型的相应测试分数如下：

array([-0.43401194, -0.52385836, -0.42231028, -0.41532203, -0.43441137])

1	array([-0.43401194, -0.52385836, -0.42231028, -0.41532203, -0.43441137])

通过比较平均分数，我们发现线性模型的性能优于二次模型。

...
# Which one is better? Linear and polynomial
print(linscores["test_score"].mean())
print(polyscores["test_score"].mean())
print(linscores["test_score"].mean() - polyscores["test_score"].mean())

...

# 哪个更好？线性与多项式

print(linscores["test_score"].mean())

print(polyscores["test_score"].mean())

print(linscores["test_score"].mean() - polyscores["test_score"].mean())

Linear regression score: -0.4459827970437929
Polynomial regression score: -0.6228780695994603
Difference: 0.17689527255566745

线性回归分数：-0.4459827970437929

多项式回归分数：-0.6228780695994603

差值：0.17689527255566745

在继续训练我们选择的模型之前，我们可以说明一下发生了什么。以第一次交叉验证迭代为例，我们可以看到二次回归的系数如下：

...
# Let's show the coefficient of the first fitted polynomial regression
# This starts from the constant term and in ascending order of powers
print(polyscores["estimator"][0].steps[1][1].coef_)

...

# 让我们展示第一个拟合的多项式回归的系数

# 这从常数项开始，按幂次升序排列

print(polyscores["estimator"][0].steps[1][1].coef_)

[-0.03190358 0.20818594 -0.00937904]

1	[-0.03190358 0.20818594 -0.00937904]

这意味着我们拟合的二次模型是：

$$y=-0.0319 + 0.2082\times x – 0.0094\times x^2$$

而其交叉验证第一次迭代中的线性回归系数是：

...
# And show the coefficient of the last-fitted linear regression
print(linscores["estimator"][0].intercept_, linscores["estimator"][-1].coef_)

...

# 并显示最后一次拟合的线性回归的系数

print(linscores["estimator"][0].intercept_, linscores["estimator"][-1].coef_)

0.856999187854241 [-0.00918622]

1	0.856999187854241 [-0.00918622]

这意味着拟合的线性模型是：

$$y = 0.8570 – 0.0092\times x$$

我们可以在图表中看到它们的样子：

...
# Plot and compare
plt.plot(x, y)
plt.plot(x, smooth)
plt.plot(x, polyscores["estimator"][0].predict(X))
plt.plot(x, linscores["estimator"][0].predict(X))
plt.ylim(0,2)
plt.xlabel("x")
plt.ylabel("y")
plt.show()

...

# 绘图和比较

plt.plot(x, y)

plt.plot(x, smooth)

plt.plot(x, polyscores["estimator"][0].predict(X))

plt.plot(x, linscores["estimator"][0].predict(X))

plt.ylim(0,2)

plt.xlabel("x")

plt.ylabel("y")

plt.show()

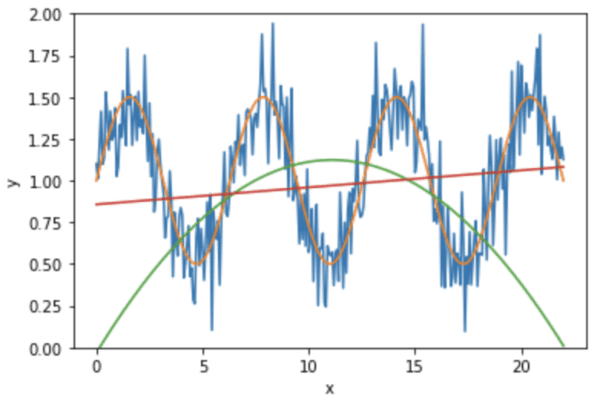
在这里，我们看到红线是线性回归，而绿线来自二次回归。我们可以看到二次曲线在两端都与输入数据（蓝曲线）有很大偏差。

由于我们决定使用线性模型进行回归，我们需要重新训练模型并使用我们保留的测试数据进行测试。

...
# Retrain the model and evaluate
linreg.fit(X_train, y_train)
print("Test set RMSE:", mean_squared_error(y_test, linreg.predict(X_test), squared=False))
print("Mean validation RMSE:", -linscores["test_score"].mean())

...

# 重新训练模型并评估

linreg.fit(X_train, y_train)

print("Test set RMSE:", mean_squared_error(y_test, linreg.predict(X_test), squared=False))

print("Mean validation RMSE:", -linscores["test_score"].mean())

Test set RMSE: 0.4403109417232645
Mean validation RMSE: 0.4459827970437929

1 2	测试集 RMSE：0.4403109417232645 平均验证 RMSE：0.4459827970437929

在这里，由于 scikit-learn 会在每次交叉验证迭代时克隆一个新模型，因此我们创建的模型在交叉验证后仍未训练。否则，我们应该使用 `linreg = sklearn.base.clone(linreg)` 重置模型。但从上面可以看出，我们从测试集中获得的均方根误差为 0.440，而从交叉验证中获得的分数为 0.446。两者差异不大，因此我们可以得出结论，该模型在新的数据上应该会看到类似数量级的误差。

将所有这些结合起来，完整的例子如下所示。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import cross_validate, train_test_split
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

np.random.seed(42)

# Generate data and plot
N = 300
x = np.linspace(0, 7*np.pi, N)
smooth = 1 + 0.5*np.sin(x)
y = smooth + 0.2*np.random.randn(N)
plt.plot(x, y)
plt.plot(x, smooth)
plt.xlabel("x")
plt.ylabel("y")
plt.ylim(0,2)
plt.show()

# Train-test split, intentionally use shuffle=False
X = x.reshape(-1,1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, shuffle=False)

# Create two models: Polynomial and linear regression
degree = 2
polyreg = make_pipeline(PolynomialFeatures(degree), LinearRegression(fit_intercept=False))
linreg = LinearRegression()

# Cross-validation
scoring = "neg_root_mean_squared_error"
polyscores = cross_validate(polyreg, X_train, y_train, scoring=scoring, return_estimator=True)
linscores = cross_validate(linreg, X_train, y_train, scoring=scoring, return_estimator=True)

# Which one is better? Linear and polynomial
print("Linear regression score:", linscores["test_score"].mean())
print("Polynomial regression score:", polyscores["test_score"].mean())
print("Difference:", linscores["test_score"].mean() - polyscores["test_score"].mean())

print("Coefficients of polynomial regression and linear regression:")
# Let's show the coefficient of the last fitted polynomial regression
# This starts from the constant term and in ascending order of powers
print(polyscores["estimator"][0].steps[1][1].coef_)
# And show the coefficient of the last-fitted linear regression
print(linscores["estimator"][0].intercept_, linscores["estimator"][-1].coef_)

# Plot and compare
plt.plot(x, y)
plt.plot(x, smooth)
plt.plot(x, polyscores["estimator"][0].predict(X))
plt.plot(x, linscores["estimator"][0].predict(X))
plt.ylim(0,2)
plt.xlabel("x")
plt.ylabel("y")
plt.show()

# Retrain the model and evaluate
import sklearn
linreg = sklearn.base.clone(linreg)
linreg.fit(X_train, y_train)
print("Test set RMSE:", mean_squared_error(y_test, linreg.predict(X_test), squared=False))
print("Mean validation RMSE:", -linscores["test_score"].mean())

import matplotlib.pyplot as plt

import numpy as np

from sklearn.model_selection import cross_validate, train_test_split

from sklearn.preprocessing import PolynomialFeatures, StandardScaler

from sklearn.pipeline import make_pipeline

from sklearn.linear_model import LinearRegression

from sklearn.metrics import mean_squared_error

np.random.seed(42)

# 生成数据并绘图

N = 300

x = np.linspace(0, 7*np.pi, N)

smooth = 1 + 0.5*np.sin(x)

y = smooth + 0.2*np.random.randn(N)

plt.plot(x, y)

plt.plot(x, smooth)

plt.xlabel("x")

plt.ylabel("y")

plt.ylim(0,2)

plt.show()

# 训练-测试拆分，特意使用 shuffle=False

X = x.reshape(-1,1)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, shuffle=False)

# 创建两个模型：多项式和线性回归

degree = 2

polyreg = make_pipeline(PolynomialFeatures(degree), LinearRegression(fit_intercept=False))

linreg = LinearRegression()

# 交叉验证

scoring = "neg_root_mean_squared_error"

polyscores = cross_validate(polyreg, X_train, y_train, scoring=scoring, return_estimator=True)

linscores = cross_validate(linreg, X_train, y_train, scoring=scoring, return_estimator=True)

# 哪个更好？线性与多项式

print("Linear regression score:", linscores["test_score"].mean())

print("Polynomial regression score:", polyscores["test_score"].mean())

print("Difference:", linscores["test_score"].mean() - polyscores["test_score"].mean())

print("Coefficients of polynomial regression and linear regression:")

# 让我们展示最后一次拟合的多项式回归的系数

# 这从常数项开始，按幂次升序排列

print(polyscores["estimator"][0].steps[1][1].coef_)

# 并显示最后一次拟合的线性回归的系数

print(linscores["estimator"][0].intercept_, linscores["estimator"][-1].coef_)

# 绘图和比较

plt.plot(x, y)

plt.plot(x, smooth)

plt.plot(x, polyscores["estimator"][0].predict(X))

plt.plot(x, linscores["estimator"][0].predict(X))

plt.ylim(0,2)

plt.xlabel("x")

plt.ylabel("y")

plt.show()

# 重新训练模型并评估

import sklearn

linreg = sklearn.base.clone(linreg)

linreg.fit(X_train, y_train)

print("Test set RMSE:", mean_squared_error(y_test, linreg.predict(X_test), squared=False))

print("Mean validation RMSE:", -linscores["test_score"].mean())

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

教程

API

sklearn.model_selection.KFold API。
sklearn.model_selection.cross_val_score API。
sklearn.model_selection.cross_validate API。

文章

交叉验证（统计学），维基百科。

总结

在本教程中，您学习了如何进行数据集的训练-验证-测试拆分，如何进行k折交叉验证来正确选择模型，以及如何在选择后重新训练模型。

具体来说，你学到了：

训练-验证-测试拆分对于模型选择的重要性
如何使用训练集上的k折交叉验证来评估和比较机器学习模型。
如何根据交叉验证的建议选择模型后重新训练模型
如何使用测试集来确认我们的模型选择

关于此主题的更多信息

交叉验证, 训练-测试拆分

粒子群优化入门

如何学习用于机器学习的Python

对“正确进行训练-验证-测试拆分和交叉验证”的20条回复

Jeremy 2021年9月25日 12:50 下午 #

Adrian,

这又是一篇非常棒的文章！如果可以的话，我想就你在这里的内容提出几个问题：

1) 在什么情况下，设置 Shuffle=False 是有益的？
2) 根据您的经验，您认为多大的数据集才足以单独使用保留集而不是交叉验证？

这绝对是我想要掌握的机器学习方面，因为我做这类工作才一年左右。非常感谢您的时间！

回复
- Adrian Tam 2021年9月27日 10:29 上午 #
  
  (1) 您几乎总应该打乱数据。除非是时间序列，因为那样会扭曲时间轴。
  (2) 这取决于您的模型复杂度。出于某种神秘原因，统计学中有个魔数30。所以我的粗略估计是，模型参数数量的30倍就足以进行一次保留。
  
  回复
tia 2021年10月15日 1:42 下午 #

你好！

总结一下：
1. 对整个数据集进行多模型CV
2. 从步骤 1 中选择最佳模型
3. 使用步骤 2 中的模型对训练-测试拆分的数据进行拟合和预测

这样对吗？如果是的话，我有时会看到一个例子，其中CV在训练数据上进行，然后最佳模型用于在测试数据上进行预测。这也对吗？

一如既往，非常感谢您，Adrian Tam先生！

回复
- Adrian Tam 2021年10月20日 7:54 上午 #
  
  在我看来，这两种方式都可以。但使用仅训练数据进行CV是更优选和更实用的。考虑一下，测试数据是我明天才会拿到的。所以我将使用今天的数据进行CV，找到最佳模型。然后构建它。然后明天测试它，并说服人们它很好（因为我构建它时不知道测试数据，但它能很好地预测）。然后我可以在下周将训练好的模型投入生产使用。
  
  回复
  - tia 2021年10月21日 5:51 下午 #
    
    我明白了，非常感谢您，先生！
    
    回复
  - AGGELOS PAPOUTSIS 2022年1月7日 11:12 下午 #
    
    嗨，
    
    当你提到训练数据时，你是说将 X（自变量）输入到 cross-val 中吗？
    
    还是你使用训练-测试拆分，然后将 x_train, y_train 输入到 cross-val 中？
    
    谢谢
    
    回复
David B Rosen 2021年10月16日 5:47 上午 #

嗨 Adrian，好文章！值得一提的是，永远不要在进行训练-测试-验证分割或在过采样数据上进行交叉验证*之前*进行过采样（包括 SMOTE 等）。使用交叉验证进行过采样的正确方法是在交叉验证循环*内部*执行过采样，*仅*对在该特定迭代的交叉验证中使用的训练折进行过采样。否则，您将得到一些重复或依赖的过采样实例同时出现在训练折和验证折中，这使得它们不独立，并部分无效化和偏倚了交叉验证。一种正确的方法是构建一个包含内置过采样功能的管道，使用 imbalanced-learn 包中的 create_pipeline_imb()，然后对该管道执行交叉验证（例如 GridSearchCV）作为您的模型，尽管我还没有尝试过这个特定方法。

回复
- David B Rosen 2021年10月16日上午5:50 #
  
  更正一下，应该是 make_pipeline_imb()，而不是 create_pipeline_imb()。
  
  回复
- Adrian Tam 2021年10月20日上午8:35 #
  
  感谢您的建议。那是正确的。事实上，您所描述的被称为数据泄露，是我们应该在验证中避免的（否则您的验证分数就不准确了）。
  
  回复
haider 2021年10月29日下午5:38 #

如何解释测试准确率远高于训练准确率的事实？

回复
- Adrian Tam 2021年10月30日下午12:36 #
  
  很可能是碰巧。
  
  回复
S 2022年3月14日上午9:00 #

嗨，感谢这篇教程！

在第 3 步（“选择一个候选模型”）之后，您写道：
4. 选择的模型使用新的训练数据集进行训练
5. 训练好的模型使用测试数据集进行评估

问题：在第 4 步和第 5 步之间，是否应该有一个步骤，您使用选定的模型再次执行交叉验证和超参数调整？（因为您处理的是不同的训练集。）

回复
- James Carmichael 2022年3月14日上午11:46 #
  
  嗨 S……这实际上可能会提高训练性能和准确性。
  
  回复
PRIYA K S 2022年4月14日下午7:05 #

先生您好。Sklearn 的 “cross_validate” 和 sklearn 的 “Kfold” 有什么关系？它们是用于执行相同类型 KFold 交叉验证的相似函数，还是两者之间有区别？我问这个问题是因为您的另一篇教程提到了显式配置 KFold 交叉验证。

提前感谢您的澄清。

回复
- James Carmichael 2022年4月15日上午7:24 #
  
  嗨 Priya……以下资源可能有助于澄清。
  
  https://medium.com/gustavorsantos/how-to-do-cross-validation-kfold-and-grid-search-in-python-e570cdb20a28
  
  回复
Priya K S 2022年4月22日下午8:04 #

非常感谢您提供的参考文章！

回复
Priya K S 2022年4月22日下午8:10 #

非常感谢您提供的参考文章。

回复
Yunhao 2022年8月11日上午3:21 #

亲爱的 Jason,

为了清楚起见

步骤 2 验证数据集用于评估候选模型。此处，验证数据集 = y_train

步骤 4 选择的模型使用新的训练数据集进行训练。此处，新的训练数据集 = X_train + y_train

这些对吗？

回复
- James Carmichael 2022年8月11日上午6:10 #
  
  嗨 Yunhao……感谢您的反馈！您的理解是正确的。
  
  回复
  - Jaber 2023年9月7日上午4:51 #
    
    你好，
    谢谢您的教程。
    
    我有 2 个问题，请。
    
    问题 1：我们在第 61 行克隆了 linreg 模型。为什么？
    
    问题 2：为什么我们在第 61 行不直接写
    linreg = LinearRegression()
    就像我们在第 30 行之前做的那样？
    
    谢谢
    
    回复

导航

正确进行训练-验证-测试拆分和交叉验证

教程概述

模型选择的问题

样本外评估

使用交叉验证进行模型选择工作流程的示例

进一步阅读

教程

API

文章

总结

关于此主题的更多信息

对“正确进行训练-验证-测试拆分和交叉验证”的20条回复

Leave a Reply Click here to cancel reply.

导航

教程概述

模型选择的问题

样本外评估

使用交叉验证进行模型选择工作流程的示例

进一步阅读

教程

API

文章

总结

关于此主题的更多信息

对*“正确进行训练-验证-测试拆分和交叉验证”*的20条回复

Leave a Reply Click here to cancel reply.

对“正确进行训练-验证-测试拆分和交叉验证”的20条回复