如何在 Weka 中调整机器学习算法

你可以通过调整机器学习算法的参数（称为超参数）来最大限度地发挥其作用。

在这篇文章中，你将了解如何在Weka中通过受控实验调整机器学习算法。

阅读本文后，您将了解

• 通过算法调优提高机器学习模型性能的重要性。
• 如何设计一个受控实验来调整机器学习算法的超参数。
• 如何使用统计显著性解释调优实验的结果。

通过我的新书《Weka机器学习精通》启动你的项目，其中包含所有示例的分步教程和清晰的屏幕截图。

让我们开始吧。

如何在 Weka 中调整机器学习算法
照片由Andrei Niemimäki拍摄，部分权利保留。

通过调优提高性能

机器学习算法可以配置以表现出不同的行为。

这很有用，因为它允许它们的行为适应你的机器学习问题的具体情况。

这也是一个难题，因为你必须选择如何配置算法，而事先不知道哪种配置最适合你的问题。

因此，你必须针对你的问题调整每个机器学习算法的配置参数。这通常被称为算法调优或算法超参数优化。

这是一个经验性的试错过程。

你可以尝试调整算法，以发现导致你的问题表现最佳的参数组合，但这可能很困难，因为你必须记录所有结果并手动进行比较。

一个更可靠的方法是设计一个受控实验来评估一些预定义的算法配置，并提供工具来审查和比较结果。

Weka实验环境提供了一个接口，允许你设计、执行和分析这些类型的实验的结果。

算法调优实验概述

在本教程中，我们将定义一个实验来研究k近邻（kNN）机器学习算法的参数。

我们将研究kNN算法的两个参数：

1. k值，即查询以进行预测的邻居数量。
2. 距离度量，即在查询中确定邻居以进行预测的方式。

我们将使用Pima Indians糖尿病发病数据集。每个实例代表一名患者的医疗详细信息，任务是预测该患者是否会在未来五年内患上糖尿病。有8个数值输入变量，所有变量的尺度都不同。

• 数据集文件.
• 数据集详情.

最佳结果的准确率约为77%。

本教程分为3个部分：

1. 设计实验
2. 运行实验
3. 审查实验结果

你可以使用这种实验设计作为基础，在自己的数据集上调整不同机器学习算法的参数。

1. 设计实验

在本节中，我们将定义实验。

我们将选择用于评估不同算法配置的数据集。我们还将添加kNN算法（在Weka中称为IBk）的多个实例，每个实例都具有不同的算法配置。

1. 打开Weka GUI选择器

2. 单击“Experimenter”按钮打开Weka Experimenter界面。

Weka实验环境

3. 在“Setup”选项卡上，单击“New”按钮开始新实验。

4. 在“Dataset”窗格中，单击“Add new…”按钮并选择data/diabetes.arff。

5. 在“Algorithms”窗格中，单击“Add new…”按钮，单击“Choose”按钮，并在“lazy”组下选择“IBk”算法。单击“OK”按钮将其添加。

这已添加k=1且距离为欧几里得的kNN。

重复此过程并添加配置参数如下的IBk。k参数可在算法配置中的“KNN”参数中指定。

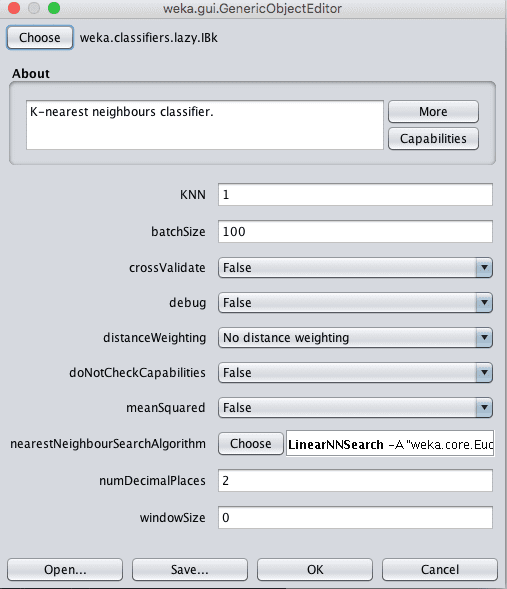
Weka k近邻算法配置

可以通过单击“nearestNeighbourSearchAlgorithm”参数的技术名称来更改距离度量，以打开搜索方法的配置属性，然后单击“distanceFunction”参数的“Choose”按钮。

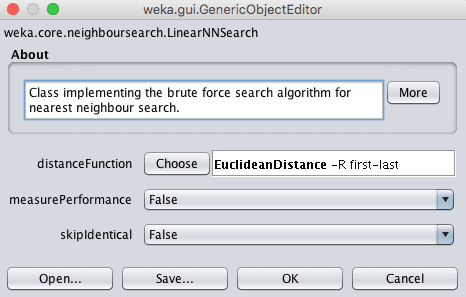
Weka为k近邻算法选择距离函数

请注意，你可以通过单击“Algorithms”窗格中的“Edit selected…”按钮来编辑添加到实验中的算法配置。

• IBk，k=3，distanceFunction=欧几里得
• IBk，k=7，distanceFunction=欧几里得
• IBk，k=1，distanceFunction=曼哈顿
• IBk，k=3，distanceFunction=曼哈顿
• IBk，k=7，distanceFunction=曼哈顿

欧几里得距离是一种距离度量，最适用于数据集中所有输入属性具有相同尺度的情况。曼哈顿距离是一种距离度量，最适用于输入属性具有不同尺度的情况，例如Pima Indians糖尿病发病数据集。

我们期望带有曼哈顿距离度量的kNN将从本实验中获得更好的整体分数。

实验使用10折交叉验证（默认）。每个配置将在数据集上评估10次（10次10折交叉验证），使用不同的随机数种子。这将导致每个评估的算法配置产生10个略有不同的结果，这是一个我们可以稍后使用统计方法解释的小样本。

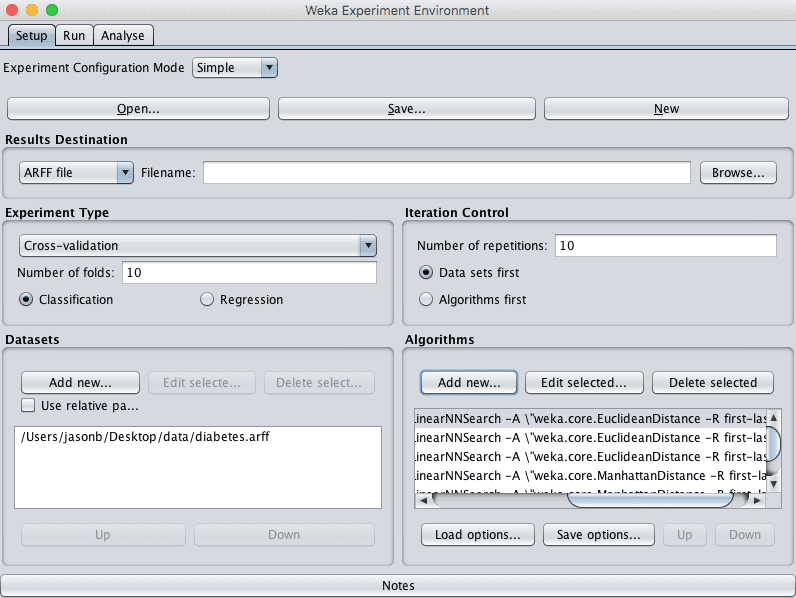
Weka配置算法调优实验

2. 运行实验

现在是时候运行实验了。

1. 单击“Run”选项卡。

这里有几个选项。你只能开始或停止正在运行的实验。

2. 单击“Start”按钮并运行实验。它应该在几秒钟内完成。这是因为数据集很小。

Weka运行算法调优实验

3. 审查实验结果

通过单击“Source”窗格中的“Experiment”按钮加载我们刚刚执行的实验结果。

Weka加载算法调优实验结果

你会看到加载了600个结果。这是因为我们有6种算法配置，每种配置都评估了100次，即10折交叉验证乘以10次重复。

我们将使用配对统计显著性检验，根据正确百分比比较每种算法配置。所有默认配置。

比较的基础是列表中的第一个算法，即k=1且距离度量为欧几里得的IBK，也是添加到实验中的第一个算法，也是默认选择。

单击“Actions”窗格中的“Perform test”按钮。

你将看到一个结果表，如下所示：

结果令人着迷。

我们可以看到，总体而言，欧几里得距离度量比曼哈顿距离度量取得了更好的结果，但基础算法（k=1，欧几里得距离）与所有三种曼哈顿距离配置之间的差异并不显著（结果值旁边没有“*”）。

我们还可以看到，使用k=3或k=7的欧几里得距离确实导致了比基础算法更高的准确率，并且这种差异具有统计显著性（结果旁边有一个小“v”）。

算法(3)（k=7，欧几里得距离）是否显著优于其他结果？

我们可以通过选择此算法作为比较基础轻松进行此比较。

1. 单击“Test base”旁边的“Select”按钮。
2. 单击第三个算法，k=7，距离度量为欧几里得。
3. 单击“Select”按钮将其选为基础。
4. 单击“Perform Test”按钮以生成结果报告。

Weka为结果分析选择新的测试基准

你将看到一个结果表，如下所示。

我们可以看到，与k=1使用欧几里得或曼哈顿距离相比，k=7和欧几里得距离的差异具有统计学意义，但与k=3或7（无论距离度量如何）相比则不具备。

这很有帮助。它告诉我们，我们可能可以同样轻松地使用曼哈顿或欧几里得距离，并使用k=7或k=3，并获得相似的结果。

所选的基础算法的准确率确实最高，为74.45%。这种差异在较低的显著性水平（例如20%）下可能具有统计显著性（通过将“significance”设置为0.20），但方差会非常高（在5个随机实例中，有4个更好），因此结果可能不够可靠。

这些结果除了寻找“最佳”之外，还在其他方面很有用。我们或许可以看到k值增加时准确率的上升趋势。我们可以设计一个后续实验，其中距离度量固定为欧几里得，并考虑更大的k值。

总结

在这篇文章中，你学习了如何设计受控实验来调整机器学习算法的超参数。

具体来说，你学到了

• 关于算法参数的必要性以及根据你的问题经验性地调整它们的重要性。
• 如何在Weka中设计和执行受控实验来调整机器学习算法的参数。
• 如何使用统计显著性解释受控实验的结果。

你对算法调优或这篇文章有什么问题吗？请在评论中提出你的问题，我会尽力回答。

探索无需代码的机器学习！

在几分钟内开发您自己的模型

...只需几次点击

在我的新电子书中探索如何实现
使用 Weka 精通机器学习

涵盖自学教程和端到端项目，例如
加载数据、可视化、构建模型、调优等等...

最终将机器学习应用到你自己的项目中

跳过学术理论。只看结果。

查看内容