深度学习神经网络使用随机梯度下降优化算法进行训练。
学习率是一个超参数,它控制着在模型权重每次更新时,模型根据估计的误差会改变多少。选择学习率是一个挑战,因为太小的值可能导致训练过程漫长且可能陷入停滞,而太大的值可能导致模型过快地学习到次优的权重集,或者导致训练过程不稳定。
在配置神经网络时,学习率可能是最重要的超参数。因此,了解如何研究学习率对模型性能的影响并建立对学习率在模型行为中动态的直观认识至关重要。
在本教程中,您将发现学习率、学习率调度和自适应学习率对模型性能的影响。
完成本教程后,您将了解:
- 高学习率会导致训练不稳定,而极小的学习率会导致训练失败。
- 动量可以加速训练,而学习率调度可以帮助优化过程收敛。
- 自适应学习率可以加速训练,并减轻选择学习率和学习率调度的一些压力。
用我的新书《更好的深度学习》来启动你的项目,书中包含分步教程和所有示例的 Python 源代码文件。
让我们开始吧。
- 更新于 2019 年 2 月:修正了回调函数错误地定义在 compile() 而非 fit() 函数上的问题。
- 2019 年 10 月更新:更新至 Keras 2.3 和 TensorFlow 2.0。
- **2020年1月更新**:已针对 scikit-learn v0.22 API 的变更进行更新。

通过深度学习神经网络理解学习率对模型性能的影响
照片由 Abdul Rahman 拍摄,部分权利保留
教程概述
本教程分为六个部分;它们是:
- 学习率与梯度下降
- 在 Keras 中配置学习率
- 多类别分类问题
- 学习率和动量的影响
- 学习率调度的影响
- 自适应学习率的影响
学习率与梯度下降
深度学习神经网络使用随机梯度下降算法进行训练。
随机梯度下降是一种优化算法,它使用训练数据集中的样本来估计模型当前状态的误差梯度,然后使用误差反向传播算法(简称为反向传播)来更新模型权重。
在训练过程中更新权重的量称为步长或“学习率”。
具体来说,学习率是神经网络训练中一个可配置的超参数,其值通常是一个很小的正数,一般在 0.0 到 1.0 之间。
学习率控制着模型适应问题的速度。较小的学习率需要更多的训练轮次,因为每次更新对权重的改变都很小,而较大的学习率会导致快速改变,需要较少的训练轮次。
过大的学习率可能导致模型过快地收敛到一个次优解,而过小的学习率可能导致过程陷入停滞。
训练深度学习神经网络的挑战在于仔细选择学习率。它可能是模型最重要的超参数。
学习率可能是最重要的超参数。如果你只有时间调整一个超参数,那就调整学习率。
— 第 429 页,《深度学习》,2016 年。
现在我们熟悉了学习率是什么,让我们来看看如何为神经网络配置学习率。
有关学习率是什么以及它是如何工作的,请参阅文章
在 Keras 中配置学习率
Keras 深度学习库允许您轻松地为多种随机梯度下降优化算法变体配置学习率。
随机梯度下降
Keras 提供了 SGD 类,该类实现了具有学习率和动量的随机梯度下降优化器。
首先,必须创建该类的一个实例并进行配置,然后在使用模型上的 fit() 函数时将其指定给“optimizer”参数。
默认学习率为 0.01,默认不使用动量。
|
1 2 3 4 |
from keras.optimizers import SGD ... opt = SGD() model.compile(..., optimizer=opt) |
可以通过“lr”参数指定学习率,通过“momentum”参数指定动量。
|
1 2 3 4 |
from keras.optimizers import SGD ... opt = SGD(lr=0.01, momentum=0.9) model.compile(..., optimizer=opt) |
该类还通过“decay”参数支持学习率衰减。
使用学习率衰减时,学习率的计算方式如下:
|
1 |
lrate = initial_lrate * (1 / (1 + decay * iteration)) |
其中 lrate 是当前轮次的学习率,initial_lrate 是在 SGD 参数中指定的初始学习率,decay 是大于零的衰减率,iteration 是当前的更新次数。
|
1 2 3 4 |
from keras.optimizers import SGD ... opt = SGD(lr=0.01, momentum=0.9, decay=0.01) model.compile(..., optimizer=opt) |
学习率调度
Keras 支持通过回调函数实现学习率调度。
回调函数独立于优化算法运行,但它们会调整优化算法使用的学习率。建议在使用学习率调度回调函数时使用 SGD。
回调函数会被实例化和配置,然后在一个列表中传递给 fit() 函数的“callbacks”参数来训练模型。
Keras 提供了 ReduceLROnPlateau,当检测到模型性能停滞时(例如,在给定的训练轮次数内没有变化),它会调整学习率。此回调函数旨在模型停止改进后降低学习率,以期微调模型权重。
ReduceLROnPlateau 需要您通过“monitor”参数指定训练期间要监控的指标,通过“factor”参数指定学习率将乘以的值,以及“patience”参数,该参数指定在触发学习率变化之前要等待的训练轮次数。
例如,我们可以监控验证损失,如果验证损失在 100 个轮次内没有改善,则将学习率降低一个数量级。
|
1 2 3 4 5 |
# 使用 ReduceLROnPlateau 回调函数的代码片段 from keras.callbacks import ReduceLROnPlateau ... rlrop = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=100) model.fit(..., callbacks=[rlrop]) |
Keras 还提供了 LearningRateScheduler 回调函数,允许您指定一个每轮次调用的函数来调整学习率。
您可以定义一个 Python 函数,该函数接受两个参数(轮次和当前学习率)并返回新的学习率。
|
1 2 3 4 5 6 7 8 9 |
# 使用 LearningRateScheduler 回调函数的代码片段 from keras.callbacks import LearningRateScheduler ... def my_learning_rate(epoch, lrate): return lrate lrs = LearningRateScheduler(my_learning_rate) model.fit(..., callbacks=[lrs]) |
自适应学习率梯度下降
Keras 还提供了一系列简单的随机梯度下降扩展,支持自适应学习率。
由于每种方法都自适应学习率(通常是每个模型权重的学习率),因此通常只需要很少的配置。
三种常用的自适应学习率方法包括:
RMSProp 优化器
|
1 2 3 4 |
from keras.optimizers import RMSprop ... opt = RMSprop() model.compile(..., optimizer=opt) |
Adagrad 优化器
|
1 2 3 4 |
from keras.optimizers import Adagrad ... opt = Adagrad() model.compile(..., optimizer=opt) |
Adam 优化器
|
1 2 3 4 |
from keras.optimizers import Adam ... opt = Adam() model.compile(..., optimizer=opt) |
想要通过深度学习获得更好的结果吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
多类别分类问题
我们将使用一个小型多类别分类问题作为基础,来演示学习率对模型性能的影响。
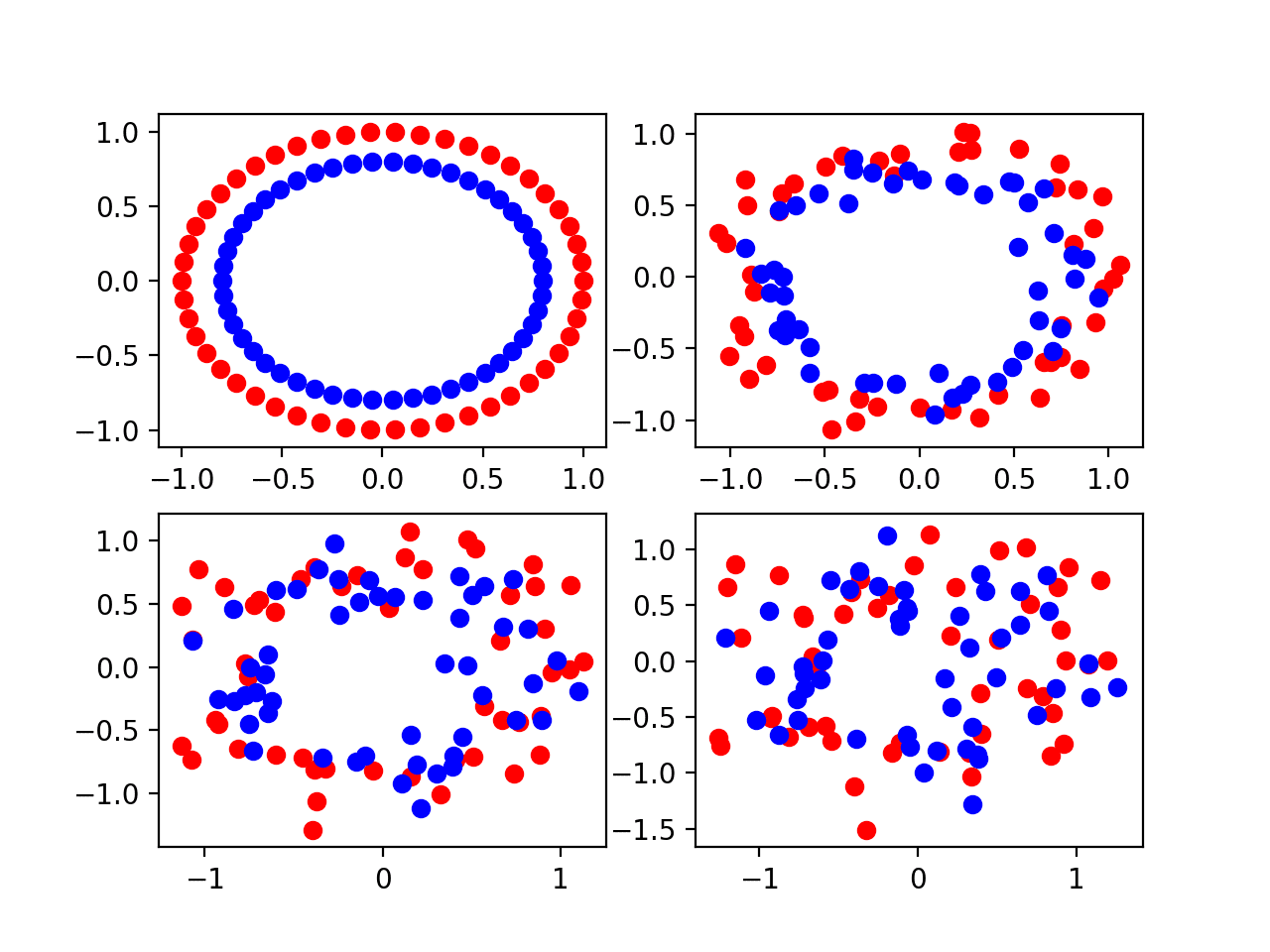
scikit-learn 类提供了 make_blobs() 函数,可用于创建具有指定样本数、输入变量、类别数以及类内样本方差的多类别分类问题。该问题有两个输入变量(表示点的 x 和 y 坐标),每个组内点的标准差为 2.0。我们将使用相同的随机状态(伪随机数生成器的种子),以确保我们始终获得相同的数据点。
该问题有两个输入变量(表示点的 x 和 y 坐标),每个组内点的标准差为 2.0。我们将使用相同的随机状态(伪随机数生成器的种子)以确保我们始终获得相同的数据点。
|
1 2 |
# 生成二维分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) |
结果是我们可以建模的数据集的输入和输出元素。
为了了解问题的复杂性,我们可以在二维散点图上绘制每个点,并根据类别值对每个点进行着色。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# blob 数据集的散点图 from sklearn.datasets import make_blobs from matplotlib import pyplot from numpy import where # 生成二维分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 每个类别值的散点图 for class_value in range(3): # 选择具有类标签的点的索引 row_ix = where(y == class_value) # 绘制不同颜色点的散点图 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 显示图 pyplot.show() |
运行示例将创建整个数据集的散点图。我们可以看到标准差为 2.0 意味着类别并非线性可分(可由一条线分开),导致许多模糊的点。
这是理想的,因为它意味着问题并非微不足道,并且允许神经网络模型找到许多不同“足够好”的候选解决方案。
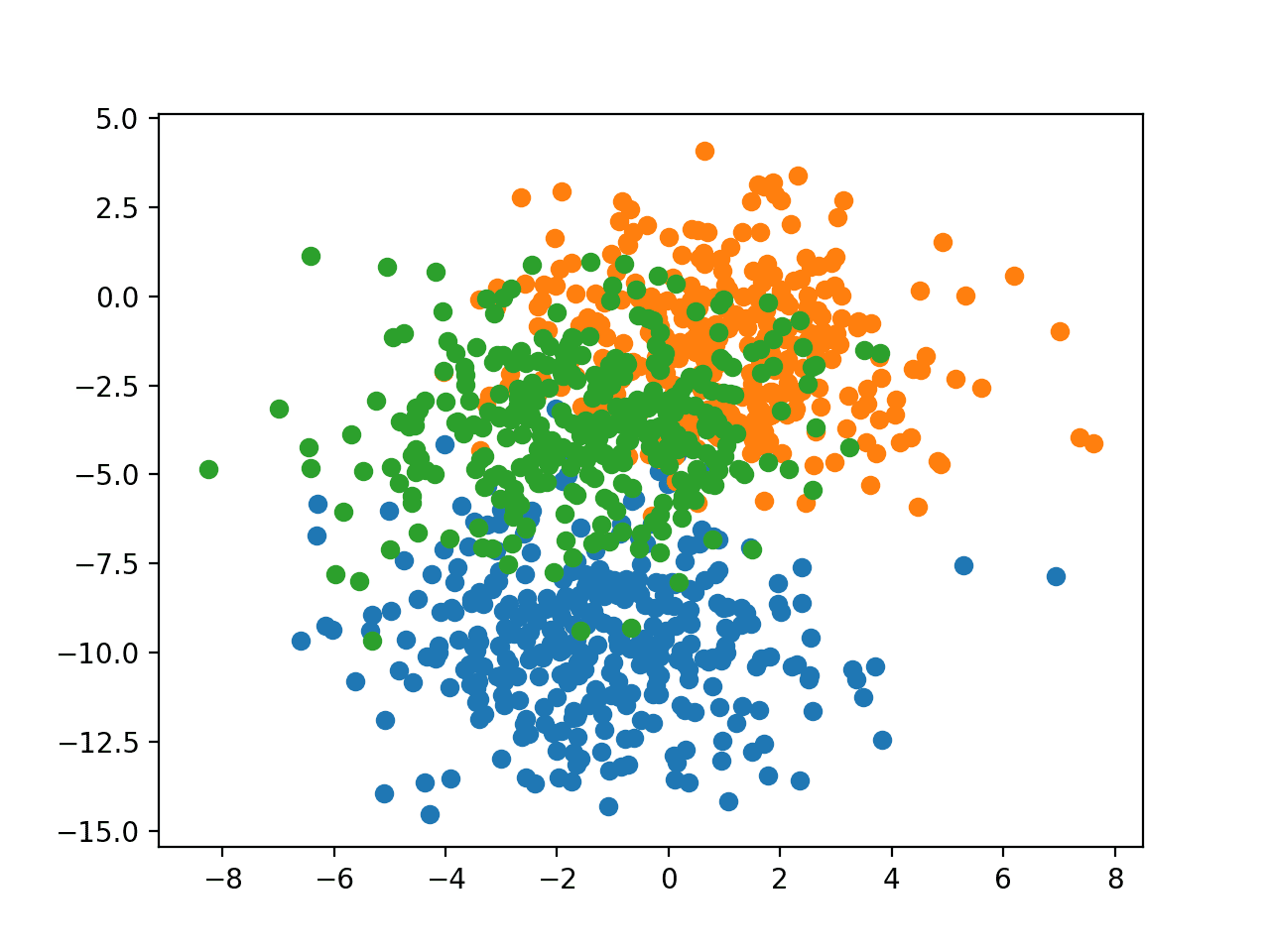
具有三个类别且点按类别值着色的 Blob 数据集散点图
学习率和动量的影响
在本节中,我们将开发一个多层感知机(MLP)模型来解决 this blob 分类问题,并研究不同学习率和动量的影响。
学习率动态
第一步是开发一个函数来创建问题的样本并将其拆分为训练集和测试集。
此外,我们还必须对目标变量进行独热编码,以便我们能够开发一个预测样本属于每个类别的概率的模型。
下面的 `prepare_data()` 函数实现了此行为,将训练集和测试集拆分为输入和输出元素后返回。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 准备训练和测试数据集 def prepare_data(): # 生成 2d 分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 对输出变量进行独热编码 y = to_categorical(y) # 分割为训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] return trainX, trainy, testX, testy |
接下来,我们可以开发一个函数来拟合和评估 MLP 模型。
首先,我们将定义一个简单的 MLP 模型,该模型接受 blobs 问题的两个输入变量,拥有一个包含 50 个节点的隐藏层,以及一个包含三个节点以预测每个类别概率的输出层。隐藏层中的节点将使用整流线性激活函数(ReLU),而输出层中的节点将使用 softmax 激活函数。
|
1 2 3 4 |
# 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) |
我们将使用随机梯度下降优化器,并要求指定学习率,以便我们可以评估不同的速率。模型将通过最小化交叉熵来训练。
|
1 2 3 |
# 编译模型 opt = SGD(lr=lrate) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) |
模型将训练 200 个轮次(通过一些试错法确定),并将测试集用作验证数据集,以便我们了解模型在训练过程中的泛化误差。
|
1 2 |
# 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) |
拟合完成后,我们将绘制模型在训练轮次中在训练集和测试集上的准确率。
|
1 2 3 4 |
# 绘制学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.title('lrate='+str(lrate), pad=-50) |
下面的 `fit_model()` 函数将这些元素结合起来,它将拟合模型并绘制其性能,提供训练和测试数据集以及要评估的特定学习率。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 拟合模型并绘制学习曲线 def fit_model(trainX, trainy, testX, testy, lrate): # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # 编译模型 opt = SGD(lr=lrate) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) # 绘制学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.title('lrate='+str(lrate), pad=-50) |
我们现在可以研究不同学习率对模型训练和测试准确率的动态影响。
在此示例中,我们将以对数刻度评估从 1E-0 (1.0) 到 1E-7 的学习率,并通过调用 `fit_model()` 函数为每个学习率创建折线图。
|
1 2 3 4 5 6 7 8 9 10 |
# 为不同的学习率创建学习曲线 learning_rates = [1E-0, 1E-1, 1E-2, 1E-3, 1E-4, 1E-5, 1E-6, 1E-7] for i in range(len(learning_rates)): # 确定绘图编号 plot_no = 420 + (i+1) pyplot.subplot(plot_no) # 拟合模型并绘制特定学习率的学习曲线 fit_model(trainX, trainy, testX, testy, learning_rates[i]) # 显示学习曲线 pyplot.show() |
将所有这些联系在一起,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# blobs 问题上学习率对准确率的研究 from sklearn.datasets import make_blobs from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from keras.utils import to_categorical from matplotlib import pyplot # 准备训练和测试数据集 def prepare_data(): # 生成 2d 分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 对输出变量进行独热编码 y = to_categorical(y) # 分割为训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] return trainX, trainy, testX, testy # 拟合模型并绘制学习曲线 def fit_model(trainX, trainy, testX, testy, lrate): # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # 编译模型 opt = SGD(lr=lrate) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) # 绘制学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.title('lrate='+str(lrate), pad=-50) # 准备数据集 trainX, trainy, testX, testy = prepare_data() # 为不同的学习率创建学习曲线 learning_rates = [1E-0, 1E-1, 1E-2, 1E-3, 1E-4, 1E-5, 1E-6, 1E-7] for i in range(len(learning_rates)): # 确定绘图编号 plot_no = 420 + (i+1) pyplot.subplot(plot_no) # 拟合模型并绘制特定学习率的学习曲线 fit_model(trainX, trainy, testX, testy, learning_rates[i]) # 显示学习曲线 pyplot.show() |
运行示例将创建一个包含八个不同评估学习率的折线图的单个图形。训练数据集上的分类准确率用蓝色标记,测试数据集上的准确率用橙色标记。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑运行示例几次并比较平均结果。
图表显示,学习率 1.0 出现行为振荡,而学习率 1E-6 和 1E-7 导致模型无法学习任何内容。
我们可以看到,模型在学习率 1E-1、1E-2 和 1E-3 下能够很好地学习问题,尽管随着学习率的降低,学习速度会逐渐变慢。在所选模型配置下,结果表明中等学习率 0.1 在训练集和测试集上都能获得良好的模型性能。
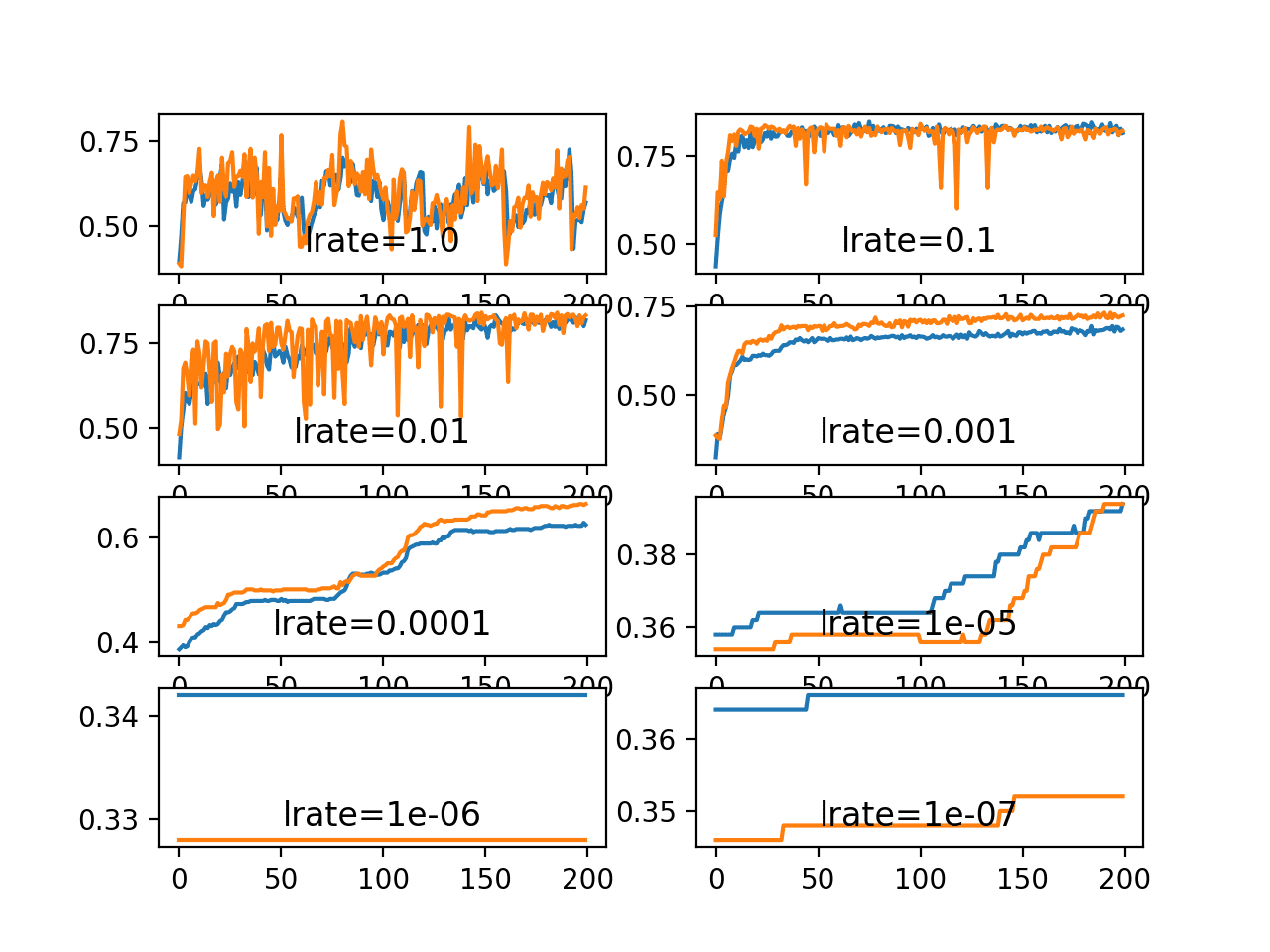
Blobs 分类问题上一系列学习率的训练和测试准确率折线图
动量动态
动量可以平滑学习算法的进程,进而加速训练过程。
我们可以调整前一节的示例,以评估动量在固定学习率下的影响。在这种情况下,我们将选择学习率为 0.01,它在上一节中收敛到了一个合理的结果,但需要的轮次数比学习率 0.1 要多。
可以更新 `fit_model()` 函数以接受“momentum”参数而不是学习率参数,该参数可用于 SGD 类的配置并在结果图中报告。
该函数的更新版本如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 拟合模型并绘制学习曲线 def fit_model(trainX, trainy, testX, testy, momentum): # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # 编译模型 opt = SGD(lr=0.01, momentum=momentum) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) # 绘制学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.title('momentum='+str(momentum), pad=-80) |
通常使用接近 1.0 的动量值,例如 0.9 和 0.99。
在本例中,我们将演示模型在没有动量的情况下与具有 0.5 和更高动量值的模型相比的动态。
|
1 2 3 4 5 6 7 8 9 10 |
# 为不同的动量创建学习曲线 momentums = [0.0, 0.5, 0.9, 0.99] for i in range(len(momentums)): # 确定绘图编号 plot_no = 220 + (i+1) pyplot.subplot(plot_no) # 拟合模型并绘制特定动量的学习曲线 fit_model(trainX, trainy, testX, testy, momentums[i]) # 显示学习曲线 pyplot.show() |
将所有这些联系在一起,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# blobs 问题上动量对准确率的研究 from sklearn.datasets import make_blobs from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from keras.utils import to_categorical from matplotlib import pyplot # 准备训练和测试数据集 def prepare_data(): # 生成 2d 分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 对输出变量进行独热编码 y = to_categorical(y) # 分割为训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] return trainX, trainy, testX, testy # 拟合模型并绘制学习曲线 def fit_model(trainX, trainy, testX, testy, momentum): # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # 编译模型 opt = SGD(lr=0.01, momentum=momentum) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) # 绘制学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.title('momentum='+str(momentum), pad=-80) # 准备数据集 trainX, trainy, testX, testy = prepare_data() # 为不同的动量创建学习曲线 momentums = [0.0, 0.5, 0.9, 0.99] for i in range(len(momentums)): # 确定绘图编号 plot_no = 220 + (i+1) pyplot.subplot(plot_no) # 拟合模型并绘制特定动量的学习曲线 fit_model(trainX, trainy, testX, testy, momentums[i]) # 显示学习曲线 pyplot.show() |
运行示例将创建一个包含四个不同评估动量值的折线图的单个图形。训练数据集上的分类准确率用蓝色标记,测试数据集上的准确率用橙色标记。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑运行示例几次并比较平均结果。
我们可以看到,动量的加入确实加速了模型的训练。具体来说,动量值为 0.9 和 0.99 的模型能在约 50 个训练轮次内达到合理的训练和测试准确率,而未使用动量时则需要 200 个轮次。
在所有使用动量的情况下,模型在留出测试数据集上的准确率似乎更稳定,在训练轮次中表现出较少的波动。
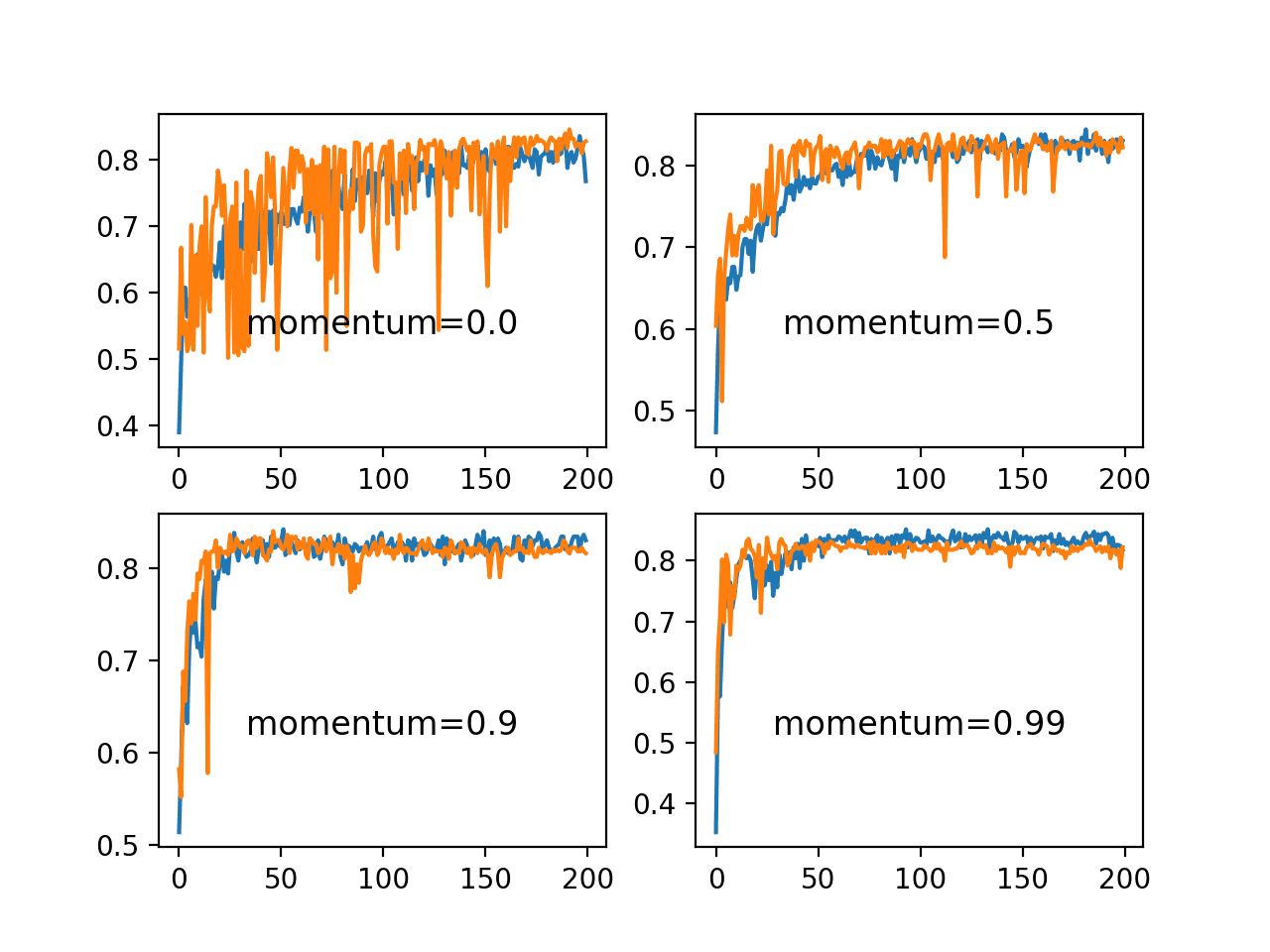
Blobs 分类问题上一系列动量值的训练和测试准确率折线图
学习率调度的影响
在本节中,我们将研究两种学习率调度。
第一个是 SGD 类中内置的衰减,第二个是 `ReduceLROnPlateau` 回调函数。
学习率衰减
`SGD` 类提供了“decay”参数来指定学习率衰减。
从方程或代码中可能不清楚这种衰减对更新期间学习率的影响。我们可以通过一个实际示例使其更清晰。
下面的函数实现了 Keras SGD 类中实现的学习率衰减。
|
1 2 3 |
# 学习率衰减 def decay_lrate(initial_lrate, decay, iteration): return initial_lrate * (1.0 / (1.0 + decay * iteration)) |
我们可以使用此函数通过不同的衰减值计算多个更新的学习率。
我们将比较一系列衰减值 [1E-1, 1E-2, 1E-3, 1E-4],初始学习率为 0.01,更新次数为 200。
|
1 2 3 4 5 6 7 8 |
decays = [1E-1, 1E-2, 1E-3, 1E-4] lrate = 0.01 n_updates = 200 for decay in decays: # 计算更新的学习率 lrates = [decay_lrate(lrate, decay, i) for i in range(n_updates)] # 绘制结果 pyplot.plot(lrates, label=str(decay)) |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 演示衰减对学习率的影响 from matplotlib import pyplot # 学习率衰减 def decay_lrate(initial_lrate, decay, iteration): return initial_lrate * (1.0 / (1.0 + decay * iteration)) decays = [1E-1, 1E-2, 1E-3, 1E-4] lrate = 0.01 n_updates = 200 for decay in decays: # 计算更新的学习率 lrates = [decay_lrate(lrate, decay, i) for i in range(n_updates)] # 绘制结果 pyplot.plot(lrates, label=str(decay)) pyplot.legend() pyplot.show() |
运行示例将创建一个显示不同衰减值在更新过程中学习率的折线图。
我们可以看到,在所有情况下,学习率都从初始值 0.01 开始。我们可以看到,较小的衰减值 1E-4(红色)几乎没有影响,而较大的衰减值 1E-1(蓝色)则产生显著影响,在 50 个轮次内将学习率降低到 0.002 以下(比初始值低约一个数量级),并最终达到约 0.0004 的值(比初始值低约两个数量级)。
我们可以看到,学习率的变化不是线性的。我们还可以看到,学习率的变化取决于批次大小,更新是在批次大小之后执行的。在前一节的示例中,每轮 500 个样本的默认批次大小为 32,导致每轮更新 16 次,在 200 轮中更新 3,200 次。
使用 0.1 的衰减率和 0.01 的初始学习率,我们可以计算出最终学习率是一个非常小的值,约为 3.1E-05。

学习率随多个权重更新变化的衰减效应折线图
我们可以更新前一节的示例来评估不同学习率衰减值的动态。
将学习率固定为 0.01 且不使用动量,我们预计会偏好非常小的学习率衰减,因为大的学习率衰减会迅速导致学习率过小,模型无法有效学习。
可以更新 `fit_model()` 函数以接受“decay”参数,该参数可用于配置 SGD 类的衰减。
该函数的更新版本如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 拟合模型并绘制学习曲线 def fit_model(trainX, trainy, testX, testy, decay): # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # 编译模型 opt = SGD(lr=0.01, decay=decay) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) # 绘制学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.title('decay='+str(decay), pad=-80) |
我们可以评估相同的四个衰减值 [1E-1, 1E-2, 1E-3, 1E-4] 及其对模型准确率的影响。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# blobs 问题上衰减率对准确率的研究 from sklearn.datasets import make_blobs from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from keras.utils import to_categorical from matplotlib import pyplot # 准备训练和测试数据集 def prepare_data(): # 生成 2d 分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 对输出变量进行独热编码 y = to_categorical(y) # 分割为训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] return trainX, trainy, testX, testy # 拟合模型并绘制学习曲线 def fit_model(trainX, trainy, testX, testy, decay): # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # 编译模型 opt = SGD(lr=0.01, decay=decay) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) # 绘制学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.title('decay='+str(decay), pad=-80) # 准备数据集 trainX, trainy, testX, testy = prepare_data() # 为不同的衰减率创建学习曲线 decay_rates = [1E-1, 1E-2, 1E-3, 1E-4] for i in range(len(decay_rates)): # 确定绘图编号 plot_no = 220 + (i+1) pyplot.subplot(plot_no) # 拟合模型并绘制特定衰减率的学习曲线 fit_model(trainX, trainy, testX, testy, decay_rates[i]) # 显示学习曲线 pyplot.show() |
运行示例将创建一个包含四个不同评估学习率衰减值的折线图的单个图形。训练数据集上的分类准确率用蓝色标记,测试数据集上的准确率用橙色标记。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑运行示例几次并比较平均结果。
我们可以看到,对于这个问题,大的衰减值 1E-1 和 1E-2 确实会过快地衰减学习率,并导致性能不佳。较小的衰减值确实能带来更好的性能,而 1E-4 的值可能导致与不使用衰减类似的结果。事实上,我们可以计算出衰减为 1E-4 时的最终学习率约为 0.0075,仅略低于初始值 0.01。
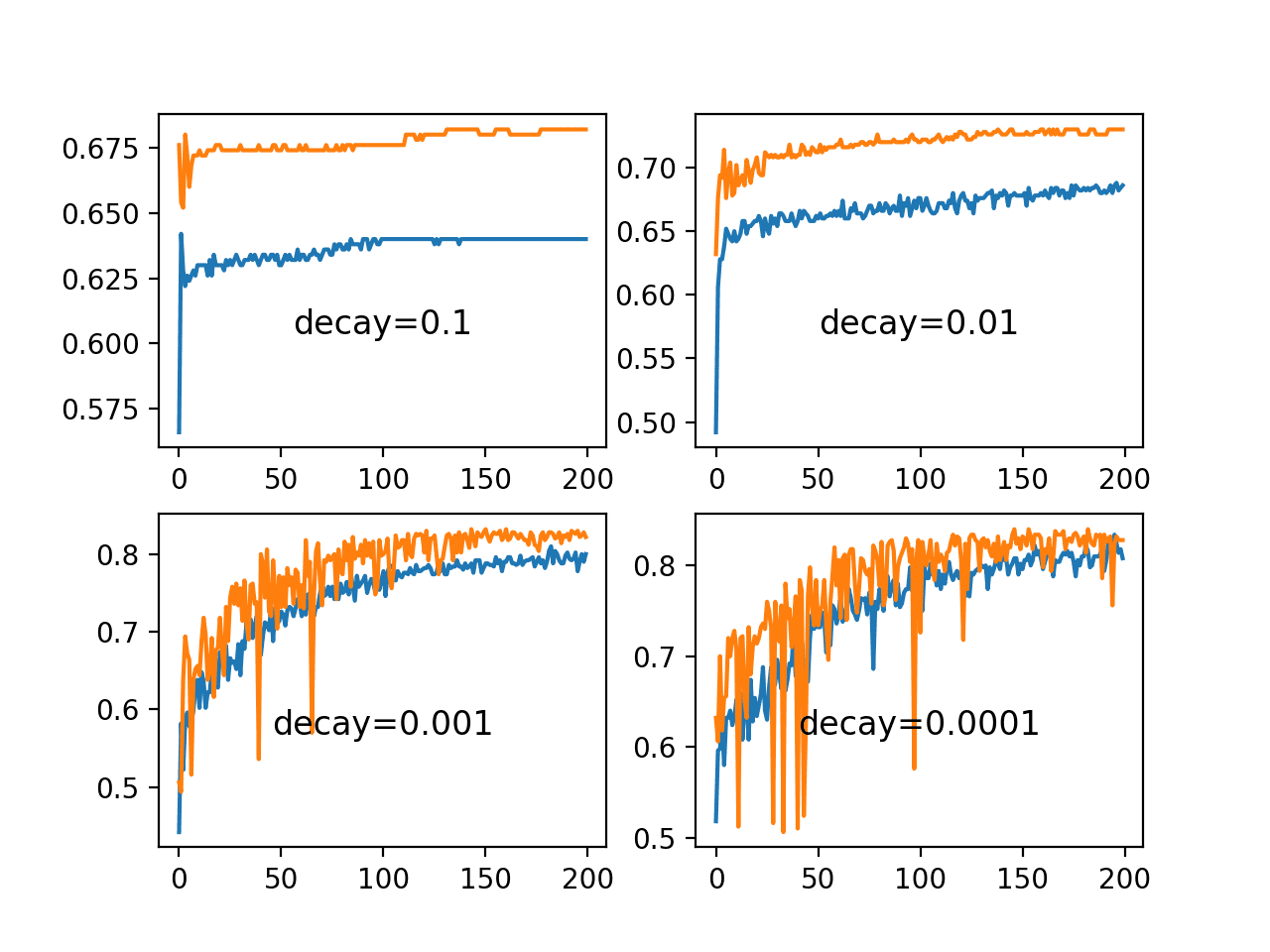
Blobs 分类问题上一系列衰减率对训练和测试准确率的折线图
学习率在平台期时下降
`ReduceLROnPlateau` 会在给定的轮次数内,当监控指标没有变化时,将学习率乘以一个因子来降低。
我们可以探索不同的“patience”值(即等待变化发生然后降低学习率的轮次数)的影响。我们将使用默认学习率 0.01,并将学习率降低一个数量级,方法是将“factor”参数设置为 0.1。
|
1 |
rlrp = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=patience, min_delta=1E-7) |
查看训练轮次中学习率的变化将很有趣。我们可以通过创建一个新的 Keras 回调函数来实现这一点,该函数负责在每个训练轮次结束时记录学习率。然后,我们可以检索记录的学习率并创建一个折线图,以查看学习率是如何受到下降的影响的。
我们可以创建一个自定义的 `Callback`,名为 `LearningRateMonitor`。`on_train_begin()` 函数在训练开始时调用,我们可以在其中定义一个空列表来存储学习率。`on_epoch_end()` 函数在每个训练轮次结束时调用,我们可以在其中从优化器中检索当前学习率并将其存储在列表中。完整的 `LearningRateMonitor` 回调函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 监控学习率 class LearningRateMonitor(Callback): # 训练开始 def on_train_begin(self, logs={}): self.lrates = list() # 结束每个训练轮次 def on_epoch_end(self, epoch, logs={}): # 获取并存储学习率 optimizer = self.model.optimizer lrate = float(backend.get_value(self.model.optimizer.lr)) self.lrates.append(lrate) |
前面几节开发的 `fit_model()` 函数可以更新,以创建和配置 `ReduceLROnPlateau` 回调函数以及我们新的 `LearningRateMonitor` 回调函数,并将它们与模型一起注册到 fit 调用中。
该函数还将接受“patience”作为参数,以便我们可以评估不同的值。
|
1 2 3 4 |
# 拟合模型 rlrp = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=patience, min_delta=1E-7) lrm = LearningRateMonitor() history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0, callbacks=[rlrp, lrm]) |
为了在本例中创建几个图,`fit_model()` 函数将返回学习率列表,以及每个训练轮次的训练数据集上的损失和准确率,而不是直接创建子图。
带有这些更新的函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 拟合模型并绘制学习曲线 def fit_model(trainX, trainy, testX, testy, patience): # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # 编译模型 opt = SGD(lr=0.01) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 rlrp = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=patience, min_delta=1E-7) lrm = LearningRateMonitor() history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0, callbacks=[rlrp, lrm]) return lrm.lrates, history.history['loss'], history.history['accuracy'] |
`ReduceLROnPlateau` 中的耐心度控制着学习率会多久被降低一次。
我们将测试几个适合此模型在 blobs 问题上的耐心值,并跟踪每次运行的学习率、损失和准确率系列。
|
1 2 3 4 5 6 7 8 9 |
# 为不同的耐心值创建学习曲线 patiences = [2, 5, 10, 15] lr_list, loss_list, acc_list, = list(), list(), list() for i in range(len(patiences)): # 拟合模型并绘制特定耐心值学习曲线 lr, loss, acc = fit_model(trainX, trainy, testX, testy, patiences[i]) lr_list.append(lr) loss_list.append(loss) acc_list.append(acc) |
在运行结束时,我们将为每个耐心值绘制学习率、训练损失和训练准确率的折线图。
我们可以创建一个辅助函数,轻松地为我们记录的每个系列创建带有子图的图形。
|
1 2 3 4 5 6 7 |
# 为一个系列创建折线图 def line_plots(patiences, series): for i in range(len(patiences)): pyplot.subplot(220 + (i+1)) pyplot.plot(series[i]) pyplot.title('patience='+str(patiences[i]), pad=-80) pyplot.show() |
将这些元素联系起来,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
# 研究耐心对学习率下降策略在blobs问题上的影响 from sklearn.datasets import make_blobs from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from keras.utils import to_categorical from keras.callbacks import Callback from keras.callbacks import ReduceLROnPlateau from keras import backend from matplotlib import pyplot # 监控学习率 class LearningRateMonitor(Callback): # 训练开始 def on_train_begin(self, logs={}): self.lrates = list() # 结束每个训练轮次 def on_epoch_end(self, epoch, logs={}): # 获取并存储学习率 optimizer = self.model.optimizer lrate = float(backend.get_value(self.model.optimizer.lr)) self.lrates.append(lrate) # 准备训练和测试数据集 def prepare_data(): # 生成 2d 分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 对输出变量进行独热编码 y = to_categorical(y) # 分割为训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] return trainX, trainy, testX, testy # 拟合模型并绘制学习曲线 def fit_model(trainX, trainy, testX, testy, patience): # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # 编译模型 opt = SGD(lr=0.01) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 rlrp = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=patience, min_delta=1E-7) lrm = LearningRateMonitor() history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0, callbacks=[rlrp, lrm]) return lrm.lrates, history.history['loss'], history.history['accuracy'] # 为一个系列创建折线图 def line_plots(patiences, series): for i in range(len(patiences)): pyplot.subplot(220 + (i+1)) pyplot.plot(series[i]) pyplot.title('patience='+str(patiences[i]), pad=-80) pyplot.show() # 准备数据集 trainX, trainy, testX, testy = prepare_data() # 为不同的耐心值创建学习曲线 patiences = [2, 5, 10, 15] lr_list, loss_list, acc_list, = list(), list(), list() for i in range(len(patiences)): # 拟合模型并绘制特定耐心值学习曲线 lr, loss, acc = fit_model(trainX, trainy, testX, testy, patiences[i]) lr_list.append(lr) loss_list.append(loss) acc_list.append(acc) # 绘制学习率 line_plots(patiences, lr_list) # 绘制损失 line_plots(patiences, loss_list) # 绘制准确率 line_plots(patiences, acc_list) |
运行示例将创建三个图形,每个图形都包含不同耐心值对应的折线图。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑运行示例几次并比较平均结果。
第一个图形显示了在每个评估的耐心值下,学习率随训练周期变化的折线图。我们可以看到,耐心值为2时,学习率在25个周期内迅速下降到最小值;而耐心值为15时,学习率仅下降了一次。
从这些图中,我们可以预期耐心值为5和10对于此模型在此问题上会产生更好的性能,因为它们允许在降低学习率以细化权重之前,较大的学习率能被使用一段时间。
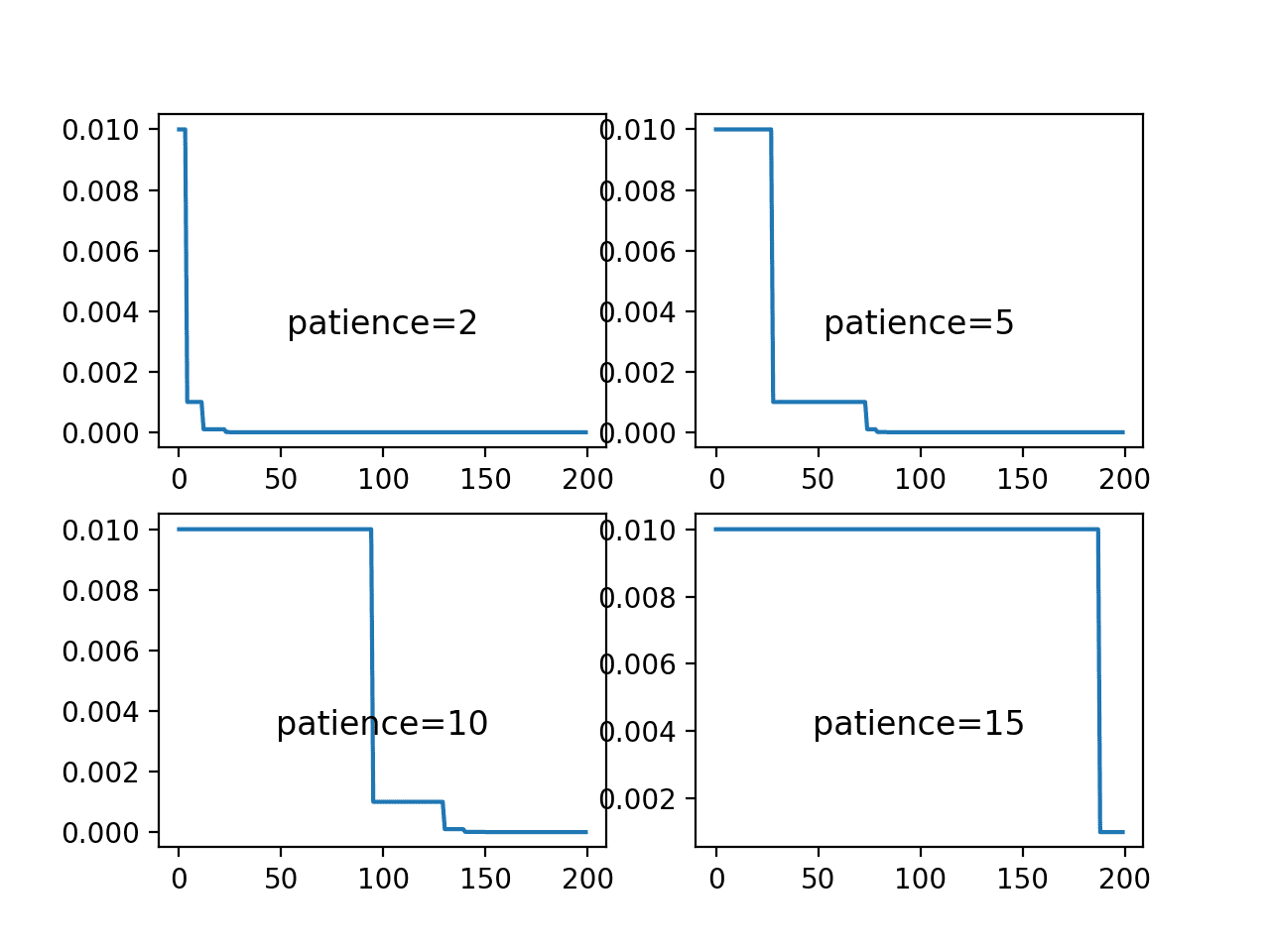
学习率在ReduceLROnPlateau调度中不同耐心值下的周期变化折线图
下一个图形显示了训练数据集上每个耐心值的损失。
该图显示,耐心值为2和5时,模型收敛速度很快,但可能收敛到一个次优的损失值。对于耐心值为10和15的情况,损失下降得相当合理,直到学习率下降到一个较大的变化就难以看到的水平。对于耐心值为10,这种情况发生在训练中期;对于耐心值为15,则接近训练结束。
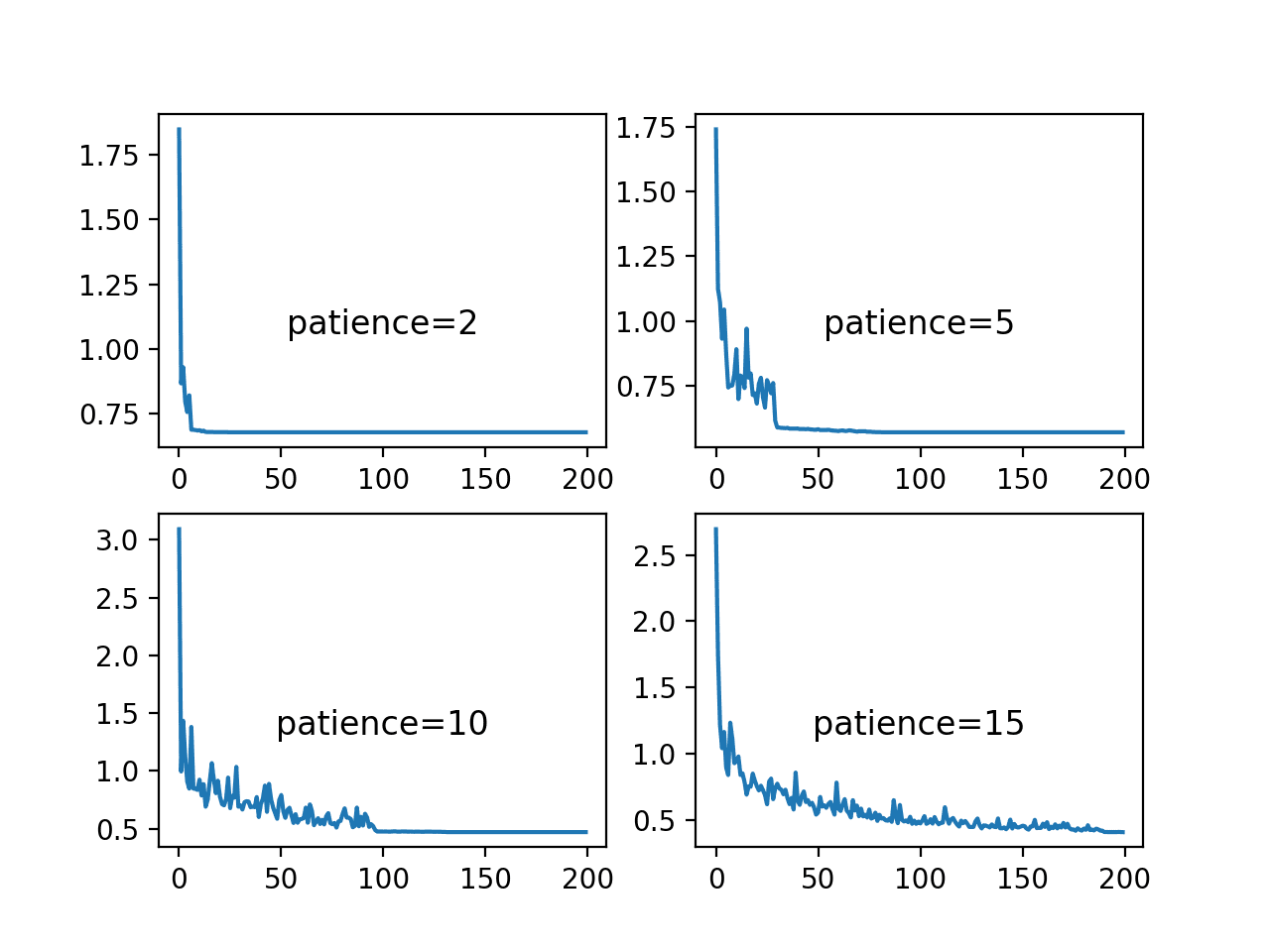
训练损失在ReduceLROnPlateau调度中不同耐心值下的周期变化折线图
最后一个图形显示了每个耐心值下的训练集准确率随训练周期变化的情况。
我们可以看到,实际上,耐心值为2和5个周期时,模型过早收敛,导致模型性能不佳,准确率分别约为65%和低于75%。耐心值越大,模型性能越好,其中耐心值为10的模型在150个周期前收敛,而耐心值为15的模型由于学习率几乎没有变化,准确率表现出一定的波动性。
这些图显示了如何以一种适合问题和模型配置的方式降低学习率,可以带来熟练且收敛稳定的最终权重,这是训练结束时最终模型的一个理想属性。
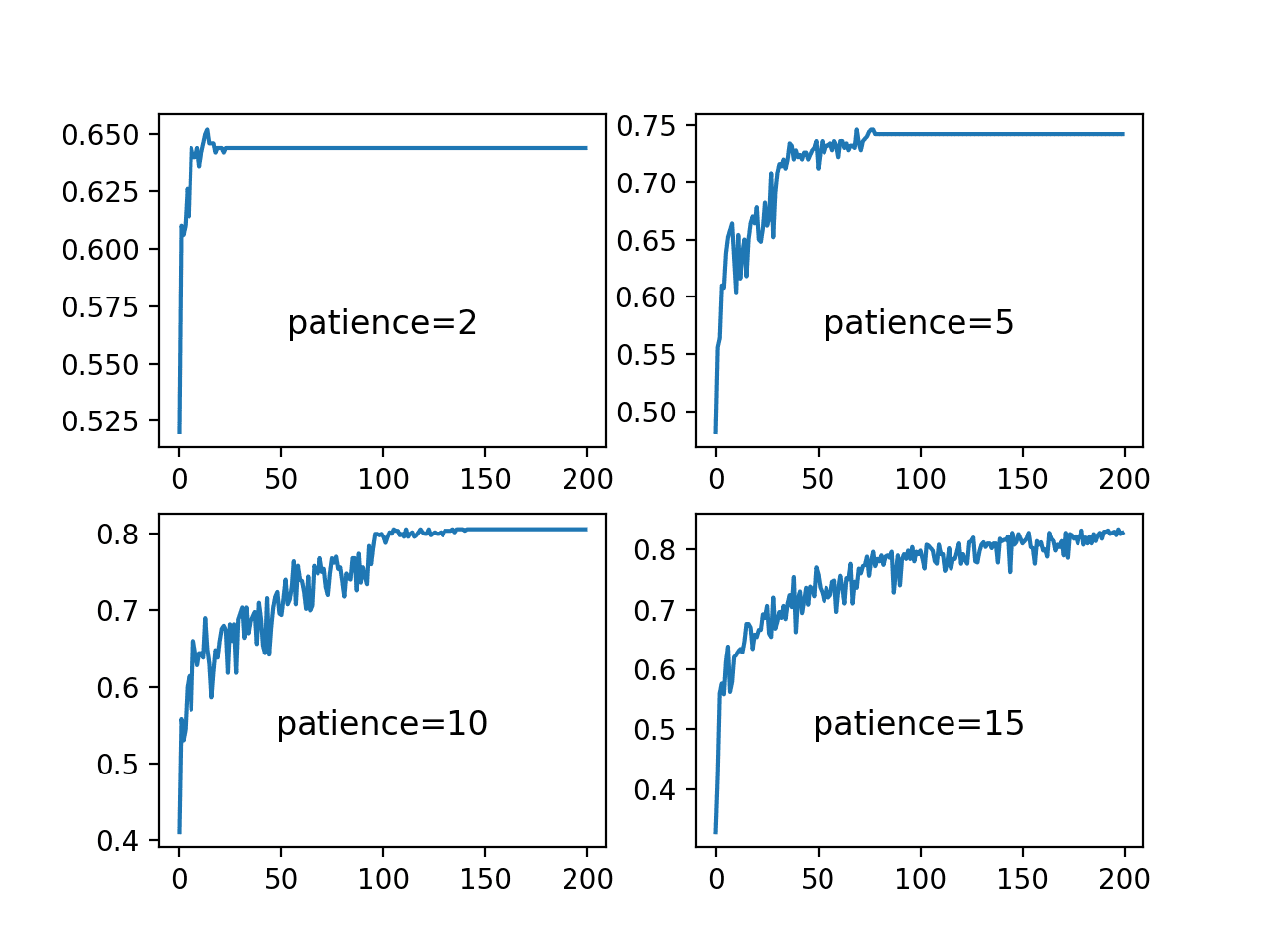
训练准确率在ReduceLROnPlateau调度中不同耐心值下的周期变化折线图
自适应学习率的影响
学习率和学习率调度都难以配置,并且对深度学习神经网络模型的性能至关重要。
Keras提供了许多流行的自适应学习率的随机梯度下降变体,例如
- 自适应梯度算法 (AdaGrad)。
- 均方根传播 (RMSprop)。
- 自适应矩估计 (Adam)。
每种方法都提供了不同的方法来为网络中的每个权重自适应学习率。
没有一种单一的最佳算法,在某个问题上对优化算法进行竞赛的结果不太可能转移到新问题上。
我们可以研究不同的自适应学习率方法在blobs问题上的动态。 `fit_model()` 函数可以更新为接受一个要评估的优化算法的名称,该名称可以在编译MLP模型时通过 “`optimizer`” 参数指定。然后将使用每种方法的默认参数。下面列出了该函数的更新版本。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 拟合模型并绘制学习曲线 def fit_model(trainX, trainy, testX, testy, optimizer): # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # 编译模型 model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) # 绘制学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.title('opt='+optimizer, pad=-80) |
我们可以探索RMSprop、AdaGrad和Adam这三种流行的方法,并将它们的行为与具有静态学习率的简单随机梯度下降进行比较。
我们期望自适应学习率版本的算法表现相似或更好,也许能在更少的训练周期内适应问题,但重要的是,能产生一个更稳定的模型。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 准备数据集 trainX, trainy, testX, testy = prepare_data() # 为不同的优化器创建学习曲线 momentums = ['sgd', 'rmsprop', 'adagrad', 'adam'] for i in range(len(momentums)): # 确定绘图编号 plot_no = 220 + (i+1) pyplot.subplot(plot_no) # 为优化器拟合模型并绘制学习曲线 fit_model(trainX, trainy, testX, testy, momentums[i]) # 显示学习曲线 pyplot.show() |
将这些元素联系起来,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
# 研究sgd在blobs问题上的自适应学习率 from sklearn.datasets import make_blobs from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from keras.utils import to_categorical from keras.callbacks import Callback from keras import backend from matplotlib import pyplot # 准备训练和测试数据集 def prepare_data(): # 生成 2d 分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 对输出变量进行独热编码 y = to_categorical(y) # 分割为训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] return trainX, trainy, testX, testy # 拟合模型并绘制学习曲线 def fit_model(trainX, trainy, testX, testy, optimizer): # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # 编译模型 model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) # 绘制学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.title('opt='+optimizer, pad=-80) # 准备数据集 trainX, trainy, testX, testy = prepare_data() # 为不同的优化器创建学习曲线 momentums = ['sgd', 'rmsprop', 'adagrad', 'adam'] for i in range(len(momentums)): # 确定绘图编号 plot_no = 220 + (i+1) pyplot.subplot(plot_no) # 为优化器拟合模型并绘制学习曲线 fit_model(trainX, trainy, testX, testy, momentums[i]) # 显示学习曲线 pyplot.show() |
运行示例将创建一个图形,其中包含四种不同优化算法的折线图。训练数据集上的分类准确率用蓝色标记,而测试数据集上的准确率用橙色标记。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑运行示例几次并比较平均结果。
同样,我们可以看到,学习率为0.01且没有动量的SGD确实能解决问题,但需要近200个周期,并且在训练数据上的准确率波动很大,在测试数据集上更是如此。图表显示,所有三种自适应学习率方法都能更快地解决问题,并且在训练和测试集准确率上的波动性大大降低。
RMSProp和Adam都表现出相似的性能,在50个训练周期内有效地解决了问题,并将剩余的训练时间用于进行非常小的权重更新,但没有像我们在上一节的学习率调度中看到的那样收敛。
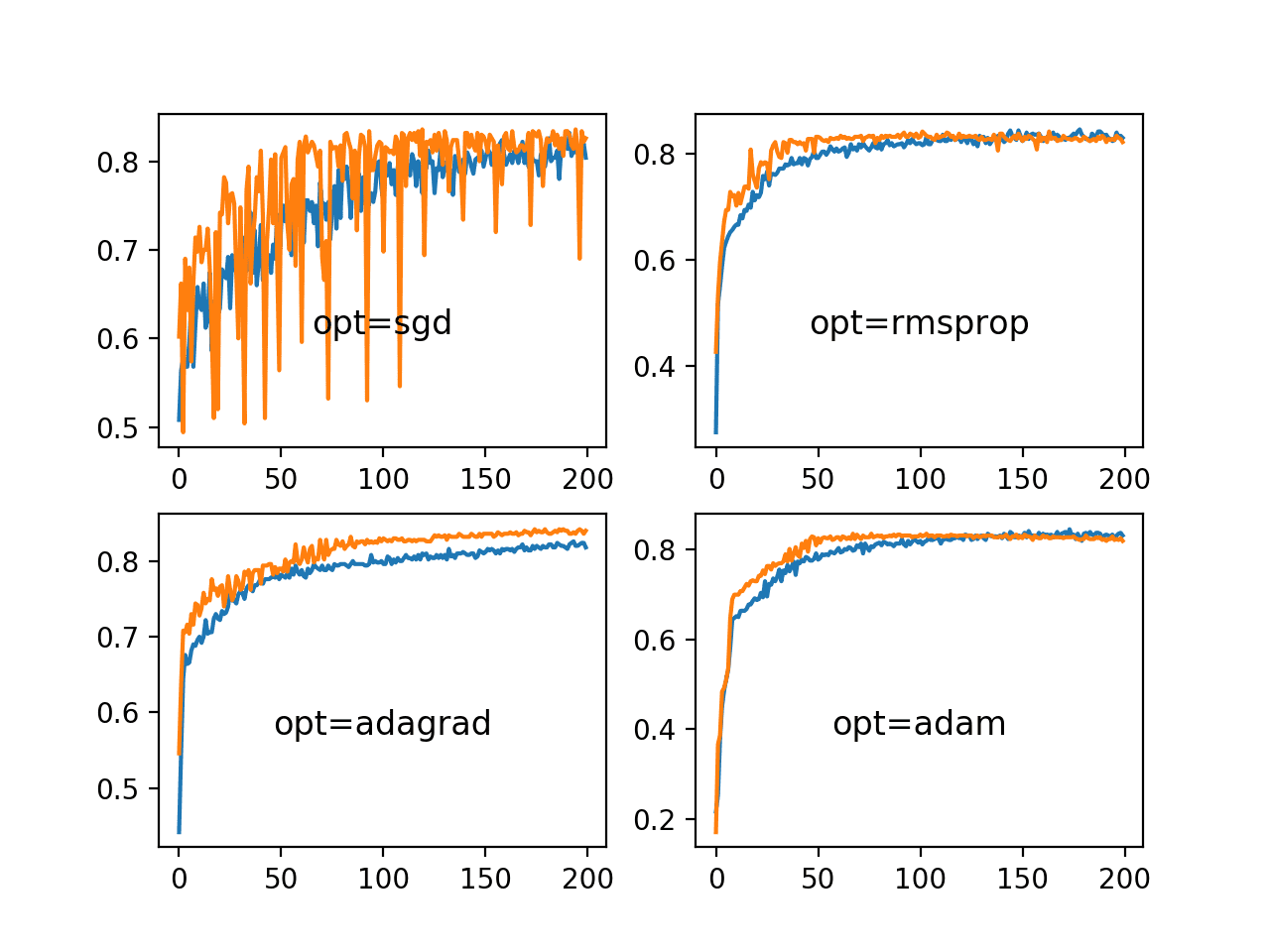
在blobs分类问题上,一系列自适应学习率方法的训练集和测试集准确率折线图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
文章
论文
- 深度架构基于梯度的训练的实用建议, 2012.
书籍
- 第8章:深度模型训练的优化,深度学习,2016。
- 第6章:学习率和动量,神经网制造:前馈人工神经网络中的监督学习,1999。
- 第5.7节:梯度下降,模式识别神经网络,1995。
API
文章
总结
在本教程中,您了解了学习率、学习率调度和自适应学习率对模型性能的影响。
具体来说,你学到了:
- 高学习率会导致训练不稳定,而极小的学习率会导致训练失败。
- 动量可以加速训练,而学习率调度可以帮助优化过程收敛。
- 自适应学习率可以加速训练,并减轻选择学习率和学习率调度的一些压力。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





感谢您的帖子,我有一个问题。我使用adam作为优化器,并使用LearningRateMonitor CallBack记录每个周期的lr。结果始终是0.001。这是因为adam对模型的每个参数都是自适应的吗?
正确。
那是否意味着当我们使用adam作为优化器时,我们无法记录学习率的变化?
正确。使用SGD。
亲爱的Jason Brownlee博士,
拜读您的博客是件多么令人愉快的事情。您的内容非常信息丰富且有用。非常感谢您的辛勤工作。
我有一个关于自适应优化器的问题。正如您所说,最好使用SGD来评估我们模型上的最佳学习率(lr)。在这种情况下,例如,如果我使用SGD找到了$lr = 0.01$,并且我发现Adagrad是我的模型的最佳优化器,那是否意味着我应该使用$Adagrad$和$lr = 0.01$。如果是这样,我想知道为什么我们需要为自适应优化器定义学习率,因为它们本应是自适应的。
我期待您的回复。
非常感谢
Adagrad需要有一个初始学习率。它对学习率不那么敏感,但并非完全不敏感。在这种情况下,您可能会发现改变学习率对结果有轻微影响。
一如既往,非常棒的教程,Jason。
您能否写一篇关于使用“hpsklearn”和/或hyperopt进行超参数调优的博文?
那将是太棒了!
谢谢。
很好的建议,谢谢。
精彩的帖子Jason,谢谢!
对Adam等自适应学习率衰减方法进行学习率衰减是否有意义或可期待性能有所提高?
谢谢。
不是很必要,因为每个权重都有自己的学习率。
Jason!帖子又一次很棒,在运行代码时
from sklearn.datasets.samples_generator from keras.layers import Dense
我遇到了一个错误
File “”, line 2
from sklearn.datasets.samples_generator from keras.layers import Dense
^
SyntaxError: invalid syntax
谢谢。
也许请仔细检查您是否复制了所有代码,并且缩进正确。
我们不能改变Adam和Rmsprop的学习率和动量,对吗?它们是否意味着是预定义的和固定的?我只想知道它们是否会根据模型进行自适应?
我们可以为这些自适应学习率方法设置初始学习率。
嗨,Jason,
您有没有考虑过开始写关于强化学习的内容?
此致,
是的,请看这个
https://machinelearning.org.cn/faq/single-faq/do-you-have-tutorials-on-deep-reinforcement-learning
先生,如何将结果显示在单个图中,而不是显示在各种子图中?
您可以使用pyplot.plot()
先生,请提供在单个图上绘制各种优化器的代码
感谢您的建议。
当学习率衰减10倍(例如,在训练CIFAR-10 ResNet时),准确率会突然增加。您能否告诉我学习率衰减时权重到底发生了什么?例如,人们会认为步长在减小,所以权重变化得更慢。但同时,梯度值可能迅速增加(因为损失在学习率衰减之前趋于平稳——这意味着训练过程可能处于某种局部最小值或鞍点;因此,梯度值会很小,损失会在某个值周围振荡)。那么,我的问题是,当学习率衰减10倍时,CNN权重是快速变化还是缓慢变化??
谢谢。任何想法都将非常感激!
当学习率衰减时,对模型权重的更新会减少——这很简单。
当您说10倍时,您是指10的因子吗?
如果您从0.001中减去10,您将得到一个很大的负数,这对于学习率来说是一个坏主意。
感谢您的回复。我当然指的是10的因子。
学习率的衰减意味着对权重和模型性能的改变会减小。
先生,请提供用于单个图的各种子图代码
感谢您的建议。
感谢您提供的精彩教程!您能否解释一下在使用ReduceLROnPlateau时如何选择要监控的指标?例如,监控val_loss与val_acc有什么优缺点?谢谢!
几乎总是验证损失。
我们直接最小化损失,而val loss提供了样本外性能的 ধারণা (dilemma)。
谢谢Jason!您是否也推荐EarlyStopping和ModelCheckpoint?当val_loss一段时间没有改善时停止,并恢复到val_loss最佳的那个周期?
在大多数情况下
https://machinelearning.org.cn/early-stopping-to-avoid-overtraining-neural-network-models/
我很欣赏您的博客。谢谢,Mark
谢谢!
只是一个拼写建议:我认为“权重衰减”应改为“学习率衰减”。
谢谢你的文章!
谢谢,已修复!
你好,很棒的博客,谢谢。我有一个问题。您在for循环中初始化模型为model = Sequential。这足够初始化吗?为什么不使用keras.backend.clear_session()来清除后端的一切?
我不认为有必要。
你好,感谢这篇精彩的文章。学到了很多!
请在“学习率调度”部分下面的一行中进行一次小拼写修正。
节。
“model.fig(…, callbacks=[rlrop])”
谢谢,已修复!
您是否有关于为keras NN指定用户定义成本函数的教程,我特别想了解您如何将其呈现给系统。
抱歉,我没有。
这会根据自定义指标为您提供思路
https://machinelearning.org.cn/custom-metrics-deep-learning-keras-python/
有趣的链接,我遇到的一个自定义损失函数的问题是,自定义损失函数需要张量作为其数据,而我对如何表示张量数据不熟悉,但您的文章建议您使用“backend”让keras以某种方式进行转换?
是的,您可以使用后端函数来操作张量。
我会试试
import tensorflow.keras.backend as K
import numpy as np
a = np.array([1,2,3])
b = K.constant(a)
print(b)
#
print(K.eval(b))
# array([1., 2., 3.], dtype=float32)
祝你好运!
CNN优化器的学习率为0.0001,对应的批次大小为16,训练时间效率为1.82毫秒。对于RNN,学习率为0.001,批次大小为1,时间效率?
有人能说出RNN的时间效率吗,其中学习率为0.001,批次大小为一
RNN效率不高,但能力通常更强。
好帖子,先生!
它非常有解释性。
注意到`LearningRateScheduler`代码块中的函数缺少冒号。
谢谢
Peter。
谢谢!
已修复拼写错误。
好帖子!
在使用Adam时,在模型达到平台期后改变学习率以查看是否有更好的性能是否合法或推荐?
例如,如果模型以lr=0.001开始,并在200个周期后收敛到某个点。然后,用较低的学习率重新编译模型,加载最佳权重,然后再次运行模型以查看可以获得什么。
不。Adam会为您自适应学习率。这就是该方法的好处。
章节:学习率衰减
以下一行中的高亮词
我们可以看到,1E-1和1E-2的较大衰减值确实对该模型在该问题上的学习率衰减过快,导致性能不佳。**较大的**衰减值确实带来了更好的性能,衰减值为1E-4可能导致与不使用衰减类似的结果。事实上,我们可以计算出衰减为1E-4的最终学习率约为0.0075,仅比初始值0.01略小。
这里有一个拼写错误:**较大的**必须改为“较小的”。
请修正。
谢谢,已修正。
Jason,
我们是否成比例地减少LR并增加epoch,就像我们在集成模型中处理树的数量和LR一样?作为概述…
这可能有帮助。不一定。在您的模型/数据上尝试一下,看看是否有帮助。
嗨,Jason,
非常感谢您的好文章。
学习率衰减是一种正则化技术吗?如果是,如何实现?
谢谢!
不完全是,它减慢了学习速度,但我不会将其视为一种正则化技术本身。
非常感谢您的耐心回复。那Reduce Learning rate on Plateau呢?
关于它?您是指如何做到,还是指它是否是一种正则化方法?
嗨,Jason,
我的意思是,您是否会将Reduce Learning rate on Plateau视为一种正则化方法?
谢谢!
是的,我想是的。
精彩的博客,谢谢!
不客气!
这句话“学习率过大可能导致模型过快收敛到次优解,而学习率过小可能导致过程陷入停滞。”是错误的。
当学习率设置得过高时,算法可能会越过最小值并在其周围振荡,甚至发散。这意味着算法可能根本无法收敛,更不用说收敛到次优解了。
感谢您的反馈Hussein!