
使用Python理解机器学习中的概率分布
图片来源:编辑 | Midjourney
在机器学习中,概率分布发挥着至关重要的作用,原因如下:为信息和数据的不确定性建模,在随机环境中应用优化过程,以及执行推理过程,仅举几例。因此,理解概率分布在机器学习中的作用和用途,对于设计稳健的机器学习模型、选择正确的算法以及解释概率性质的输出至关重要,尤其是在使用Python等机器学习友好型编程语言构建模型时。
本文介绍了与机器学习相关的关键概率分布,探讨了它们在不同机器学习任务中的应用,并提供了实用的Python实现,以帮助从业者有效地应用这些概念。建议具备最常见概率分布的基础知识,以便充分利用本文。
机器学习的关键概率分布
在众多现有的离散和连续概率分布中,以下分布因其在知名机器学习模型和算法中的相关性和基础性而脱颖而出。
- 正态(高斯)分布用于对线性回归模型、朴素贝叶斯模型和变分自编码器(VAE)等生成模型中的训练残差进行建模。Python的SciPy和NumPy库通过
scipy.stats.norm和numpy.random.normal组件来实现它们。 - 在逻辑回归中,当分类输出为二元时,伯努利分布和二项分布会与交叉熵损失函数一起用于训练算法。它们都可以用Python中的
scipy.stats.bernoulli和scipy.stats.binom来使用。 - 泊松分布和指数分布能够对随时间发生的事件进行建模,对于为强化学习算法中的随机奖励建模很有用。在Python中,可以通过使用
scipy.stats.poisson, scipy.stats.expon来调用它们。 - 基于朴素贝叶斯的文本分类模型使用多项分布和狄利克雷分布来解释模型所依赖的推理过程中的后验概率。在Python中,利用这些分布的最佳伙伴是
scipy.stats.beta, sklearn.mixture.GaussianMixture。
在机器学习中利用概率分布(使用Python)
现在,让我们来看一些易于理解的示例,说明概率分布如何在机器学习模型构建生命周期的特定方面“扮演不同角色”。
首先,当我们需要生成随机样本来构建或测试机器学习模型时,概率分布是无价的。它们可用于合成生成数据属性,例如遵循正态分布,这对于测试模型、缩放不成比例的特征或检测异常非常有用。
例如,生成500个正态分布样本可以像这样简单:
|
1 2 |
import numpy as np data = np.random.normal(loc=0, scale=1, size=500) |
将概率分布拟合到数据集——换句话说,在假设特定分布的情况下估计数据集的均值(mu)和方差(sigma)——是贝叶斯分析和推理中的一个关键过程,可以按如下方式实现:
|
1 2 |
from scipy import stats mu, sigma = stats.norm.fit(data) |
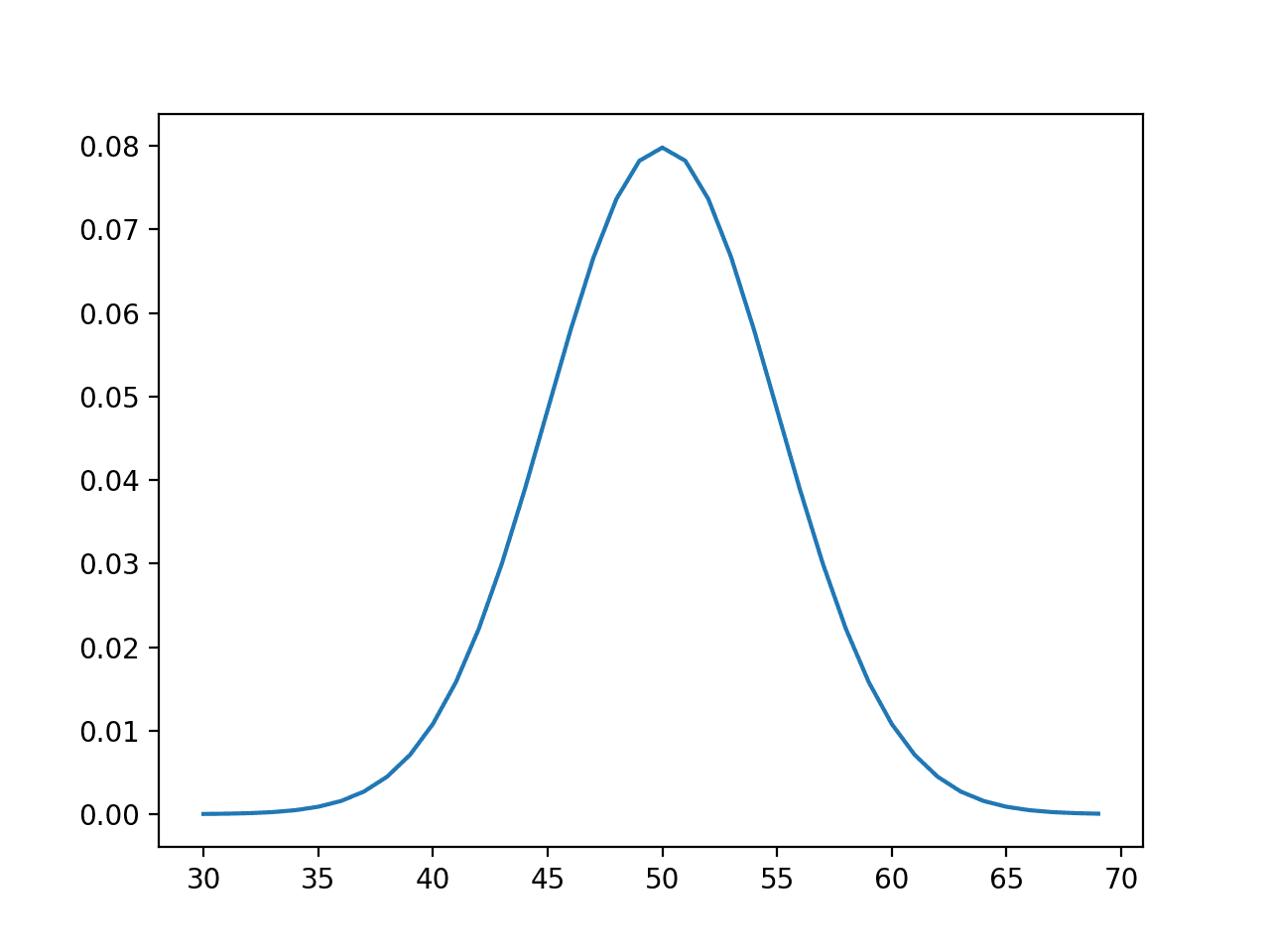
数据可视化是机器学习中另一个强大且富有洞察力的过程,用于确定数据集是否遵循某个特定分布,然后再做出可能在机器学习开发生命周期的其他阶段所需的诸如正态性之类的假设。它还可以帮助检测偏度和其他统计现象。
本示例生成一个直方图,用于分析和解释先前生成数据集的分布。添加的KDE选项包含一个核密度估计曲线,用于查看直方图的平滑版本,从而更容易检测底层概率分布。
|
1 2 3 4 5 6 |
import seaborn as sns import matplotlib.pyplot as plt sns.histplot(data, kde=True) plt.title("带有核密度估计(KDE)曲线的数据分布") plt.show() |

数据集可视化和KDE曲线,用于分析其如何拟合概率分布
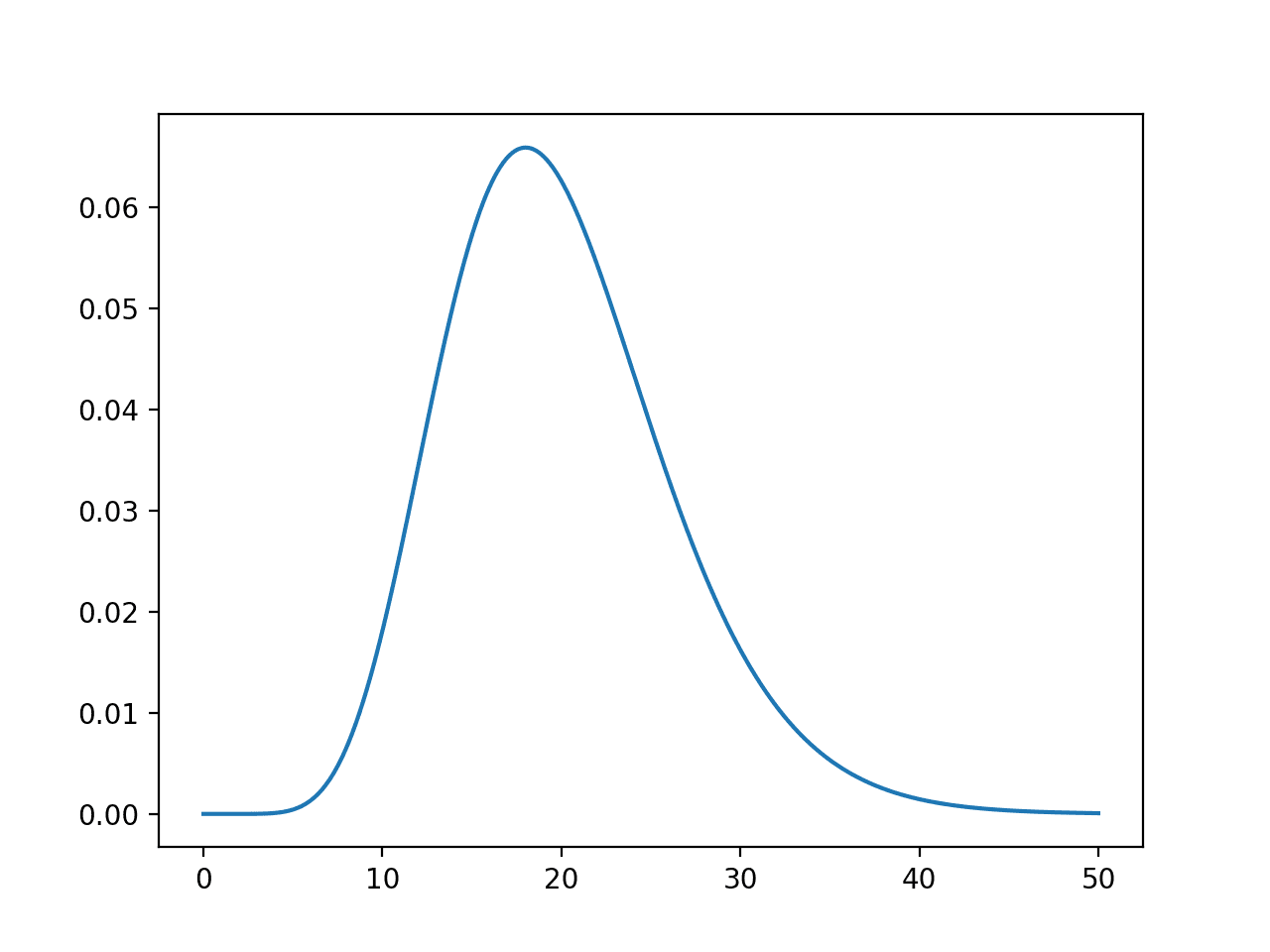
最后但同样重要的一点是,让我们展示一个在实践中与贝叶斯推理相关的分布。此代码说明了Beta分布。此分布也常用于A/B测试和一些强化学习方法。
最后一个示例生成100个在0到1之间均匀分布的数据点,并绘制与Beta分布相关的概率密度函数(PDF),其参数alpha和beta分别为2和5。这是一个右偏(向较小值倾斜)的Beta分布示例。
|
1 2 3 4 5 6 7 8 |
from scipy.stats import beta import numpy as np import matplotlib.pyplot as plt x = np.linspace(0, 1, 100) plt.plot(x, beta.pdf(x, 2, 5), label="Beta分布") plt.legend() plt.show() |

Beta分布常用于贝叶斯推理模型
概率分布在机器学习中的力量
概率分布不仅仅是学术上的抽象概念;它们是实用的工具,使我们能够在整个机器学习生命周期中对不确定性进行建模和管理。通过提供理解数据变异性的严格框架,这些分布使我们能够模拟真实世界的场景、校准模型输出,甚至指导算法选择。无论是用高斯分布对残差误差进行建模,还是利用Beta分布的偏斜特性进行贝叶斯推理,拥抱概率分布是开发可靠模型的关键。
概率分布背后的理论原则是经典统计学与现代机器学习技术之间的桥梁。它们通过提供对数据行为和不确定性估计的见解,为许多算法奠定了基础。例如,了解何时使用泊松分布或指数分布对于调整强化学习算法至关重要,而认识到偏斜或多峰分布的影响可以提高预测建模的准确性。理论与实践的这种相互作用不仅可以改进我们的模型,还可以加深我们对模型所基于的数据的理解。
此外,随着机器学习的不断发展,将概率推理整合到复杂模型中变得越来越关键。像VAE和贝叶斯神经网络这样的高级架构利用这些统计概念来学习复杂的数据表示并量化不确定性。概率建模与深度学习方法的这种融合,凸显了掌握概率分布的重要性——不仅作为数学工具,而且作为追求更具可解释性和适应性模型的重要组成部分。
总结
通过一些确定的分布、Python组件和示例,我们已经研究了概率分布在实现构建Python机器学习模型所依据的重要步骤和过程中的作用。最终,对概率分布的透彻掌握可以增强机器学习过程的每个阶段,从数据生成和假设检验到模型训练和推理。通过将本文讨论的理论见解与实际实现相结合,您可以更好地构建既具创新性又具韧性的模型。


暂无评论。