卷积神经网络在计算机视觉应用中取得了成功。人们提出了各种网络架构,它们既不神秘也不难理解。
在本教程中,您将了解卷积层的操作及其在更大的卷积神经网络中的作用。
完成本教程后,你将学到:
- 卷积层如何从图像中提取特征
- 不同的卷积层如何堆叠以构建神经网络
让我们开始吧。

理解卷积神经网络的设计
图片由 Kin Shing Lai 拍摄。保留部分权利。
概述
本文分为三个部分:
- 示例网络
- 展示特征图
- 卷积层的作用
示例网络
以下是在 CIFAR-10 数据集上进行图像分类的程序
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
import matplotlib.pyplot as plt import numpy as np import tensorflow as tf from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Conv2D, Dropout, MaxPooling2D, Flatten, Dense from tensorflow.keras.constraints import MaxNorm from tensorflow.keras.datasets.cifar10 import load_data (X_train, y_train), (X_test, y_test) = load_data() # 缩放图像 X_train_scaled = X_train / 255.0 X_test_scaled = X_test / 255.0 model = Sequential([ Conv2D(32, (3,3), input_shape=(32, 32, 3), padding="same", activation="relu", kernel_constraint=MaxNorm(3)), Dropout(0.3), Conv2D(32, (3,3), padding="same", activation="relu", kernel_constraint=MaxNorm(3)), MaxPooling2D(), Flatten(), Dense(512, activation="relu", kernel_constraint=MaxNorm(3)), Dropout(0.5), Dense(10, activation="sigmoid") ]) model.compile(optimizer="adam", loss="sparse_categorical_crossentropy", metrics="sparse_categorical_accuracy") model.fit(X_train_scaled, y_train, validation_data=(X_test_scaled, y_test), epochs=25, batch_size=32) |
该网络在分类中应该能够达到约70%的准确率。图像为32x32像素的RGB颜色。它们分为10个不同的类别,标签是0到9的整数。
您可以使用Keras的summary()函数打印网络结构
|
1 2 |
... model.summary() |
在该网络中,屏幕上将显示以下内容
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
模型: "sequential" _________________________________________________________________ 层 (类型) 输出形状 参数数量 ================================================================= conv2d (Conv2D) (None, 32, 32, 32) 896 dropout (Dropout) (None, 32, 32, 32) 0 conv2d_1 (Conv2D) (None, 32, 32, 32) 9248 max_pooling2d (MaxPooling2D) (None, 16, 16, 32) 0 ) flatten (Flatten) (None, 8192) 0 dense (Dense) (None, 512) 4194816 dropout_1 (Dropout) (None, 512) 0 dense_1 (Dense) (None, 10) 5130 ================================================================= 总参数: 4,210,090 可训练参数: 4,210,090 不可训练参数: 0 _________________________________________________________________ |
在图像分类网络中,通常在早期阶段包含卷积层,并交错使用 dropout 和池化层。然后,在后期阶段,卷积层的输出被展平并通过一些全连接层进行处理。
展示特征图
在上述网络中,有两个卷积层(`Conv2D`)。第一层定义如下:
|
1 |
Conv2D(32, (3,3), input_shape=(32, 32, 3), padding="same", activation="relu", kernel_constraint=MaxNorm(3)) |
这意味着卷积层将具有一个 3x3 的核,并应用于 32x32 像素和三个通道(RGB 颜色)的输入图像。因此,该层的输出将是 32 个通道。
为了理解卷积层,您可以查看其核。变量 `model` 保存了网络,您可以使用以下代码找到第一个卷积层的核:
|
1 2 |
... print(model.layers[0].kernel) |
输出如下:
|
1 2 3 4 5 6 7 8 |
<tf.Variable 'conv2d/kernel:0' shape=(3, 3, 3, 32) dtype=float32, numpy= array([[[[-2.30068922e-01, 1.41024575e-01, -1.93124503e-01, -2.03153938e-01, 7.71819279e-02, 4.81446862e-01, -1.11971676e-01, -1.75487325e-01, -4.01797555e-02, ... 4.64215249e-01, 4.10646647e-02, 4.99733612e-02, -5.22711873e-02, -9.20209661e-03, -1.16479330e-01, 9.25614685e-02, -4.43541892e-02]]]], dtype=float32)> |
通过将上述输出中的名称 `conv2d` 与 `model.summary()` 的输出进行比较,您可以判断 `model.layers[0]` 是正确的层。该层的核形状为 `(3, 3, 3, 32)`,分别表示高度、宽度、输入通道和输出特征图。
假设核是一个 NumPy 数组 `k`。卷积层将取其核 `k[:, :, 0, n]`(一个 3x3 数组)并应用于图像的第一个通道。然后将 `k[:, :, 1, n]` 应用于图像的第二个通道,依此类推。之后,所有通道上的卷积结果相加,成为输出的特征图 `n`,其中 `n` 在本例中将从 0 运行到 31,用于 32 个输出特征图。
在 Keras 中,您可以使用提取器模型提取每一层的输出。在以下代码中,您将创建一个包含一个输入图像的批次,并将其发送到网络。然后查看第一个卷积层的特征图:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
... # 提取每一层的输出 extractor = tf.keras.Model(inputs=model.inputs, outputs=[layer.output for layer in model.layers]) features = extractor(np.expand_dims(X_train[7], 0)) # 显示第一层的 32 个特征图 l0_features = features[0].numpy()[0] fig, ax = plt.subplots(4, 8, sharex=True, sharey=True, figsize=(16,8)) for i in range(0, 32): row, col = i//8, i%8 ax[row][col].imshow(l0_features[..., i]) plt.show() |
以上代码将打印特征图,如下所示:
这与以下输入图像相对应:
您可以看到它们被称为特征图,因为它们突出显示了输入图像中的某些特征。特征是通过一个小窗口(在本例中为 3x3 像素过滤器)识别的。输入图像有三个颜色通道。每个通道应用不同的过滤器,并且它们的结果组合成一个输出特征。
您可以类似地显示第二个卷积层输出的特征图,如下所示:
|
1 2 3 4 5 6 7 8 9 10 |
... # 显示第三层的 32 个特征图 l2_features = features[2].numpy()[0] fig, ax = plt.subplots(4, 8, sharex=True, sharey=True, figsize=(16,8)) for i in range(0, 32): row, col = i//8, i%8 ax[row][col].imshow(l2_features[..., i]) plt.show() |
这将显示以下内容: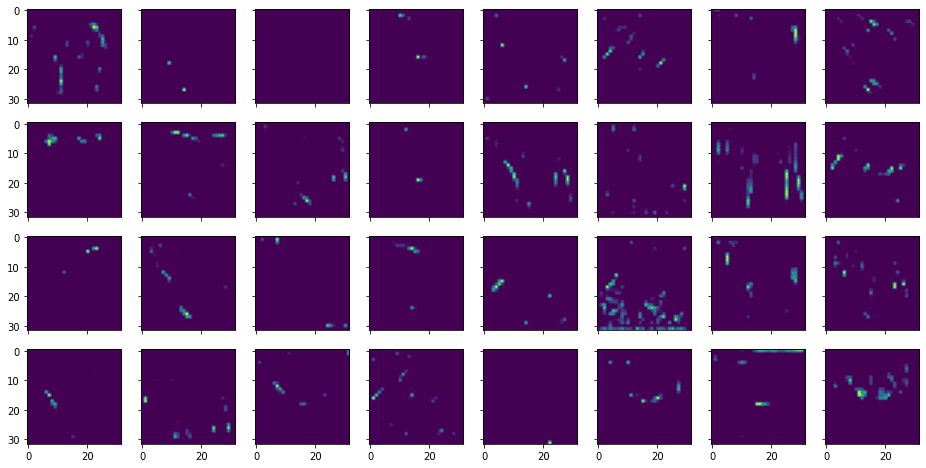
从上面可以看出,提取的特征更加抽象,识别度也较低。
卷积层的作用
卷积层最重要的超参数是滤波器大小。通常,它呈正方形,您可以将其视为一个**窗口**或**感受野**来查看输入图像。因此,图像分辨率越高,您就可以期望更大的滤波器。
另一方面,过大的滤波器会模糊细节特征,因为通过滤波器感受野的所有像素都将合并为输出特征图中的一个像素。因此,滤波器尺寸的选择需要在两者之间进行权衡。
堆叠两个卷积层(中间没有其他层)等同于使用一个更大滤波器的单个卷积层。但如今的典型设计是堆叠两个小滤波器层,而不是一个大滤波器层,因为这样需要训练的参数更少。
一个例外是使用 1x1 滤波器的卷积层。这通常作为网络的起始层。这种卷积层的目的是将输入通道组合成一个,而不是转换像素。从概念上讲,这可以将彩色图像转换为灰度,但通常您可以使用多种转换方式来创建比仅仅 RGB 更多的网络输入通道。
此外,请注意在上述网络中,您使用的是 `Conv2D` 用于 2D 滤波器。还有 `Conv3D` 层用于 3D 滤波器。区别在于您是为每个通道或特征图分别应用滤波器,还是将输入特征图堆叠成 3D 数组并应用单个滤波器进行整体转换。通常使用前者,因为将特征图的堆叠顺序视为没有特定顺序更为合理。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
文章
教程
总结
在这篇文章中,您已经了解了如何可视化卷积神经网络的特征图以及它如何提取特征图。
具体来说,你学到了:
- 典型卷积神经网络的结构
- 滤波器大小对卷积层的影响是什么?
- 在网络中堆叠卷积层有什么作用?



暂无评论。