如何优化单变量函数?
单变量函数优化涉及寻找导致目标函数获得最佳输出的函数的输入。
在机器学习中,当使用单个参数拟合模型或调整具有单个超参数的模型时,这是一种常见的操作。
需要一种有效的算法来解决这类优化问题,该算法能够在最少的函数评估次数内找到最佳解决方案,考虑到目标函数的每次评估都可能计算成本很高,例如在数据集上拟合和评估模型。
这排除了昂贵的网格搜索和随机搜索算法,而青睐 Brent 方法等高效算法。
在本教程中,您将了解如何在 Python 中执行单变量函数优化。
完成本教程后,您将了解:
- 单变量函数优化涉及为接受单个连续参数的目标函数找到最佳输入。
- 如何对无约束的凸函数执行单变量函数优化。
- 如何对无约束的非凸函数执行单变量函数优化。
开始您的项目,阅读我的新书《机器学习优化》,其中包括分步教程和所有示例的Python 源代码文件。
让我们开始吧。
Python中的单变量函数优化
照片作者:Robert Haandrikman,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 单变量函数优化
- 凸单变量函数优化
- 非凸单变量函数优化
单变量函数优化
我们可能需要找到一个接受单个参数的函数的最佳值。
在机器学习中,这可能发生在许多情况下,例如:
- 查找模型系数以拟合训练数据集。
- 查找单个超参数的值,该值可实现最佳模型性能。
这称为单变量函数优化。
我们可能对函数的最小输出或最大输出感兴趣,尽管这可以简化为最小化,因为可以通过给函数的所有输出加上负号来将最大化函数转换为最小化函数。
函数输入可能有限制,也可能没有,这称为无约束或有约束优化;我们假设输入的微小变化对应于输出的微小变化,即它是平滑的。
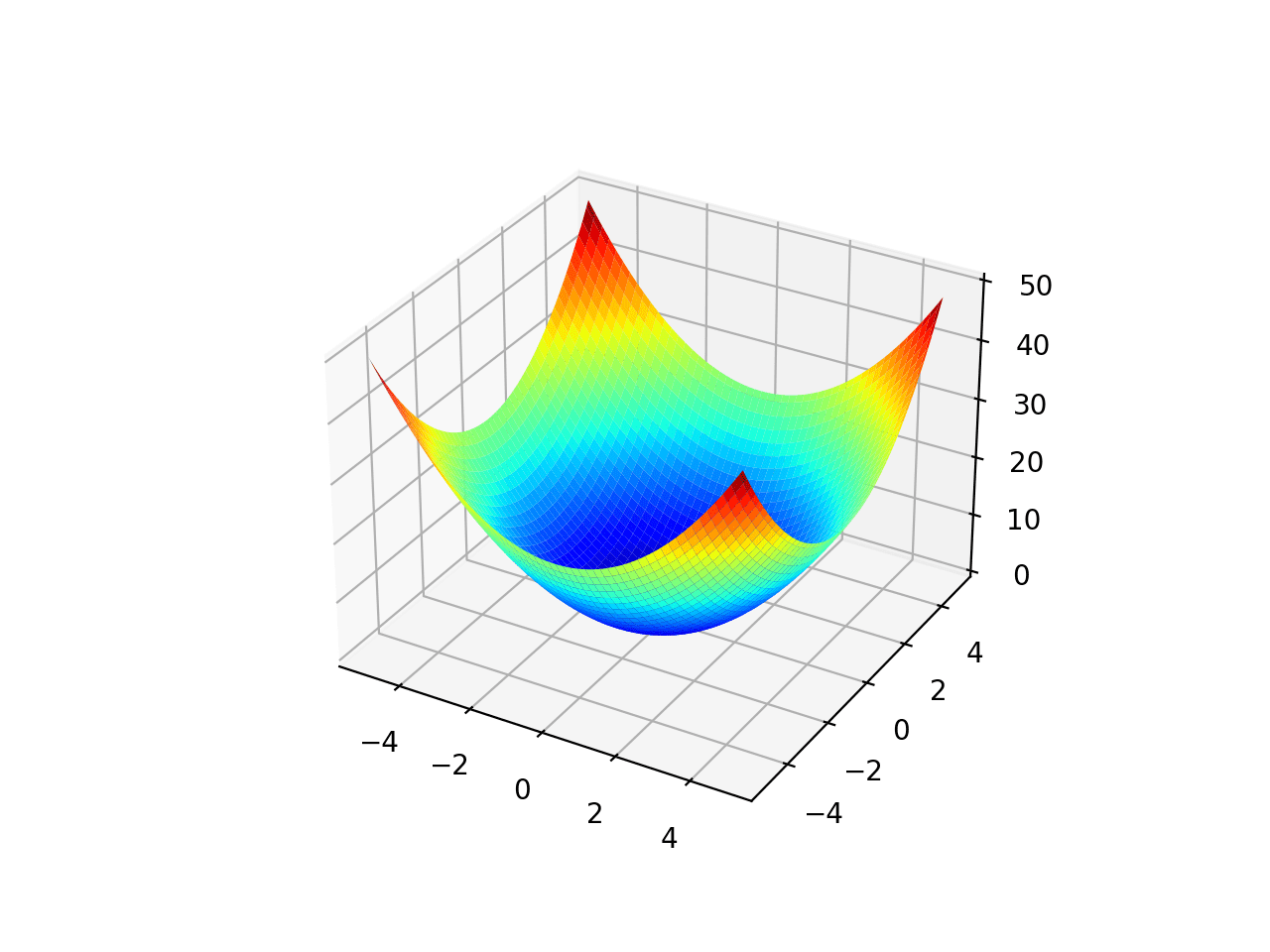
函数可能有一个或多个最优值,尽管我们希望它有一个最优值,并且函数的形状看起来像一个大盆地。如果是这样,我们知道我们可以通过一个点采样函数并找到通往函数最小值的路径。技术上,这被称为凸函数(对于最大化是凹函数),而那些不具有这种盆地形状的函数被称为非凸函数。
- 凸目标函数:存在一个最优值,并且目标函数的形状导向该最优值。
尽管如此,目标函数足够复杂,以至于我们不知道其导数,这意味着我们无法仅通过微积分来解析计算函数梯度为零时的最小值或最大值。这被称为非可微函数。
虽然我们可以使用候选值对函数进行采样,但我们不知道能带来最佳结果的输入。这可能是因为评估候选解决方案的成本很高,原因有很多。
因此,我们需要一个算法来有效地对函数的输入值进行采样。
解决单变量函数优化问题的一种方法是使用Brent 方法。
Brent 方法是一种优化算法,它结合了二分算法(Dekker 方法)和逆二次插值。它可用于约束和无约束的单变量函数优化。
Brent-Dekker 方法是二分法的一种扩展。它是一种求根算法,结合了割线法和逆二次插值的元素。它具有可靠且快速的收敛特性,是许多流行数值优化包中单变量优化算法的首选。
— 第 49-51 页,Algorithms for Optimization,2019。
二分算法使用输入值的区间(下限和上限)并分割输入域,对其进行二分以定位最优值在域中的位置,这很像二元搜索。Dekker 方法是实现这一目标的一种高效方法,适用于连续域。
Dekker 方法在非凸问题上会卡住。Brent 方法修改了 Dekker 方法以避免卡住,并近似目标函数的二阶导数(称为割线法),以加速搜索。
因此,鉴于其效率,Brent 方法在单变量函数优化方面通常优于大多数其他单变量函数优化算法。
Python 中可以通过 SciPy 的 minimize_scalar() 函数来使用 Brent 方法,该函数接受要最小化的函数名称。如果您的目标函数受限于某个范围,可以通过“bounds”参数指定。
它返回一个 OptimizeResult 对象,该对象是一个包含解决方案的字典。重要的是,“x”键总结了最优值的输入,“fun”键总结了最优值对应的函数输出,“nfev”总结了为定位最优值而执行的目标函数评估次数。
|
1 2 3 |
... # 最小化函数 result = minimize_scalar(objective, method='brent') |
现在我们知道了如何在 Python 中执行单变量函数优化,让我们看一些例子。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
凸单变量函数优化
在本节中,我们将探讨如何解决凸单变量函数优化问题。
首先,我们可以定义一个实现我们函数的函数。
在这种情况下,我们将使用 x^2 函数的简单偏移版本,即简单的抛物线(U 形)函数。这是一个最小化目标函数,其最优值为 -5.0。
|
1 2 3 |
# 目标函数 def objective(x): return (5.0 + x)**2.0 |
我们可以绘制该函数的粗略网格,输入值从 -10 到 10,以了解目标函数的形状。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 绘制凸目标函数 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return (5.0 + x)**2.0 # 定义范围 r_min, r_max = -10.0, 10.0 # 准备输入 inputs = arange(r_min, r_max, 0.1) # 计算目标值 targets = [objective(x) for x in inputs] # 绘制输入与目标 pyplot.plot(inputs, targets, '--') pyplot.show() |
运行示例,使用我们的目标函数评估指定范围内的输入值,并创建函数输入到函数输出的图。
我们可以看到函数的 U 形,并且目标值为 -5.0。
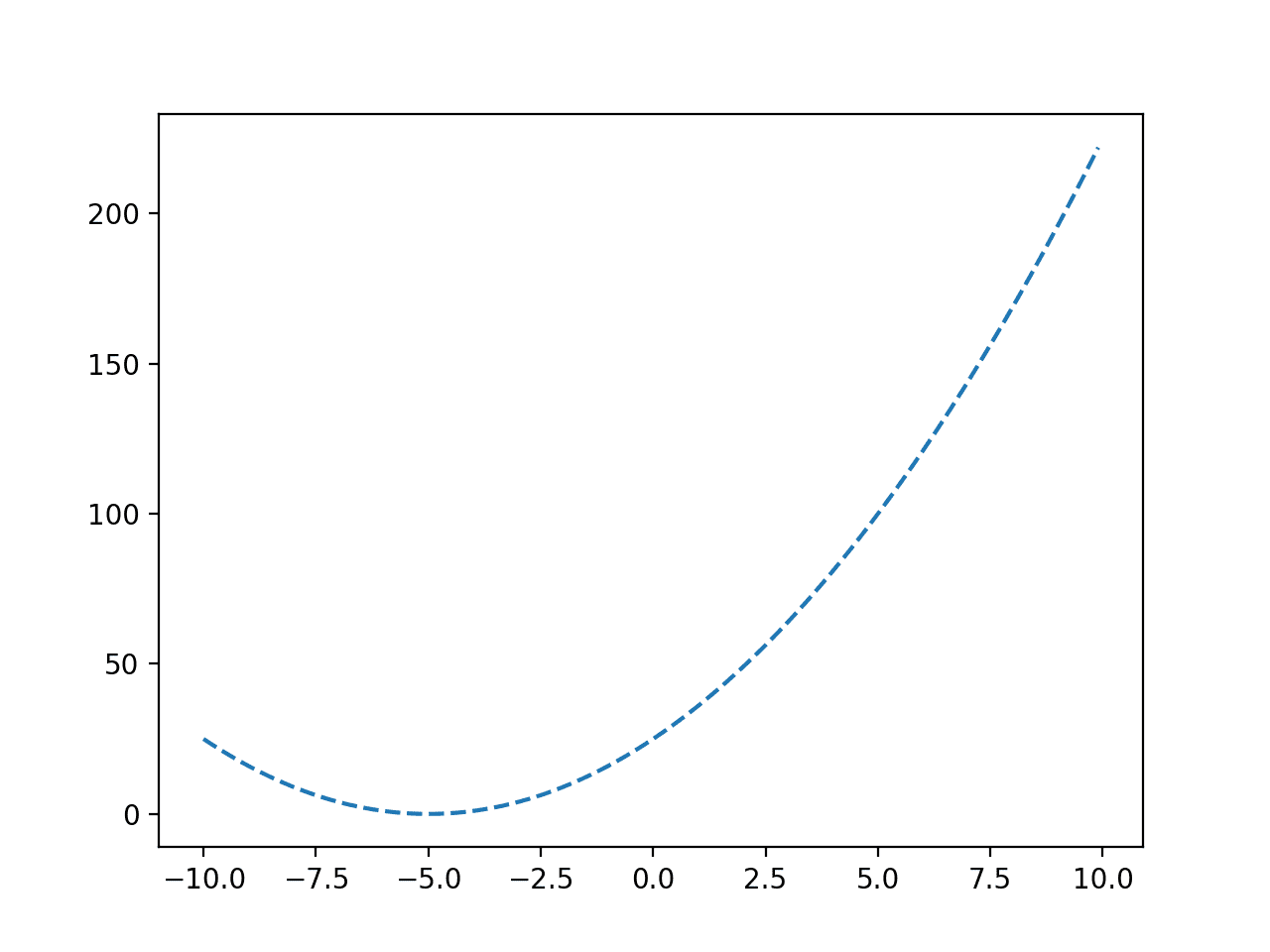
凸目标函数的线图
注意:在实际的优化问题中,我们无法如此轻松地进行如此多次函数评估。这个简单的函数用于演示目的,以便我们学习如何使用优化算法。
接下来,我们可以使用优化算法来查找最优值。
|
1 2 3 |
... # 最小化函数 result = minimize_scalar(objective, method='brent') |
优化后,我们可以总结结果,包括最优值的输入和评估,以及定位最优值所需的函数评估次数。
|
1 2 3 4 5 6 |
... # 总结结果 opt_x, opt_y = result['x'], result['fun'] print('最优输入 x: %.6f' % opt_x) print('最优输出 f(x): %.6f' % opt_y) print('总评估次数 n: %d' % result['nfev']) |
最后,我们可以再次绘制函数并标记最优值,以确认它已在该函数预期的位置找到。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
... # 定义范围 r_min, r_max = -10.0, 10.0 # 准备输入 inputs = arange(r_min, r_max, 0.1) # 计算目标值 targets = [objective(x) for x in inputs] # 绘制输入与目标 pyplot.plot(inputs, targets, '--') # 绘制最优值 pyplot.plot([opt_x], [opt_y], 's', color='r') # 显示绘图 pyplot.show() |
优化无约束凸单变量函数的完整示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
# 优化凸目标函数 from numpy import arange from scipy.optimize import minimize_scalar from matplotlib import pyplot # 目标函数 def objective(x): return (5.0 + x)**2.0 # 最小化函数 result = minimize_scalar(objective, method='brent') # 总结结果 opt_x, opt_y = result['x'], result['fun'] print('最优输入 x: %.6f' % opt_x) print('最优输出 f(x): %.6f' % opt_y) print('总评估次数 n: %d' % result['nfev']) # 定义范围 r_min, r_max = -10.0, 10.0 # 准备输入 inputs = arange(r_min, r_max, 0.1) # 计算目标值 targets = [objective(x) for x in inputs] # 绘制输入与目标 pyplot.plot(inputs, targets, '--') # 绘制最优值 pyplot.plot([opt_x], [opt_y], 's', color='r') # 显示绘图 pyplot.show() |
运行示例首先解决优化问题并报告结果。
注意:由于算法的随机性、评估过程或数值精度的差异,您的结果可能有所不同。请考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到最优值是在 10 次目标函数评估后找到的,输入为 -5.0,目标函数值为 0.0。
|
1 2 3 |
最优输入 x: -5.000000 最优输出 f(x): 0.000000 总评估次数 n: 10 |
再次创建函数的图,这次标记了最优值,为一个红色方块。
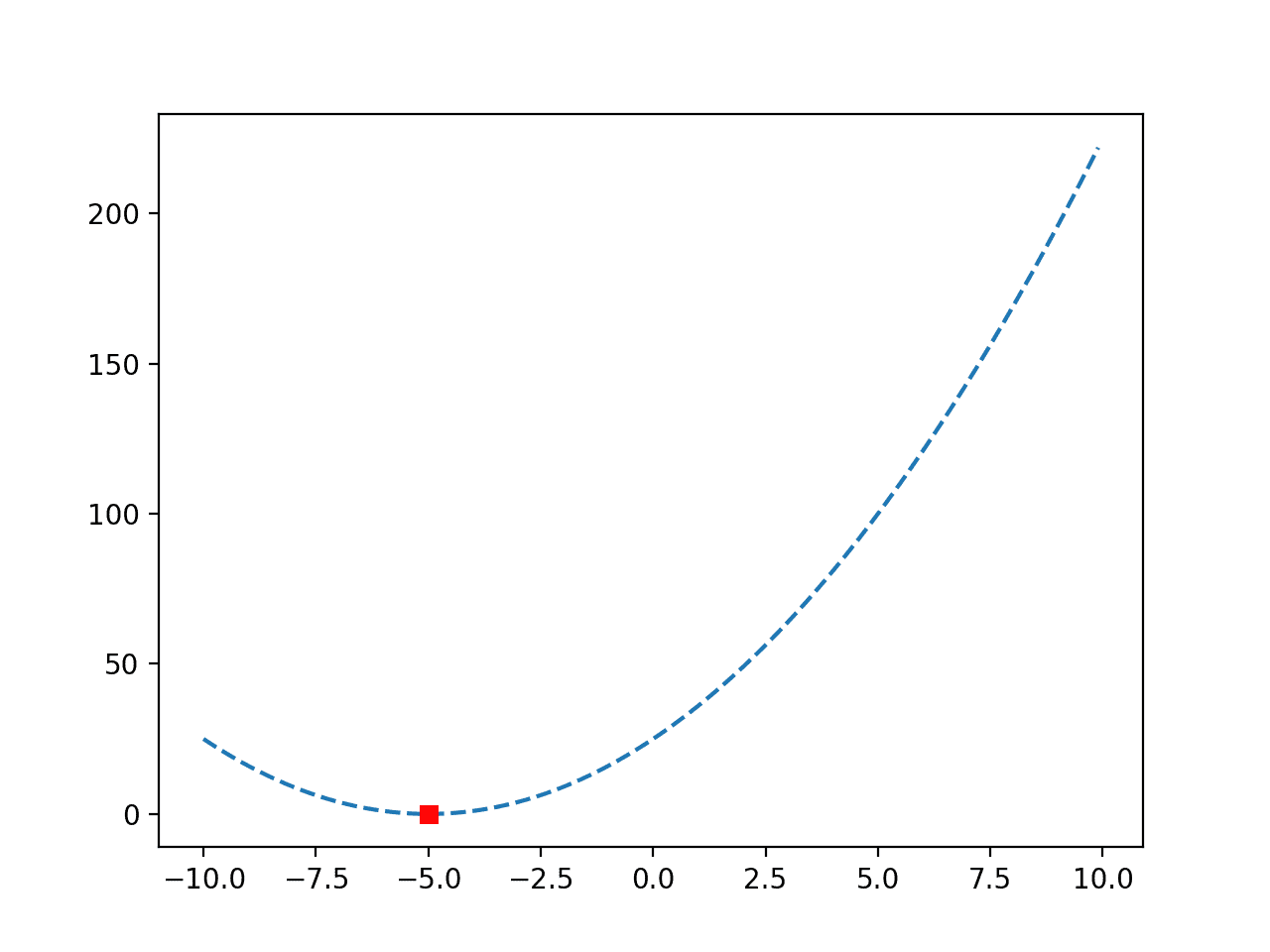
带最优值标记的凸目标函数线图
非凸单变量函数优化
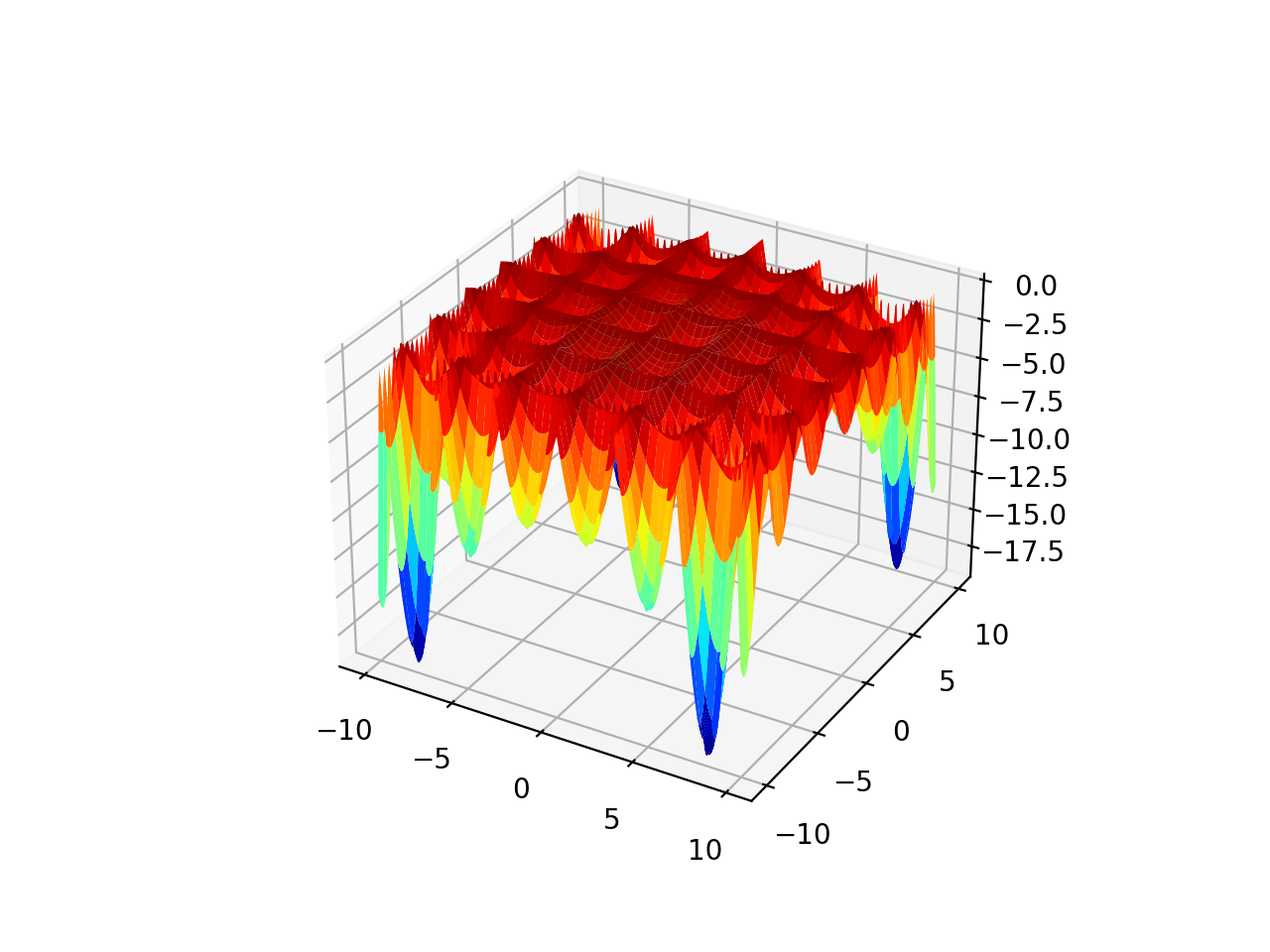
凸函数是指不呈现盆地形状的函数,这意味着它可能有一个以上的山丘或山谷。
这会使定位全局最优值更具挑战性,因为多个山丘和山谷可能导致搜索卡住,从而报告一个错误的局部最优值。
我们可以如下定义一个非凸单变量函数。
|
1 2 3 |
# 目标函数 def objective(x): return (x - 2.0) * x * (x + 2.0)**2.0 |
我们可以对该函数进行采样并创建输入值到目标值的线图。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 绘制非凸单变量函数 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return (x - 2.0) * x * (x + 2.0)**2.0 # 定义范围 r_min, r_max = -3.0, 2.5 # 准备输入 inputs = arange(r_min, r_max, 0.1) # 计算目标值 targets = [objective(x) for x in inputs] # 绘制输入与目标 pyplot.plot(inputs, targets, '--') pyplot.show() |
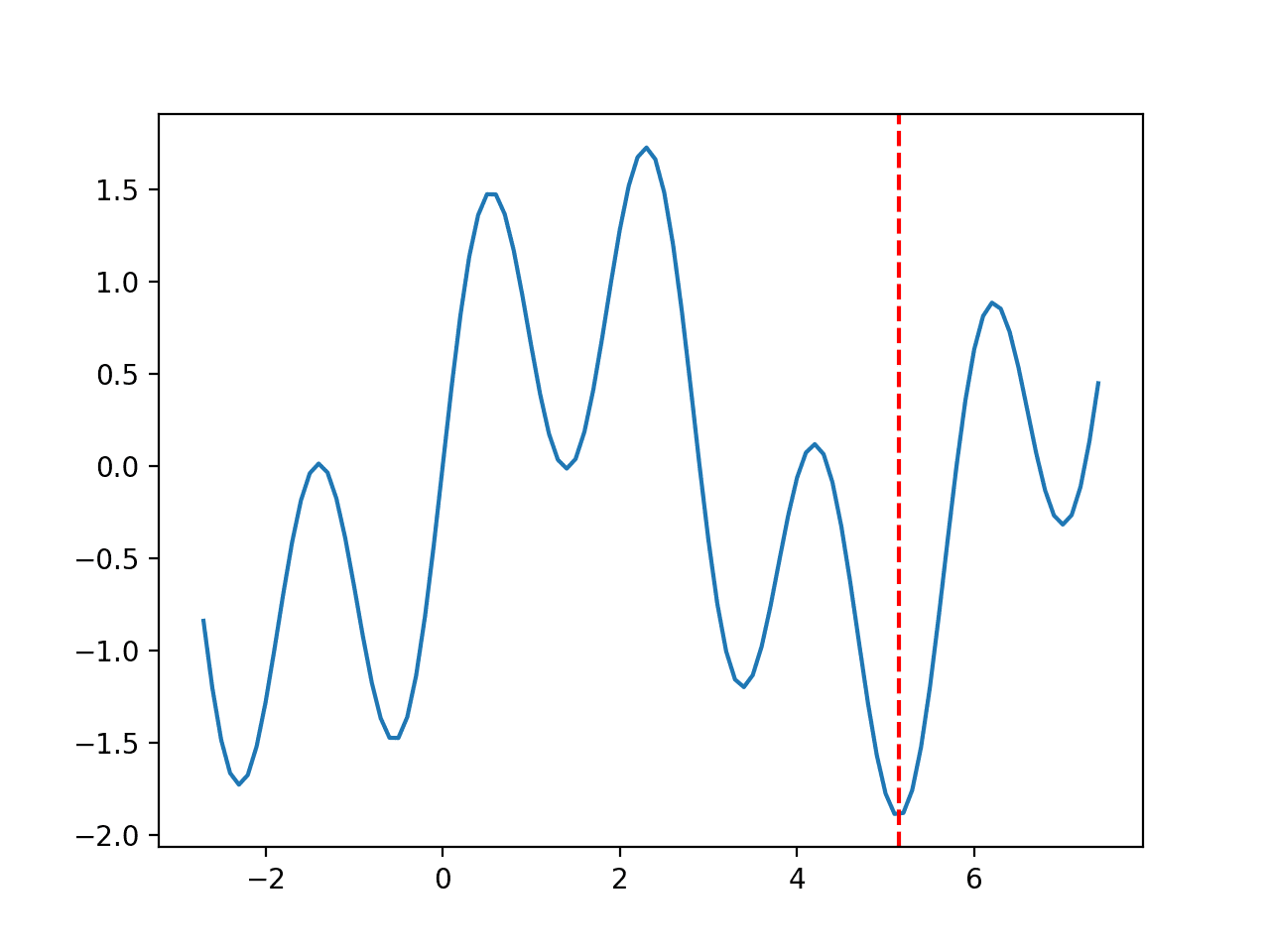
运行示例,使用我们的目标函数评估指定范围内的输入值,并创建函数输入到函数输出的图。
我们可以看到一个函数,其虚假最优值在 -2.0 附近,全局最优值在 1.2 附近。
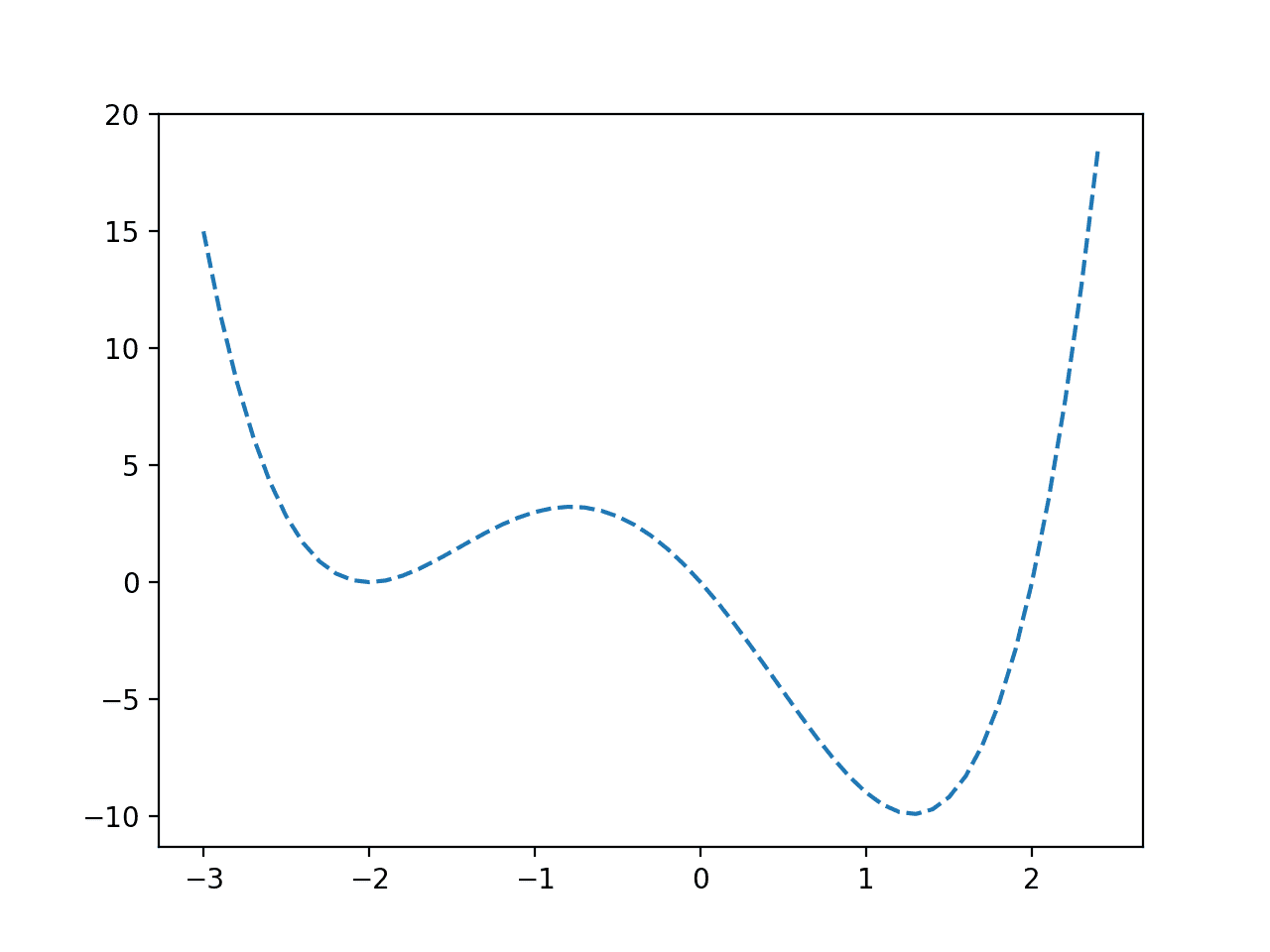
非凸目标函数的线图
注意:在实际的优化问题中,我们无法如此轻松地进行如此多次函数评估。这个简单的函数用于演示目的,以便我们学习如何使用优化算法。
接下来,我们可以使用优化算法来查找最优值。
和以前一样,我们可以调用 minimize_scalar() 函数来优化该函数,然后总结结果并将最优值绘制在线图上。
优化无约束非凸单变量函数的完整示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
# 优化非凸目标函数 from numpy import arange from scipy.optimize import minimize_scalar from matplotlib import pyplot # 目标函数 def objective(x): return (x - 2.0) * x * (x + 2.0)**2.0 # 最小化函数 result = minimize_scalar(objective, method='brent') # 总结结果 opt_x, opt_y = result['x'], result['fun'] print('最优输入 x: %.6f' % opt_x) print('最优输出 f(x): %.6f' % opt_y) print('总评估次数 n: %d' % result['nfev']) # 定义范围 r_min, r_max = -3.0, 2.5 # 准备输入 inputs = arange(r_min, r_max, 0.1) # 计算目标值 targets = [objective(x) for x in inputs] # 绘制输入与目标 pyplot.plot(inputs, targets, '--') # 绘制最优值 pyplot.plot([opt_x], [opt_y], 's', color='r') # 显示绘图 pyplot.show() |
运行示例首先解决优化问题并报告结果。
想开始学习集成学习吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
在这种情况下,我们可以看到最优值是在 15 次目标函数评估后找到的,输入约为 1.28,目标函数值约为 -9.91。
|
1 2 3 |
最优输入 x: 1.280776 最优输出 f(x): -9.914950 总评估次数 n: 15 |
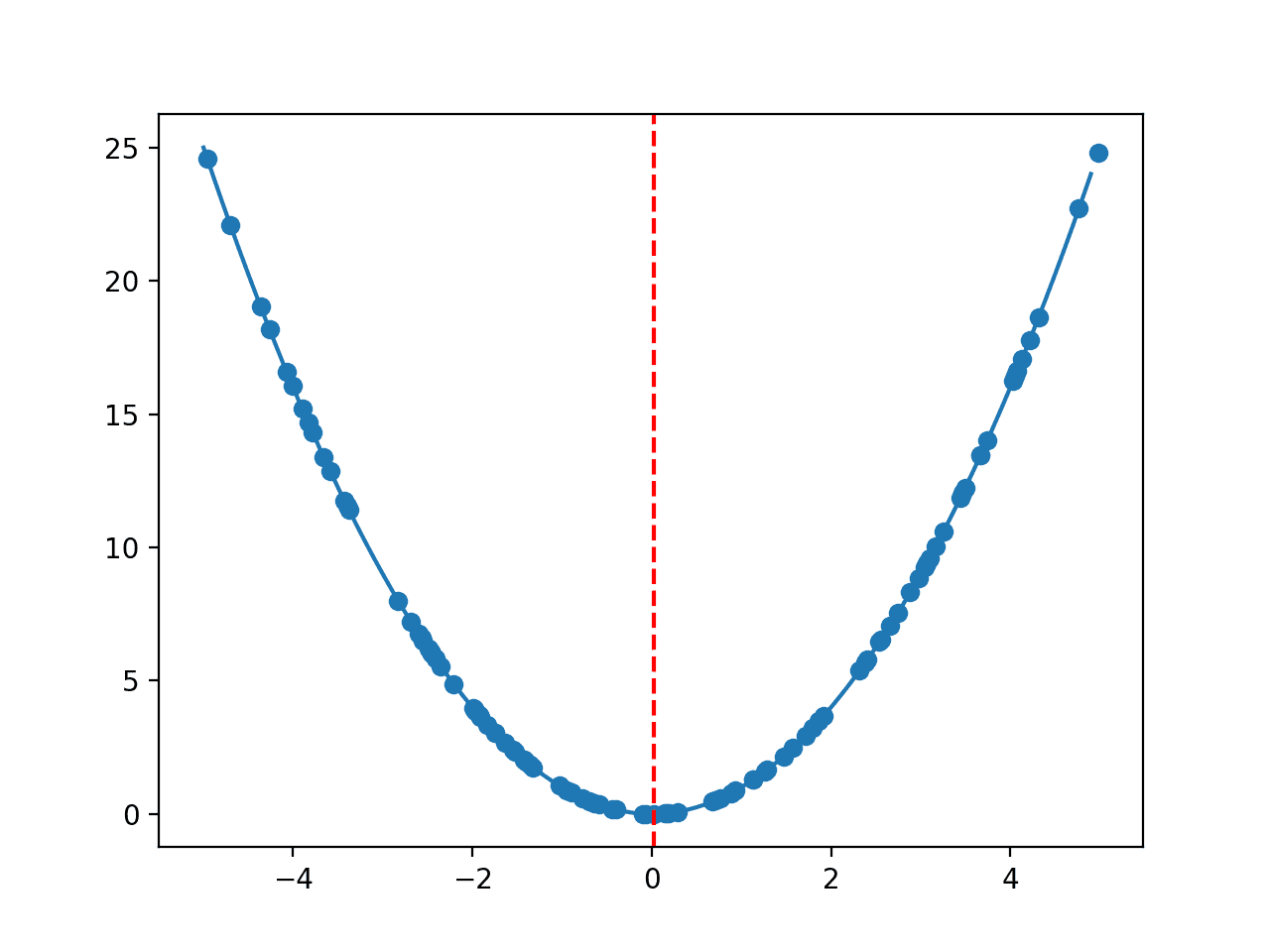
再次创建函数的图,这次标记了最优值,为一个红色方块。
我们可以看到优化算法没有被虚假最优值欺骗,并且成功找到了全局最优值。
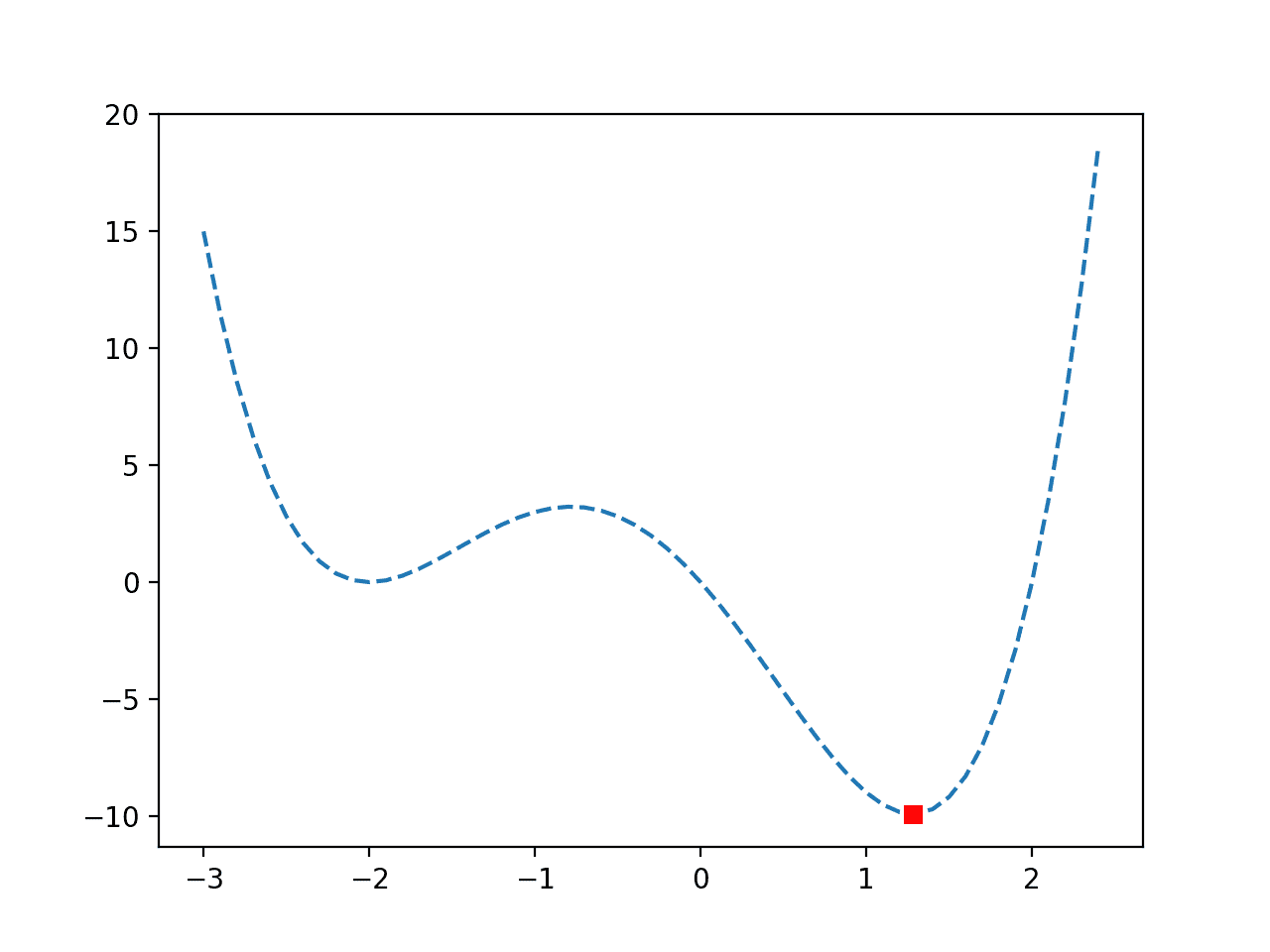
带最优值标记的非凸目标函数线图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 优化算法, 2019.
API
文章
总结
在本教程中,您学习了如何在 Python 中执行单变量函数优化。
具体来说,你学到了:
- 单变量函数优化涉及为接受单个连续参数的目标函数找到最佳输入。
- 如何对无约束的凸函数执行单变量函数优化。
- 如何对无约束的非凸函数执行单变量函数优化。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



你为什么不写一本关于机器学习优化的正式书籍?我拥有你所有的机器学习书籍,但优化部分缺失了。
很好的建议。我正在进行中。
“凸函数是指不呈现盆地形状的函数”。你的意思是“非凸函数是指不呈现盆地形状的函数”吗?
是的,你的优化书籍会很棒!谢谢你的作品。
这是函数绘图时的形状。
另外,更多关于凸函数的内容
https://en.wikipedia.org/wiki/Convex_function
我同意优化书籍的想法!🙂
谢谢。