如何使用统计显著性检验来解释机器学习结果

作者 Jason Brownlee 于 2019年8月8日发表于统计学 37

在比较两种不同的机器学习算法或比较同一算法的不同配置时，收集一组结果是一个好习惯。

重复进行每次实验运行30次或更多次，可以得到一组结果，从中可以计算出预期的平均性能，这是因为大多数机器学习算法都具有随机性。

如果两种算法或配置的预期平均性能不同，你怎么知道这种差异是否显著，以及显著到什么程度？

统计显著性检验是帮助解释机器学习实验结果的重要工具。此外，这些工具的发现可以帮助你更好地、更自信地展示你的实验结果，并为你的预测建模问题选择合适的算法和配置。

在本教程中，你将学习如何使用Python中的统计显著性检验来研究和解释机器学习实验结果。

完成本教程后，您将了解：

如何应用正态性检验来确认你的数据是否（或不是）正态分布。
如何应用参数统计显著性检验来处理正态分布的结果。
如何应用非参数统计显著性检验来处理更复杂的结果分布。

通过我新书《机器学习统计学》快速启动你的项目，书中包含分步教程和所有示例的Python源代码文件。

让我们开始吧。

更新于2018年5月：更新了与“拒绝”和“未能拒绝”H0相关的语言。

How to Use Statistical Significance Tests to Interpret Machine Learning Results

如何使用统计显著性检验来解释机器学习结果
照片由oatsy40拍摄，部分权利保留。

教程概述

本教程分为6个部分。它们是：

生成样本数据
描述性统计
正态性检验
比较高斯结果的均值
比较方差不同的高斯结果的均值
比较非高斯结果的均值

本教程假定您使用Python 2或3以及带有NumPy、Pandas和Matplotlib的SciPy环境。

需要机器学习统计学方面的帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

生成样本数据

情况是您获得了两种算法或同一算法的两种不同配置的实验结果。

每种算法都在测试数据集上进行了多次试验，并收集了技能得分。我们剩下两组技能得分。

我们可以通过生成两个具有略微不同均值的正态随机数总体来模拟这种情况。

以下代码生成了第一种算法的结果。总共1000个结果存储在一个名为*results1.csv*的文件中。结果是从均值为50、标准差为10的正态分布中抽取的。

from numpy.random import seed
from numpy.random import normal
from numpy import savetxt
# define underlying distribution of results
mean = 50
stev = 10
# generate samples from ideal distribution
seed(1)
results = normal(mean, stev, 1000)
# save to ASCII file
savetxt('results1.csv', results)

from numpy.random import seed

from numpy.random import normal

from numpy import savetxt

# 定义结果的底层分布

mean = 50

stev = 10

# 从理想分布生成样本

seed(1)

results = normal(mean, stev, 1000)

# 保存到ASCII文件

savetxt('results1.csv', results)

下面是*results1.csv*中前5行数据的片段。

6.624345363663240960e+01
4.388243586349924641e+01
4.471828247736544171e+01
3.927031377843829318e+01
5.865407629324678851e+01
...

6.624345363663240960e+01

4.388243586349924641e+01

4.471828247736544171e+01

3.927031377843829318e+01

5.865407629324678851e+01

...

我们现在可以生成第二种算法的结果。我们将使用相同的方法，并从略有不同的高斯分布（均值为60，标准差相同）中抽取结果。结果将被写入*results2.csv*。

from numpy.random import seed
from numpy.random import normal
from numpy import savetxt
# define underlying distribution of results
mean = 60
stev = 10
# generate samples from ideal distribution
seed(1)
results = normal(mean, stev, 1000)
# save to ASCII file
savetxt('results2.csv', results)

from numpy.random import seed

from numpy.random import normal

from numpy import savetxt

# 定义结果的底层分布

mean = 60

stev = 10

# 从理想分布生成样本

seed(1)

results = normal(mean, stev, 1000)

# 保存到ASCII文件

savetxt('results2.csv', results)

下面是*results2.csv*中前5行数据的样本。

7.624345363663240960e+01
5.388243586349924641e+01
5.471828247736544171e+01
4.927031377843829318e+01
6.865407629324678851e+01
...

7.624345363663240960e+01

5.388243586349924641e+01

5.471828247736544171e+01

4.927031377843829318e+01

6.865407629324678851e+01

...

接下来，我们将假设我们不知道任何一组结果的底层分布。

我选择每个实验1000个结果的总体是任意的。使用30或100个结果的总体来实现足够好的估计（例如，低标准误差）会更现实。

如果你的结果不是高斯分布，也不用担心；我们将看看这些方法在非高斯数据上如何失效以及用什么替代方法。

描述性统计

收集结果后的第一步是查看一些摘要统计数据，并了解更多关于数据分布的信息。

这包括查看摘要统计和数据图。

下面是查看两组结果摘要统计的完整代码列表。

from pandas import DataFrame
from pandas import read_csv
from matplotlib import pyplot
# load results file
results = DataFrame()
results['A'] = read_csv('results1.csv', header=None).values[:, 0]
results['B'] = read_csv('results2.csv', header=None).values[:, 0]
# descriptive stats
print(results.describe())
# box and whisker plot
results.boxplot()
pyplot.show()
# histogram
results.hist()
pyplot.show()

from pandas import DataFrame

from pandas import read_csv

from matplotlib import pyplot

# 加载结果文件

results = DataFrame()

results['A'] = read_csv('results1.csv', header=None).values[:, 0]

results['B'] = read_csv('results2.csv', header=None).values[:, 0]

# 描述性统计

print(results.describe())

# 箱线图

results.boxplot()

pyplot.show()

# 直方图

results.hist()

pyplot.show()

示例加载了两组结果，并首先打印了摘要统计信息。为了简洁起见，*results1.csv*中的数据称为“A”，*results2.csv*中的数据称为“B”。

我们将假设这些数据代表测试集上的错误分数，并且最小化分数是目标。

我们可以看到，平均而言，A（50.388125）比B（60.388125）要好。我们还可以从其中位数（第50个百分位数）看到相同的情况。从标准差来看，我们还可以看到两个分布似乎具有相似（相同）的散布。

                 A            B
count  1000.000000  1000.000000
mean     50.388125    60.388125
std       9.814950     9.814950
min      19.462356    29.462356
25%      43.998396    53.998396
50%      50.412926    60.412926
75%      57.039989    67.039989
max      89.586027    99.586027

A B

count 1000.000000 1000.000000

mean 50.388125 60.388125

std 9.814950 9.814950

min 19.462356 29.462356

25% 43.998396 53.998396

50% 50.412926 60.412926

75% 57.039989 67.039989

max 89.586027 99.586027

接下来，创建了一个比较两组结果的箱线图。箱体捕获了数据的前50%，异常值显示为点，绿线显示为中位数。我们可以看到，这两个分布的数据确实具有相似的散布，并且似乎围绕中位数对称。

A的结果看起来比B好。

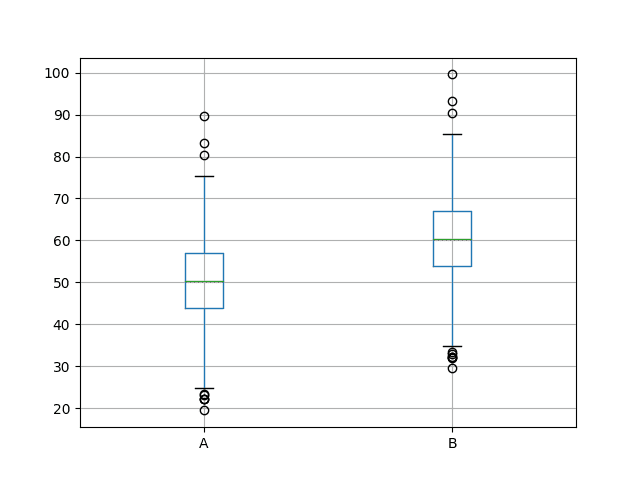
Box and Whisker Plots of Both Sets of Results

两组结果的箱线图

最后，绘制了两组结果的直方图。

这些图强烈表明两组结果都是从高斯分布中抽取的。

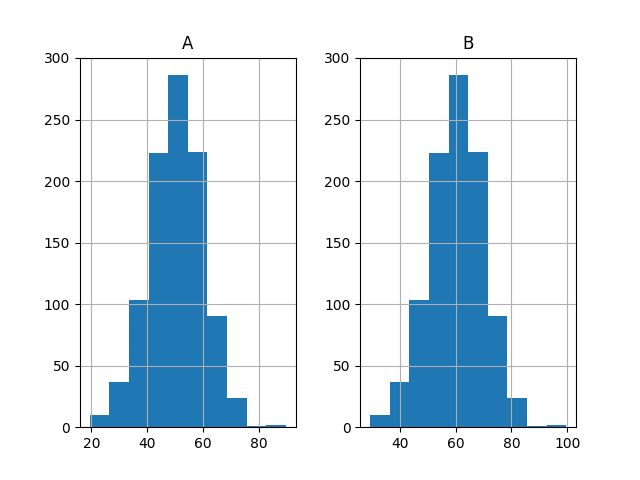
两组结果的直方图

正态性检验

从高斯分布中抽样的数据更容易处理，因为有许多专门为此情况设计的工具和技术。

我们可以使用统计检验来确认从两个分布中抽取的样本是高斯分布（也称为正态分布）。

在SciPy中，这是normaltest()函数。

根据文档，该测试描述为：

检验样本是否与正态分布不同。

该检验的零假设（H0），或默认期望是该统计量描述了一个正态分布。

如果p值大于0.05，我们将无法拒绝此假设。如果p值小于等于0.05，我们将拒绝此假设。在这种情况下，我们将有95%的信心认为该分布不是正态的。

以下代码加载*results1.csv*并确定数据是否可能为高斯分布。

from pandas import read_csv
from scipy.stats import normaltest
from matplotlib import pyplot
result1 = read_csv('results1.csv', header=None)
value, p = normaltest(result1.values[:,0])
print(value, p)
if p >= 0.05:
	print('It is likely that result1 is normal')
else:
	print('It is unlikely that result1 is normal')

from pandas import read_csv

from scipy.stats import normaltest

from matplotlib import pyplot

result1 = read_csv('results1.csv', header=None)

value, p = normaltest(result1.values[:,0])

print(value, p)

if p >= 0.05:

print('result1很可能是正态的')

else:

print('result1很可能不是正态的')

运行示例后，首先打印计算出的统计量以及计算该统计量的p值，它是否来自高斯分布。

我们可以看到，*results1.csv*很可能是高斯分布。

2.99013078116 0.224233941463
It is likely that result1 is normal

1 2	2.99013078116 0.224233941463 result1很可能是正态的

我们可以对*results2.csv*的数据重复进行相同的测试。

完整的代码列表如下。

from pandas import read_csv
from scipy.stats import normaltest
from matplotlib import pyplot
result2 = read_csv('results2.csv', header=None)
value, p = normaltest(result2.values[:,0])
print(value, p)
if p >= 0.05:
	print('It is likely that result2 is normal')
else:
	print('It is unlikely that result2 is normal')

from pandas import read_csv

from scipy.stats import normaltest

from matplotlib import pyplot

result2 = read_csv('results2.csv', header=None)

value, p = normaltest(result2.values[:,0])

print(value, p)

if p >= 0.05:

print('result2很可能是正态的')

else:

print('result2很可能不是正态的')

运行示例后，会得到相同的统计p值和结果。

两组结果都是高斯分布。

2.99013078116 0.224233941463
It is likely that result2 is normal

1 2	2.99013078116 0.224233941463 result2很可能是正态的

比较高斯结果的均值

两组结果都是高斯分布且具有相同的方差；这意味着我们可以使用Student t检验来查看两分布均值之间的差异是否具有统计学意义。

在SciPy中，我们可以使用ttest_ind()函数。

该检验描述为：

计算两个独立样本得分均值的T检验。

该检验的零假设（H0）或默认期望是两个样本来自同一总体。如果我们未能拒绝这个假设，这意味着均值之间没有显著差异。

如果我们得到的p值小于等于0.05，这意味着我们可以拒绝零假设，并且在95%的置信度下，均值存在显著差异。这意味着在100个相似的样本中，有95个样本的均值会存在显著差异，而有5个样本不会。

除了数据是高斯分布之外，此统计检验的一个重要假设是两个分布具有相同的方差。从上一步查看描述性统计信息中，我们知道情况确实如此。

完整的代码列表如下。

from pandas import read_csv
from scipy.stats import ttest_ind
from matplotlib import pyplot
# load results1
result1 = read_csv('results1.csv', header=None)
values1 = result1.values[:,0]
# load results2
result2 = read_csv('results2.csv', header=None)
values2 = result2.values[:,0]
# calculate the significance
value, pvalue = ttest_ind(values1, values2, equal_var=True)
print(value, pvalue)
if pvalue > 0.05:
	print('Samples are likely drawn from the same distributions (fail to reject H0)')
else:
	print('Samples are likely drawn from different distributions (reject H0)')

from pandas import read_csv

from scipy.stats import ttest_ind

from matplotlib import pyplot

# 加载results1

result1 = read_csv('results1.csv', header=None)

values1 = result1.values[:,0]

# 加载results2

result2 = read_csv('results2.csv', header=None)

values2 =result2.values[:,0]

# 计算显著性

value, pvalue = ttest_ind(values1, values2, equal_var=True)

print(value, pvalue)

if pvalue > 0.05:

print('样本很可能来自相同的分布（未能拒绝H0）')

else:

print('样本很可能来自不同的分布（拒绝H0）')

运行示例后，会打印出统计量和p值。我们可以看到p值远小于0.05。

事实上，它小到几乎可以肯定均值之间的差异具有统计学意义。

-22.7822655028 2.5159901708e-102
Samples are likely drawn from different distributions (reject H0)

1 2	-22.7822655028 2.5159901708e-102 样本很可能来自不同的分布（拒绝H0）

比较方差不同的高斯结果的均值

如果两组结果的均值相同，但方差不同，会怎样？

我们不能直接使用Student t检验。事实上，我们必须使用该检验的一个修改版本，称为Welch t检验。

在SciPy中，这是相同的ttest_ind()函数，但我们必须将“equal_var”参数设置为“False”，以表明方差不相等。

我们可以通过一个示例来演示这一点，在该示例中，我们生成了两组均值非常接近（50 vs 51）但标准差差异很大（1 vs 10）的结果。我们将生成100个样本。

from numpy.random import seed
from numpy.random import normal
from scipy.stats import ttest_ind
# generate results
seed(1)
n = 100
values1 = normal(50, 1, n)
values2 = normal(51, 10, n)
# calculate the significance
value, pvalue = ttest_ind(values1, values2, equal_var=False)
print(value, pvalue)
if pvalue > 0.05:
	print('Samples are likely drawn from the same distributions (fail to reject H0)')
else:
	print('Samples are likely drawn from different distributions (reject H0)')

from numpy.random import seed

from numpy.random import normal

from scipy.stats import ttest_ind

# 生成结果

seed(1)

n = 100

values1 = normal(50, 1, n)

values2 = normal(51, 10, n)

# 计算显著性

value, pvalue = ttest_ind(values1, values2, equal_var=False)

print(value, pvalue)

if pvalue > 0.05:

print('样本很可能来自相同的分布（未能拒绝H0）')

else:

print('样本很可能来自不同的分布（拒绝H0）')

运行示例后，会打印出检验统计量和p值。

我们可以看到，有很好的证据（接近99%）表明样本来自不同的分布，即均值存在显著差异。

-2.62233137406 0.0100871483783
Samples are likely drawn from different distributions (reject H0)

1 2	-2.62233137406 0.0100871483783 样本很可能来自不同的分布（拒绝H0）

分布越接近，区分它们所需的样本就越大。

我们可以通过计算每个结果的不同子样本的统计检验，并将p值与样本大小绘制出来来证明这一点。

我们期望p值随着样本量的增加而减小。我们还可以画一条95%的线（0.05），并显示样本量大到足以表明这两个总体存在显著差异的点。

from numpy.random import seed
from numpy.random import normal
from scipy.stats import ttest_ind
from matplotlib import pyplot
# generate results
seed(1)
n = 100
values1 = normal(50, 1, n)
values2 = normal(51, 10, n)
# calculate p-values for different subsets of results
pvalues = list()
for i in range(1, n+1):
	value, p = ttest_ind(values1[0:i], values2[0:i], equal_var=False)
	pvalues.append(p)
# plot p-values vs number of results in sample
pyplot.plot(pvalues)
# draw line at 95%, below which we reject H0
pyplot.plot([0.05 for x in range(len(pvalues))], color='red')
pyplot.show()

from numpy.random import seed

from numpy.random import normal

from scipy.stats import ttest_ind

from matplotlib import pyplot

# 生成结果

seed(1)

n = 100

values1 = normal(50, 1, n)

values2 = normal(51, 10, n)

# 计算不同结果子集的p值

pvalues = list()

for i in range(1, n+1):

value, p = ttest_ind(values1[0:i], values2[0:i], equal_var=False)

pvalues.append(p)

# 绘制p值与样本数量的关系图

pyplot.plot(pvalues)

# 绘制95%的阈值线，低于此线则拒绝H0

pyplot.plot([0.05 for x in range(len(pvalues))], color='red')

pyplot.show()

运行示例后，会生成一个p值与样本大小的折线图。

我们可以看到，对于这两组结果，样本量必须约为90，我们才有95%的信心认为均值存在显著差异（蓝色线与红色线相交处）。

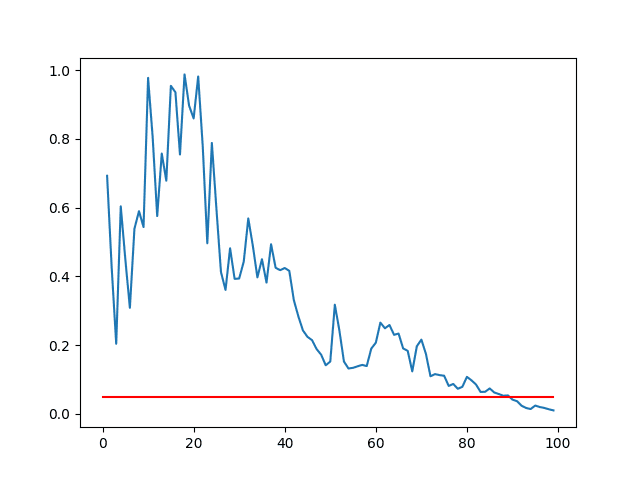
Line Plot of p-values for Datasets with a Differing Variance

p值与样本大小的折线图

比较非高斯结果的均值

如果我们的数据不是高斯分布，我们就不能使用Student t检验或Welch t检验。

我们可以用于非高斯数据的另一种统计显著性检验称为Kolmogorov-Smirnov检验。

在SciPy中，这被称为ks_2samp()函数。

在文档中，该检验描述为：

这是用于检验两个独立样本是否来自同一连续分布的零假设的双边检验。

此检验可用于高斯数据，但其统计功效较低，可能需要大样本。

我们可以通过一个示例来演示对两组非高斯分布结果的统计显著性计算。我们可以生成两组具有重叠均匀分布（50至60和55至65）的结果。这些结果集将分别具有约55和60的不同均值。

以下代码生成了两组100个结果，并使用Kolmogorov-Smirnov检验来证明总体均值之间的差异具有统计学意义。

from numpy.random import seed
from numpy.random import randint
from scipy.stats import ks_2samp
# generate results
seed(1)
n = 100
values1 = randint(50, 60, n)
values2 = randint(55, 65, n)
# calculate the significance
value, pvalue = ks_2samp(values1, values2)
print(value, pvalue)
if pvalue > 0.05:
	print('Samples are likely drawn from the same distributions (fail to reject H0)')
else:
	print('Samples are likely drawn from different distributions (reject H0)')

from numpy.random import seed

from numpy.random import randint

from scipy.stats import ks_2samp

# 生成结果

seed(1)

n = 100

values1 = randint(50, 60, n)

values2 = randint(55, 65, n)

# 计算显著性

value, pvalue = ks_2samp(values1, values2)

print(value, pvalue)

if pvalue > 0.05:

print('样本很可能来自相同的分布（未能拒绝H0）')

else:

print('样本很可能来自不同的分布（拒绝H0）')

运行示例后，会打印出统计量和p值。

p值非常小，表明总体之间存在差异几乎可以肯定是显著的。

0.47 2.16825856737e-10
Samples are likely drawn from different distributions (reject H0)

1 2	0.47 2.16825856737e-10 样本很可能来自不同的分布（拒绝H0）

进一步阅读

本节列出了一些文章和资源，供您深入研究应用机器学习的统计显著性检验。

总结

在本教程中，您了解了如何使用统计显著性检验来解释机器学习结果。

您可以使用这些检验来帮助您自信地选择一种机器学习算法而不是另一种，或者为同一种算法选择一组配置参数而不是另一组。

您学到了

如何使用正态性检验来检查您的实验结果是否为高斯分布。
如何使用统计检验来检查对于具有相同和不同方差的高斯数据，平均结果之间的差异是否具有统计学意义。
如何使用统计检验来检查对于非高斯数据，平均结果之间的差异是否具有统计学意义。

您对这篇文章或统计显著性检验有任何疑问吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

估计随机机器学习算法的实验重复次数

使用LSTM网络进行时间序列预测的权重正则化