LSTM 网络中的权重正则化用于时间序列预测

作者： Jason Brownlee 于 2020年8月28日发布在时间序列深度学习 65

长短期记忆（LSTM）模型是一种循环神经网络，能够学习观测序列。

这使得它们非常适合时间序列预测。

LSTM 的一个问题是它们很容易过拟合训练数据，从而降低其预测能力。

加权正则化是一种将约束（例如 L1 或 L2）施加于 LSTM 节点内权重的技术。这可以减少过拟合并提高模型性能。

在本教程中，您将了解如何将加权正则化与 LSTM 网络结合使用，并设计实验来测试其在时间序列预测中的有效性。

完成本教程后，您将了解：

如何设计一个健壮的测试框架来评估 LSTM 网络在时间序列预测中的表现。
如何设计、执行和解释使用偏置加权正则化与 LSTM 的结果。
如何设计、执行和解释使用输入和循环加权正则化与 LSTM 的结果。

通过我的新书《时间序列预测深度学习》启动您的项目，其中包含分步教程和所有示例的Python源代码文件。

让我们开始吧。

2019 年 4 月更新：更新了数据集链接。

How to Use Weight Regularization with LSTM Networks for Time Series Forecasting

如何将加权正则化与 LSTM 网络用于时间序列预测
摄影：Julian Fong，保留部分权利。

教程概述

本教程分为6个部分。它们是：

洗发水销售数据集
实验测试框架
偏置加权正则化
输入加权正则化
循环加权正则化
结果回顾

环境

本教程假定您已安装 Python SciPy 环境。您可以使用 Python 2 或 3。

本教程假定您已安装 Keras v2.0 或更高版本，并使用 TensorFlow 或 Theano 后端。

本教程还假定您已安装 scikit-learn、Pandas、NumPy 和 Matplotlib。

如果您需要帮助设置 Python 环境，请参阅此帖子

如何使用 Anaconda 设置用于机器学习和深度学习的 Python 环境

接下来，让我们看看一个标准的时间序列预测问题，我们可以将其作为本次实验的背景。

时间序列深度学习需要帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

洗发水销售数据集

此数据集描述了 3 年期间洗发水月销量。

单位是销售计数，共有 36 个观测值。原始数据集归功于 Makridakis、Wheelwright 和 Hyndman (1998)。

下载数据集.

以下示例加载并创建加载数据集的图表。

# load and plot dataset
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
# load dataset
def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# summarize first few rows
print(series.head())
# line plot
series.plot()
pyplot.show()

# 加载并绘制数据集

from pandas import read_csv

from pandas import datetime

from matplotlib import pyplot

# 加载数据集

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 总结前几行

print(series.head())

# 线图

series.plot()

pyplot.show()

运行该示例将数据集作为 Pandas Series 加载并打印前 5 行。

Month
1901-01-01 266.0
1901-02-01 145.9
1901-03-01 183.1
1901-04-01 119.3
1901-05-01 180.3
Name: Sales, dtype: float64

月份

1901-01-01 266.0

1901-02-01 145.9

1901-03-01 183.1

1901-04-01 119.3

1901-05-01 180.3

名称：销售额，数据类型：float64

然后创建该系列的线图，显示出明显的上升趋势。

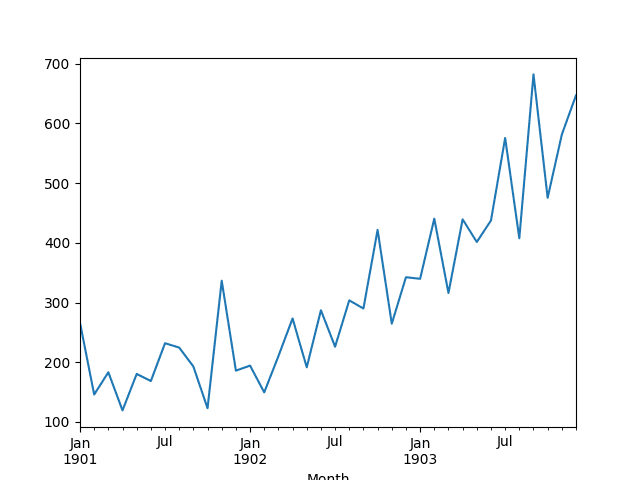
洗发水销售数据集的折线图

接下来，我们将看一下实验中使用的模型配置和测试工具。

实验测试框架

本节将介绍本教程中使用的测试框架。

数据分割

我们将把洗发水销售数据集分为两部分：训练集和测试集。

前两年的数据将用于训练数据集，剩下的一年数据将用于测试集。

模型将使用训练数据集进行开发，并对测试数据集进行预测。

在测试数据集上的持久性预测（朴素预测）实现了136.761个月洗发水销量的误差。这为测试集上的性能提供了一个可接受的较低界限。

模型评估

将使用滚动预测方案，也称为向前验证模型。

测试数据集的每个时间步都会逐一进行。模型将用于预测时间步，然后将测试集中实际的预期值取出，并将其提供给模型以预测下一个时间步。

这模拟了现实世界场景，其中每个月都会有新的洗发水销售观察值，并用于预测下个月。

这将通过训练和测试数据集的结构进行模拟。

将收集测试数据集上的所有预测，并计算误差分数以总结模型的技能。将使用均方根误差（RMSE），因为它会惩罚较大的误差，并产生一个与预测数据单位相同的分数，即月度洗发水销量。

数据准备

在将模型拟合到数据集之前，我们必须转换数据。

在拟合模型和进行预测之前，对数据集执行以下三种数据转换。

转换时间序列数据使其平稳。具体来说，使用 lag=1 的差分来消除数据中不断增长的趋势。
将时间序列转换为监督学习问题。具体来说，将数据组织成输入和输出模式，其中前一个时间步的观测值用作当前时间步观测值预测的输入。
转换观测值以具有特定的尺度。具体来说，将数据重新缩放到 -1 到 1 之间的值。

在计算误差分数之前，这些转换将被应用于预测中，以将它们恢复到其原始尺度。

LSTM 模型

我们将使用一个基础的状态LSTM模型，包含1个神经元，训练1000个周期。

理想情况下，应使用 batch size of 1 进行前向验证。我们将假设前向验证，并为了速度预测全年。因此，我们可以使用任何可被样本数量整除的 batch size，在这种情况下，我们将使用值 4。

理想情况下，会使用更多的训练周期（例如1500个），但为了使运行时间合理，此处截断为1000个。

模型将使用高效的ADAM优化算法和均方误差损失函数进行拟合。

实验运行

每个实验场景将运行 30 次，并从每次运行的末尾记录测试集上的 RMSE 分数。

让我们开始实验。

基线 LSTM 模型

让我们从基线 LSTM 模型开始。

此问题的基线 LSTM 模型具有以下配置：

滞后输入：1
训练轮数：1000
LSTM 隐藏层中的单元数：3
批次大小：4
重复次数：3

完整的代码列表如下。

此代码列表将作为所有后续实验的基础，仅在后续章节中提供对该代码的更改。

from pandas import DataFrame
from pandas import Series
from pandas import concat
from pandas import read_csv
from pandas import datetime
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.regularizers import L1L2
from math import sqrt
import matplotlib
# be able to save images on server
matplotlib.use('Agg')
from matplotlib import pyplot
import numpy

# date-time parsing function for loading the dataset
def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')

# frame a sequence as a supervised learning problem
def timeseries_to_supervised(data, lag=1):
	df = DataFrame(data)
	columns = [df.shift(i) for i in range(1, lag+1)]
	columns.append(df)
	df = concat(columns, axis=1)
	return df

# create a differenced series
def difference(dataset, interval=1):
	diff = list()
	for i in range(interval, len(dataset)):
		value = dataset[i] - dataset[i - interval]
		diff.append(value)
	return Series(diff)

# invert differenced value
def inverse_difference(history, yhat, interval=1):
	return yhat + history[-interval]

# scale train and test data to [-1, 1]
def scale(train, test):
	# fit scaler
	scaler = MinMaxScaler(feature_range=(-1, 1))
	scaler = scaler.fit(train)
	# transform train
	train = train.reshape(train.shape[0], train.shape[1])
	train_scaled = scaler.transform(train)
	# transform test
	test = test.reshape(test.shape[0], test.shape[1])
	test_scaled = scaler.transform(test)
	return scaler, train_scaled, test_scaled

# inverse scaling for a forecasted value
def invert_scale(scaler, X, yhat):
	new_row = [x for x in X] + [yhat]
	array = numpy.array(new_row)
	array = array.reshape(1, len(array))
	inverted = scaler.inverse_transform(array)
	return inverted[0, -1]

# fit an LSTM network to training data
def fit_lstm(train, n_batch, nb_epoch, n_neurons):
	X, y = train[:, 0:-1], train[:, -1]
	X = X.reshape(X.shape[0], 1, X.shape[1])
	model = Sequential()
	model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True))
	model.add(Dense(1))
	model.compile(loss='mean_squared_error', optimizer='adam')
	for i in range(nb_epoch):
		model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)
		model.reset_states()
	return model

# run a repeated experiment
def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons):
	# transform data to be stationary
	raw_values = series.values
	diff_values = difference(raw_values, 1)
	# transform data to be supervised learning
	supervised = timeseries_to_supervised(diff_values, n_lag)
	supervised_values = supervised.values[n_lag:,:]
	# split data into train and test-sets
	train, test = supervised_values[0:-12], supervised_values[-12:]
	# transform the scale of the data
	scaler, train_scaled, test_scaled = scale(train, test)
	# run experiment
	error_scores = list()
	for r in range(n_repeats):
		# fit the model
		train_trimmed = train_scaled[2:, :]
		lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons)
		# forecast test dataset
		test_reshaped = test_scaled[:,0:-1]
		test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1)
		output = lstm_model.predict(test_reshaped, batch_size=n_batch)
		predictions = list()
		for i in range(len(output)):
			yhat = output[i,0]
			X = test_scaled[i, 0:-1]
			# invert scaling
			yhat = invert_scale(scaler, X, yhat)
			# invert differencing
			yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)
			# store forecast
			predictions.append(yhat)
		# report performance
		rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))
		print('%d) Test RMSE: %.3f' % (r+1, rmse))
		error_scores.append(rmse)
	return error_scores

# configure the experiment
def run():
	# load dataset
	series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
	# configure the experiment
	n_lag = 1
	n_repeats = 30
	n_epochs = 1000
	n_batch = 4
	n_neurons = 3
	# run the experiment
	results = DataFrame()
	results['results'] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons)
	# summarize results
	print(results.describe())
	# save boxplot
	results.boxplot()
	pyplot.savefig('experiment_baseline.png')

# entry point
run()

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

from pandas import DataFrame

from pandas import Series

从 pandas 导入 concat

from pandas import read_csv

from pandas import datetime

from sklearn.metrics import mean_squared_error

从 sklearn.预处理导入 MinMaxScaler

from keras.models import Sequential

from keras.layers import Dense

从 keras.layers 导入 LSTM

from keras.regularizers import L1L2

from math import sqrt

import matplotlib

# 能够在服务器上保存图像

matplotlib.use('Agg')

from matplotlib import pyplot

import numpy

# 用于加载数据集的日期时间解析函数

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

# 将序列构造成监督学习问题

def timeseries_to_supervised(data, lag=1):

df = DataFrame(data)

columns = [df.shift(i) for i in range(1, lag+1)]

columns.append(df)

df = concat(columns, axis=1)

return df

# 创建差分序列

def difference(dataset, interval=1):

diff = list()

for i in range(interval, len(dataset)):

value = dataset[i] - dataset[i - interval]

diff.append(value)

return Series(diff)

# 反转差分值

def inverse_difference(history, yhat, interval=1):

return yhat + history[-interval]

# 将训练和测试数据缩放到 [-1, 1]

def scale(train, test):

# 拟合缩放器

scaler = MinMaxScaler(feature_range=(-1, 1))

scaler = scaler.fit(train)

# 转换训练集

train = train.reshape(train.shape[0], train.shape[1])

train_scaled = scaler.transform(train)

# 转换测试集

test = test.reshape(test.shape[0], test.shape[1])

test_scaled = scaler.transform(test)

return scaler, train_scaled, test_scaled

# 预测值的逆缩放

def invert_scale(scaler, X, yhat):

new_row = [x for x in X] + [yhat]

array = numpy.array(new_row)

array = array.reshape(1, len(array))

inverted = scaler.inverse_transform(array)

return inverted[0, -1]

# 训练一个 LSTM 网络

def fit_lstm(train, n_batch, nb_epoch, n_neurons):

X, y = train[:, 0:-1], train[:, -1]

X = X.reshape(X.shape[0], 1, X.shape[1])

model = Sequential()

model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True))

model.add(Dense(1))

model.compile(loss='mean_squared_error', optimizer='adam')

for i in range(nb_epoch):

model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)

model.reset_states()

return model

# 运行重复实验

def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons):

# 将数据转换为平稳

raw_values = series.values

diff_values = difference(raw_values, 1)

# 将数据转换为监督学习

supervised = timeseries_to_supervised(diff_values, n_lag)

supervised_values = supervised.values[n_lag:, :]

# 将数据分割成训练集和测试集

train, test = supervised_values[0:-12], supervised_values[-12:]

# 转换数据尺度

scaler, train_scaled, test_scaled = scale(train, test)

# 运行实验

error_scores = list()

for r in range(n_repeats):

# 拟合模型

train_trimmed = train_scaled[2:, :]

lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons)

# 预测测试数据集

test_reshaped = test_scaled[:,0:-1]

test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1)

output = lstm_model.predict(test_reshaped, batch_size=n_batch)

predictions = list()

for i in range(len(output)):

yhat = output[i,0]

X = test_scaled[i, 0:-1]

# 反转缩放

yhat = invert_scale(scaler, X, yhat)

# 反转差分

yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)

# 存储预测

predictions.append(yhat)

# 报告性能

rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))

print('%d) Test RMSE: %.3f' % (r+1, rmse))

error_scores.append(rmse)

return error_scores

# 配置实验

def run():

# 加载数据集

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 配置实验

n_lag = 1

n_repeats = 30

n_epochs = 1000

n_batch = 4

n_neurons = 3

# 运行实验

results = DataFrame()

results['results'] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons)

# 总结结果

print(results.describe())

# 保存箱线图

results.boxplot()

pyplot.savefig('experiment_baseline.png')

# 入口点

run()

运行实验会打印所有重复测试 RMSE 的汇总统计信息。

注意：您的结果可能会有所不同，这取决于算法或评估程序的随机性质，或者数值精度的差异。请考虑运行几次示例并比较平均结果。

我们可以看到，平均而言，此模型配置在测试 RMSE 上约为 92 个月度洗发水销量，标准差为 5。

          results
count   30.000000
mean    92.842537
std      5.748456
min     81.205979
25%     89.514367
50%     92.030003
75%     96.926145
max    105.247117

results

count 30.000000

平均值 92.842537

标准差 5.748456

最小值 81.205979

25% 89.514367

50% 92.030003

75% 96.926145

最大值 105.247117

还会根据测试 RMSE 结果的分布创建一个箱线图并将其保存到文件中。

该图清晰地描绘了结果的分布，重点突出了中间 50% 的值（盒子）和中位数（绿线）。

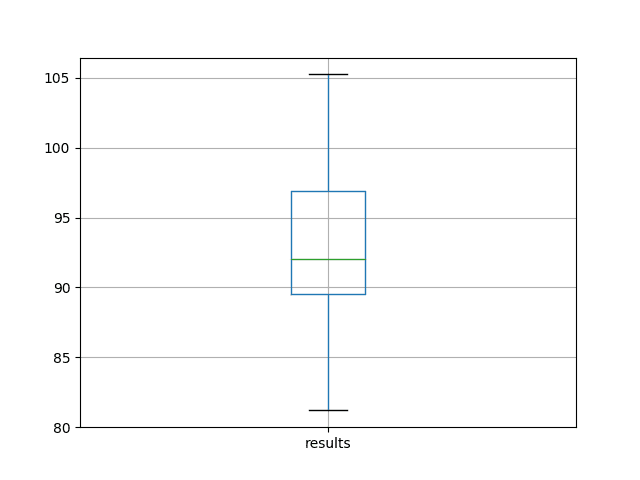
Box and Whisker Plot of Baseline Performance on the Shampoo Sales Dataset

洗发水销量数据集上基线性能的箱线图

偏置加权正则化

加权正则化可以应用于 LSTM 节点内的偏置连接。

在 Keras 中，这在创建 LSTM 层时通过 `bias_regularizer` 参数指定。正则化器被定义为 L1、L2 或 L1L2 类的一个实例。

更多细节在此

Keras 的正则化器用法

在此实验中，我们将比较 L1、L2 和 L1L2（默认为 0.01）与基线模型。我们可以使用 L1L2 类指定所有配置，如下所示：

L1L2(0.0, 0.0) [例如：基线]
L1L2(0.01, 0.0) [例如：L1]
L1L2(0.0, 0.01) [例如：L2]
L1L2(0.01, 0.01) [例如：L1L2 或弹性网]

下面列出了使用 LSTM 进行偏置加权正则化的更新后的 `fit_lstm()`、`experiment()` 和 `run()` 函数。

# fit an LSTM network to training data
def fit_lstm(train, n_batch, nb_epoch, n_neurons, reg):
	X, y = train[:, 0:-1], train[:, -1]
	X = X.reshape(X.shape[0], 1, X.shape[1])
	model = Sequential()
	model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True, bias_regularizer=reg))
	model.add(Dense(1))
	model.compile(loss='mean_squared_error', optimizer='adam')
	for i in range(nb_epoch):
		model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)
		model.reset_states()
	return model

# run a repeated experiment
def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg):
	# transform data to be stationary
	raw_values = series.values
	diff_values = difference(raw_values, 1)
	# transform data to be supervised learning
	supervised = timeseries_to_supervised(diff_values, n_lag)
	supervised_values = supervised.values[n_lag:,:]
	# split data into train and test-sets
	train, test = supervised_values[0:-12], supervised_values[-12:]
	# transform the scale of the data
	scaler, train_scaled, test_scaled = scale(train, test)
	# run experiment
	error_scores = list()
	for r in range(n_repeats):
		# fit the model
		train_trimmed = train_scaled[2:, :]
		lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons, reg)
		# forecast test dataset
		test_reshaped = test_scaled[:,0:-1]
		test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1)
		output = lstm_model.predict(test_reshaped, batch_size=n_batch)
		predictions = list()
		for i in range(len(output)):
			yhat = output[i,0]
			X = test_scaled[i, 0:-1]
			# invert scaling
			yhat = invert_scale(scaler, X, yhat)
			# invert differencing
			yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)
			# store forecast
			predictions.append(yhat)
		# report performance
		rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))
		print('%d) Test RMSE: %.3f' % (r+1, rmse))
		error_scores.append(rmse)
	return error_scores

# configure the experiment
def run():
	# load dataset
	series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
	# configure the experiment
	n_lag = 1
	n_repeats = 30
	n_epochs = 1000
	n_batch = 4
	n_neurons = 3
	regularizers = [L1L2(l1=0.0, l2=0.0), L1L2(l1=0.01, l2=0.0), L1L2(l1=0.0, l2=0.01), L1L2(l1=0.01, l2=0.01)]
	# run the experiment
	results = DataFrame()
	for reg in regularizers:
		name = ('l1 %.2f,l2 %.2f' % (reg.l1, reg.l2))
		results[name] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg)
	# summarize results
	print(results.describe())
	# save boxplot
	results.boxplot()
	pyplot.savefig('experiment_reg_bias.png')

# 训练一个 LSTM 网络

def fit_lstm(train, n_batch, nb_epoch, n_neurons, reg):

X, y = train[:, 0:-1], train[:, -1]

X = X.reshape(X.shape[0], 1, X.shape[1])

model = Sequential()

model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True, bias_regularizer=reg))

model.add(Dense(1))

model.compile(loss='mean_squared_error', optimizer='adam')

for i in range(nb_epoch):

model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)

model.reset_states()

return model

# 运行重复实验

def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg):

# 将数据转换为平稳

raw_values = series.values

diff_values = difference(raw_values, 1)

# 将数据转换为监督学习

supervised = timeseries_to_supervised(diff_values, n_lag)

supervised_values = supervised.values[n_lag:, :]

# 将数据分割成训练集和测试集

train, test = supervised_values[0:-12], supervised_values[-12:]

# 转换数据尺度

scaler, train_scaled, test_scaled = scale(train, test)

# 运行实验

error_scores = list()

for r in range(n_repeats):

# 拟合模型

train_trimmed = train_scaled[2:, :]

lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons, reg)

# 预测测试数据集

test_reshaped = test_scaled[:,0:-1]

test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1)

output = lstm_model.predict(test_reshaped, batch_size=n_batch)

predictions = list()

for i in range(len(output)):

yhat = output[i,0]

X = test_scaled[i, 0:-1]

# 反转缩放

yhat = invert_scale(scaler, X, yhat)

# 反转差分

yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)

# 存储预测

predictions.append(yhat)

# 报告性能

rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))

print('%d) Test RMSE: %.3f' % (r+1, rmse))

error_scores.append(rmse)

return error_scores

# 配置实验

def run():

# 加载数据集

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 配置实验

n_lag = 1

n_repeats = 30

n_epochs = 1000

n_batch = 4

n_neurons = 3

regularizers = [L1L2(l1=0.0, l2=0.0), L1L2(l1=0.01, l2=0.0), L1L2(l1=0.0, l2=0.01), L1L2(l1=0.01, l2=0.01)]

# 运行实验

results = DataFrame()

for reg in regularizers:

name = ('l1 %.2f,l2 %.2f' % (reg.l1, reg.l2))

results[name] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg)

# 总结结果

print(results.describe())

# 保存箱线图

results.boxplot()

pyplot.savefig('experiment_reg_bias.png')

运行此实验将打印每个评估配置的描述性统计信息。

注意：您的结果可能会有所不同，这取决于算法或评估程序的随机性质，或者数值精度的差异。请考虑运行几次示例并比较平均结果。

结果表明，平均而言，默认情况下不进行偏差正则化可带来比所有其他考虑的配置更好的性能。

       l1 0.00,l2 0.00  l1 0.01,l2 0.00  l1 0.00,l2 0.01  l1 0.01,l2 0.01
count        30.000000        30.000000        30.000000        30.000000
mean         92.821489        95.520003        93.285389        92.901021
std           4.894166         3.637022         3.906112         5.082358
min          81.394504        89.477398        82.994480        78.729224
25%          89.356330        93.017723        90.907343        91.210105
50%          92.822871        95.502700        93.837562        94.525965
75%          95.899939        98.195980        95.426270        96.882378
max         101.194678       101.750900       100.650130        97.766301

l1 0.00,l2 0.00 l1 0.01,l2 0.00 l1 0.00,l2 0.01 l1 0.01,l2 0.01

count 30.000000 30.000000 30.000000 30.000000

mean 92.821489 95.520003 93.285389 92.901021

std 4.894166 3.637022 3.906112 5.082358

min 81.394504 89.477398 82.994480 78.729224

25% 89.356330 93.017723 90.907343 91.210105

50% 92.822871 95.502700 93.837562 94.525965

75% 95.899939 98.195980 95.426270 96.882378

max 101.194678 101.750900 100.650130 97.766301

还创建了一个箱须图来比较每种配置结果的分布。

该图显示，所有配置的分布范围大致相同，而在此问题上，增加偏差正则化并没有普遍带来帮助。

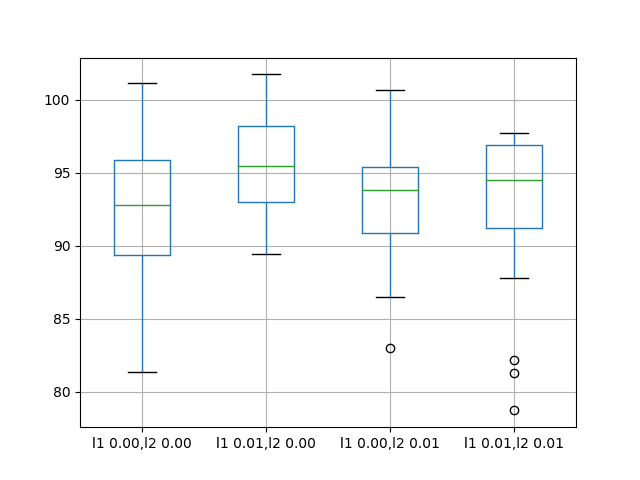
Box and Whisker Plots of Bias Weight Regularization Performance on the Shampoo Sales Dataset

香波销售数据集上偏差权重正则化性能的箱须图

输入加权正则化

我们还可以对每个 LSTM 单元的输入连接应用正则化。

在 Keras 中，这是通过将 `kernel_regularizer` 参数设置为正则化器类来实现的。

我们将测试与上一节相同的正则化器配置，具体来说

L1L2(0.0, 0.0) [例如：基线]
L1L2(0.01, 0.0) [例如：L1]
L1L2(0.0, 0.01) [例如：L2]
L1L2(0.01, 0.01) [例如：L1L2 或弹性网]

下面列出了使用 LSTM 进行偏置加权正则化的更新后的 `fit_lstm()`、`experiment()` 和 `run()` 函数。

# fit an LSTM network to training data
def fit_lstm(train, n_batch, nb_epoch, n_neurons, reg):
	X, y = train[:, 0:-1], train[:, -1]
	X = X.reshape(X.shape[0], 1, X.shape[1])
	model = Sequential()
	model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True, kernel_regularizer=reg))
	model.add(Dense(1))
	model.compile(loss='mean_squared_error', optimizer='adam')
	for i in range(nb_epoch):
		model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)
		model.reset_states()
	return model

# run a repeated experiment
def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg):
	# transform data to be stationary
	raw_values = series.values
	diff_values = difference(raw_values, 1)
	# transform data to be supervised learning
	supervised = timeseries_to_supervised(diff_values, n_lag)
	supervised_values = supervised.values[n_lag:,:]
	# split data into train and test-sets
	train, test = supervised_values[0:-12], supervised_values[-12:]
	# transform the scale of the data
	scaler, train_scaled, test_scaled = scale(train, test)
	# run experiment
	error_scores = list()
	for r in range(n_repeats):
		# fit the model
		train_trimmed = train_scaled[2:, :]
		lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons, reg)
		# forecast test dataset
		test_reshaped = test_scaled[:,0:-1]
		test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1)
		output = lstm_model.predict(test_reshaped, batch_size=n_batch)
		predictions = list()
		for i in range(len(output)):
			yhat = output[i,0]
			X = test_scaled[i, 0:-1]
			# invert scaling
			yhat = invert_scale(scaler, X, yhat)
			# invert differencing
			yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)
			# store forecast
			predictions.append(yhat)
		# report performance
		rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))
		print('%d) Test RMSE: %.3f' % (r+1, rmse))
		error_scores.append(rmse)
	return error_scores

# configure the experiment
def run():
	# load dataset
	series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
	# configure the experiment
	n_lag = 1
	n_repeats = 30
	n_epochs = 1000
	n_batch = 4
	n_neurons = 3
	regularizers = [L1L2(l1=0.0, l2=0.0), L1L2(l1=0.01, l2=0.0), L1L2(l1=0.0, l2=0.01), L1L2(l1=0.01, l2=0.01)]
	# run the experiment
	results = DataFrame()
	for reg in regularizers:
		name = ('l1 %.2f,l2 %.2f' % (reg.l1, reg.l2))
		results[name] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg)
	# summarize results
	print(results.describe())
	# save boxplot
	results.boxplot()
	pyplot.savefig('experiment_reg_input.png')

# 训练一个 LSTM 网络

def fit_lstm(train, n_batch, nb_epoch, n_neurons, reg):

X, y = train[:, 0:-1], train[:, -1]

X = X.reshape(X.shape[0], 1, X.shape[1])

model = Sequential()

model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True, kernel_regularizer=reg))

model.add(Dense(1))

model.compile(loss='mean_squared_error', optimizer='adam')

for i in range(nb_epoch):

model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)

model.reset_states()

return model

# 运行重复实验

def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg):

# 将数据转换为平稳

raw_values = series.values

diff_values = difference(raw_values, 1)

# 将数据转换为监督学习

supervised = timeseries_to_supervised(diff_values, n_lag)

supervised_values = supervised.values[n_lag:, :]

# 将数据分割成训练集和测试集

train, test = supervised_values[0:-12], supervised_values[-12:]

# 转换数据尺度

scaler, train_scaled, test_scaled = scale(train, test)

# 运行实验

error_scores = list()

for r in range(n_repeats):

# 拟合模型

train_trimmed = train_scaled[2:, :]

lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons, reg)

# 预测测试数据集

test_reshaped = test_scaled[:,0:-1]

test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1)

output = lstm_model.predict(test_reshaped, batch_size=n_batch)

predictions = list()

for i in range(len(output)):

yhat = output[i,0]

X = test_scaled[i, 0:-1]

# 反转缩放

yhat = invert_scale(scaler, X, yhat)

# 反转差分

yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)

# 存储预测

predictions.append(yhat)

# 报告性能

rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))

print('%d) Test RMSE: %.3f' % (r+1, rmse))

error_scores.append(rmse)

return error_scores

# 配置实验

def run():

# 加载数据集

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 配置实验

n_lag = 1

n_repeats = 30

n_epochs = 1000

n_batch = 4

n_neurons = 3

regularizers = [L1L2(l1=0.0, l2=0.0), L1L2(l1=0.01, l2=0.0), L1L2(l1=0.0, l2=0.01), L1L2(l1=0.01, l2=0.01)]

# 运行实验

results = DataFrame()

for reg in regularizers:

name = ('l1 %.2f,l2 %.2f' % (reg.l1, reg.l2))

results[name] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg)

# 总结结果

print(results.describe())

# 保存箱线图

results.boxplot()

pyplot.savefig('experiment_reg_input.png')

运行此实验将打印每个评估配置的描述性统计信息。

注意：您的结果可能会有所不同，这取决于算法或评估程序的随机性质，或者数值精度的差异。请考虑运行几次示例并比较平均结果。

结果表明，在此设置下，将权重正则化添加到输入连接确实提供了普遍的好处。

我们可以看到，对于所有配置，测试 RMSE 大约降低了 10 个单位，并且可能在 L1 和 L2 合并为弹性网络类型约束时带来更多好处。

       l1 0.00,l2 0.00  l1 0.01,l2 0.00  l1 0.00,l2 0.01  l1 0.01,l2 0.01
count        30.000000        30.000000        30.000000        30.000000
mean         91.640028        82.118980        82.137198        80.471685
std           6.086401         4.116072         3.378984         2.212213
min          80.392310        75.705210        76.005173        76.550909
25%          88.025135        79.237822        79.698162        78.780802
50%          91.843761        81.235433        81.463882        80.283913
75%          94.860117        85.510177        84.563980        82.443390
max         105.820586        94.210503        90.823454        85.243135

l1 0.00,l2 0.00 l1 0.01,l2 0.00 l1 0.00,l2 0.01 l1 0.01,l2 0.01

count 30.000000 30.000000 30.000000 30.000000

mean 91.640028 82.118980 82.137198 80.471685

std 6.086401 4.116072 3.378984 2.212213

min 80.392310 75.705210 76.005173 76.550909

25% 88.025135 79.237822 79.698162 78.780802

50% 91.843761 81.235433 81.463882 80.283913

75% 94.860117 85.510177 84.563980 82.443390

max 105.820586 94.210503 90.823454 85.243135

还创建了一个箱须图来比较每种配置结果的分布。

该图显示了输入正则化误差的总体较低分布。结果还表明，正则化结果的分布更紧密，可能在获得更好结果的 L1L2 配置中更为明显。

这是一个令人鼓舞的发现，表明对输入正则化使用不同的 L1L2 值进行额外实验是值得研究的。

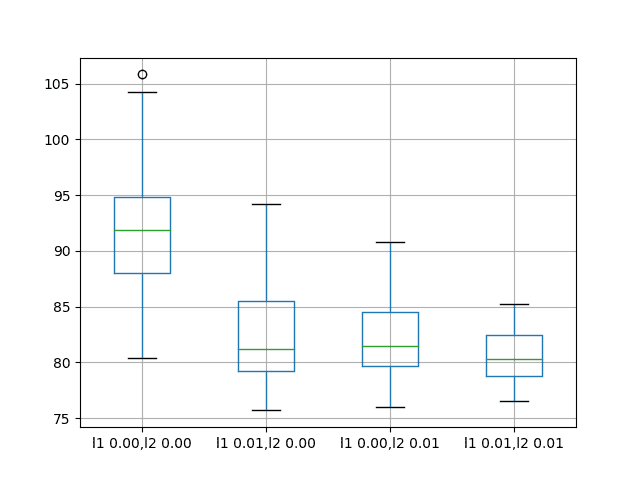
Box and Whisker Plots of Input Weight Regularization Performance on the Shampoo Sales Dataset

香波销售数据集上输入权重正则化性能的箱须图

循环加权正则化

最后，我们还可以对每个 LSTM 单元的循环连接应用正则化。

在 Keras 中，这是通过将 `recurrent_regularizer` 参数设置为正则化器类来实现的。

我们将测试与上一节相同的正则化器配置，具体来说

L1L2(0.0, 0.0) [例如：基线]
L1L2(0.01, 0.0) [例如：L1]
L1L2(0.0, 0.01) [例如：L2]
L1L2(0.01, 0.01) [例如：L1L2 或弹性网]

下面列出了使用 LSTM 进行偏置加权正则化的更新后的 `fit_lstm()`、`experiment()` 和 `run()` 函数。

# fit an LSTM network to training data
def fit_lstm(train, n_batch, nb_epoch, n_neurons, reg):
	X, y = train[:, 0:-1], train[:, -1]
	X = X.reshape(X.shape[0], 1, X.shape[1])
	model = Sequential()
	model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True, recurrent_regularizer=reg))
	model.add(Dense(1))
	model.compile(loss='mean_squared_error', optimizer='adam')
	for i in range(nb_epoch):
		model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)
		model.reset_states()
	return model

# run a repeated experiment
def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg):
	# transform data to be stationary
	raw_values = series.values
	diff_values = difference(raw_values, 1)
	# transform data to be supervised learning
	supervised = timeseries_to_supervised(diff_values, n_lag)
	supervised_values = supervised.values[n_lag:,:]
	# split data into train and test-sets
	train, test = supervised_values[0:-12], supervised_values[-12:]
	# transform the scale of the data
	scaler, train_scaled, test_scaled = scale(train, test)
	# run experiment
	error_scores = list()
	for r in range(n_repeats):
		# fit the model
		train_trimmed = train_scaled[2:, :]
		lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons, reg)
		# forecast test dataset
		test_reshaped = test_scaled[:,0:-1]
		test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1)
		output = lstm_model.predict(test_reshaped, batch_size=n_batch)
		predictions = list()
		for i in range(len(output)):
			yhat = output[i,0]
			X = test_scaled[i, 0:-1]
			# invert scaling
			yhat = invert_scale(scaler, X, yhat)
			# invert differencing
			yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)
			# store forecast
			predictions.append(yhat)
		# report performance
		rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))
		print('%d) Test RMSE: %.3f' % (r+1, rmse))
		error_scores.append(rmse)
	return error_scores

# configure the experiment
def run():
	# load dataset
	series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
	# configure the experiment
	n_lag = 1
	n_repeats = 30
	n_epochs = 1000
	n_batch = 4
	n_neurons = 3
	regularizers = [L1L2(l1=0.0, l2=0.0), L1L2(l1=0.01, l2=0.0), L1L2(l1=0.0, l2=0.01), L1L2(l1=0.01, l2=0.01)]
	# run the experiment
	results = DataFrame()
	for reg in regularizers:
		name = ('l1 %.2f,l2 %.2f' % (reg.l1, reg.l2))
		results[name] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg)
	# summarize results
	print(results.describe())
	# save boxplot
	results.boxplot()
	pyplot.savefig('experiment_reg_recurrent.png')

# 训练一个 LSTM 网络

def fit_lstm(train, n_batch, nb_epoch, n_neurons, reg):

X, y = train[:, 0:-1], train[:, -1]

X = X.reshape(X.shape[0], 1, X.shape[1])

model = Sequential()

model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True, recurrent_regularizer=reg))

model.add(Dense(1))

model.compile(loss='mean_squared_error', optimizer='adam')

for i in range(nb_epoch):

model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)

model.reset_states()

return model

# 运行重复实验

def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg):

# 将数据转换为平稳

raw_values = series.values

diff_values = difference(raw_values, 1)

# 将数据转换为监督学习

supervised = timeseries_to_supervised(diff_values, n_lag)

supervised_values = supervised.values[n_lag:, :]

# 将数据分割成训练集和测试集

train, test = supervised_values[0:-12], supervised_values[-12:]

# 转换数据尺度

scaler, train_scaled, test_scaled = scale(train, test)

# 运行实验

error_scores = list()

for r in range(n_repeats):

# 拟合模型

train_trimmed = train_scaled[2:, :]

lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons, reg)

# 预测测试数据集

test_reshaped = test_scaled[:,0:-1]

test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1)

output = lstm_model.predict(test_reshaped, batch_size=n_batch)

predictions = list()

for i in range(len(output)):

yhat = output[i,0]

X = test_scaled[i, 0:-1]

# 反转缩放

yhat = invert_scale(scaler, X, yhat)

# 反转差分

yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)

# 存储预测

predictions.append(yhat)

# 报告性能

rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))

print('%d) Test RMSE: %.3f' % (r+1, rmse))

error_scores.append(rmse)

return error_scores

# 配置实验

def run():

# 加载数据集

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 配置实验

n_lag = 1

n_repeats = 30

n_epochs = 1000

n_batch = 4

n_neurons = 3

regularizers = [L1L2(l1=0.0, l2=0.0), L1L2(l1=0.01, l2=0.0), L1L2(l1=0.0, l2=0.01), L1L2(l1=0.01, l2=0.01)]

# 运行实验

results = DataFrame()

for reg in regularizers:

name = ('l1 %.2f,l2 %.2f' % (reg.l1, reg.l2))

results[name] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, reg)

# 总结结果

print(results.describe())

# 保存箱线图

results.boxplot()

pyplot.savefig('experiment_reg_recurrent.png')

运行此实验将打印每个评估配置的描述性统计信息。

注意：您的结果可能会有所不同，这取决于算法或评估程序的随机性质，或者数值精度的差异。请考虑运行几次示例并比较平均结果。

结果表明，在此问题上，在 LSTM 上对循环连接使用正则化没有明显的益处。

所有尝试的变体的平均性能都比基线模型差。

       l1 0.00,l2 0.00  l1 0.01,l2 0.00  l1 0.00,l2 0.01  l1 0.01,l2 0.01
count        30.000000        30.000000        30.000000        30.000000
mean         92.918797       100.675386       101.302169        96.820026
std           7.172764         3.866547         5.228815         3.966710
min          72.967841        93.789854        91.063592        89.367600
25%          90.311185        98.014045        98.222732        94.787647
50%          92.327824       100.546756       101.903350        95.727549
75%          95.989761       103.491192       104.918266        98.240613
max         110.529422       108.788604       110.712064       111.185747

l1 0.00,l2 0.00 l1 0.01,l2 0.00 l1 0.00,l2 0.01 l1 0.01,l2 0.01

count 30.000000 30.000000 30.000000 30.000000

mean 92.918797 100.675386 101.302169 96.820026

std 7.172764 3.866547 5.228815 3.966710

min 72.967841 93.789854 91.063592 89.367600

25% 90.311185 98.014045 98.222732 94.787647

50% 92.327824 100.546756 101.903350 95.727549

75% 95.989761 103.491192 104.918266 98.240613

max 110.529422 108.788604 110.712064 111.185747

还创建了一个箱须图来比较每种配置结果的分布。

该图显示了与汇总统计数据相同的模式，表明使用循环权重正则化益处甚微。

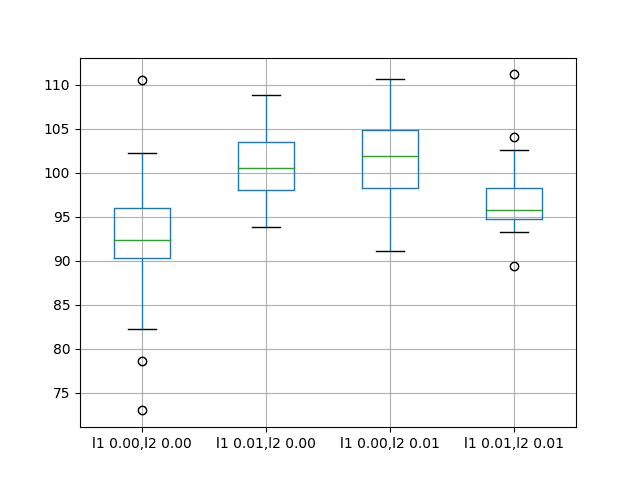
Box and Whisker Plots of Recurrent Weight Regularization Performance on the Shampoo Sales Dataset

香波销售数据集上循环权重正则化性能的箱须图

扩展

本节列出了跟进实验的思路，以扩展本教程的工作。

输入权重正则化。在此问题上，输入权重正则化的实验结果显示出巨大的潜力，可以列出性能。可以通过尝试网格搜索不同的 L1 和 L2 值来找到最佳配置，从而进一步研究这一点。
行为动态。可以通过绘制训练周期内的训练和测试 RMSE 来研究每种权重正则化方案的动态行为，以了解权重正则化对过拟合或欠拟合行为模式的影响。
组合正则化。可以设计实验来探索组合不同权重正则化方案的效果。
激活正则化。Keras 也支持激活正则化，这可能是探索对 LSTM 施加约束和减少过拟合的另一个途径。

总结

在本教程中，您学习了如何为时间序列预测使用 LSTM 进行权重正则化。

具体来说，你学到了：

如何设计一个健壮的测试框架来评估 LSTM 网络在时间序列预测中的表现。
如何为时间序列预测配置 LSTM 的偏差权重正则化。
如何为时间序列预测配置 LSTM 的输入和循环权重正则化。

关于使用 LSTM 网络进行权重正则化，您有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

如何使用统计显著性检验来解释机器学习结果

如何将时间序列转换为 Python 中的监督学习问题

65 条对使用 LSTM 网络进行时间序列预测的权重正则化的回复

Alex 2017 年 5 月 5 日上午 5:57 #

每次都做得很好。

但我想了解为什么我们总是使用 RMSE，而不使用准确率指标？？

回复
- Jason Brownlee 2017 年 5 月 5 日上午 7:35 #
  
  您无法在回归问题上衡量准确率（除非您将其转换为分类问题）。
  
  一般来说，输出变量为实数值的问题是回归问题，输出为类别或标签的问题是分类问题。
  
  回复
Alex 2017 年 5 月 5 日上午 7:51 #

啊，好的，是的，这是逻辑思维。谢谢

回复
shobhit 2017 年 5 月 5 日晚上 9:08 #

你好，杰森，
如何使用多个列的输入和单个列的输出来预测股票市场数据。

回复
- Jason Brownlee 2017 年 5 月 6 日上午 7:42 #
  
  每个单独的时间序列将被构建为 LSTM 中的一个单独的特征。
  
  另外，我认为短期证券价格是随机游走且无法预测的。
  https://machinelearning.org.cn/gentle-introduction-random-walk-times-series-forecasting-python/
  
  回复
shobhit 2017 年 5 月 5 日晚上 9:18 #

import numpy as np
import pandas as pd
import tensorflow as tf
#tf.logging.set_verosity(tf.logging.ERROR)
from pandas_datareader import data as web
import matplotlib.pyplot as plt
def get_data()
feature_cols={‘ret_%s’ %i:tf.constant(idata[‘ret_%s’%i].values)for i in lags}
labels=tf.constant((idata[‘returns’]>0).astype(int).values,shape=[idata[‘returns’].size,1])
return feature_cols,labels

symbol=’^GSPC’
data=web.DataReader(symbol,data_source=’yahoo’,start=’2014-01-01′,end=’2016-10-31′)[‘Adj Close’]
data=pd.DataFrame(data)
data.rename(columns={‘Adj Close’:’price’},inplace=True)
data[‘returns’]=np.log(data/data.shift(1))
lags=range(1,6)
for i in lags
data[‘ret_%s’% i]=np.sign(data[‘returns’].shift(i))
data.dropna(inplace=True)
print data.round(4).tail()
cutoff=’2015-1-1′
training_data=data[data.index=cutoff].copy()
#def get_data()
#feature_cols={‘ret_%s’ %i:tf.constant(data[‘ret_%s’%i].values)for i in lags}
#labels=tf.constant((data[‘returns’]>0).astype(int).values,shape=[data[‘returns’].size,1])
#return feature_cols,labels
fc=[tf.contrib.layers.real_valued_column(‘ret_%s’% i,dimension=1) for i in lags]
model=tf.contrib.learn.DNNClassifier(feature_columns=fc,n_classes=2,hidden_units=[100,100])
idata=training_data
model.fit(input_fn=get_data,steps=500)
model.evaluate(input_fn=get_data,steps=1)
pred=model.predict(input_fn=get_data)
pred[:30]
training_data[‘prediction’]=np.where(pred>0,1,-1)
training_data[‘strategy’]=training_data[‘prediction’]*training_data[‘returns’]
training_data[[‘returns’,’strategy’]].cumsum().apply(np.exp).plot(figsize=(10,6))
idata=test_data
model.evaluate(input_fn=get_data,steps=1)
pred=model.predict(input_fn=get_data)
test_data[‘prediction’]=np.where(pred>0,1,-1)
test_data[‘strategy’]=test_data[‘prediction’]*test_data[‘returns’]
test_data[[‘returns’,’strategy’]].cumsum().apply(np.exp).plot(figsize=(10,6))
#pred[:1]
if __name__ == ‘__main__’
get_data()

你好，杰森，
我刚运行了这段代码，但遇到了一些错误，无法理解错误。
错误是：-----> 1 pred[:30]

TypeError: ‘generator’ object is not subscriptable

请帮忙。

回复
- Jason Brownlee 2017 年 5 月 6 日上午 7:43 #
  
  也许可以联系您粘贴的 tensorflow 代码的作者？
  
  回复
Birkey 2017 年 5 月 10 日上午 10:48 #

好文！
然而，让我感到困惑的是，在 LSTM 模型部分，“批次大小为 1 是必需的，因为我们将使用前向验证并对测试数据的最后 12 个月中的每一个进行单步预测。”，但您使用的批次大小是 4 (n_batch=4)。

我猜您的意思是“需要时间步长为 1”，我说得对吗？因为每个月的预测意味着一个时间步长。

回复
- Jason Brownlee 2017 年 5 月 11 日上午 8:26 #
  
  你说得很有道理。
  
  如果我们对测试数据的每个时间步进行预测，那么需要 1 的批次大小。这里我们先预测一整年，然后通过预测来查看其含义。
  
  我已经更新了帖子，纠正了错误。
  
  回复
Laurent 2017 年 5 月 11 日下午 5:58 #

感谢您提供的所有教学资料，通过您的文章学习非常容易！

我有一个问题：在您所有的时间序列深度学习示例中，您总是预测下一个时间步，一次一个。

如何处理这种情况：使用时间序列进行训练，并预测接下来的 12 个时间步，例如？

回复
- Jason Brownlee 2017 年 5 月 12 日上午 7:37 #
  
  这里有一个例子
  https://machinelearning.org.cn/multi-step-time-series-forecasting-long-short-term-memory-networks-python/
  
  回复
jinhua zhang 2017 年 5 月 12 日上午 4:31 #

嗨，您的文章对我很有用！但是当我运行“偏差权重正则化过程”时，Spyder 会出现错误：“D:\Program Files\Anaconda3\lib\site-packages\matplotlib\__init__.py:1357: UserWarning: This call to matplotlib.use() has no effect
because the backend has already been chosen;
matplotlib.use() must be called *before* pylab, matplotlib.pyplot,
or matplotlib.backends is imported for the first time.

warnings.warn(_use_error_msg)”，
我不知道如何解决这个错误，您能帮我吗？

回复
- Jason Brownlee 2017 年 5 月 12 日上午 7:47 #
  
  您能尝试从命令行运行脚本而不是在 IDE 中运行吗？
  
  回复
  - jinhua zhang 2017 年 5 月 16 日上午 1:07 #
    
    非常感谢！因为我错过了命令
    “# entry point
    run()”。
    当我添加命令后，程序就可以运行了。
    
    回复
    - Jason Brownlee 2017 年 5 月 16 日上午 8:49 #
      
      很高兴听到这个消息。
      
      回复
Neeraj Agrawal 2017 年 10 月 31 日上午 6:17 #

我有一个关于 stateful = True 的疑问。正如 Keras 文档中所提到的，第一个批次的第一个元素与第二个批次的第一个元素等序列化。但您没有将时间序列转换为该顺序。这是正确的观察，还是我遗漏了什么？

回复
- conspiracypopcorn 2018 年 3 月 17 日上午 5:19 #
  
  我非常确定实现是错误的。如果您查看 Keras 手册，LSTM 的输入应该是 (batch_size, timesteps, input_dim)。问题是，在这个例子中我们只有一个序列，所以 batch_size 应该是 1，timesteps 应该是 4，而不是文章中显示的相反。那么，状态在批次之间保持不变也是有意义的。
  
  回复
SethM 2018 年 4 月 4 日上午 9:04 #

我正在尝试理解您如何将正则化器附加到模型。在 fit_lstm(...) 方法中，您实际上从未将 reg 变量的任何内容附加到模型。还是我遗漏了什么？谢谢！

回复
- Jason Brownlee 2018 年 4 月 5 日上午 5:46 #
  
  它们通过参数在 LSTM 层上指定。
  
  回复
  - SethM 2018 年 4 月 8 日上午 2:15 #
    
    谢谢！代码视图小部件隐藏了它，我的错！
    
    Seth
    
    回复
Rob 2018 年 5 月 5 日下午 2:14 #

感谢这篇帖子。您的帖子非常有价值，我感谢您花费时间撰写这些帖子。

您为什么选择 LSTM 的隐藏层数量为 3？总的来说，如何选择隐藏单元的数量？

回复
- Jason Brownlee 2018 年 5 月 6 日上午 6:22 #
  
  这是一个很好的问题。我做了一些试错。
  
  有关配置神经网络的更多信息，请参阅此内容
  https://machinelearning.org.cn/faq/single-faq/how-many-layers-and-nodes-do-i-need-in-my-neural-network
  
  回复
Rob 2018 年 5 月 7 日晚上 10:58 #

谢谢。

我想知道 LSTM 的隐藏层数量是否是模型输入样本数量的函数？也就是说，每个隐藏层都有需要学习的权重，如果数据较少，那么选择大量的隐藏层会倾向于过拟合。

另外，隐藏层的维度是多少？例如，如果输入形状是 (5,30) — (时间步数, 特征数)，样本数量是 100,000 ... 那么第一个隐藏层和后续 LSTM 层的维度会是多少？

此致，
-Avi

回复
- Jason Brownlee 2018 年 5 月 8 日上午 6:13 #
  
  不，第一个隐藏单元的数量与输入序列的长度无关。
  
  您可以通过打印 model.summary() 的输出来查看每个层的形状。
  
  回复
Brian McDermott 2018 年 9 月 6 日晚上 11:04 #

嗨，Jason，

感谢分享这篇文章。

我有一个拥有 3 个 LSTM 层的 LSTM 网络。我想知道是否需要在每个 LSTM 层上添加循环正则化？

回复
- Jason Brownlee 2018 年 9 月 7 日上午 8:04 #
  
  试试看吧。
  
  回复
Lee MH 2019 年 11 月 27 日下午 12:23 #

我已经看到了好的内容。

我可以亲自问您一个问题吗？您能否在 LSTM 的预测中强调特定变量？

当模型计算变量的权重时，您能使某个特定变量更重要吗？

回复
- Jason Brownlee 2019 年 11 月 27 日下午 1:51 #
  
  谢谢。
  
  不，模型会在学习过程中自行确定什么最重要。
  
  回复
Alok Singh 2020 年 1 月 24 日上午 1:26 #

嘿，感谢您的精彩解释！！

我的问题是
在您的偏差权重正则化代码和输入权重正则化代码之间有什么区别吗？因为在两者中，正则化的使用方式相似，系统将如何识别您想使用偏差正则化还是输入权重正则化？

回复
- Alok Singh 2020 年 1 月 24 日上午 1:27 #
  
  例如，对于 recurrent_regularizer，您已指定了它，但对于输入权重正则化呢？
  
  回复
- Alok Singh 2020 年 1 月 24 日上午 1:28 #
  
  哦！我明白了。
  
  感谢您的精彩博文。
  
  回复
  - Jason Brownlee 2020 年 1 月 24 日上午 7:54 #
    
    不客气。
    
    回复
- Jason Brownlee 2020 年 1 月 24 日上午 7:54 #
  
  对于偏差与权重正则化，LSTM 层使用了不同的参数。
  
  回复
Stephan 2020 年 2 月 17 日下午 2:18 #

布朗利博士您好，
我有一个关于验证的问题
在模型.fit() 中结合 validation_split 或 validation_data 参数的最佳方法是什么？也就是说，在训练期间进行验证以评估过拟合。
validation_split 似乎不起作用…

谢谢

回复
- Jason Brownlee 2020 年 2 月 18 日上午 6:15 #
  
  LSTM 的验证数据非常棘手。您最好使用前向验证。
  
  回复
AGGELOS PAPOUTSIS 2020 年 8 月 26 日上午 12:13 #

嗨，

您是否有关于应用偏差/权重或循环正则化时的内部程序的文章？先谢谢了。

回复
- AGGELOS PAPOUTSIS 2020 年 8 月 26 日上午 12:17 #
  
  换句话说，哪一部分最好进行正则化？
  
  回复
  - Jason Brownlee 2020 年 8 月 26 日上午 6:51 #
    
    我建议比较一系列正则化技术的结果。
    
    回复
- Jason Brownlee 2020 年 8 月 26 日上午 6:51 #
  
  这可能有助于作为起点
  https://machinelearning.org.cn/introduction-to-regularization-to-reduce-overfitting-and-improve-generalization-error/
  
  回复
Jessy 2020 年 11 月 28 日下午 7:39 #

扩展
本节列出了跟进实验的思路，以扩展本教程的工作。

激活正则化。Keras 也支持激活正则化，这可能是探索对 LSTM 施加约束和减少过拟合的另一个途径。

嗨，杰森，
我读了上面的工作。在其中您给出了一些扩展……特别是最后一项工作是激活正则化（激活函数正则化），对吗？我的意思是，我可以使用激活函数中的正则化技术来处理过拟合概念吗？我的理解是正确的还是错误的？

回复
- Jason Brownlee 2020 年 11 月 29 日上午 8:11 #
  
  是的，这里有一个例子
  https://machinelearning.org.cn/how-to-reduce-generalization-error-in-deep-neural-networks-with-activity-regularization-in-keras/
  
  回复
Jessy 2021 年 1 月 20 日上午 10:59 #

嗨，杰森，
我能否同时使用 LSTM 的权重正则化和隐藏层的激活正则化来克服过拟合？

回复
- Jason Brownlee 2021 年 1 月 20 日下午 12:41 #
  
  我看不出为什么不行，也许可以尝试一下，并将其结果与不使用它进行比较。
  
  回复
  - Jessy 2021 年 1 月 21 日下午 12:36 #
    
    嗨，杰森，
    是否可以将 LSTM + 权重正则化 + Dropout 技术结合使用以减少过拟合？
    
    回复
    - Jason Brownlee 2021年1月22日上午7:14 #
      
      是的，也许可以尝试组合以查看它在您的数据集上是否表现更好。
      
      回复
Jessy 2021年1月22日下午12:03 #

嗨，杰森，
是否可以将激活正则化用于LSTM节点以克服过拟合？

回复
- Jason Brownlee 2021年1月22日下午1:23 #
  
  可以与LSTM一起使用。
  
  这是否有助于防止过拟合，具体取决于您的模型和数据集的细节。
  
  回复
Jessy 2021年1月28日下午2:56 #

你好 Jason，
哪种正则化技术 L1（或）L2（或）ELASTIC NET 更适合 LSTM 模型？

回复
- Jason Brownlee 2021年1月29日上午5:59 #
  
  这取决于您的模型和数据集的细节。
  
  也许可以尝试多种方法，找出最适合您的方法。
  
  回复
Jessy 2021年1月28日下午7:04 #

嗨，杰森，
在 LSTM 输出层上使用 L1 正则化，并在隐藏（密集）层中使用 dropout 来构建一个泛化模型。

回复
- Jason Brownlee 2021年1月29日上午5:59 #
  
  这听起来很奇怪。通常，模型中只会使用一种正则化方法。
  
  回复
Peter 2021年1月29日下午7:33 #

嗨，Jason，

如果您发现深度模型需要批量归一化，但仍需要一些正则化来防止过拟合。应该测试哪些方法？

我读到 Dropout 不应与 Batch Norm 一起使用，我也读到（至少一些）Lx 正则化方法在与 Batch Norm 结合时起着另一个作用（https://blog.janestreet.com/l2-regularization-and-batch-norm/）。

根据您的经验，在使用批量归一化但仍存在过拟合的深度 LSTM 网络中，我应该从哪些方面开始实验？

我们还可以假设用于训练的更多数据已经用尽，并且数据增强是一个非常有限的选择。

回复
- Jason Brownlee 2021年1月30日上午6:32 #
  
  Dropout 仍然效果很好，早停和权重衰减也是如此。
  
  此外，使用较小的学习率和更多的 epoch 来减慢学习速度。
  
  总的来说，尝试几种方法，找出最适合您模型+数据的解决方案。
  
  回复
Jessy 2021年2月16日下午9:56 #

嗨，杰森，
LSTM 是否需要对 EEG 信号进行特征提取和特征选择？或者是否会自动从 EEG 信号中学习所需的特征？

回复
- Jason Brownlee 2021年2月17日上午5:27 #
  
  它可以学会从信号中提取特征。
  
  回复
Jessy 2021年2月24日下午7:46 #

嗨，杰森，
深度学习模型（LSTM）在使用 EEG 数据集时是否需要任何显式的特征选择和特征提取技术？

回复
- Jason Brownlee 2021年2月25日上午5:27 #
  
  这不一定。尝试有和没有这些技术，并比较模型在您的数据集上的性能。使用效果最好的。
  
  回复
Zainal 2021年10月6日下午6:20 #

尊敬的 Jason Brownlee 教授，感谢您的教程和解释。
我想问一下，我们是否可以使用这种权重正则化 LSTM 来进行分类？例如，就像本网站上找到的 HAR 一样。
如果是，步骤是否相同？
我仍然只是在学习 LSTM 和 python，所以如果我的问题太基础，我很抱歉。
非常感谢。

回复
- Adrian Tam 2021年10月7日上午2:58 #
  
  应该可以，但 LSTM 是为时间序列设计的，所以网络可以记住一些东西。这对于分类有用吗？您可以尝试确认。
  
  回复
José 2022年1月18日上午1:04 #

很棒的文章！！！

你能解释一下为什么你使用：X.reshape(X.shape[0], 1, X.shape[1]) 吗？

谢谢你

回复
- James Carmichael 2022年1月20日上午8:23 #
  
  你好 Jose… 请参考以下关于重塑输入数据的内容。
  
  https://machinelearning.org.cn/reshape-input-data-long-short-term-memory-networks-keras/
  
  回复
Akkis 2022年8月21日下午7:34 #

嘿！！我们可以用一个函数来修改 LSTM 的权重吗？
权重=f(x,y)
然后，将其分配给模型。

回复
- James Carmichael 2022年8月22日上午9:05 #
  
  你好 Akkis… 以下资源可能感兴趣。
  
  https://machinelearning.org.cn/update-lstm-networks-training-time-series-forecasting/
  
  回复
Andrea 2022年10月17日下午7:49 #

如何推断哪些权重（以及与哪些输入相关）被正则化了？

回复
- James Carmichael 2022年10月18日上午10:02 #
  
  你好 Andrea… 以下资源可能对您感兴趣。
  
  https://machinelearning.org.cn/weight-regularization-to-reduce-overfitting-of-deep-learning-models/
  
  回复

导航

LSTM 网络中的权重正则化用于时间序列预测

教程概述

环境

时间序列深度学习需要帮助吗？

洗发水销售数据集

实验测试框架

数据分割

模型评估

数据准备

LSTM 模型

实验运行

基线 LSTM 模型

偏置加权正则化

输入加权正则化

循环加权正则化

扩展

总结

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

最终将深度学习应用于您的时间序列预测项目

关于此主题的更多信息

65 条对使用 LSTM 网络进行时间序列预测的权重正则化的回复

留下回复点击此处取消回复。

导航

教程概述

环境

时间序列深度学习需要帮助吗？

洗发水销售数据集

实验测试框架

数据分割

模型评估

数据准备

LSTM 模型

实验运行

基线 LSTM 模型

偏置加权正则化

输入加权正则化

循环加权正则化

扩展

总结

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

最终将深度学习应用于您的时间序列预测项目

关于此主题的更多信息

65 条对使用 LSTM 网络进行时间序列预测的权重正则化的回复

留下回复 点击此处取消回复。

留下回复点击此处取消回复。