一个深度学习模型最简单的形式就是串联起来的感知机层。如果没有激活函数，它们就只是进行矩阵乘法，功能有限，无论有多少层。激活函数是神经网络能够近似各种非线性函数的神奇之处。在 PyTorch 中，有许多激活函数可供在深度学习模型中使用。在本博文中，您将看到激活函数的选择如何影响模型。具体来说：
- 什么是常见的激活函数
- 激活函数的性质是什么
- 不同的激活函数如何影响学习率
- 激活函数的选择如何解决梯度消失问题
通过我的《用PyTorch进行深度学习》一书来启动你的项目。它提供了包含可用代码的自学教程。
让我们开始吧。
在深度学习模型中使用激活函数
照片由 SHUJA OFFICIAL 拍摄。保留部分权利。
概述
这篇文章分为三个部分；它们是
- 二元分类的玩具模型
- 为什么需要非线性函数？
- 激活函数的效果
二元分类的玩具模型
让我们从一个简单的二元分类示例开始。在这里，您将使用 scikit-learn 的 `make_circle()` 函数为二元分类创建合成数据集。该数据集包含两个特征：点的 x 坐标和 y 坐标。每个点属于两个类别中的一个。您可以生成 1000 个数据点并按如下方式可视化它们：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
from sklearn.datasets import make_circles import matplotlib.pyplot as plt import torch import torch.nn as nn import torch.optim as optim # 制作数据：xy 平面上的两个圆圈作为分类问题 X, y = make_circles(n_samples=1000, factor=0.5, noise=0.1) X = torch.tensor(X, dtype=torch.float32) y = torch.tensor(y.reshape(-1, 1), dtype=torch.float32) plt.figure(figsize=(8,6)) plt.scatter(X[:,0], X[:,1], c=y) plt.show() |
数据集的可视化结果如下：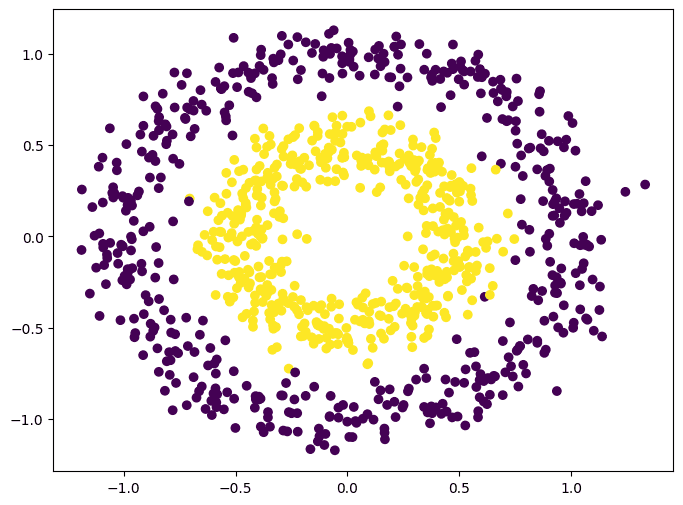
这个数据集很特别，因为它虽然简单但不是线性可分的：无法找到一条直线来分隔两个类别。神经网络如何找出类别之间存在圆形边界是一个挑战。
让我们为这个问题创建一个深度学习模型。为了简化起见，我们不进行交叉验证。您可能会发现神经网络过拟合了数据，但这不会影响下面的讨论。该模型有 4 个隐藏层，输出层为二元分类提供一个 sigmoid 值（0 到 1）。模型在其构造函数中接受一个参数来指定隐藏层中使用的激活函数。您将训练循环实现为一个函数，因为我们将多次运行它。
实现如下：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
class Model(nn.Module): def __init__(self, activation=nn.ReLU): super().__init__() self.layer0 = nn.Linear(2,5) self.act0 = activation() self.layer1 = nn.Linear(5,5) self.act1 = activation() self.layer2 = nn.Linear(5,5) self.act2 = activation() self.layer3 = nn.Linear(5,5) self.act3 = activation() self.layer4 = nn.Linear(5,1) self.act4 = nn.Sigmoid() def forward(self, x): x = self.act0(self.layer0(x)) x = self.act1(self.layer1(x)) x = self.act2(self.layer2(x)) x = self.act3(self.layer3(x)) x = self.act4(self.layer4(x)) return x def train_loop(model, X, y, n_epochs=300, batch_size=32): loss_fn = nn.BCELoss() optimizer = optim.Adam(model.parameters(), lr=0.0001) batch_start = torch.arange(0, len(X), batch_size) bce_hist = [] acc_hist = [] for epoch in range(n_epochs): # 使用优化器训练模型 model.train() for start in batch_start: X_batch = X[start:start+batch_size] y_batch = y[start:start+batch_size] y_pred = model(X_batch) loss = loss_fn(y_pred, y_batch) optimizer.zero_grad() loss.backward() optimizer.step() # 在每个 epoch 结束时评估 BCE 和准确率 model.eval() with torch.no_grad(): y_pred = model(X) bce = float(loss_fn(y_pred, y)) acc = float((y_pred.round() == y).float().mean()) bce_hist.append(bce) acc_hist.append(acc) # 每 10 个 epoch 打印一次指标 if (epoch+1) % 10 == 0: print("Epoch %d 之前：BCE=%.4f, Accuracy=%.2f%%" % (epoch+1, bce, acc*100)) return bce_hist, acc_hist |
在训练函数中，每个 epoch 结束时，我们使用整个数据集来评估模型。评估结果将在训练完成后返回。接下来，我们创建一个模型，对其进行训练，并绘制训练历史。我们使用的激活函数是**ReLU（Rectified Linear Unit）**，这是当今最常见的激活函数。
|
1 2 3 4 5 6 7 8 9 10 |
activation = nn.ReLU model = Model(activation=activation) bce_hist, acc_hist = train_loop(model, X, y) plt.plot(bce_hist, label="BCE") plt.plot(acc_hist, label="Accuracy") plt.xlabel("Epochs") plt.ylim(0, 1) plt.title(str(activation)) plt.legend() plt.show() |
运行这个代码会得到以下结果：
|
1 2 3 4 5 6 7 |
Epoch 10 之前：BCE=0.7025, Accuracy=50.00% Epoch 20 之前：BCE=0.6990, Accuracy=50.00% Epoch 30 之前：BCE=0.6959, Accuracy=50.00% ... Epoch 280 之前：BCE=0.3051, Accuracy=96.30% Epoch 290 之前：BCE=0.2785, Accuracy=96.90% Epoch 300 之前：BCE=0.2543, Accuracy=97.00% |
以及这个图：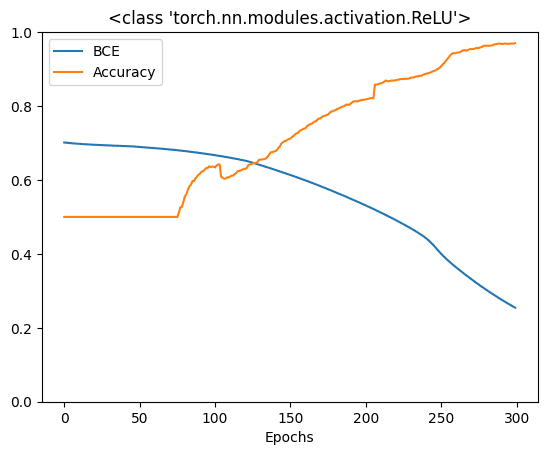
这个模型效果很好。在 300 个 epoch 后，它可以达到 90% 的准确率。然而，ReLU 并非唯一的激活函数。在历史上，sigmoid 函数和双曲正切函数在神经网络文献中很常见。如果您想了解更多，下面是您如何使用 matplotlib 比较这三个激活函数的方法：
|
1 2 3 4 5 6 7 8 9 10 11 |
x = torch.linspace(-4, 4, 200) relu = nn.ReLU()(x) tanh = nn.Tanh()(x) sigmoid = nn.Sigmoid()(x) plt.plot(x, sigmoid, label="sigmoid") plt.plot(x, tanh, label="tanh") plt.plot(x, relu, label="ReLU") plt.ylim(-1.5, 2) plt.legend() plt.show() |
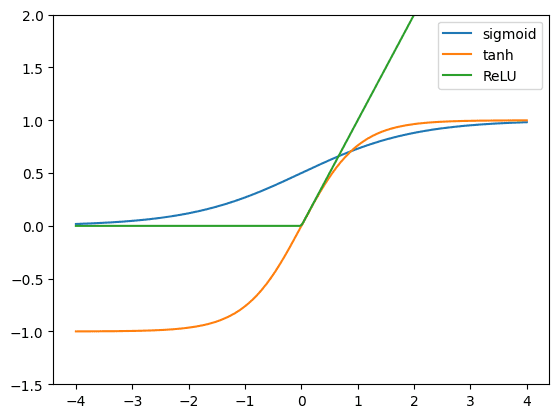
ReLU 被称为修正线性单元，因为它在 x 为正时是一个线性函数 $y=x$，而在 x 为负时保持为零。数学上，它是 $y=\max(0, x)$。双曲正切函数 ($y=\tanh(x)=\dfrac{e^x – e^{-x}}{e^x+e^{-x}}$) 平滑地从 -1 变化到 +1，而 sigmoid 函数 ($y=\sigma(x)=\dfrac{1}{1+e^{-x}}$) 从 0 变化到 +1。
如果您尝试对这些函数进行微分，您会发现 ReLU 最容易：在正区域的梯度是 1，否则为 0。双曲正切的斜率比 sigmoid 函数更大，因此其梯度也更大。
所有这些函数都是递增的。因此，它们的梯度永远不会是负数。这是激活函数适合在神经网络中使用的标准之一。
想开始使用PyTorch进行深度学习吗？
立即参加我的免费电子邮件速成课程（附示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
为什么需要非线性函数？
您可能想知道，为什么所有这些关于非线性激活函数的炒作？或者为什么我们不能在使用前一层激活的加权线性组合之后使用一个恒等函数？使用多个线性层基本上等同于使用一个线性层。这可以通过一个简单的例子来说明。假设您有一个单隐藏层神经网络，每个隐藏层有两个神经元。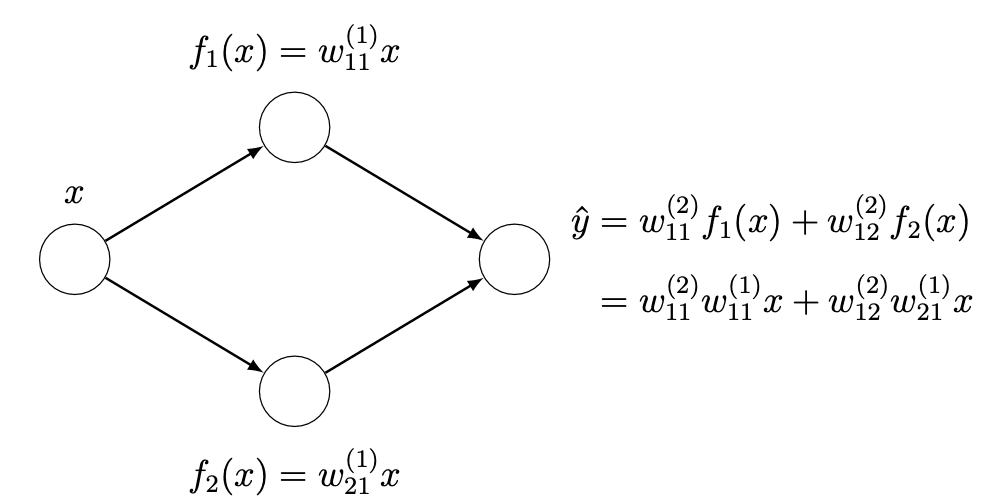
如果您使用一个线性隐藏层，您可以将输出层重写为原始输入变量的线性组合。如果您有更多的神经元和权重，方程会更长，具有更多的嵌套和连续层权重之间的更多乘法。然而，原理是相同的：您可以将整个网络表示为一个单一的线性层。为了让网络表示更复杂的函数，您需要非线性激活函数。
激活函数的效果
为了说明激活函数能给您的模型带来多大的影响，让我们修改训练循环函数来捕获更多数据：即每个训练步骤中的梯度。您的模型有四个隐藏层和一个输出层。在每个步骤中，反向传播计算每个层的权重的梯度，并且权重更新由优化器根据反向传播的结果完成。您应该观察到梯度如何在训练过程中发生变化。因此，训练循环函数被修改为收集每个步骤中每个层的梯度的平均绝对值，如下所示：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
def train_loop(model, X, y, n_epochs=300, batch_size=32): loss_fn = nn.BCELoss() optimizer = optim.Adam(model.parameters(), lr=0.0001) batch_start = torch.arange(0, len(X), batch_size) bce_hist = [] acc_hist = [] grad_hist = [[],[],[],[],[]] for epoch in range(n_epochs): # 使用优化器训练模型 model.train() layer_grad = [[],[],[],[],[]] for start in batch_start: X_batch = X[start:start+batch_size] y_batch = y[start:start+batch_size] y_pred = model(X_batch) loss = loss_fn(y_pred, y_batch) optimizer.zero_grad() loss.backward() optimizer.step() # 收集梯度的平均绝对值 layers = [model.layer0, model.layer1, model.layer2, model.layer3, model.layer4] for n,layer in enumerate(layers): mean_grad = float(layer.weight.grad.abs().mean()) layer_grad[n].append(mean_grad) # 在每个 epoch 结束时评估 BCE 和准确率 model.eval() with torch.no_grad(): y_pred = model(X) bce = float(loss_fn(y_pred, y)) acc = float((y_pred.round() == y).float().mean()) bce_hist.append(bce) acc_hist.append(acc) for n, grads in enumerate(layer_grad): grad_hist[n].append(sum(grads)/len(grads)) # 每 10 个 epoch 打印一次指标 if epoch % 10 == 9: print("Epoch %d: BCE=%.4f, Accuracy=%.2f%%" % (epoch, bce, acc*100)) return bce_hist, acc_hist, layer_grad |
在内部 for 循环结束时，层权重的梯度是通过之前的反向传播计算的，您可以通过 model.layer0.weight.grad 访问梯度。与权重一样，梯度也是张量。您取每个元素的绝对值，然后计算所有元素的平均值。此值取决于批次，并且可能非常嘈杂。因此，您在最后汇总每个 epoch 中所有此类平均绝对值。
请注意，神经网络中有五个层（隐藏层和输出层合并）。因此，如果您可视化它们，可以看到每个层梯度随 epoch 的变化模式。下面，您将像以前一样运行训练循环，并绘制交叉熵和准确率以及每个层的平均绝对梯度。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
activation = nn.ReLU model = Model(activation=activation) bce_hist, acc_hist, grad_hist = train_loop(model, X, y) fig, ax = plt.subplots(1, 2, figsize=(12, 5)) ax[0].plot(bce_hist, label="BCE") ax[0].plot(acc_hist, label="Accuracy") ax[0].set_xlabel("Epochs") ax[0].set_ylim(0, 1) for n, grads in enumerate(grad_hist): ax[1].plot(grads, label="layer"+str(n)) ax[1].set_xlabel("Epochs") fig.suptitle(str(activation)) ax[0].legend() ax[1].legend() plt.show() |
运行上面的代码会产生以下图表
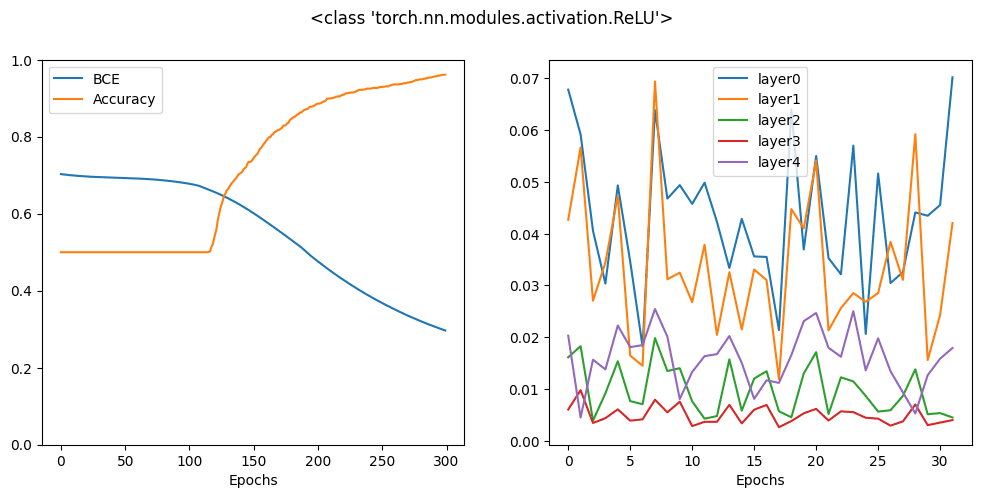
在上面的图中，您可以看到准确率如何提高，交叉熵损失如何降低。同时，您可以看到每个层的梯度都在相似的范围内波动，特别是您应该关注对应于第一层和最后一层的线条。这种行为是理想的。
让我们用 sigmoid 激活函数重复同样的操作
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
activation = nn.Sigmoid model = Model(activation=activation) bce_hist, acc_hist, grad_hist = train_loop(model, X, y) fig, ax = plt.subplots(1, 2, figsize=(12, 5)) ax[0].plot(bce_hist, label="BCE") ax[0].plot(acc_hist, label="Accuracy") ax[0].set_xlabel("Epochs") ax[0].set_ylim(0, 1) for n, grads in enumerate(grad_hist): ax[1].plot(grads, label="layer"+str(n)) ax[1].set_xlabel("Epochs") fig.suptitle(str(activation)) ax[0].legend() ax[1].legend() plt.show() |
其图表如下：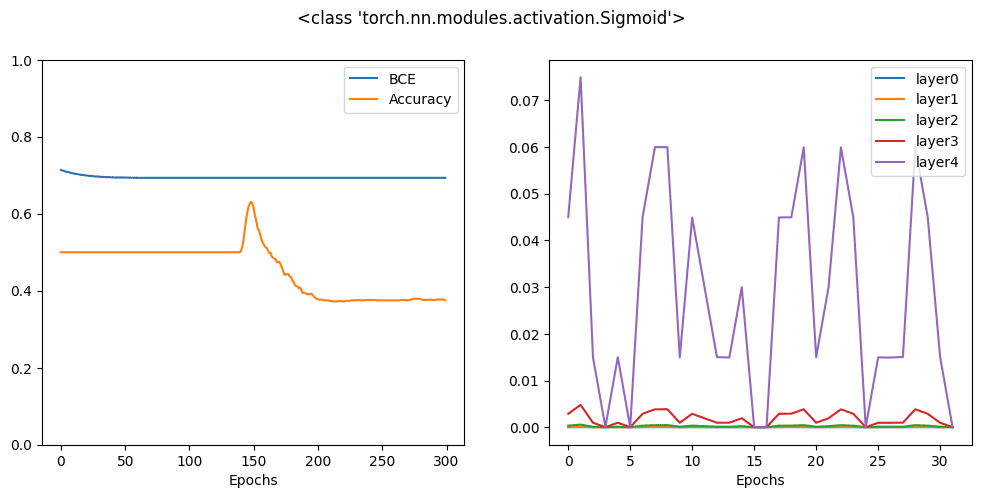
您可以看到，经过 300 个 epoch 后，最终结果比 ReLU 激活函数差得多。实际上，您可能需要更多 epoch 才能使此模型收敛。原因很容易从右侧的图表中找到，您可以看到梯度仅在输出层显着，而所有隐藏层的梯度几乎为零。这就是**梯度消失效应**，这是许多带有 sigmoid 激活函数的神经网络模型的常见问题。
双曲正切函数具有与 sigmoid 函数相似的形状，但其曲线更陡峭。让我们看看它的行为。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
activation = nn.Tanh model = Model(activation=activation) bce_hist, acc_hist, grad_hist = train_loop(model, X, y) fig, ax = plt.subplots(1, 2, figsize=(12, 5)) ax[0].plot(bce_hist, label="BCE") ax[0].plot(acc_hist, label="Accuracy") ax[0].set_xlabel("Epochs") ax[0].set_ylim(0, 1) for n, grads in enumerate(grad_hist): ax[1].plot(grads, label="layer"+str(n)) ax[1].set_xlabel("Epochs") fig.suptitle(str(activation)) ax[0].legend() ax[1].legend() plt.show() |
结果是：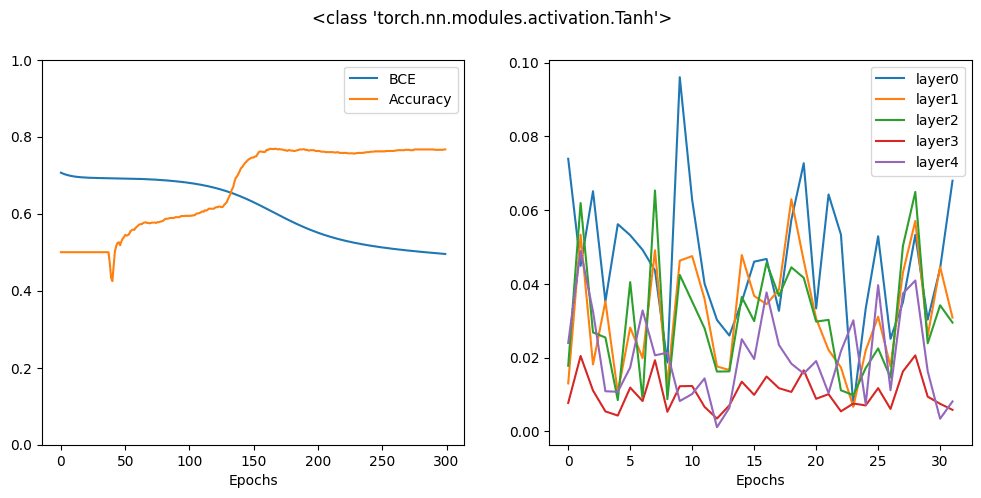
结果看起来比 sigmoid 激活函数好，但仍然比 ReLU 差。事实上，从梯度图来看，您可以注意到隐藏层的梯度是显着的，但第一隐藏层的梯度明显比输出层的梯度小一个数量级。因此，反向传播在将梯度传播到输入方面效果不佳。
这就是为什么如今的每个神经网络模型都会使用 ReLU 激活函数的原因。不仅因为 ReLU 更简单，其微分计算比其他激活函数更快，而且因为它能使模型更快地收敛。
事实上，您有时可以做得比 ReLU 更好。在 PyTorch 中，有许多 ReLU 变体。让我们看一下其中的两个。您可以如下比较这三种 ReLU 变体：
|
1 2 3 4 5 6 7 8 9 10 |
x = torch.linspace(-8, 8, 200) relu = nn.ReLU()(x) relu6 = nn.ReLU6()(x) leaky = nn.LeakyReLU()(x) plt.plot(x, relu, label="ReLU") plt.plot(x, relu6, label="ReLU6") plt.plot(x, leaky, label="LeakyReLU") plt.legend() plt.show() |
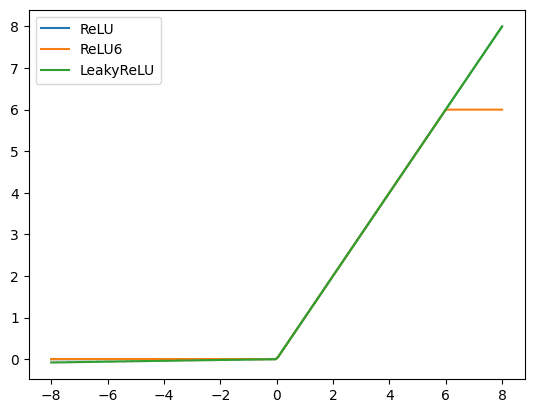首先是 ReLU6，它是一个 ReLU 函数，但如果函数的输入大于 6.0，则将其限制在 6.0。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
activation = nn.ReLU6 model = Model(activation=activation) bce_hist, acc_hist, grad_hist = train_loop(model, X, y) fig, ax = plt.subplots(1, 2, figsize=(12, 5)) ax[0].plot(bce_hist, label="BCE") ax[0].plot(acc_hist, label="Accuracy") ax[0].set_xlabel("Epochs") ax[0].set_ylim(0, 1) for n, grads in enumerate(grad_hist): ax[1].plot(grads, label="layer"+str(n)) ax[1].set_xlabel("Epochs") fig.suptitle(str(activation)) ax[0].legend() ax[1].legend() plt.show() |
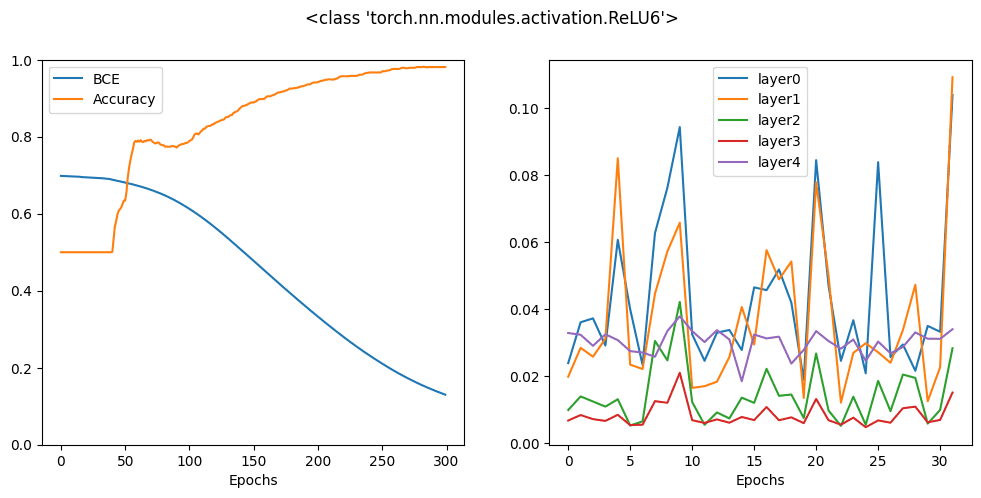接下来是 leaky ReLU，ReLU 的负半部分不再是平坦的，而是呈缓坡直线。其原理是在此区域保持小的正梯度。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
activation = nn.LeakyReLU model = Model(activation=activation) bce_hist, acc_hist, grad_hist = train_loop(model, X, y) fig, ax = plt.subplots(1, 2, figsize=(12, 5)) ax[0].plot(bce_hist, label="BCE") ax[0].plot(acc_hist, label="Accuracy") ax[0].set_xlabel("Epochs") ax[0].set_ylim(0, 1) for n, grads in enumerate(grad_hist): ax[1].plot(grads, label="layer"+str(n)) ax[1].set_xlabel("Epochs") fig.suptitle(str(activation)) ax[0].legend() ax[1].legend() plt.show() |
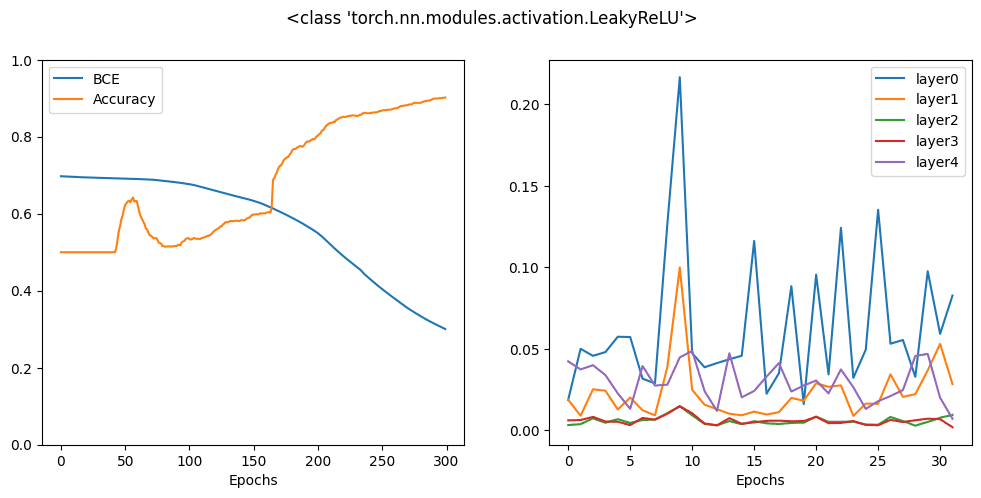
您可以看到，所有这些变体在 300 个 epoch 后都可以提供相似的准确率，但从历史曲线可以看出，有些变体比其他变体更快地达到高准确率。这是因为激活函数的梯度与优化器之间存在交互。没有一个激活函数是万能的，但设计是有帮助的
- 在反向传播中，将损失指标从输出层一直传递到输入层。
- 在特定条件下（例如，限制浮点精度）保持稳定的梯度计算。
- 对不同输入提供足够的对比度，以便反向传播能够确定对参数的准确调整。
以下是生成上述所有图表的完整代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
from sklearn.datasets import make_circles import matplotlib.pyplot as plt import torch import torch.nn as nn import torch.optim as optim # 制作数据：xy 平面上的两个圆圈作为分类问题 X, y = make_circles(n_samples=1000, factor=0.5, noise=0.1) X = torch.tensor(X, dtype=torch.float32) y = torch.tensor(y.reshape(-1, 1), dtype=torch.float32) # 二分类模型 class Model(nn.Module): def __init__(self, activation=nn.ReLU): super().__init__() self.layer0 = nn.Linear(2,5) self.act0 = activation() self.layer1 = nn.Linear(5,5) self.act1 = activation() self.layer2 = nn.Linear(5,5) self.act2 = activation() self.layer3 = nn.Linear(5,5) self.act3 = activation() self.layer4 = nn.Linear(5,1) self.act4 = nn.Sigmoid() def forward(self, x): x = self.act0(self.layer0(x)) x = self.act1(self.layer1(x)) x = self.act2(self.layer2(x)) x = self.act3(self.layer3(x)) x = self.act4(self.layer4(x)) return x # 训练模型并生成历史记录 def train_loop(model, X, y, n_epochs=300, batch_size=32): loss_fn = nn.BCELoss() optimizer = optim.Adam(model.parameters(), lr=0.0001) batch_start = torch.arange(0, len(X), batch_size) bce_hist = [] acc_hist = [] grad_hist = [[],[],[],[],[]] for epoch in range(n_epochs): # 使用优化器训练模型 model.train() layer_grad = [[],[],[],[],[]] for start in batch_start: X_batch = X[start:start+batch_size] y_batch = y[start:start+batch_size] y_pred = model(X_batch) loss = loss_fn(y_pred, y_batch) optimizer.zero_grad() loss.backward() optimizer.step() # 收集梯度的平均绝对值 layers = [model.layer0, model.layer1, model.layer2, model.layer3, model.layer4] for n,layer in enumerate(layers): mean_grad = float(layer.weight.grad.abs().mean()) layer_grad[n].append(mean_grad) # 在每个 epoch 结束时评估 BCE 和准确率 model.eval() with torch.no_grad(): y_pred = model(X) bce = float(loss_fn(y_pred, y)) acc = float((y_pred.round() == y).float().mean()) bce_hist.append(bce) acc_hist.append(acc) for n, grads in enumerate(layer_grad): grad_hist[n].append(sum(grads)/len(grads)) # 每 10 个 epoch 打印一次指标 if epoch % 10 == 9: print("Epoch %d: BCE=%.4f, Accuracy=%.2f%%" % (epoch, bce, acc*100)) return bce_hist, acc_hist, layer_grad # 选择不同的激活函数并直观地比较结果 for activation in [nn.Sigmoid, nn.Tanh, nn.ReLU, nn.ReLU6, nn.LeakyReLU]: model = Model(activation=activation) bce_hist, acc_hist, grad_hist = train_loop(model, X, y) fig, ax = plt.subplots(1, 2, figsize=(12, 5)) ax[0].plot(bce_hist, label="BCE") ax[0].plot(acc_hist, label="Accuracy") ax[0].set_xlabel("Epochs") ax[0].set_ylim(0, 1) for n, grads in enumerate(grad_hist): ax[1].plot(grads, label="layer"+str(n)) ax[1].set_xlabel("Epochs") fig.suptitle(str(activation)) ax[0].legend() ax[1].legend() plt.show() |
进一步阅读
如果您想深入了解，本节提供了更多关于该主题的资源。
- PyTorch 文档中的 nn.Sigmoid
- PyTorch 文档中的 nn.Tanh
- PyTorch 文档中的 nn.ReLU
- PyTorch 文档中的 nn.ReLU6
- PyTorch 文档中的 nn.LeakyReLU
- 梯度消失问题, Wikipedia
总结
在本章中，您将学习如何为 PyTorch 模型选择激活函数。您将了解：
- 常见的激活函数及其外观。
- 如何在 PyTorch 模型中使用激活函数。
- 什么是梯度消失问题。
- 激活函数对模型性能的影响。
开始使用PyTorch进行深度学习！
学习如何构建深度学习模型
...使用新发布的PyTorch 2.0库
在我的新电子书中探索如何实现
使用 PyTorch进行深度学习
它提供了包含数百个可用代码的自学教程，让你从新手变成专家。它将使你掌握：
张量操作、训练、评估、超参数优化等等...
你好，
这是一个非常有用的教程，非常感谢！
但这 2 个陈述对我来说不清楚，你能进一步解释一下吗？
1) 在反向传播中，将损失指标从输出层一直传递到输入层。
2) 在特定条件下（例如，限制浮点精度）保持稳定的梯度计算。
你好 Evren……不客气！以下资源可能对您有帮助：
https://machinelearning.org.cn/implement-backpropagation-algorithm-scratch-python/