激活函数在神经网络中起着至关重要的作用,它们通过引入非线性来增强模型的表达能力。这种非线性使得神经网络能够根据输入开发复杂的表示和函数,而这对于简单的线性回归模型来说是不可能实现的。
在神经网络的历史上,人们提出了许多不同的非线性激活函数。在本文中,您将探讨三种流行的激活函数:Sigmoid、Tanh 和 ReLU。
阅读本文后,您将了解到:
- 为什么非线性在神经网络中很重要
- 不同的激活函数如何导致梯度消失问题
- Sigmoid、Tanh 和 ReLU 激活函数
- 如何在 TensorFlow 模型中使用不同的激活函数
让我们开始吧。

在 TensorFlow 中使用激活函数
照片由 Victor Freitas 拍摄。部分权利保留。
概述
本文分为五个部分:
- 为什么我们需要非线性激活函数
- Sigmoid 函数和梯度消失
- 双曲正切函数
- ReLU(Rectified Linear Unit)
- 在实践中使用激活函数
为什么我们需要非线性激活函数
您可能会想,为什么人们对非线性激活函数如此热衷?或者为什么我们不能在上一层神经元的加权线性组合后直接使用恒等函数?使用多个线性层实际上等同于使用一个线性层。这可以通过一个简单的例子来说明。
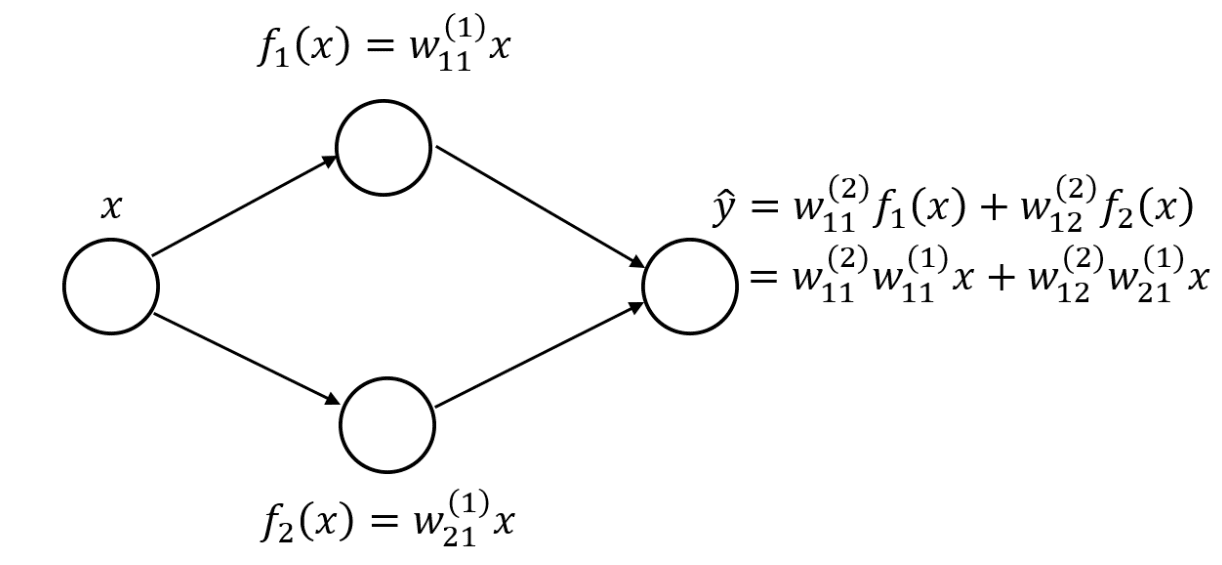
假设您有一个单隐藏层神经网络,每个隐藏层有两个神经元。
如果您使用了线性隐藏层,您可以将输出层重写为原始输入变量的线性组合。如果您有更多的神经元和权重,方程会更长,嵌套更多,并且连续层权重之间的乘法更多。但是,其原理是相同的:您可以将整个网络表示为一个单一的线性层。
为了让网络表示更复杂的函数,您需要非线性激活函数。让我们从一个流行的例子开始,即 Sigmoid 函数。
Sigmoid 函数与梯度消失
Sigmoid 激活函数是神经网络中非线性激活函数的流行选择。它流行的原因之一是它的输出值在 0 和 1 之间,这可以模拟概率值。因此,它用于将线性层的实值输出转换为概率,该概率可用作概率输出。这使其成为逻辑回归方法的重要组成部分,逻辑回归方法可直接用于二分类。
Sigmoid 函数通常用 $\sigma$ 表示,其形式为 $\sigma = \frac{1}{1 + e^{-1}}$。在 TensorFlow 中,您可以从 Keras 库调用 Sigmoid 函数,如下所示:
|
1 2 3 4 5 |
import tensorflow as tf from tensorflow.keras.activations import sigmoid input_array = tf.constant([-1, 0, 1], dtype=tf.float32) print (sigmoid(input_array)) |
这将产生以下输出:
|
1 |
tf.Tensor([0.26894143 0.5 0.7310586 ], shape=(3,), dtype=float32) |
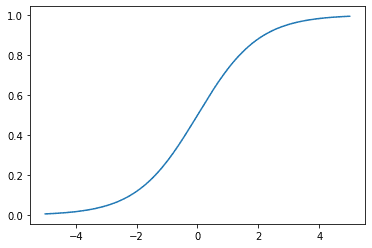
您也可以将 Sigmoid 函数绘制为 $x$ 的函数,
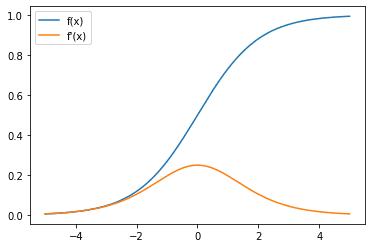
在查看神经网络中神经元的激活函数时,您还应该关注其导数,因为反向传播和链式法则会影响神经网络如何从数据中学习。
在这里,您可以观察到 Sigmoid 函数的梯度始终在 0 和 0.25 之间。并且当 $x$ 趋向于正无穷大或负无穷大时,梯度趋向于零。这可能会导致梯度消失问题,即当输入具有较大的 $x$ 幅度时(例如,由于早期层的输出),梯度太小而无法启动校正。
梯度消失是一个问题,因为链式法则用于深度神经网络中的反向传播。 回想一下,在神经网络中,每个层的梯度(损失函数)是其后续层的梯度乘以其激活函数的梯度。由于网络中有很多层,如果激活函数的梯度小于 1,那么远离输出层的某个层的梯度将接近于零。任何梯度接近于零的层都会阻止梯度进一步传播到早期层。
由于 Sigmoid 函数的值始终小于 1,具有更多层的网络会加剧梯度消失问题。此外,还存在一个饱和区域,在该区域中,Sigmoid 的梯度趋向于 0,即当输入 $x$ 的幅度增大时。因此,如果来自先前层的加权激活和的输出很大,那么由于激活函数相对于激活函数输入的导数很小(在饱和区域),通过该神经元的梯度将非常小。
当然,还有前一层激活与线性项的导数,因为权重可能很大,并且它是来自不同神经元的导数的总和,所以该层的导数可能大于 1。然而,在训练开始时,这可能仍然令人担忧,因为权重通常被初始化为较小的值。
双曲正切函数
另一个需要考虑的激活函数是 tanh 激活函数,也称为双曲正切函数。与 Sigmoid 函数相比,它具有更大的输出值范围和更大的最大梯度。Tanh 函数是普通切线函数相对于圆的“双曲类比”,大多数人对此都很熟悉。
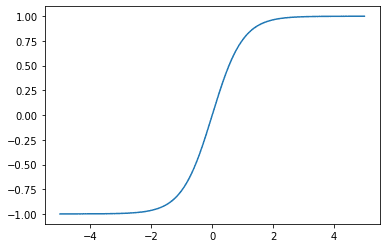
绘制 tanh 函数
让我们也看看它的梯度
请注意,与 Sigmoid 函数(最大梯度值为 0.25)相比,这里的梯度最大值为 1。这使得具有 Tanh 激活的神经网络不太容易出现梯度消失问题。但是,Tanh 函数也有一个饱和区域,当输入 $x$ 的幅度增大时,该区域的梯度值趋向于零。
在 TensorFlow 中,您可以使用 Keras 激活模块中的 `tanh` 函数在张量上实现 Tanh 激活。
|
1 2 3 4 5 |
import tensorflow as tf from tensorflow.keras.activations import tanh input_array = tf.constant([-1, 0, 1], dtype=tf.float32) print (tanh(input_array)) |
这将产生以下输出:
|
1 |
tf.Tensor([-0.7615942 0. 0.7615942], shape=(3,), dtype=float32) |
ReLU(Rectified Linear Unit)
最后一个详细介绍的激活函数是 ReLU(Rectified Linear Unit),也称为 ReLU。它最近因其相对简单的计算而变得流行。这有助于加速神经网络,并且能获得良好的经验性能,使其成为激活函数的不错首选。
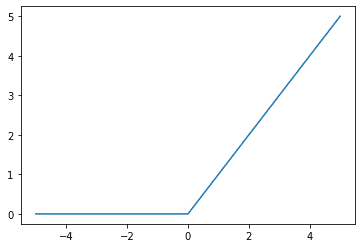
ReLU 函数是一个简单的 $\max(0, x)$ 函数,它也可以看作是一个分段函数,其中所有小于 0 的输入映射到 0,所有大于或等于 0 的输入映射回自身(即,恒等函数)。图示如下:
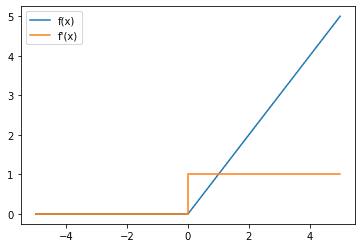
接下来,您还可以查看 ReLU 函数的梯度:
请注意,当输入为正时,ReLU 的梯度为 1,这有助于解决梯度消失问题。但是,当输入为负时,梯度为 0。这可能会导致另一个问题,即“死神经元”或“僵尸 ReLU”问题,如果神经元被**持续禁用**,则会出现此问题。
在这种情况下,由于链式法则作为其一项,神经元将始终具有 0 梯度,因此无法学习,并且其权重也永远不会被更新。如果这种情况发生在您的数据集中的所有数据上,那么除非前一层的激活发生变化,使得神经元不再“死亡”,否则该神经元很难从您的数据集中学习。
在 TensorFlow 中使用 ReLU 激活:
|
1 2 3 4 5 |
import tensorflow as tf from tensorflow.keras.activations import relu input_array = tf.constant([-1, 0, 1], dtype=tf.float32) print (relu(input_array)) |
这将产生以下输出:
|
1 |
tf.Tensor([0. 0. 1.], shape=(3,), dtype=float32) |
上面回顾的三种激活函数都表明它们是单调递增函数。这是必需的;否则,您将无法应用梯度下降算法。
既然您已经探索了一些常见的激活函数以及如何在 TensorFlow 中使用它们。让我们看看如何在实际模型中使用它们。
在实践中使用激活函数
在探索激活函数在实践中的应用之前,让我们看看在将激活函数与其他 Keras 层结合使用时的一种常见方式。假设您想在 Dense 层之上添加 ReLU 激活。按照上面展示的方法,一种方法是这样做:
|
1 2 |
x = Dense(units=10)(input_layer) x = relu(x) |
但是,对于许多 Keras 层,您还可以使用更简洁的表示方法将激活添加到层之上:
|
1 |
x = Dense(units=10, activation=”relu”)(input_layer) |
使用这种更简洁的表示方法,让我们使用 Keras 构建我们的 LeNet5 模型:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
import tensorflow as tf import tensorflow.keras as keras from tensorflow.keras.layers import Dense, Input, Flatten, Conv2D, BatchNormalization, MaxPool2D from tensorflow.keras.models import Model (trainX, trainY), (testX, testY) = keras.datasets.cifar10.load_data() input_layer = Input(shape=(32,32,3,)) x = Conv2D(filters=6, kernel_size=(5,5), padding="same", activation="relu")(input_layer) x = MaxPool2D(pool_size=(2,2))(x) x = Conv2D(filters=16, kernel_size=(5,5), padding="same", activation="relu")(x) x = MaxPool2D(pool_size=(2, 2))(x) x = Conv2D(filters=120, kernel_size=(5,5), padding="same", activation="relu")(x) x = Flatten()(x) x = Dense(units=84, activation="relu")(x) x = Dense(units=10, activation="softmax")(x) model = Model(inputs=input_layer, outputs=x) print(model.summary()) model.compile(optimizer="adam", loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics="acc") history = model.fit(x=trainX, y=trainY, batch_size=256, epochs=10, validation_data=(testX, testY)) |
运行此代码将产生以下输出:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
Model: "model" _________________________________________________________________ 层 (类型) 输出形状 参数数量 ================================================================= input_1 (InputLayer) [(None, 32, 32, 3)] 0 conv2d (Conv2D) (None, 32, 32, 6) 456 max_pooling2d (MaxPooling2D (None, 16, 16, 6) 0 ) conv2d_1 (Conv2D) (None, 16, 16, 16) 2416 max_pooling2d_1 (MaxPooling (None, 8, 8, 16) 0 2D) conv2d_2 (Conv2D) (None, 8, 8, 120) 48120 flatten (Flatten) (None, 7680) 0 dense (Dense) (None, 84) 645204 dense_1 (Dense) (None, 10) 850 ================================================================= 总参数:697,046 可训练参数:697,046 不可训练参数: 0 _________________________________________________________________ 无 第 1/10 纪元 196/196 [==============================] - 14s 11ms/step - loss: 2.9758 acc: 0.3390 - val_loss: 1.5530 - val_acc: 0.4513 第 2/10 纪元 196/196 [==============================] - 2s 8ms/step - loss: 1.4319 - acc: 0.4927 - val_loss: 1.3814 - val_acc: 0.5106 第 3/10 纪元 196/196 [==============================] - 2s 8ms/step - loss: 1.2505 - acc: 0.5583 - val_loss: 1.3595 - val_acc: 0.5170 第 4/10 纪元 196/196 [==============================] - 2s 8ms/step - loss: 1.1127 - acc: 0.6094 - val_loss: 1.2892 - val_acc: 0.5534 第 5/10 纪元 196/196 [==============================] - 2s 8ms/step - loss: 0.9763 - acc: 0.6594 - val_loss: 1.3228 - val_acc: 0.5513 第 6/10 纪元 196/196 [==============================] - 2s 8ms/step - loss: 0.8510 - acc: 0.7017 - val_loss: 1.3953 - val_acc: 0.5494 第 7/10 纪元 196/196 [==============================] - 2s 8ms/step - loss: 0.7361 - acc: 0.7426 - val_loss: 1.4123 - val_acc: 0.5488 第 8/10 纪元 196/196 [==============================] - 2s 8ms/step - loss: 0.6060 - acc: 0.7894 - val_loss: 1.5356 - val_acc: 0.5435 第 9/10 纪元 196/196 [==============================] - 2s 8ms/step - loss: 0.5020 - acc: 0.8265 - val_loss: 1.7801 - val_acc: 0.5333 第 10/10 纪元 196/196 [==============================] - 2s 8ms/step - loss: 0.4013 - acc: 0.8605 - val_loss: 1.8308 - val_acc: 0.5417 |
这样,您就可以在 TensorFlow 模型中使用不同的激活函数了!
进一步阅读
其他激活函数示例
- Leaky ReLU(ReLU 的负斜率为非零): https://tensorflowcn.cn/api_docs/python/tf/keras/layers/LeakyReLU
- Parametric ReLU(负斜率为可学习参数): https://arxiv.org/abs/1502.01852
- Maxout Unit: https://arxiv.org/abs/1302.4389
总结
在本篇博文中,您已经了解了激活函数对于实现当今深度学习中常见的复杂神经网络的重要性。您还了解了一些流行的激活函数、它们的导数以及如何将它们集成到您的 TensorFlow 模型中。
具体来说,你学到了:
- 为什么非线性在神经网络中很重要
- 不同的激活函数如何导致梯度消失问题
- Sigmoid、Tanh 和 ReLU 激活函数
- 如何在 TensorFlow 模型中使用不同的激活函数





我很高兴看到我们又回到了 masterymachinelearning 上写代码了:)
感谢 Razvan 的反馈!
谢谢
不客气,s kARTHIK!
在 tanh 激活函数的示例中——假设您希望在输出层使用它,然后修改输出范围。您肯定可以编写自己的激活函数,但我很困惑如何在使用模型时提供这些限制作为参数,而不是硬编码它们。