在客户细分中使用机器学习

作者： Jayita Gulati 发布于 2024年7月20日分类：数据科学 2

Using Machine Learning in Customer Segmentation

图片来源：编辑 | Midjourney

过去，企业根据年龄或性别等简单因素对客户进行分组。现在，机器学习改变了这一过程。机器学习算法可以分析大量数据。在本文中，我们将探讨机器学习如何改进客户细分。

客户细分简介

客户细分将客户划分为不同的群体。这些群体基于相似的特征或行为。主要目标是更好地了解每个群体。这有助于企业制定适合每个群体特定需求的营销策略和产品。

客户可以根据以下几个标准进行分组：

人口统计细分：基于年龄、性别和职业等因素。
心理学细分：关注客户的生活方式和兴趣。
行为细分：分析客户行为，如品牌忠诚度和使用频率。
地理细分：根据客户的地理位置进行划分。

客户细分为企业提供了多种优势：

个性化营销：企业可以针对不同客户群体发送特定的信息。
提高客户留存率：组织可以识别客户偏好，使他们成为忠实客户。
增强产品开发：细分有助于了解客户需要什么样的产品。

用于客户细分的机器学习算法

机器学习使用多种算法根据客户的特征进行分类。一些常用的算法包括：

K-均值聚类：根据相似特征将客户划分为簇。
层次聚类：将客户组织成树状的簇层次结构。
DBSCAN：根据数据空间中点的密度识别簇。
主成分分析（PCA）：降低数据的维度并保留重要信息。
决策树：根据一系列分层决策对客户进行划分。
神经网络：通过相互连接的节点层学习数据中的复杂模式。

我们将使用 K-均值算法将客户细分为不同的群体。

K-均值聚类算法的实现

K-均值聚类是一种无监督算法。它在没有任何预定义标签或训练示例的情况下运行。该算法用于将数据集中的相似数据点分组。目标是将数据划分为多个簇。每个簇包含相似的数据点。让我们看看这个算法是如何工作的。

初始化：选择簇的数量 (k)。随机初始化 k 个点作为质心。
分配：将每个数据点分配给最近的质心，并形成簇。
更新质心：计算分配给每个质心的所有数据点的平均值。将质心移动到此平均位置。

重复步骤 2 和 3 直到收敛。

在接下来的章节中，我们将实现 K-均值聚类算法，根据不同特征将客户分组。

数据准备

让我们探索客户数据集。我们的数据集大约有 500,000 个数据点。

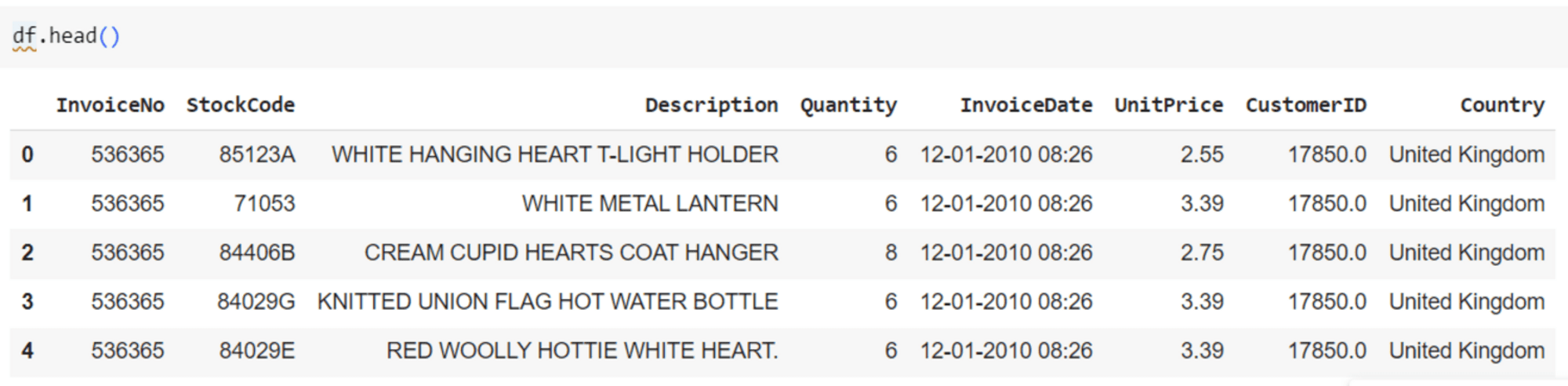
客户数据集

已移除缺失值和重复项，并选择三个特征（'Quantity'、'UnitPrice'、'CustomerID'）进行聚类。

import pandas as pd
from sklearn.preprocessing import StandardScaler

# Load the dataset (replace 'data.csv' with your actual file path)
df = pd.read_csv('userdata.csv')

# Data cleaning: remove duplicates and handle missing values
df = df.drop_duplicates()
df = df.dropna()

# Feature selection: selecting relevant features for clustering
selected_features = ['Quantity', 'UnitPrice', 'CustomerID']
X = df[selected_features]

# Normalization (standardization)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

import pandas as pd

from sklearn.preprocessing import StandardScaler

# 加载数据集（将“data.csv”替换为您的实际文件路径）

df = pd.read_csv('userdata.csv')

# 数据清洗：删除重复项并处理缺失值

df = df.drop_duplicates()

df = df.dropna()

# 特征选择：选择用于聚类的相关特征

selected_features = ['Quantity', 'UnitPrice', 'CustomerID']

X = df[selected_features]

# 归一化（标准化）

scaler = StandardScaler()

X_scaled = scaler.fit_transform(X)

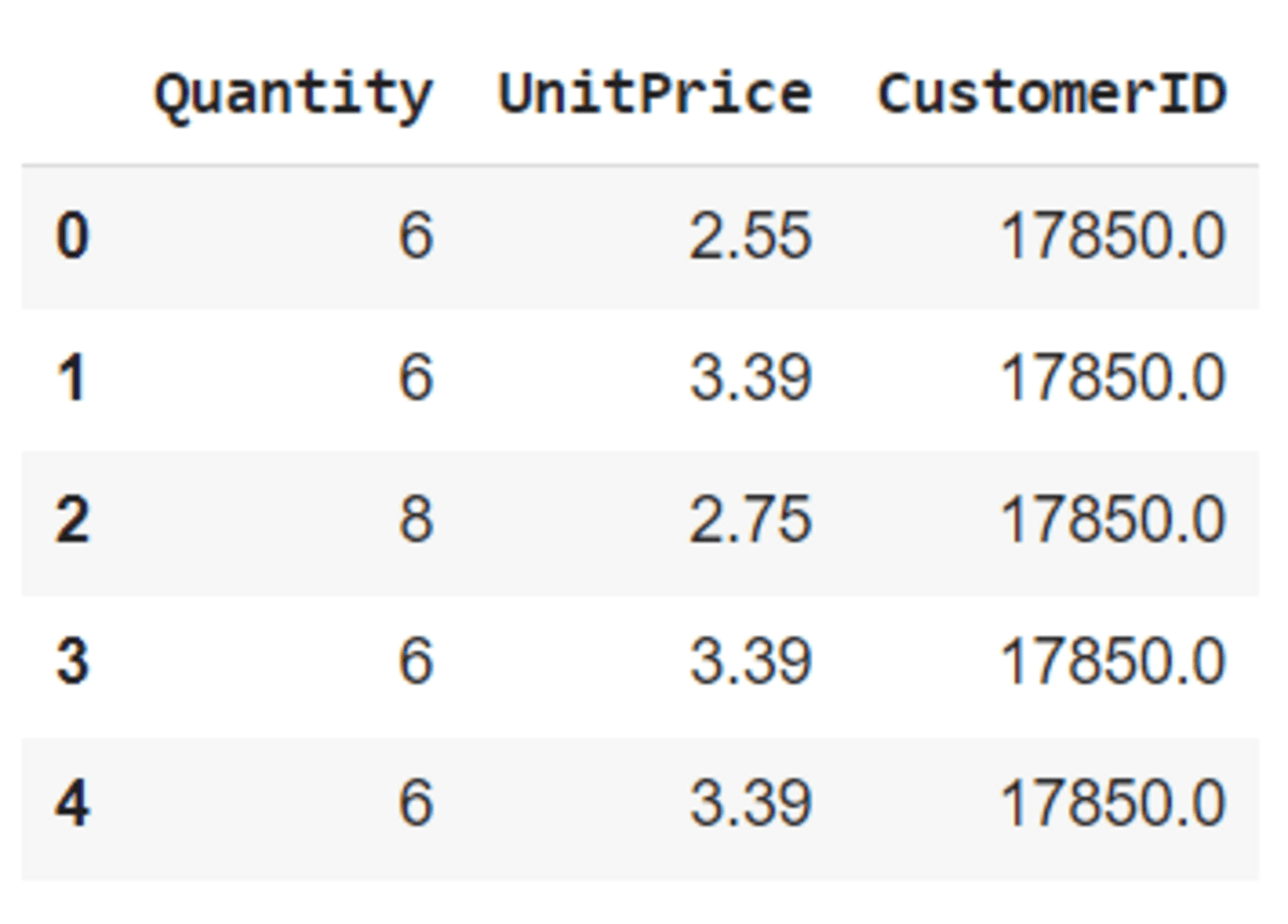
预处理数据集

超参数调优

K-均值聚类的一个挑战是找出最佳的簇数量。肘部法则可以帮助我们做到这一点。它绘制了每个点到其分配的簇质心的平方距离之和（惯性）与 K 的关系图。寻找惯性不再随 K 增加而显著减小的点。这个点被称为聚类模型的“肘部”。它建议了一个合适的 K 值。

# Determine the optimal number of clusters using the Elbow Method
def determine_optimal_clusters(X_scaled, max_clusters=10):
    distances = []

    for n in range(2, max_clusters+1):
        kmeans = KMeans(n_clusters=n, random_state=42)
        kmeans.fit(X_scaled)
        distances.append(kmeans.inertia_)

    plt.figure(figsize=(7, 5))
    plt.plot(range(2, max_clusters+1), distances, marker='o')
    plt.title('Elbow Method')
    plt.xlabel('Number of clusters')
    plt.ylabel('Sum of squared distances')
    plt.xticks(range(2, max_clusters+1))
    plt.grid(True)
    plt.show()

    return distances

distances = determine_optimal_clusters(X_scaled)

# 使用肘部法则确定最佳簇数

def determine_optimal_clusters(X_scaled, max_clusters=10):

distances = []

for n in range(2, max_clusters+1):

kmeans = KMeans(n_clusters=n, random_state=42)

kmeans.fit(X_scaled)

distances.append(kmeans.inertia_)

plt.figure(figsize=(7, 5))

plt.plot(range(2, max_clusters+1), distances, marker='o')

plt.title('肘部法则')

plt.xlabel('簇数')

plt.ylabel('平方距离之和')

plt.xticks(range(2, max_clusters+1))

plt.grid(True)

plt.show()

return distances

distances = determine_optimal_clusters(X_scaled)

我们可以使用上述代码生成惯性与簇数的关系图。

肘部法则

当 K=1 时，惯性最高。从 K=1 到 K=5，惯性急剧下降。在 K=5 到 K=7 之间，曲线逐渐下降。最后，当 K=7 时，曲线变得稳定，因此 K 的最佳值为 7。

可视化细分结果

让我们实现 K-均值聚类算法并可视化结果。

# Apply K-means clustering with the chosen number of clusters
chosen_clusters = 7  
kmeans = KMeans(n_clusters=chosen_clusters, random_state=42)
kmeans.fit(X_scaled)

# Get cluster labels
cluster_labels = kmeans.labels_

# Add the cluster labels to the original dataframe
df['Cluster'] = cluster_labels

# Visualize the clusters in 3D
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Scatter plot for each cluster
for cluster in range(chosen_clusters):
    cluster_data = df[df['Cluster'] == cluster]
    ax.scatter(cluster_data['Quantity'], cluster_data['UnitPrice'], cluster_data['CustomerID'],
               label=f'Cluster {cluster}', s=50)

ax.set_xlabel('Quantity')
ax.set_ylabel('UnitPrice')
ax.set_zlabel('CustomerID')

# Add a legend
ax.legend()
plt.show()

# 使用选择的簇数应用 K-均值聚类

chosen_clusters = 7

kmeans = KMeans(n_clusters=chosen_clusters, random_state=42)

kmeans.fit(X_scaled)

# 获取簇标签

cluster_labels = kmeans.labels_

# 将簇标签添加到原始数据框

df['Cluster'] = cluster_labels

# 在 3D 中可视化簇

fig = plt.figure(figsize=(12, 8))

ax = fig.add_subplot(111, projection='3d')

# 每个簇的散点图

for cluster in range(chosen_clusters):

cluster_data = df[df['Cluster'] == cluster]

ax.scatter(cluster_data['Quantity'], cluster_data['UnitPrice'], cluster_data['CustomerID'],

label=f'簇 {cluster}', s=50)

ax.set_xlabel('数量')

ax.set_ylabel('单价')

ax.set_zlabel('客户ID')

# 添加图例

ax.legend()

plt.show()

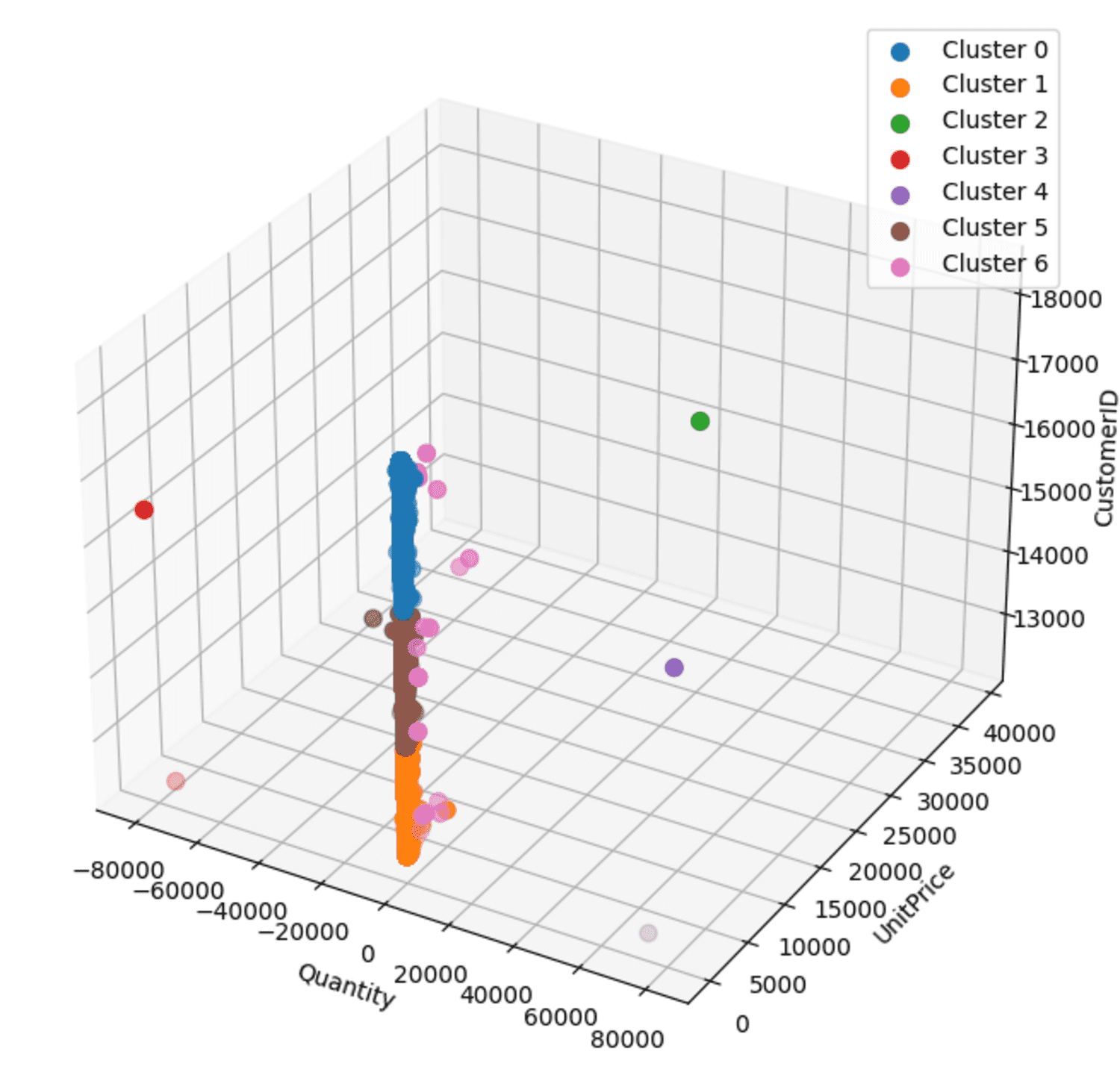
散点图

3D 散点图根据“数量”、“单价”和“客户 ID”可视化了簇。每个簇都用不同的颜色区分并相应地标记。

结论

我们讨论了使用机器学习进行客户细分及其优点。此外，我们展示了如何实现 K-均值算法将客户细分为不同的群体。首先，我们使用肘部法则找到了合适的簇数。然后，我们实现了 K-均值算法并使用散点图可视化了结果。通过这些步骤，公司可以有效地将客户细分为不同的群体。

导航