您可能一直被告知要标准化或归一化输入模型以提高性能。但什么是归一化,我们如何在深度学习模型中轻松实现它以提高性能?归一化我们的输入旨在创建一组相互之间尺度相同的特征,这一点我们将在本文中更详细地探讨。
此外,考虑到这一点,在神经网络中,每一层的输出都作为下一层的输入,因此一个自然的问题是:如果对模型进行输入归一化有助于提高模型性能,那么对每一层的输入进行标准化是否也有助于提高模型性能呢?
大多数情况下答案是肯定的!然而,与对整个模型的输入进行归一化不同,对中间层的输入进行归一化会更复杂一些,因为激活值在不断变化。因此,不可能,或者至少在计算上是昂贵的,一遍又一遍地持续计算整个训练集上的统计数据。在本文中,我们将探讨归一化层以对模型的输入进行归一化,以及批归一化,这是一种跨批次对每一层的输入进行标准化的技术。
让我们开始吧!

使用归一化层改善深度学习模型
Matej 拍摄的照片。保留部分权利。
概述
本教程分为 6 个部分;它们是
- 什么是归一化及其原因?
- 在 TensorFlow 中使用归一化层
- 什么是批归一化以及我们为什么应该使用它?
- 批归一化:幕后
- 归一化和批归一化实战
什么是归一化及其原因?
归一化一组数据会将其转换为相似的尺度。对于机器学习模型,我们的目标通常是重新中心化和重新缩放我们的数据,使其根据数据本身在 0 到 1 或 -1 到 1 之间。完成此操作的一种常见方法是计算数据集的均值和标准差,然后通过减去均值并除以标准差来转换每个样本,如果我们假设数据遵循正态分布,则此方法很有用,因为它可以帮助我们标准化数据并实现标准正态分布。
归一化可以帮助训练我们的神经网络,因为不同的特征处于相似的尺度,这有助于稳定梯度下降步骤,使我们能够使用更大的学习率或帮助模型在给定学习率下更快地收敛。
在 TensorFlow 中使用归一化层
要在 TensorFlow 中归一化输入,我们可以使用 Keras 中的归一化层。首先,让我们定义一些样本数据,
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np sample1 = np.array([ [1, 1, 1], [1, 1, 1], [1, 1, 1] ], dtype=np.float32) sample2 = np.array([ [2, 2, 2], [2, 2, 2], [2, 2, 2] ], dtype=np.float32) sample3 = np.array([ [3, 3, 3], [3, 3, 3], [3, 3, 3] ], dtype=np.float32) |
然后我们初始化我们的归一化层。
|
1 2 3 4 |
import tensorflow as tf from tensorflow.keras.layers import Normalization normalization_layer = Normalization() |
然后,为了获取数据集的均值和标准差并将我们的归一化层设置为使用这些参数,我们可以调用 `Normalization.adapt()` 方法处理我们的数据。
|
1 2 3 4 5 |
combined_batch = tf.constant(np.expand_dims(np.stack([sample1, sample2, sample3]), axis=-1), dtype=tf.float32) normalization_layer = Normalization() normalization_layer.adapt(combined_batch) |
在这种情况下,我们使用 `expand_dims` 添加了一个额外的维度,因为归一化层默认沿最后一个维度进行归一化(最后一个维度的每个索引都有自己的均值和方差参数在训练集上计算),因为这被认为是特征维度,对于 RGB 图像来说,这通常就是不同的颜色维度。
然后,为了对数据进行归一化,我们可以像这样调用归一化层处理数据,
|
1 |
normalization_layer(sample1) |
其输出为
|
1 2 3 4 |
<tf.Tensor: shape=(1, 1, 3, 3), dtype=float32, numpy= array([[[[-1.2247449, -1.2247449, -1.2247449], [-1.2247449, -1.2247449, -1.2247449], [-1.2247449, -1.2247449, -1.2247449]]]], dtype=float32)> |
我们可以通过对原始数据运行 `np.mean` 和 `np.std` 来验证这是否是预期的行为,它们分别给出均值为 2.0 和标准差为 0.8165。对于输入值 $$-1$$,我们有 $$(-1-2)/0.8165 = -1.2247$$。
既然我们已经了解了如何对输入进行归一化,让我们来看看另一种归一化方法,批归一化。
什么是批归一化以及我们为什么应该使用它?
从名字上看,您可能已经猜到批归一化一定与训练期间的批次有关。简单来说,批归一化对单个批次中层的输入进行标准化。
您可能会想,为什么我们不能直接计算给定层的均值和方差并以此方式进行归一化呢?问题出现在我们训练模型时,因为参数在训练过程中会发生变化,因此中间层的激活值在不断变化,为每次迭代计算整个训练集的均值和方差将非常耗时,而且可能毫无意义,因为激活值在每次迭代时都会改变。这就是批归一化的用武之地。
批归一化在 Ioffe 和 Szegedy 的论文“Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift”中被引入,它通过标准化层的输入来解决内部协变量偏移问题。在论文中,内部协变量偏移被定义为“每个层输入的分布在训练期间会发生变化,因为前一层的参数会发生变化”的问题。
批归一化解决内部协变量偏移问题的想法受到了质疑,尤其是在 Santurkar 等人的论文“How Does Batch Normalization Help Optimization?”中,他们提出批归一化实际上有助于平滑损失函数在参数空间中的变化。虽然批归一化如何做到这一点可能并不总是清楚,但它在许多不同的问题和模型上都取得了良好的经验结果。
也有一些证据表明,批归一化可以显著有助于解决深度学习模型中常见的梯度消失问题。在原始的 ResNet 论文中,He 等人在分析 ResNet 与普通网络时提到,“即使在普通网络中,使用 BN(批归一化)进行的梯度反向传播也表现出健康的范数”。
也有人建议批归一化还有其他好处,例如允许我们使用更高的学习率,因为批归一化可以帮助稳定参数增长。它还可以帮助正则化模型。根据原始的批归一化论文,
“使用批归一化进行训练时,训练样本与小批量中的其他样本一起被看到,并且训练网络不再为给定训练样本产生确定性值。在我们的实验中,我们发现这种效果对网络的泛化是有利的。”
批归一化:幕后
那么,批归一化实际上做了什么?
首先,我们需要计算批次统计数据,特别是每个激活值在批次中的均值和方差。由于神经网络中每一层的输出都作为下一层的输入,通过标准化层的输出,我们也标准化了模型中下一层的输入(尽管实际上,在原始论文中建议在激活函数之前实现批归一化,但对此存在一些争论)。
所以,我们计算
然后,对于每个激活图,我们使用相应的统计数据对每个值进行归一化
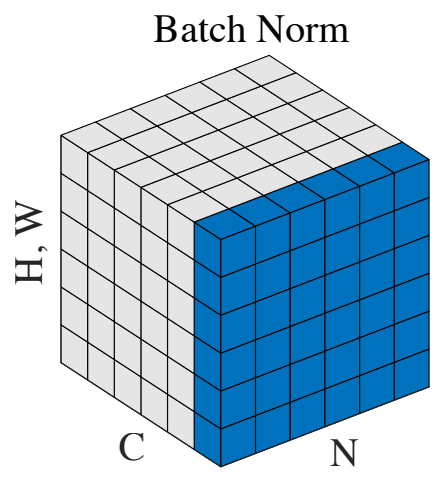
特别是对于卷积神经网络(CNN),我们对同一通道的所有位置计算这些统计数据。因此,每个通道将有一个 $$\hat\mu$$ 和 $$s^2$$,它们将应用于同一批次中每个样本的同一通道的所有像素。根据原始的批归一化论文,
“对于卷积层,我们还希望归一化服从卷积属性——以便同一特征图的不同元素在不同位置以相同的方式进行归一化。”
既然我们已经了解了如何计算归一化激活图,让我们来看看如何使用 Numpy 数组实现它。
假设我们有这些激活图,它们都代表单个通道,
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np activation_map_sample1 = np.array([ [1, 1, 1], [1, 1, 1], [1, 1, 1] ], dtype=np.float32) activation_map_sample2 = np.array([ [1, 2, 3], [4, 5, 6], [7, 8, 9] ], dtype=np.float32) activation_map_sample3 = np.array([ [9, 8, 7], [6, 5, 4], [3, 2, 1] ], dtype=np.float32) |
然后,我们希望标准化激活图中的每个元素,跨所有位置和跨不同样本。为了标准化,我们使用以下方法计算它们的均值和标准差
|
1 2 3 4 5 6 7 8 |
#获取批次中不同样本的激活均值 activation_mean_bn = np.mean([activation_map_sample1, activation_map_sample2, activation_map_sample3], axis=0) #获取批次中不同样本的激活标准差 activation_std_bn = np.std([activation_map_sample1, activation_map_sample2, activation_map_sample3], axis=0) print (activation_mean_bn) print (activation_std_bn) |
输出为
|
1 2 |
3.6666667 2.8284268 |
然后,我们可以通过以下方式标准化激活图:
|
1 2 |
#获取样本 1 的批归一化激活图 activation_map_sample1_bn = (activation_map_sample1 - activation_mean_bn) / activation_std_bn |
这些存储了输出
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
activation_map_sample1_bn: [[-0.94280916 -0.94280916 -0.94280916] [-0.94280916 -0.94280916 -0.94280916] [-0.94280916 -0.94280916 -0.94280916]] activation_map_sample2_bn: [[-0.94280916 -0.58925575 -0.2357023 ] [ 0.11785112 0.47140455 0.82495797] [ 1.1785114 1.5320647 1.8856182 ]] activation_map_sample3_bn: [[ 1.8856182 1.5320647 1.1785114 ] [ 0.82495797 0.47140455 0.11785112] [-0.2357023 -0.58925575 -0.94280916]] |
但我们在推理时遇到了一个障碍。如果在推理时没有示例批次怎么办,即使有,如果输出是由输入确定性计算的,那也是更可取的。所以,我们需要计算一组固定的参数以供推理时使用。为此,我们存储均值和方差的移动平均值,并在推理时使用它们来计算层的输出。
然而,仅通过这种方式标准化模型输入还有一个问题,那就是它改变了层的表示能力。批归一化论文中提出的一个例子是 sigmoid 非线性函数,其中标准化输入会将其约束在 sigmoid 函数的线性范围内。为了解决这个问题,又添加了一个线性层来缩放和重新中心化值,并带有 2 个可训练参数来学习应使用的适当尺度和中心。
在 TensorFlow 中实现批归一化
现在我们了解了批归一化在幕后的工作原理,让我们看看如何在深度学习模型中使用 Keras 的批归一化层。
要在 TensorFlow 中将批归一化作为深度学习模型的一部分来实现,我们可以使用 `keras.layers.BatchNormalization` 层。使用我们之前示例中的 Numpy 数组,我们可以对它们实现 BatchNormalization。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import tensorflow as tf import tensorflow.keras as keras from tensorflow.keras.layers import BatchNormalization import numpy as np # 扩展维度以创建通道 activation_maps = tf.constant(np.expand_dims(np.stack([ activation_map_sample1, activation_map_sample2, activation_map_sample3 ]), axis=0),dtype=tf.float32) print (f"activation_maps: \n{activation_maps}\n") print (BatchNormalization(axis=0)(activation_maps, training=True)) |
输出结果为
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
activation_maps: [[[[1. 1. 1.] [1. 1. 1.] [1. 1. 1.]] [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] [[9. 8. 7.] [6. 5. 4.] [3. 2. 1.]]]] tf.Tensor( [[[[-0.9427501 -0.9427501 -0.9427501 ] [-0.9427501 -0.9427501 -0.9427501 ] [-0.9427501 -0.9427501 -0.9427501 ]] [[-0.9427501 -0.5892188 -0.2356875 ] [ 0.11784375 0.471375 0.82490635] [ 1.1784375 1.5319688 1.8855002 ]] [[ 1.8855002 1.5319688 1.1784375 ] [ 0.82490635 0.471375 0.11784375] [-0.2356875 -0.5892188 -0.9427501 ]]], shape=(1, 3, 3, 3), dtype=float32) |
默认情况下,BatchNormalization 层对于线性层使用 1 的尺度和 0 的中心,因此这些值与我们之前使用 Numpy 函数计算的值相似。
归一化和批归一化实战
既然我们已经了解了如何在 TensorFlow 中实现归一化和批归一化层,让我们来探讨一个使用归一化和批归一化层的 LeNet-5 模型,并将其与不使用这些层的模型进行比较。
首先,我们获取数据集,在此示例中我们将使用 CIFAR-10。
|
1 |
(trainX, trainY), (testX, testY) = keras.datasets.cifar10.load_data() |
使用带有 ReLU 激活的 LeNet-5 模型,
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
from tensorflow.keras.layers import Dense, Input, Flatten, Conv2D, MaxPool2D from tensorflow.keras.models import Model import tensorflow as tf class LeNet5(tf.keras.Model): def __init__(self): super(LeNet5, self).__init__() def call(self, input_tensor): self.conv1 = Conv2D(filters=6, kernel_size=(5,5), padding="same", activation="relu")(input_tensor) self.maxpool1 = MaxPool2D(pool_size=(2,2))(self.conv1) self.conv2 = Conv2D(filters=16, kernel_size=(5,5), padding="same", activation="relu")(self.maxpool1) self.maxpool2 = MaxPool2D(pool_size=(2, 2))(self.conv2) self.flatten = Flatten()(self.maxpool2) self.fc1 = Dense(units=120, activation="relu")(self.flatten) self.fc2 = Dense(units=84, activation="relu")(self.fc1) self.fc3 = Dense(units=10, activation="sigmoid")(self.fc2) return self.fc3 input_layer = Input(shape=(32,32,3,)) x = LeNet5()(input_layer) model = Model(inputs=input_layer, outputs=x) model.compile(optimizer="adam", loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics="acc") history = model.fit(x=trainX, y=trainY, batch_size=256, epochs=10, validation_data=(testX, testY)) |
训练模型给出的输出为:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Epoch 1/10 196/196 [==============================] - 14s 15ms/step - loss: 3.8905 - acc: 0.2172 - val_loss: 1.9656 - val_acc: 0.2853 Epoch 2/10 196/196 [==============================] - 2秒 12毫秒/步 - loss: 1.8402 - acc: 0.3375 - val_loss: 1.7654 - val_acc: 0.3678 Epoch 3/10 196/196 [==============================] - 2秒 12毫秒/步 - loss: 1.6778 - acc: 0.3986 - val_loss: 1.6484 - val_acc: 0.4039 Epoch 4/10 196/196 [==============================] - 2秒 12毫秒/步 - loss: 1.5663 - acc: 0.4355 - val_loss: 1.5644 - val_acc: 0.4380 Epoch 5/10 196/196 [==============================] - 2秒 12毫秒/步 - loss: 1.4815 - acc: 0.4712 - val_loss: 1.5357 - val_acc: 0.4472 Epoch 6/10 196/196 [==============================] - 2秒 12毫秒/步 - loss: 1.4053 - acc: 0.4975 - val_loss: 1.4883 - val_acc: 0.4675 Epoch 7/10 196/196 [==============================] - 2秒 12毫秒/步 - loss: 1.3300 - acc: 0.5262 - val_loss: 1.4643 - val_acc: 0.4805 Epoch 8/10 196/196 [==============================] - 2秒 12毫秒/步 - loss: 1.2595 - acc: 0.5531 - val_loss: 1.4685 - val_acc: 0.4866 Epoch 9/10 196/196 [==============================] - 2秒 12毫秒/步 - loss: 1.1999 - acc: 0.5752 - val_loss: 1.4302 - val_acc: 0.5026 Epoch 10/10 196/196 [==============================] - 2秒 12毫秒/步 - loss: 1.1370 - acc: 0.5979 - val_loss: 1.4441 - val_acc: 0.5009 |
接下来,我们看看如果添加归一化和批量归一化层会发生什么。我们通常添加层归一化。修改我们的LeNet-5模型,
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
class LeNet5_Norm(tf.keras.Model): def __init__(self, norm_layer, *args, **kwargs): super(LeNet5_Norm, self).__init__() self.conv1 = Conv2D(filters=6, kernel_size=(5,5), padding="same") self.norm1 = norm_layer(*args, **kwargs) self.relu = relu self.max_pool2x2 = MaxPool2D(pool_size=(2,2)) self.conv2 = Conv2D(filters=16, kernel_size=(5,5), padding="same") self.norm2 = norm_layer(*args, **kwargs) self.flatten = Flatten() self.fc1 = Dense(units=120) self.norm3 = norm_layer(*args, **kwargs) self.fc2 = Dense(units=84) self.norm4 = norm_layer(*args, **kwargs) self.fc3 = Dense(units=10, activation="softmax") def call(self, input_tensor): conv1 = self.conv1(input_tensor) conv1 = self.norm1(conv1) conv1 = self.relu(conv1) maxpool1 = self.max_pool2x2(conv1) conv2 = self.conv2(maxpool1) conv2 = self.norm2(conv2) conv2 = self.relu(conv2) maxpool2 = self.max_pool2x2(conv2) flatten = self.flatten(maxpool2) fc1 = self.fc1(flatten) fc1 = self.norm3(fc1) fc1 = self.relu(fc1) fc2 = self.fc2(fc1) fc2 = self.norm4(fc2) fc2 = self.relu(fc2) fc3 = self.fc3(fc2) return fc3 |
再次运行训练,这次添加了归一化层。
|
1 2 3 4 5 6 7 8 9 10 11 |
normalization_layer = Normalization() normalization_layer.adapt(trainX) input_layer = Input(shape=(32,32,3,)) x = LeNet5_Norm(BatchNormalization)(normalization_layer(input_layer)) model = Model(inputs=input_layer, outputs=x) model.compile(optimizer="adam", loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics="acc") history = model.fit(x=trainX, y=trainY, batch_size=256, epochs=10, validation_data=(testX, testY)) |
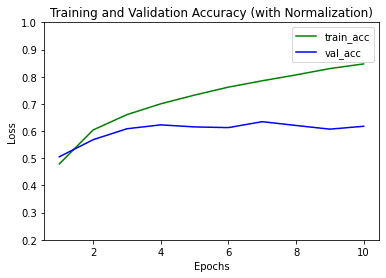
我们看到模型收敛得更快,并且验证准确率更高。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Epoch 1/10 196/196 [==============================] - 5秒 17毫秒/步 - loss: 1.4643 - acc: 0.4791 - val_loss: 1.3837 - val_acc: 0.5054 Epoch 2/10 196/196 [==============================] - 3秒 14毫秒/步 - loss: 1.1171 - acc: 0.6041 - val_loss: 1.2150 - val_acc: 0.5683 Epoch 3/10 196/196 [==============================] - 3秒 14毫秒/步 - loss: 0.9627 - acc: 0.6606 - val_loss: 1.1038 - val_acc: 0.6086 Epoch 4/10 196/196 [==============================] - 3秒 14毫秒/步 - loss: 0.8560 - acc: 0.7003 - val_loss: 1.0976 - val_acc: 0.6229 Epoch 5/10 196/196 [==============================] - 3秒 14毫秒/步 - loss: 0.7644 - acc: 0.7325 - val_loss: 1.1073 - val_acc: 0.6153 Epoch 6/10 196/196 [==============================] - 3秒 15毫秒/步 - loss: 0.6872 - acc: 0.7617 - val_loss: 1.1484 - val_acc: 0.6128 Epoch 7/10 196/196 [==============================] - 3秒 14毫秒/步 - loss: 0.6229 - acc: 0.7850 - val_loss: 1.1469 - val_acc: 0.6346 Epoch 8/10 196/196 [==============================] - 3秒 14毫秒/步 - loss: 0.5583 - acc: 0.8067 - val_loss: 1.2041 - val_acc: 0.6206 Epoch 9/10 196/196 [==============================] - 3秒 15毫秒/步 - loss: 0.4998 - acc: 0.8300 - val_loss: 1.3095 - val_acc: 0.6071 Epoch 10/10 196/196 [==============================] - 3秒 14毫秒/步 - loss: 0.4474 - acc: 0.8471 - val_loss: 1.2649 - val_acc: 0.6177 |
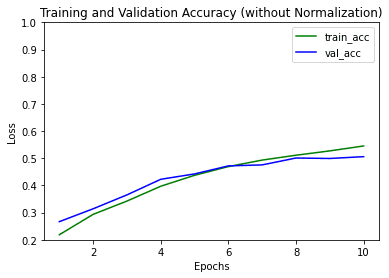
绘制两个模型的训练和验证准确率图,
使用批量归一化时的一些注意事项,通常不建议将批量归一化与Dropout一起使用,因为批量归一化具有正则化效果。另外,太小的批量大小可能是批量归一化的问题,因为计算出的统计量(均值和方差)的质量受批量大小影响,而非常小的批量大小可能导致问题,极端情况是如果看简单的神经网络,一个样本的所有激活值都为0。如果您考虑使用小的批量大小,请考虑使用层归一化(在下面的“进一步阅读”部分有更多资源)。
这是包含归一化层的模型的完整代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
from tensorflow.keras.layers import Dense, Input, Flatten, Conv2D, BatchNormalization, MaxPool2D, Normalization from tensorflow.keras.models import Model import tensorflow as tf import tensorflow.keras as keras class LeNet5_Norm(tf.keras.Model): def __init__(self, norm_layer, *args, **kwargs): super(LeNet5_Norm, self).__init__() self.conv1 = Conv2D(filters=6, kernel_size=(5,5), padding="same") self.norm1 = norm_layer(*args, **kwargs) self.relu = relu self.max_pool2x2 = MaxPool2D(pool_size=(2,2)) self.conv2 = Conv2D(filters=16, kernel_size=(5,5), padding="same") self.norm2 = norm_layer(*args, **kwargs) self.flatten = Flatten() self.fc1 = Dense(units=120) self.norm3 = norm_layer(*args, **kwargs) self.fc2 = Dense(units=84) self.norm4 = norm_layer(*args, **kwargs) self.fc3 = Dense(units=10, activation="softmax") def call(self, input_tensor): conv1 = self.conv1(input_tensor) conv1 = self.norm1(conv1) conv1 = self.relu(conv1) maxpool1 = self.max_pool2x2(conv1) conv2 = self.conv2(maxpool1) conv2 = self.norm2(conv2) conv2 = self.relu(conv2) maxpool2 = self.max_pool2x2(conv2) flatten = self.flatten(maxpool2) fc1 = self.fc1(flatten) fc1 = self.norm3(fc1) fc1 = self.relu(fc1) fc2 = self.fc2(fc1) fc2 = self.norm4(fc2) fc2 = self.relu(fc2) fc3 = self.fc3(fc2) return fc3 # 加载数据集,使用cifar10以显示更高的准确率提升 (trainX, trainY), (testX, testY) = keras.datasets.cifar10.load_data() normalization_layer = Normalization() normalization_layer.adapt(trainX) input_layer = Input(shape=(32,32,3,)) x = LeNet5_Norm(BatchNormalization)(normalization_layer(input_layer)) model = Model(inputs=input_layer, outputs=x) model.compile(optimizer="adam", loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics="acc") history = model.fit(x=trainX, y=trainY, batch_size=256, epochs=10, validation_data=(testX, testY)) |
进一步阅读
论文
- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
- How Does Batch Normalization Help Optimization?
- Deep Residual Learning for Image Recognition (ResNet论文)
您可以在模型中实现的几种不同类型的归一化方法如下:
Tensorflow 层
- Tensorflow 插件(层、实例、组归一化): https://github.com/tensorflow/addons/blob/master/docs/tutorials/layers_normalizations.ipynb
- 批归一化
- 归一化
结论
在这篇文章中,您了解了归一化和批归一化是如何工作的,以及如何在 TensorFlow 中实现它们。您还看到了使用这些层如何能够显著提高机器学习模型的性能。
具体来说,您已经学会了
- 归一化和批归一化有什么作用
- 如何在 TensorFlow 中使用归一化和批归一化
- 在使用批归一化进行机器学习模型时的一些技巧
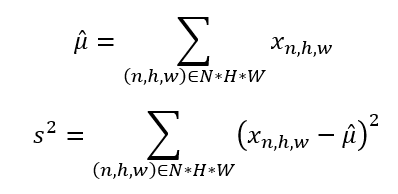
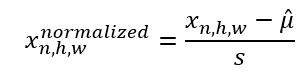



老师您好,
这个教程非常有帮助,而且容易学习。此外,我想学习一下:
如何使用财务比率数据集进行准确的模型预测?
例如,为期一年的 200 家公司的信用风险(7-14 个比率)(横截面数据集)。
恳请您给予有益的评论。
谢谢你
您好 Waheed……您可能会对以下内容感兴趣
https://towardsdatascience.com/credit-risk-modeling-with-machine-learning-8c8a2657b4c4
谢谢,我觉得这终于帮助我清楚地理解了批归一化与层归一化的区别。我之前没想到对于 CNN,我们是在批次中对每个通道单独进行归一化。这很合理,因为每个通道/特征可能有截然不同的均值和标准差,这是可以的。我也很清楚为什么我们需要存储批归一化统计数据的移动平均值。我注意到 Keras 中有一个 LayerNormalization 层。这与您代码中的 Normalization 层不同吗?
不客气,Jamison!概念是相似的,并且在以下资源中提供了更多详细信息
https://arxiv.org/abs/1607.06450
https://keras.org.cn/api/layers/normalization_layers/layer_normalization/
图表中有一个拼写错误——应该是 accuracy(准确率)而不是 loss(损失)。
感谢您的反馈 Dmitry!
您忘了除以样本数量来归一化维度或(样本数量 - 1)来使其无偏。
您好 anonymous……感谢您的反馈!从纯粹的统计学角度来看,您是正确的。以下资源可能有助于阐明归一化和标准化在机器学习中的使用。
https://machinelearning.org.cn/standardscaler-and-minmaxscaler-transforms-in-python/
假设我们已经用上述归一化技术训练了我们的图像数据集。在测试时,我们是否也应该手动归一化测试数据集,减去训练集的均值并除以方差?还是 model.evaluate() 方法已经处理了?
您好……以下资源可能可以阐明归一化和标准化的使用。
https://machinelearning.org.cn/standardscaler-and-minmaxscaler-transforms-in-python/