函数优化涉及查找产生目标函数最优值的输入。
优化算法在搜索空间中导航输入变量以定位极值,并且目标函数的形状以及算法在搜索空间中的行为在现实世界的问题中是模糊不清的。
因此,通常使用可以轻松直接可视化的简单低维函数来研究优化算法。此外,优化算法在这些简单函数的输入空间中产生的样本也可以与它们相应的上下文一起可视化。
可视化低维函数和算法在这些函数上的行为,可以帮助我们培养直觉,这些直觉可以迁移到之后更复杂的高维函数优化问题。
在本教程中,您将了解如何在Python中创建函数优化可视化。
完成本教程后,您将了解:
- 可视化是研究函数优化算法时的重要工具。
- 如何使用折线图可视化一维函数和样本。
- 如何使用等高线图和曲面图可视化二维函数和样本。
开始你的项目,阅读我的新书《机器学习优化》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
Python中函数优化的可视化
图片作者:Nathalie,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 函数优化可视化
- 可视化一维函数优化
- 测试函数
- 样本测试函数
- 测试函数折线图
- 测试函数散点图
- 标示最优值的折线图
- 带样本的折线图
- 可视化二维函数优化
- 测试函数
- 样本测试函数
- 测试函数等高线图
- 测试函数填充等高线图
- 带样本的测试函数填充等高线图
- 测试函数曲面图
函数优化可视化
函数优化是一个数学领域,主要研究找出使函数输出最优(通常是最小值或最大值)的输入。
对于简单的可解析计算的微分函数,优化可能很简单。然而,在应用机器学习中,我们感兴趣的大多数函数可能行为良好,也可能行为不佳,并且可能复杂、非线性、多变量且不可微。
因此,了解可用于解决函数优化问题的各种算法非常重要。
研究函数优化的一个重要方面是理解正在优化的目标函数以及优化算法随时间的行为。
可视化在开始学习函数优化时起着重要作用。
我们可以选择简单且易于理解的测试函数来研究优化算法。这些简单的函数可以绘制出来,以理解目标函数的输入与目标函数的输出之间的关系,并突出显示山丘、山谷和最优值。
此外,优化算法在搜索空间中选择的样本也可以绘制在目标函数图的上方。这些算法行为图可以提供关于特定优化算法如何工作以及如何在搜索空间中导航的见解和直觉,这些见解和直觉可以推广到未来的新问题。
通常,选择一维或二维函数来研究优化算法,因为它们易于使用标准图(如折线图和曲面图)进行可视化。在本教程中我们将两者都进行探讨。
首先,让我们探讨一下如何可视化一维函数优化。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
可视化一维函数优化
一维函数接受一个输入变量,并输出该输入变量的评估值。
输入变量通常是连续的,用实值浮点数表示。通常,输入域没有约束,但对于测试问题,我们施加一个感兴趣的域。
测试函数
在这种情况下,我们将使用简单的 x^2 目标函数来探索函数可视化。
- f(x) = x^2
该函数在 x=0.0 的输入处具有最优值,其值为 0.0。
下面的示例实现了此目标函数并评估了单个输入。
|
1 2 3 4 5 6 7 8 9 10 |
# 1d 目标函数的示例 # 目标函数 def objective(x): return x**2.0 # 评估目标函数的输入 x = 4.0 result = objective(x) print('f(%.3f) = %.3f' % (x, result)) |
运行示例,目标函数评估值为 4.0,结果为 16.0。
|
1 |
f(4.000) = 16.000 |
对测试函数进行采样
对于新函数,我们首先想做的是定义一个感兴趣的输入范围,并使用均匀网格对感兴趣的域进行采样。
此样本将为稍后生成绘图提供基础。
在此情况下,我们将定义一个围绕 x=0.0 最优值(从 x=-5.0 到 x=5.0)的感兴趣域,并以 0.1 的增量对该范围内的网格值进行采样,例如 -5.0、-4.9、-4.8 等。
|
1 2 3 4 5 6 7 |
... # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 总结一些输入域 print(inputs[:5]) |
然后,我们可以评估样本中的每个 x 值。
|
1 2 3 4 5 |
... # 计算目标值 results = objective(inputs) # 总结一些结果 print(results[:5]) |
最后,我们可以检查一些输入及其对应的输出。
|
1 2 3 4 |
... # 创建一些输入到一些结果的映射 for i in range(5): print('f(%.3f) = %.3f' % (inputs[i], results[i])) |
将这些内容汇总,对采样输入空间并评估样本中所有点的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 采样 1d 目标函数 from numpy import arange # 目标函数 def objective(x): return x**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 总结一些输入域 print(inputs[:5]) # 计算目标值 results = objective(inputs) # 总结一些结果 print(results[:5]) # 创建一些输入到一些结果的映射 for i in range(5): print('f(%.3f) = %.3f' % (inputs[i], results[i])) |
运行示例,首先生成了我们期望的均匀输入点样本。
然后使用目标函数评估输入点,最后,我们可以看到输入到目标函数输出的简单映射。
|
1 2 3 4 5 6 7 |
[-5. -4.9 -4.8 -4.7 -4.6] [25. 24.01 23.04 22.09 21.16] f(-5.000) = 25.000 f(-4.900) = 24.010 f(-4.800) = 23.040 f(-4.700) = 22.090 f(-4.600) = 21.160 |
现在我们对生成输入样本并用目标函数评估它们有了信心,我们可以看看如何生成函数图。
测试函数折线图
我们可以随机采样输入空间,但均匀的线或网格的好处是它可以用于生成平滑的图。
它是平滑的,因为输入空间中的点是从小到大排序的。这种排序很重要,因为我们期望(希望)目标函数的输出在值之间具有相似的平滑关系,例如,输入值的微小变化会导致函数输出的局部一致(平滑)变化。
在这种情况下,我们可以使用样本生成目标函数的折线图,其中输入点 (x) 位于图的 x 轴上,目标函数输出 (results) 位于图的 y 轴上。
|
1 2 3 4 5 |
... # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 显示绘图 pyplot.show() |
将这些结合起来,完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 1d 目标函数的输入与结果的折线图 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return x**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 显示绘图 pyplot.show() |
运行示例,创建一个目标函数的折线图。
我们可以看到函数具有大的 U 形,称为抛物线。这是研究曲线时常见的形状,例如微积分的研究。
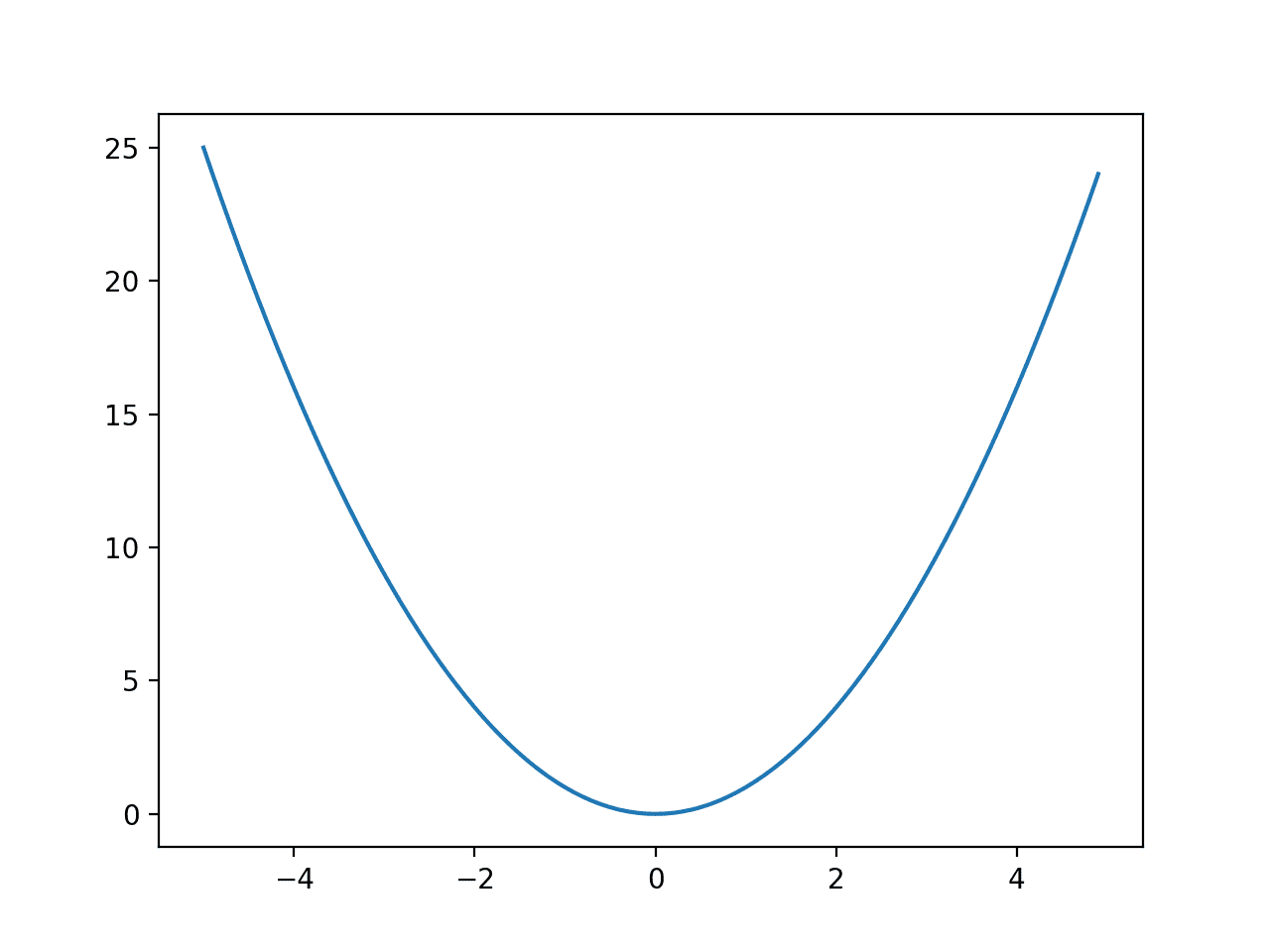
一维函数的折线图
测试函数散点图
这条线是一个构造。它不是真正的函数,只是函数的平滑摘要。请始终牢记这一点。
请记住,我们实际上生成了一个输入空间的点样本以及这些点的相应评估。
因此,创建点的散点图会更准确;例如
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 1d 目标函数的输入与结果的散点图 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return x**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = objective(inputs) # 创建输入与结果的散点图 pyplot.scatter(inputs, results) # 显示绘图 pyplot.show() |
运行示例,创建目标函数的散点图。
我们可以看到熟悉的函数形状,但直接绘制这些点并没有带来任何好处。
折线图及其提供的点之间的平滑插值更有用,因为我们可以将其他点绘制在折线图之上,例如最优值的位置或优化算法采样的点。
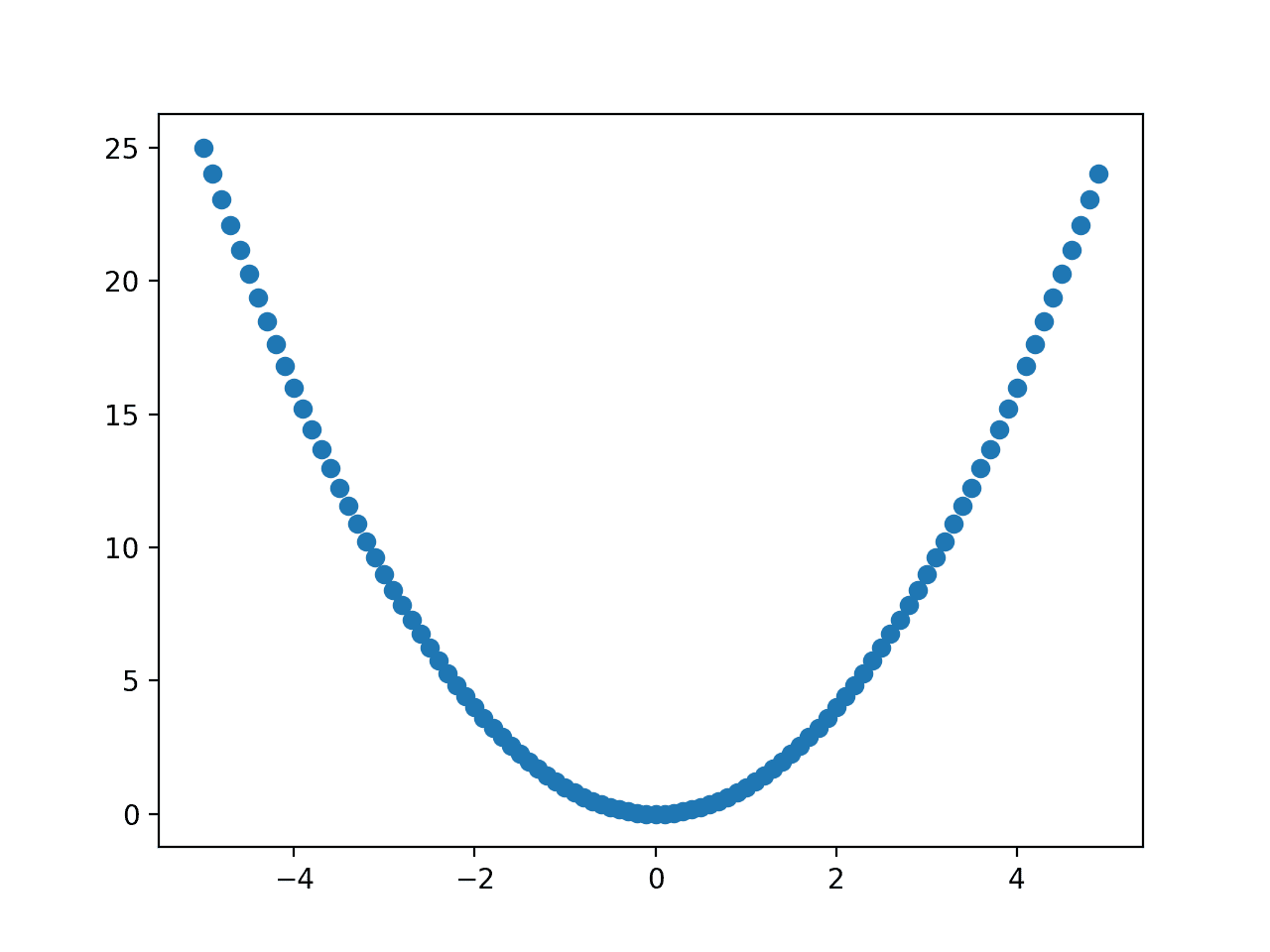
一维函数的散点图
标示最优值的折线图
接下来,让我们再次绘制折线图,这次绘制出函数已知最优值所在的位置。
这对于研究优化算法很有帮助,因为我们可能想看看优化算法能接近最优值的程度。
首先,我们必须定义最优值的输入,然后评估该点以获得用于绘图的 x 轴和 y 轴值。
|
1 2 3 4 |
... # 定义已知函数的最优值 optima_x = 0.0 optima_y = objective(optima_x) |
然后,我们可以使用我们喜欢的任何形状或颜色绘制该点,在此例中,是一个红色的方块。
|
1 2 3 |
... # 将函数最优值绘制成红色方块 pyplot.plot([optima_x], [optima_y], 's', color='r') |
将这些内容汇总,创建包含函数折线图并用点标示最优值的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 包含函数最优值的一维目标函数的输入与结果的折线图 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return x**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义已知函数的最优值 optima_x = 0.0 optima_y = objective(optima_x) # 将函数最优值绘制成红色方块 pyplot.plot([optima_x], [optima_y], 's', color='r') # 显示绘图 pyplot.show() |
运行示例,创建了熟悉的函数折线图,这次,函数的最优值,即产生函数最小输出的输入,用一个红色的方块标示出来。
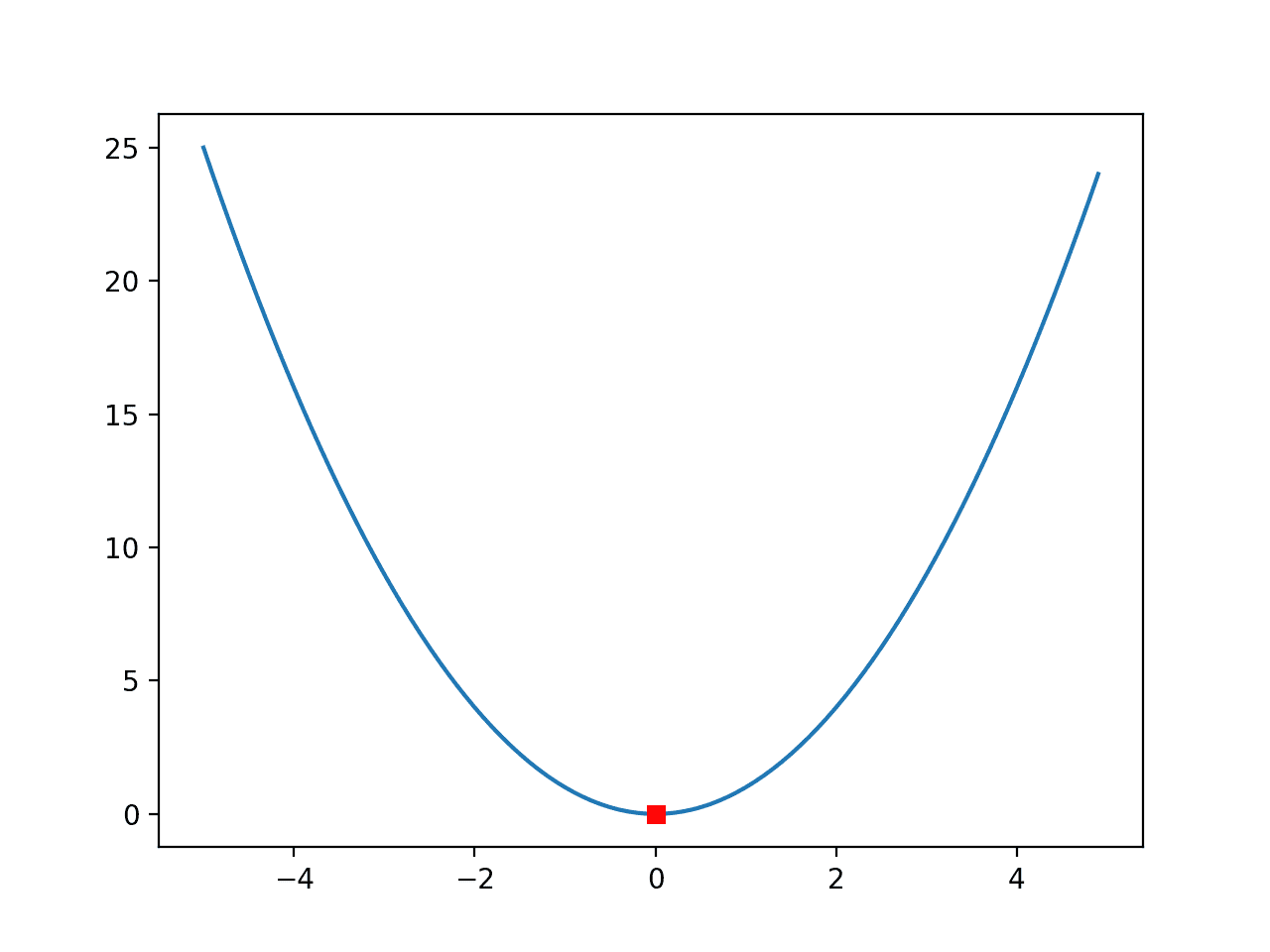
一维函数带红色方块标示最优值的折线图
这是一个非常简单的函数,红色的方块很容易看到最优值。
有时函数可能更复杂,有很多山丘和山谷,我们可能想让最优值更明显。
在这种情况下,我们可以绘制一条贯穿整个图的垂直线。
|
1 2 3 |
... # 在最优输入处画一条竖线 pyplot.axvline(x=optima_x, ls='--', color='red') |
将这些结合起来,完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 包含函数最优值作为线条的一维目标函数的输入与结果的折线图 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return x**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义已知函数的最优值 optima_x = 0.0 # 在最优输入处画一条竖线 pyplot.axvline(x=optima_x, ls='--', color='red') # 显示绘图 pyplot.show() |
运行示例,创建相同的图,这次绘制一条红线,清晰地标示出输入空间中标记最优值的位置。
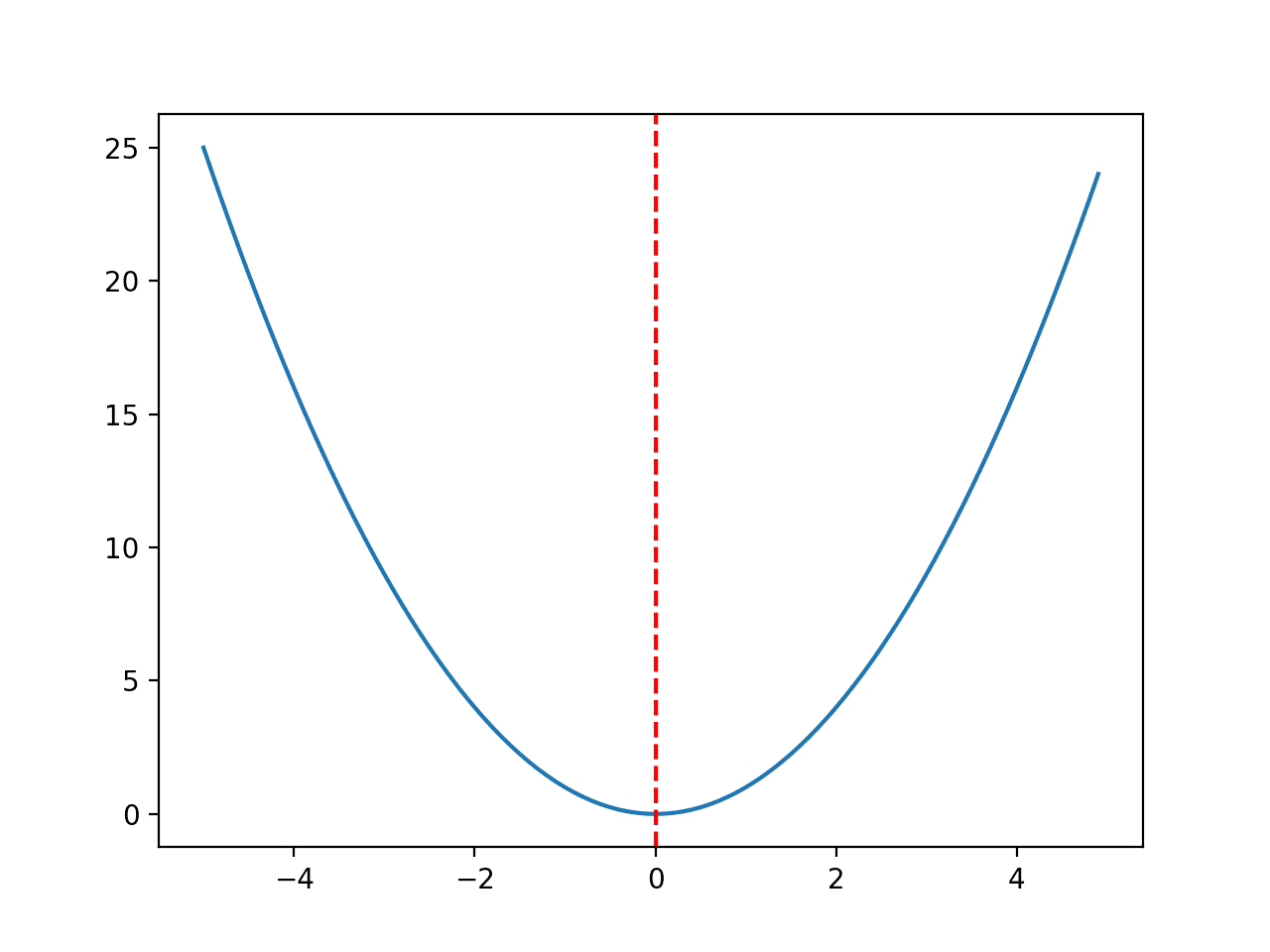
一维函数带红色线条标示最优值的折线图
带样本的折线图
最后,我们可能想绘制优化算法选择的输入空间样本。
我们将使用从输入域中随机抽取的点来模拟这些样本。
|
1 2 3 4 5 6 |
... # 模拟优化算法生成的样本 seed(1) sample = r_min + rand(10) * (r_max - r_min) # 评估样本 sample_eval = objective(sample) |
然后,我们可以绘制这个样本,在此例中,使用小的黑色圆点。
|
1 2 3 |
... # 将样本绘制为黑色圆圈 pyplot.plot(sample, sample_eval, 'o', color='black') |
包含函数折线图、最优值标记红线以及算法样本(用小黑点表示)的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# 包含最优值和算法样本的一维函数域的折线图 from numpy import arange from numpy.random import seed from numpy.random import rand from matplotlib import pyplot # 目标函数 def objective(x): return x**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = objective(inputs) # 模拟优化算法生成的样本 seed(1) sample = r_min + rand(10) * (r_max - r_min) # 评估样本 sample_eval = objective(sample) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义已知函数的最优值 optima_x = 0.0 # 在最优输入处画一条竖线 pyplot.axvline(x=optima_x, ls='--', color='red') # 将样本绘制为黑色圆圈 pyplot.plot(sample, sample_eval, 'o', color='black') # 显示绘图 pyplot.show() |
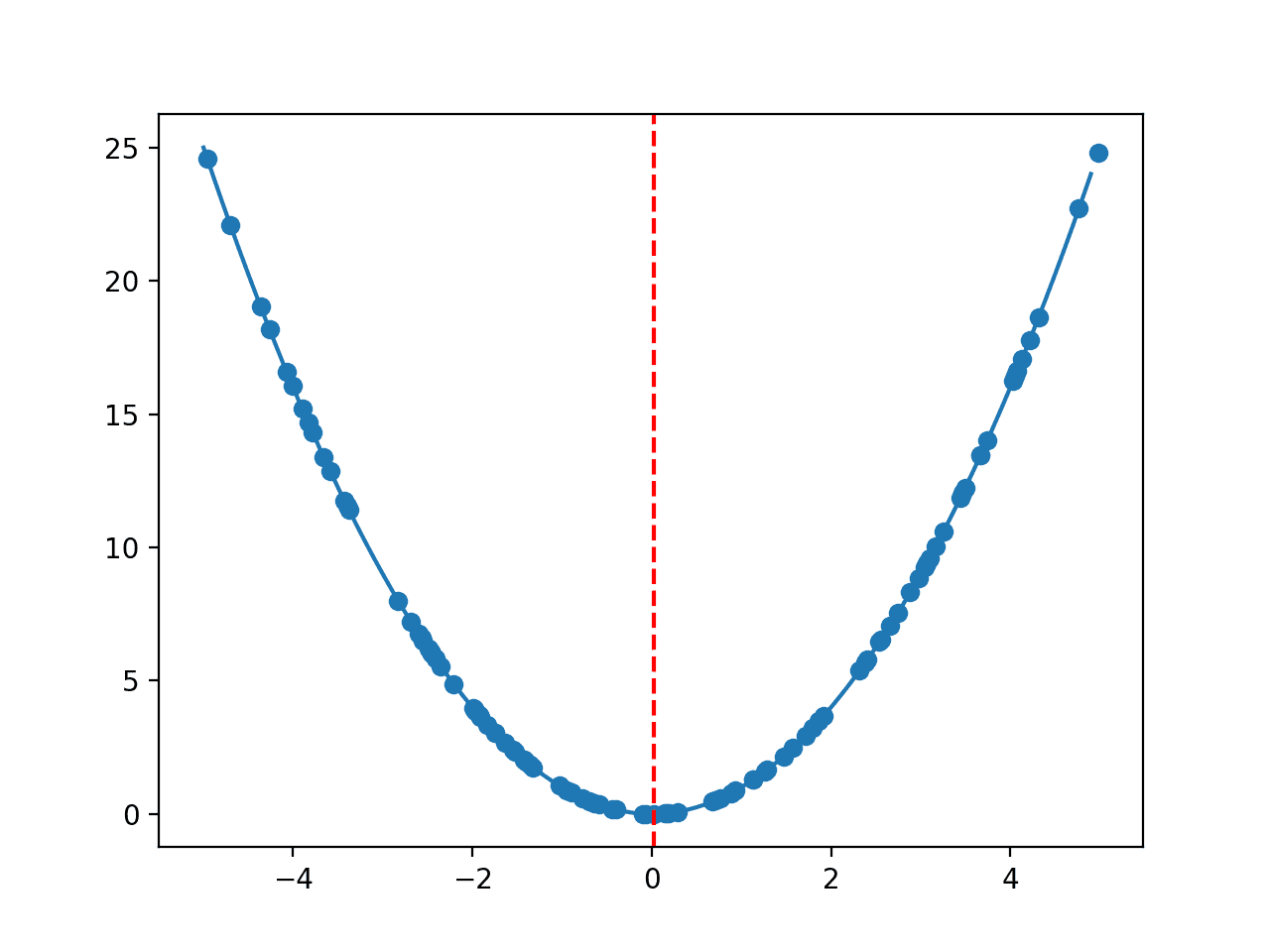
运行示例,创建了域的折线图,并像之前一样用红线标示了最优值。
这次,算法从域中选择的样本(实际上是随机点样本)用黑点绘制。
我们可以想象,一个真正的优化算法将显示点在搜索过程中从起始点向下坡收敛。
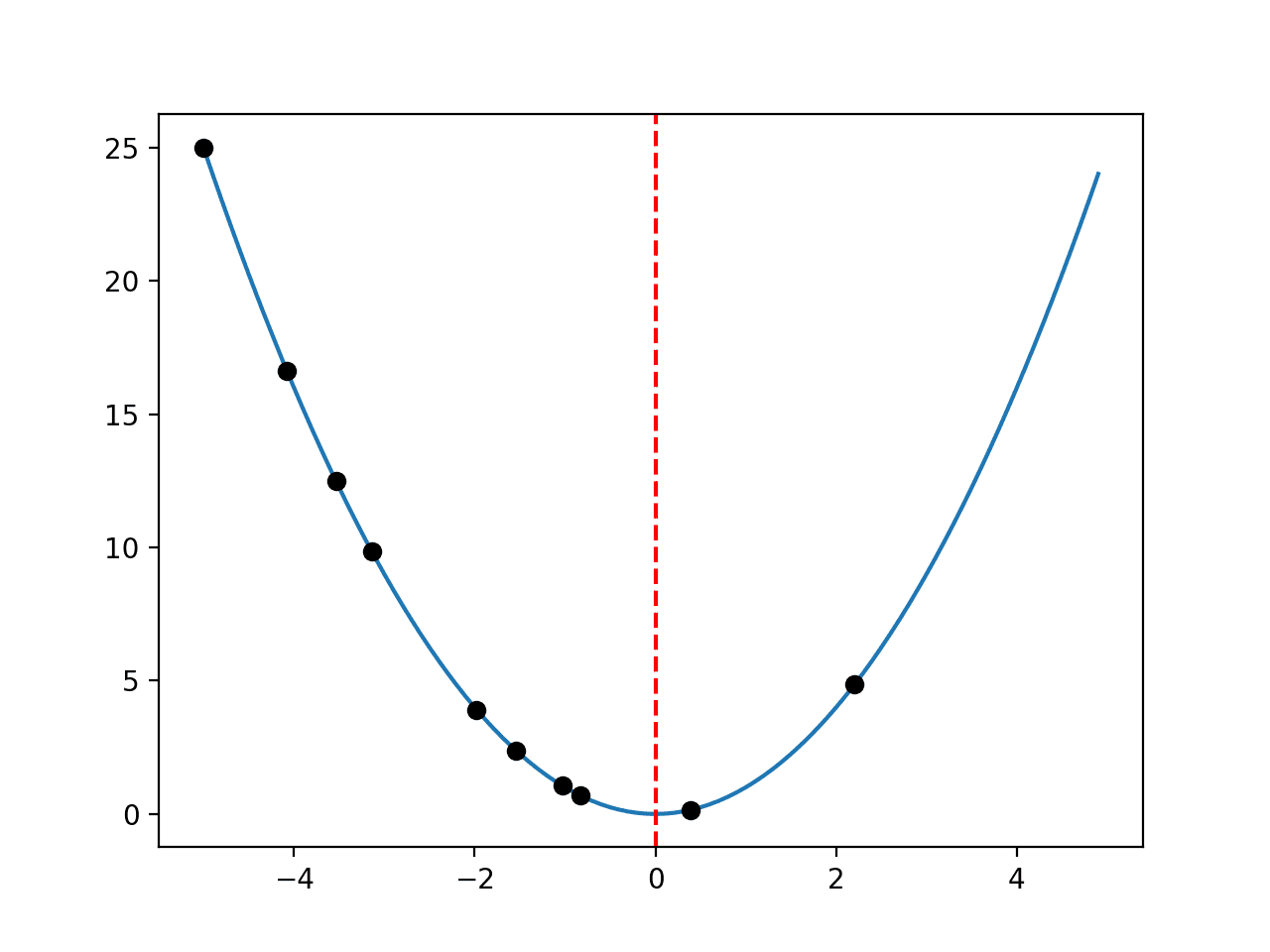
带红色线条标示最优值和黑色圆点样本的一维函数折线图
接下来,让我们看看如何为二维函数优化执行类似的Visualize。
可视化二维函数优化
二维函数是指接受两个输入变量的函数,例如 *x* 和 *y*。
测试函数
我们可以使用相同的 x^2 函数并将其扩展为一个二维函数;例如
- f(x, y) = x^2 + y^2
该函数在 [x=0.0, y=0.0] 的输入处具有最优值,其值为 0.0。
下面的示例实现了此目标函数并评估了单个输入。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 2d 目标函数的示例 # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 评估目标函数的输入 x = 4.0 y = 4.0 result = objective(x, y) print('f(%.3f, %.3f) = %.3f' % (x, y, result)) |
运行示例,评估点 [x=4, y=4],结果为 32。
|
1 |
f(4.000, 4.000) = 32.000 |
接下来,我们需要一种方法来对域进行采样,以便可以采样目标函数。
样本测试函数
对二维函数进行采样的一种常见方法是,首先沿每个变量(x 和 y)生成一个均匀样本,然后使用这两个均匀样本创建一个称为网格的样本。
这不是输入空间中的二维数组;而是两个二维数组,当它们一起使用时,定义了跨越两个输入变量的网格。
这是通过复制整个 x 样本数组来对应每个 y 样本点,类似地,复制整个 y 样本数组来对应每个 x 样本点来实现的。
可以使用 meshgrid() NumPy 函数来实现这一点;例如
|
1 2 3 4 5 6 7 8 9 10 |
... # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 总结一些输入域 print(x[:5, :5]) |
然后,我们可以使用目标函数评估每个点对。
|
1 2 3 4 5 |
... # 计算目标值 results = objective(x, y) # 总结一些结果 print(results[:5, :5]) |
最后,我们可以查看一些输入与其对应输出值的映射。
|
1 2 3 4 |
... # 创建一些输入到一些结果的映射 for i in range(5): print('f(%.3f, %.3f) = %.3f' % (x[i,0], y[i,0], results[i,0])) |
下面的示例演示了如何创建二维输入空间的均匀样本网格和目标函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 采样 2d 目标函数 from numpy import arange from numpy import meshgrid # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 总结一些输入域 print(x[:5, :5]) # 计算目标值 results = objective(x, y) # 总结一些结果 print(results[:5, :5]) # 创建一些输入到一些结果的映射 for i in range(5): print('f(%.3f, %.3f) = %.3f' % (x[i,0], y[i,0], results[i,0])) |
运行示例,首先总结网格中的一些点,然后是某些点的目标函数评估。
最后,我们列举二维输入空间中的坐标及其对应的函数评估。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
[[-5. -4.9 -4.8 -4.7 -4.6] [-5. -4.9 -4.8 -4.7 -4.6] [-5. -4.9 -4.8 -4.7 -4.6] [-5. -4.9 -4.8 -4.7 -4.6] [-5. -4.9 -4.8 -4.7 -4.6]] [[50. 49.01 48.04 47.09 46.16] [49.01 48.02 47.05 46.1 45.17] [48.04 47.05 46.08 45.13 44.2 ] [47.09 46.1 45.13 44.18 43.25] [46.16 45.17 44.2 43.25 42.32]] f(-5.000, -5.000) = 50.000 f(-5.000, -4.900) = 49.010 f(-5.000, -4.800) = 48.040 f(-5.000, -4.700) = 47.090 f(-5.000, -4.600) = 46.160 |
现在我们熟悉了如何对输入空间进行采样和评估点,让我们看看如何绘制函数。
测试函数等高线图
二维函数的流行绘图方法是等高线图。
此图创建了目标函数输出的平面表示,其中颜色和等高线指示目标函数输出的相对值或高度。
这就像地形图一样,可以区分山脉和山谷。
这可以使用 contour() Matplotlib 函数来实现,该函数直接接收网格和网格的评估作为输入。
然后,我们可以指定要绘制的等高线数量和要使用的颜色方案。在此示例中,我们将使用 50 个级别和流行的“jet”颜色方案,其中低级别使用冷色方案(蓝色),高级别使用暖色方案(红色)。
|
1 2 3 4 5 |
... # 创建一个具有 50 个级别和 jet 颜色方案的等高线图 pyplot.contour(x, y, results, 50, alpha=1.0, cmap='jet') # 显示绘图 pyplot.show() |
将这些内容汇总,创建二维目标函数等高线图的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# 创建一个具有 50 个级别和 jet 颜色方案的等高线图 pyplot.contour(x, y, results, 50, alpha=1.0, cmap='jet') # 显示绘图 pyplot.show() Tying this together, the complete example of creating a contour plot of the two-dimensional objective function is listed below. # 二维目标函数等高线图 from numpy import arange from numpy import meshgrid from matplotlib import pyplot # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 创建一个具有 50 个级别和 jet 颜色方案的等高线图 pyplot.contour(x, y, results, 50, alpha=1.0, cmap='jet') # 显示绘图 pyplot.show() |
运行示例,创建等高线图。
我们可以看到,曲面边缘附近更弯曲的部分有更多的等高线来显示细节,而中间部分不那么弯曲的部分则有较少的等高线。
我们可以看到,该域的最低点是中间,正如预期的那样。
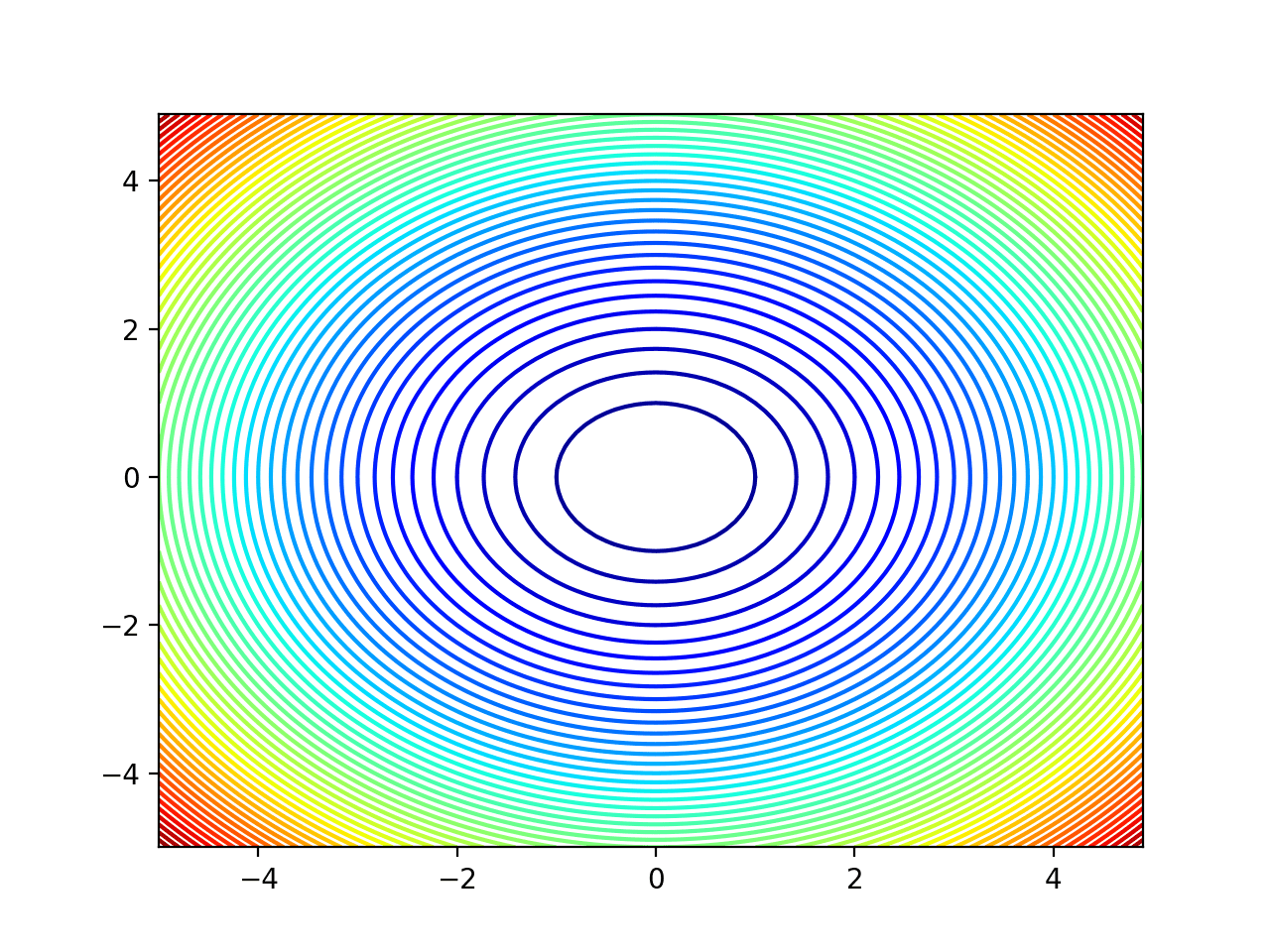
二维目标函数的等高线图
测试函数填充等高线图
用颜色填充等高线图以显示更完整的曲面也很有帮助。
同样,颜色只是简单的线性插值,不是真实的函数评估。在更复杂的函数上必须记住这一点,这些函数将不会显示精细的细节。
我们可以使用函数的 contourf() 版本来填充等高线图,它接受相同的参数。
|
1 2 3 |
... # 使用50个级别和jet颜色方案创建填充等高线图 pyplot.contourf(x, y, results, levels=50, cmap='jet') |
我们还可以在图上显示最优值,在此例中,用一个白色的星号表示,它会在图的最低部分(蓝色背景)上脱颖而出。
|
1 2 3 4 5 |
... # 定义已知函数的最优值 optima_x = [0.0, 0.0] # 将函数最优值绘制成白色星号 pyplot.plot([optima_x[0]], [optima_x[1]], '*', color='white') |
总而言之,下面列出了带有最优值标记的填充等高线图的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 2d 目标函数的填充等高线图并显示最优值 from numpy import arange from numpy import meshgrid from matplotlib import pyplot # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用50个级别和jet颜色方案创建填充等高线图 pyplot.contourf(x, y, results, levels=50, cmap='jet') # 定义已知函数的最优值 optima_x = [0.0, 0.0] # 将函数最优值绘制成白色星号 pyplot.plot([optima_x[0]], [optima_x[1]], '*', color='white') # 显示绘图 pyplot.show() |
运行该示例将创建填充等高线图,从而更好地了解目标函数的形状。
位于 [x=0, y=0] 的最优值随后用白色星号清晰标记。
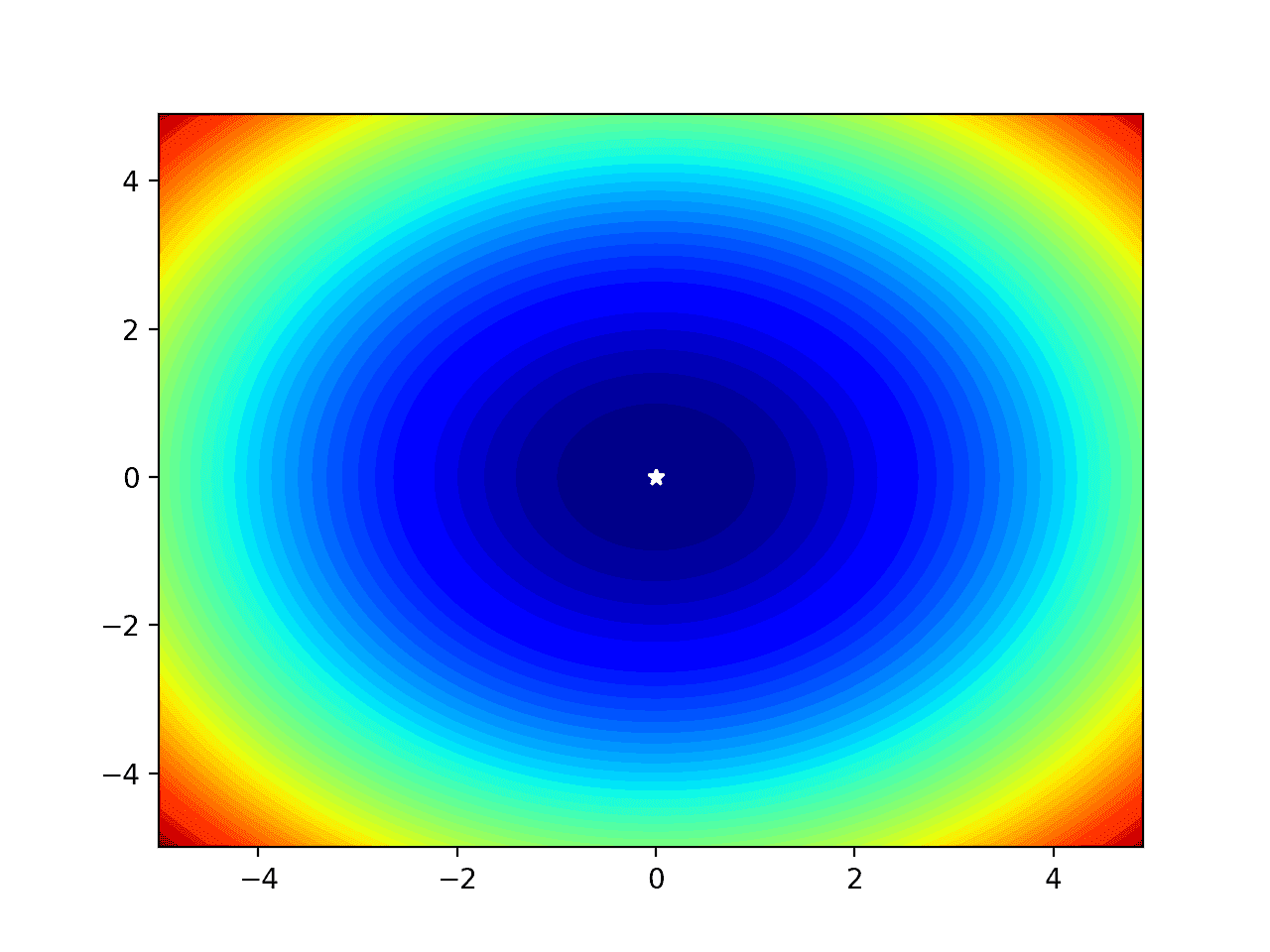
带有白色星号标记最优值的二维目标函数填充等高线图
带样本的测试函数填充等高线图
我们可能希望显示优化算法的进度,以了解其在目标函数形状背景下的行为。
在这种情况下,我们可以用输入空间中的随机坐标来模拟优化算法选择的点。
|
1 2 3 4 5 |
... # 模拟优化算法生成的样本 seed(1) sample_x = r_min + rand(10) * (r_max - r_min) sample_y = r_min + rand(10) * (r_max - r_min) |
然后可以将这些点直接绘制为黑圆圈,它们的上下文颜色可以提供关于其相对质量的 ধারণা。
|
1 2 3 |
... # 将样本绘制为黑色圆圈 pyplot.plot(sample_x, sample_y, 'o', color='black') |
总而言之,下面列出了绘制了最优值和输入样本的填充等高线图的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
# 2d 目标函数的填充等高线图并显示最优值和样本 from numpy import arange from numpy import meshgrid from numpy.random import seed from numpy.random import rand from matplotlib import pyplot # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 模拟优化算法生成的样本 seed(1) sample_x = r_min + rand(10) * (r_max - r_min) sample_y = r_min + rand(10) * (r_max - r_min) # 使用50个级别和jet颜色方案创建填充等高线图 pyplot.contourf(x, y, results, levels=50, cmap='jet') # 定义已知函数的最优值 optima_x = [0.0, 0.0] # 将函数最优值绘制成白色星号 pyplot.plot([optima_x[0]], [optima_x[1]], '*', color='white') # 将样本绘制为黑色圆圈 pyplot.plot(sample_x, sample_y, 'o', color='black') # 显示绘图 pyplot.show() |
运行该示例,我们可以看到与之前相同的填充等高线图,并标记了最优值。
现在我们可以看到样本以黑点显示,它们的周围颜色和与最优值的相对距离可以大致了解算法(此处为随机点)在解决问题上的接近程度。
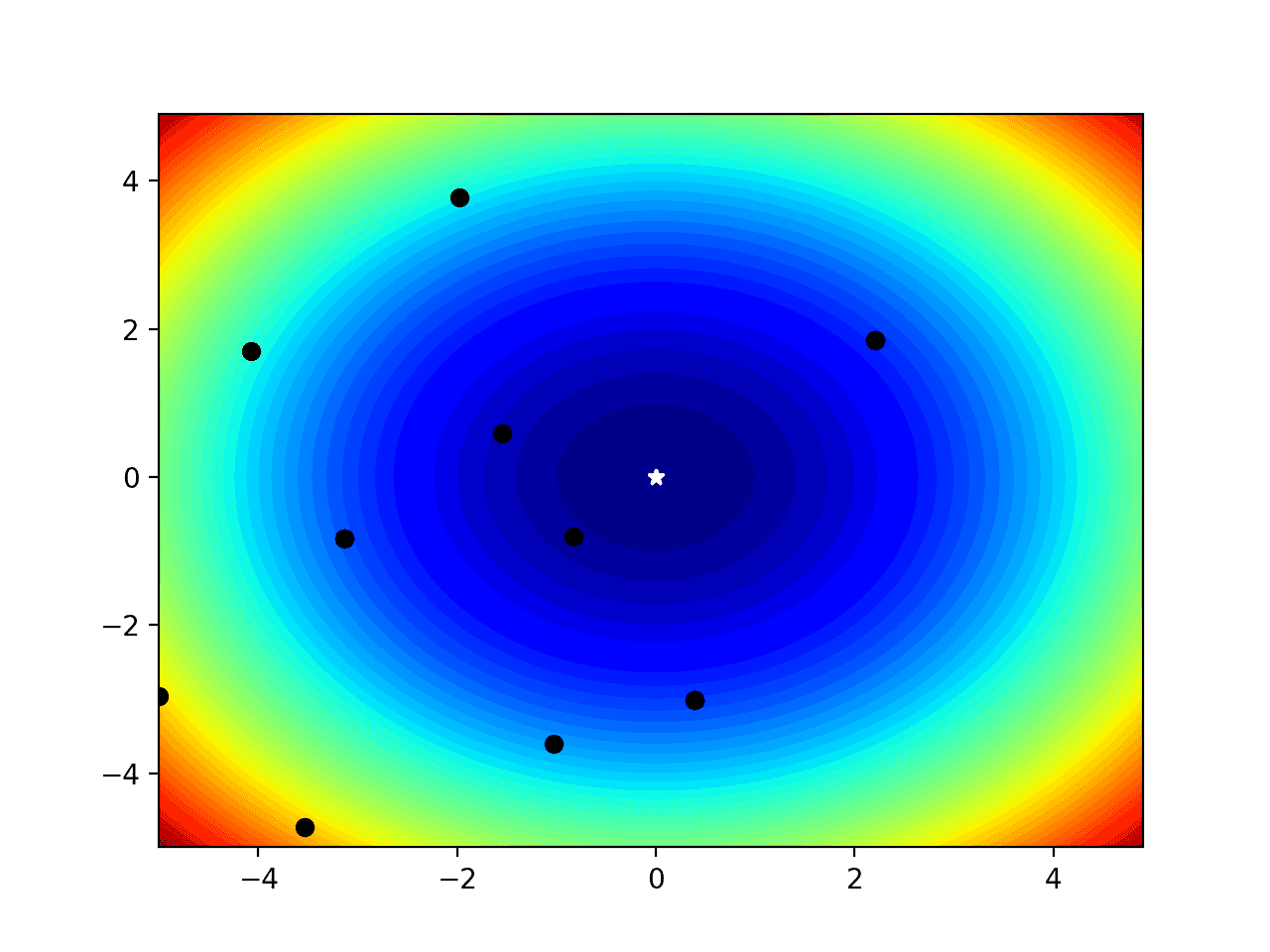
带有最优值和输入样本标记的二维目标函数填充等高线图
测试函数曲面图
最后,我们可能希望创建目标函数的 ثلاث-dimensional 图,以更全面地了解函数的曲率。
这可以通过 plot_surface() Matplotlib 函数 来实现,与等高线图一样,它直接接受网格和函数评估。
|
1 2 3 4 5 |
... # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') |
下面列出了创建曲面图的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# 2d 目标函数的曲面图 from numpy import arange from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
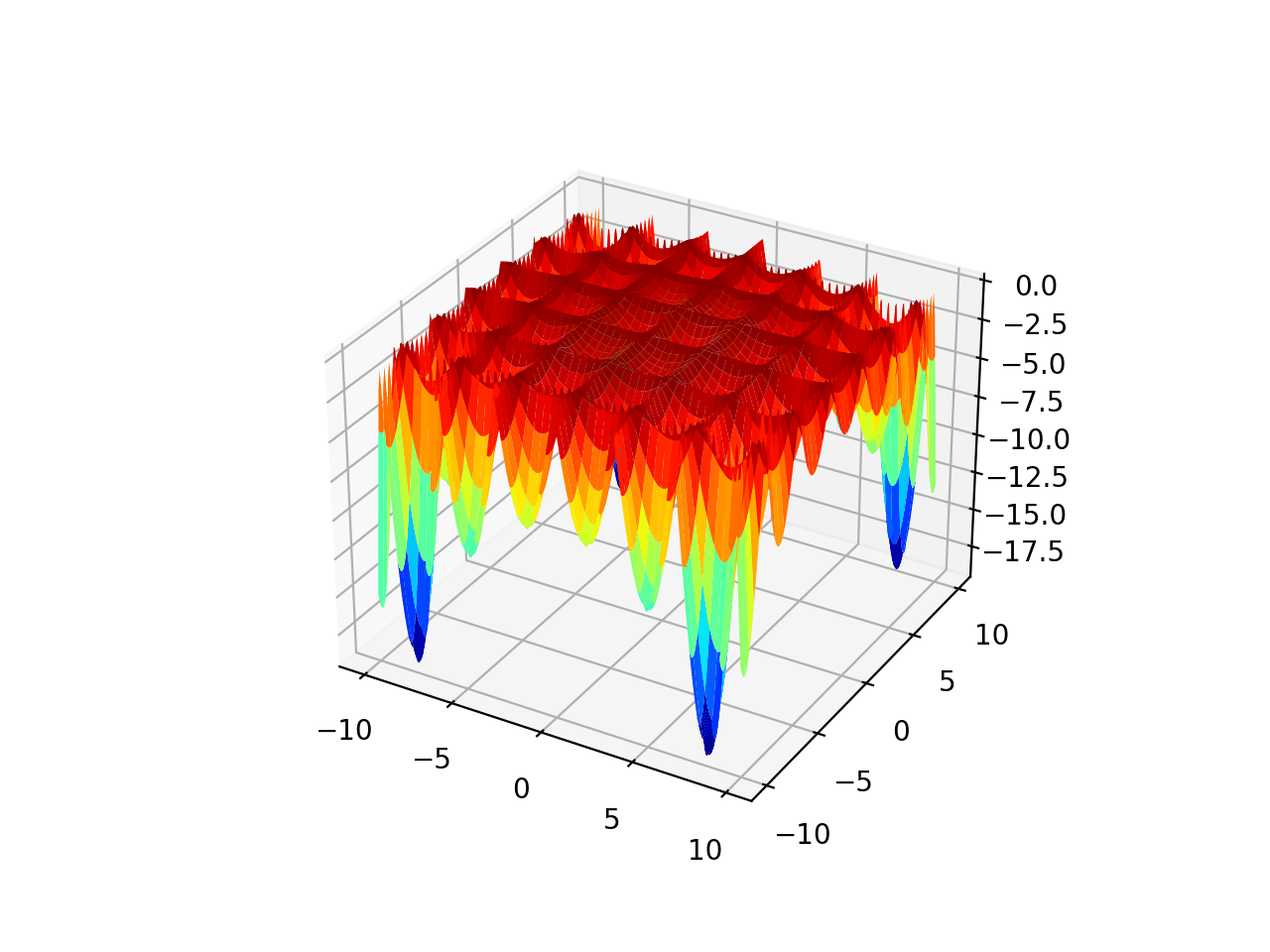
运行示例将创建目标函数的三维曲面图。
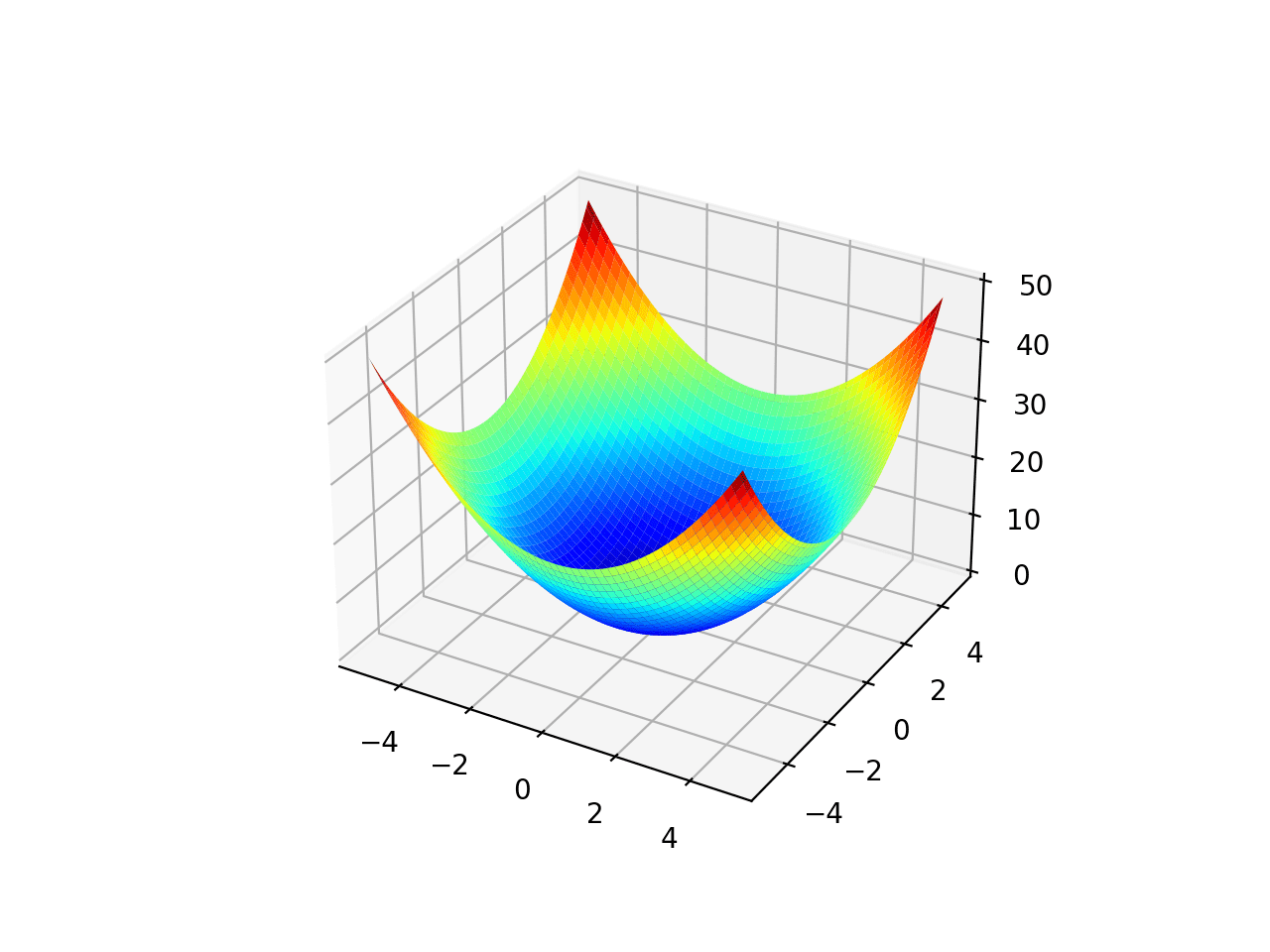
二维目标函数的曲面图
此外,该图是交互式的,这意味着您可以使用鼠标拖动曲面的视角,并从不同角度查看它。
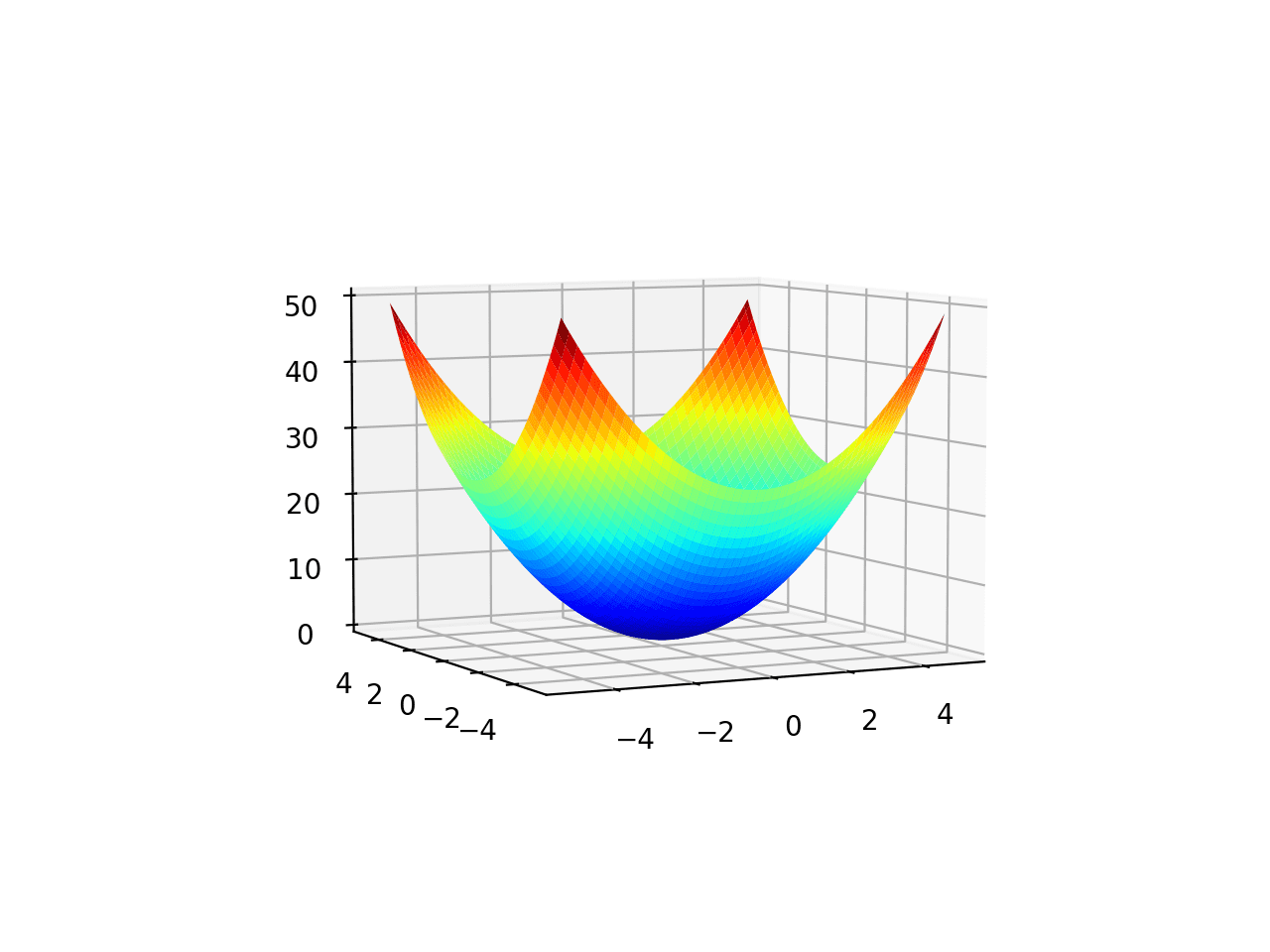
从不同角度查看的二维目标函数曲面图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
API
- 优化和根查找(scipy.optimize)
- 优化(scipy.optimize)
- numpy.meshgrid API.
- matplotlib.pyplot.contour API.
- matplotlib.pyplot.contourf API.
- mpl_toolkits.mplot3d.Axes3D.plot_surface API.
文章
总结
在本教程中,您学习了如何在 Python 中为函数优化创建可视化。
具体来说,你学到了:
- 可视化是研究函数优化算法时的重要工具。
- 如何使用折线图可视化一维函数和样本。
- 如何使用等高线图和曲面图可视化二维函数和样本。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



感谢 Jason 带来的富有洞察力的教程。期待您的优化教科书。您的书读起来总是很愉快。
谢谢!
感谢您带来一个非常有趣的教程。即使是初学者也容易理解。
写一个关于学习型优化器的教程是否可行?
https://arxiv.org/abs/2011.02159
感谢您的建议。
Jason,对测试函数的详细解释非常精彩。这个教程值得一读,对每个人都很有帮助。