时间序列回归问题上的预测误差被称为残差或残差误差。
仔细探索时间序列预测问题上的残差误差,可以告诉您很多关于您的预测模型的信息,甚至可以建议改进之处。
在本教程中,您将学习如何可视化时间序列预测的残差误差。
完成本教程后,您将了解:
- 如何创建和查看残差误差随时间变化的折线图。
- 如何查看残差图分布的汇总统计信息和图表。
- 如何探索残差误差的自相关结构。
开启您的项目,阅读我的新书《Python 时间序列预测入门》,其中包含分步教程和所有示例的Python 源代码文件。
让我们开始吧。
- 2019 年 4 月更新:更新了数据集链接。
- 2019年8月更新:更新了数据加载以使用新的API。
- 2019年9月更新:更新了使用最新API的示例。
残差预测误差
时间序列预测问题上的预测误差被称为残差误差或残差。
残差误差计算为期望结果减去预测值,例如:
|
1 |
残差误差 = 期望值 - 预测值 |
或者,更简洁地使用标准术语表示为:
|
1 |
e = y - yhat |
我们经常仅止于此,并通过汇总此误差来总结模型的技能。
相反,我们可以收集所有预测的个体残差误差,并利用它们来更好地理解预测模型。
通常,在探索残差误差时,我们会寻找模式或结构。模式的出现表明误差不是随机的。
我们期望残差误差是随机的,因为这意味着模型已经捕获了所有结构,而剩下的唯一误差是时间序列中无法建模的随机波动。
模式或结构的出现表明模型可以捕获并利用更多信息来做出更好的预测。
在我们开始探索查找残差误差模式的各种方法之前,我们需要一些背景信息。在下一节中,我们将使用一个数据集和一个简单的预测方法,用它们来生成残差误差,以便在本教程中进行探索。
停止以**慢速**学习时间序列预测!
参加我的免费7天电子邮件课程,了解如何入门(附带示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
每日女性出生数据集
此数据集描述了 1959 年加利福尼亚州每日女性出生人数。
单位是计数,有 365 个观测值。数据集来源为 Newton,1988。
下载数据集并将其放在您当前的工作目录中,文件名为“_daily-total-female-births.csv_”。
以下是从 CSV 加载“每日女性出生人数”数据集的示例。
|
1 2 3 4 5 6 |
from pandas import read_csv from matplotlib import pyplot series = read_csv('daily-total-female-births.csv', header=0, index_col=0) print(series.head()) series.plot() pyplot.show() |
运行示例将打印加载文件的前 5 行。
|
1 2 3 4 5 6 7 |
日期 1959-01-01 35 1959-01-02 32 1959-01-03 30 1959-01-04 31 1959-01-05 44 Name: Births, dtype: int64 |
数据集也显示为随时间变化的观测值的折线图。
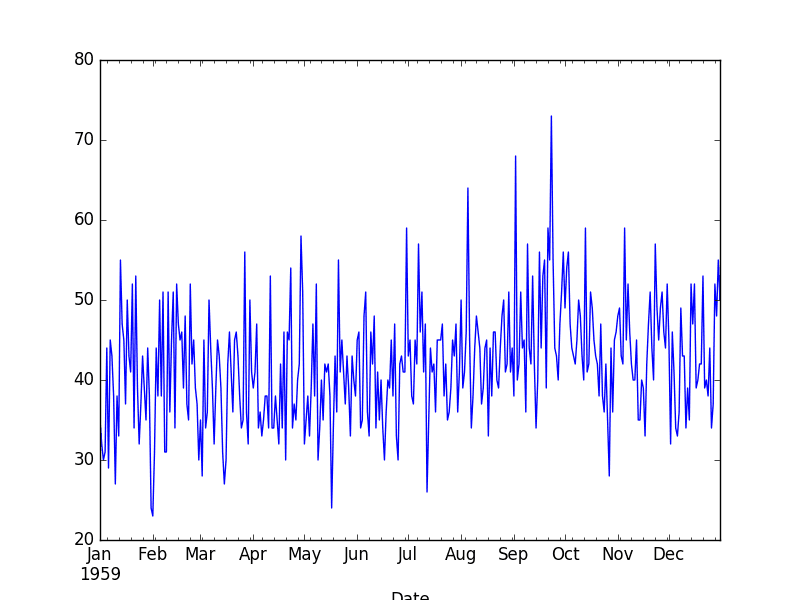
每日女性出生数据集
持续性预测模型
我们可以做出的最简单的预测是预测前一个时间步发生的事情将与下一个时间步发生的事情相同。
这被称为“朴素预测”或持续性预测模型。
我们可以在 Python 中实现持续性模型。
加载数据集后,它被转化为监督学习问题。创建了数据集的滞后版本,其中前一个时间步(t-1)用作输入变量,下一个时间步(t+1)用作输出变量。
|
1 2 3 4 |
# 创建滞后数据集 values = DataFrame(series.values) dataframe = concat([values.shift(1), values], axis=1) dataframe.columns = ['t-1', 't+1'] |
接下来,数据集被分割成训练集和测试集。总计 66% 的数据用于训练,其余 34% 用于测试集。持续性模型不需要训练;这只是一个标准的测试框架方法。
分割后,训练集和测试集被分离成它们的输入和输出分量。
|
1 2 3 4 5 6 |
# 拆分为训练集和测试集 X = dataframe.values train_size = int(len(X) * 0.66) train, test = X[1:train_size], X[train_size:] train_X, train_y = train[:,0], train[:,1] test_X, test_y = test[:,0], test[:,1] |
持续性模型通过将输出值(y)预测为输入值(x)的副本来实现。
|
1 2 |
# 持久性模型 predictions = [x for x in test_X] |
然后,残差误差计算为期望结果(test_y)与预测值(predictions)之间的差值。
|
1 2 |
# 计算残差 residuals = [test_y[i]-predictions[i] for i in range(len(predictions))] |
该示例将所有这些内容整合在一起,并为我们提供了一组残差预测误差,我们可以在本教程中进行探索。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
from pandas import read_csv from pandas import DataFrame 从 pandas 导入 concat series = read_csv('daily-total-female-births.csv', header=0, index_col=0) # 创建滞后数据集 values = DataFrame(series.values) dataframe = concat([values.shift(1), values], axis=1) dataframe.columns = ['t-1', 't+1'] # 拆分为训练集和测试集 X = dataframe.values train_size = int(len(X) * 0.66) train, test = X[1:train_size], X[train_size:] train_X, train_y = train[:,0], train[:,1] test_X, test_y = test[:,0], test[:,1] # 持久性模型 predictions = [x for x in test_X] # 计算残差 residuals = [test_y[i]-predictions[i] for i in range(len(predictions))] residuals = DataFrame(residuals) print(residuals.head()) |
运行示例将打印预测残差的前 5 行。
|
1 2 3 4 5 |
0 9.0 1 -10.0 2 3.0 3 -6.0 4 30.0 |
残差折线图
第一个图是查看残差预测误差随时间变化的折线图。
我们希望该图在 0 值附近随机波动,不显示任何趋势或周期性结构。
可以将残差误差数组包装在 Pandas DataFrame 中并直接绘图。下面的代码提供了一个示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
from pandas import read_csv from pandas import DataFrame 从 pandas 导入 concat from matplotlib import pyplot series = read_csv('daily-total-female-births.csv', header=0, index_col=0) # 创建滞后数据集 values = DataFrame(series.values) dataframe = concat([values.shift(1), values], axis=1) dataframe.columns = ['t-1', 't+1'] # 拆分为训练集和测试集 X = dataframe.values train_size = int(len(X) * 0.66) train, test = X[1:train_size], X[train_size:] train_X, train_y = train[:,0], train[:,1] test_X, test_y = test[:,0], test[:,1] # 持久性模型 predictions = [x for x in test_X] # 计算残差 residuals = [test_y[i]-predictions[i] for i in range(len(predictions))] residuals = DataFrame(residuals) # 绘制残差 residuals.plot() pyplot.show() |
运行示例显示了一个看似随机的残差时间序列图。
如果我们看到趋势、季节性或周期性结构,我们可以回到模型并尝试直接捕获这些元素。
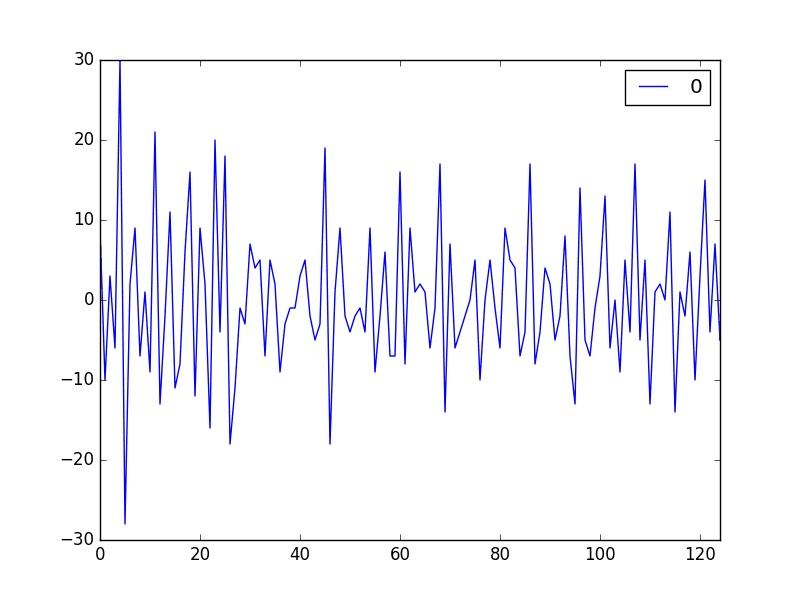
每日女性出生人数数据集的残差误差折线图
接下来,我们查看汇总统计信息,这些信息可用于了解误差如何在零周围分布。
残差汇总统计
我们可以计算残差误差的汇总统计信息。
主要我们关心的是残差误差的平均值。接近零的值表示预测没有偏差,而正值和负值表示预测存在正偏差或负偏差。
了解预测中的偏差很有用,因为可以在使用或评估预测之前直接对其进行校正。
下面是一个计算残差误差分布汇总统计信息的示例。这包括分布的均值和标准差,以及百分位数以及观察到的最小和最大误差。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
from pandas import read_csv from pandas import DataFrame 从 pandas 导入 concat from matplotlib import pyplot series = read_csv('daily-total-female-births.csv', header=0, index_col=0) # 创建滞后数据集 values = DataFrame(series.values) dataframe = concat([values.shift(1), values], axis=1) dataframe.columns = ['t-1', 't+1'] # 拆分为训练集和测试集 X = dataframe.values train_size = int(len(X) * 0.66) train, test = X[1:train_size], X[train_size:] train_X, train_y = train[:,0], train[:,1] test_X, test_y = test[:,0], test[:,1] # 持久性模型 predictions = [x for x in test_X] # 计算残差 residuals = [test_y[i]-predictions[i] for i in range(len(predictions))] residuals = DataFrame(residuals) # 汇总统计 print(residuals.describe()) |
运行示例显示平均误差值接近零,但可能还不够接近。
这表明可能存在一些偏差,我们可以通过执行偏差校正来进一步改进模型。这可以通过将平均残差误差 (0.064000) 添加到预测值中来实现。
在这种情况下,这可能有效,但它是一种朴素的偏差校正形式,并且有更复杂的可用方法。
|
1 2 3 4 5 6 7 8 |
count 125.000000 mean 0.064000 std 9.187776 min -28.000000 25% -6.000000 50% -1.000000 75% 5.000000 max 30.000000 |
接下来,我们超越汇总统计信息,研究可视化残差误差分布的方法。
残差直方图和密度图
图表可用于更好地理解超越汇总统计信息的误差分布。
我们期望预测误差呈正态分布,均值为零。
图表有助于发现此分布中的偏斜。
我们可以使用直方图和密度图来更好地理解残差误差的分布。下面的示例创建了每个图一个。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
from pandas import read_csv from pandas import DataFrame 从 pandas 导入 concat from matplotlib import pyplot series = read_csv('daily-total-female-births.csv', header=0, index_col=0) # 创建滞后数据集 values = DataFrame(series.values) dataframe = concat([values.shift(1), values], axis=1) dataframe.columns = ['t-1', 't+1'] # 拆分为训练集和测试集 X = dataframe.values train_size = int(len(X) * 0.66) train, test = X[1:train_size], X[train_size:] train_X, train_y = train[:,0], train[:,1] test_X, test_y = test[:,0], test[:,1] # 持久性模型 predictions = [(x-0.064000) for x in test_X] # 计算残差 residuals = [test_y[i]-predictions[i] for i in range(len(predictions))] residuals = DataFrame(residuals) # 直方图 residuals.hist() pyplot.show() # 密度图 residuals.plot(kind='kde') pyplot.show() |
我们可以看到分布具有高斯外观,但可能更尖锐,显示出具有一定不对称性的指数分布。
如果图显示出明显非高斯的分布,则表明建模过程中所做的假设可能不正确,并且可能需要不同的建模方法。
大的偏斜可能表明有机会在建模前对数据进行变换,例如取对数或平方根。
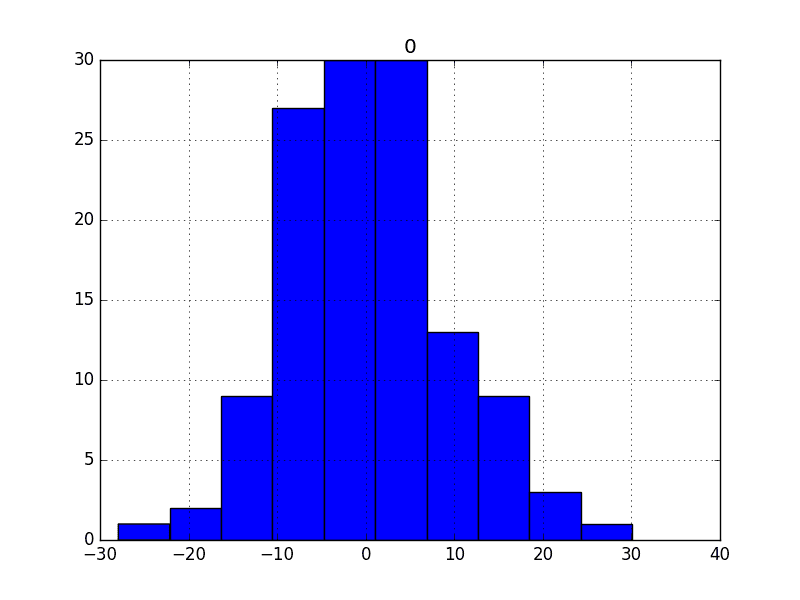
每日女性出生人数数据集的残差误差直方图
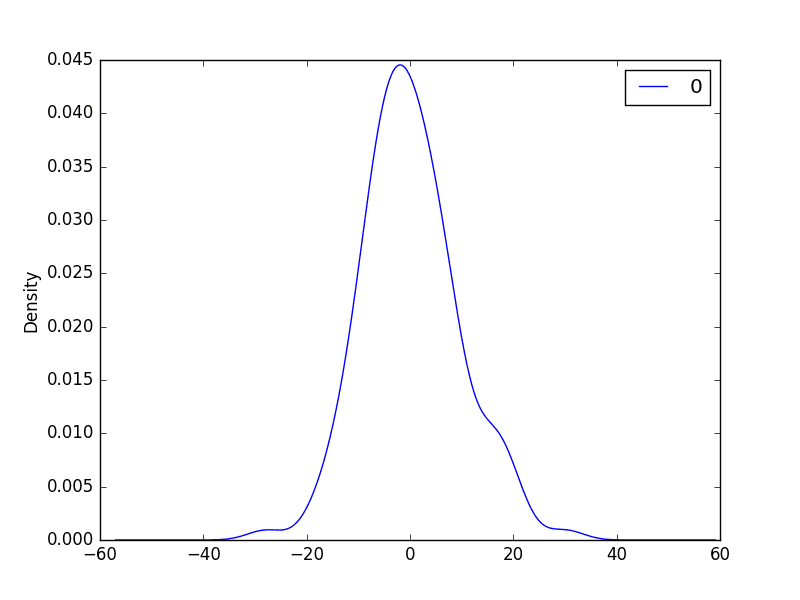
每日女性出生人数数据集的残差误差密度图
接下来,我们将研究另一种快速且可能更可靠的方法来检查残差分布是否为高斯分布。
残差 Q-Q 图
Q-Q 图,或分位数图,用于比较两个分布,并可以用来查看它们的相似程度或差异程度。
我们可以使用 statsmodels 库中的 qqplot() 函数创建 Q-Q 图。
Q-Q 图可用于快速检查残差误差分布的正态性。
这些值被排序并与理想的高斯分布进行比较。比较显示为散点图(x 轴为理论值,y 轴为观测值),其中两个分布的匹配显示为从左下到右上的对角线。
该图有助于发现与此预期明显不同的地方。
下面是残差误差 Q-Q 图的示例。x 轴显示理论分位数,y 轴显示样本分位数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
from pandas import read_csv from pandas import DataFrame 从 pandas 导入 concat from matplotlib import pyplot import numpy from statsmodels.graphics.gofplots import qqplot series = read_csv('daily-total-female-births.csv', header=0, index_col=0) # 创建滞后数据集 values = DataFrame(series.values) dataframe = concat([values.shift(1), values], axis=1) dataframe.columns = ['t-1', 't+1'] # 拆分为训练集和测试集 X = dataframe.values train_size = int(len(X) * 0.66) train, test = X[1:train_size], X[train_size:] train_X, train_y = train[:,0], train[:,1] test_X, test_y = test[:,0], test[:,1] # 持久性模型 predictions = [(x-0.064000) for x in test_X] # 计算残差 residuals = [test_y[i]-predictions[i] for i in range(len(predictions))] residuals = numpy.array(residuals) qqplot(residuals) pyplot.show() |
运行示例显示了一个 Q-Q 图,该图表明分布看似呈正态,但有一些起伏和异常值。
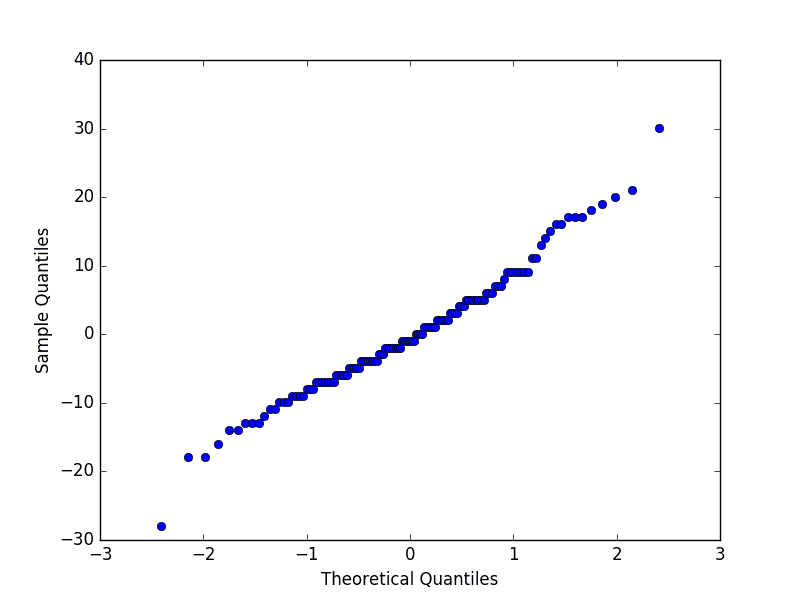
每日女性出生人数数据集的残差误差 Q-Q 图
接下来,我们可以检查误差之间随时间变化的自相关性。
残差自相关图
自相关计算观测值与先前时间步的观测值之间的关系强度。
我们可以计算残差误差时间序列的自相关性并绘制结果。这被称为自相关图。
我们不希望残差之间存在任何自相关。这将通过自相关分数低于显著性阈值(图上的虚线和点划线水平线)来显示。
残差图中存在显著的自相关性表明,模型可以更好地结合观测值与滞后观测值之间的关系,这称为自回归。
Pandas 提供了一个用于计算自相关图的内置函数,名为 autocorrelation_plot()。
下面是可视化残差误差自相关性的示例。x 轴显示滞后,y 轴显示观测值与滞后变量之间的相关性,其中相关性值在 -1 到 1 之间,分别表示负相关和正相关。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
from pandas import read_csv from pandas import DataFrame 从 pandas 导入 concat from matplotlib import pyplot from pandas.plotting import autocorrelation_plot series = read_csv('daily-total-female-births.csv', header=0, index_col=0) # 创建滞后数据集 values = DataFrame(series.values) dataframe = concat([values.shift(1), values], axis=1) dataframe.columns = ['t-1', 't+1'] # 拆分为训练集和测试集 X = dataframe.values train_size = int(len(X) * 0.66) train, test = X[1:train_size], X[train_size:] train_X, train_y = train[:,0], train[:,1] test_X, test_y = test[:,0], test[:,1] # 持久性模型 predictions = [x for x in test_X] # 计算残差 residuals = [test_y[i]-predictions[i] for i in range(len(predictions))] residuals = DataFrame(residuals) autocorrelation_plot(residuals) pyplot.show() |
运行示例会创建其他残差误差的自回归图。
我们在整个图中看不到明显的自相关趋势。在滞后 7 处可能存在一些值得进一步调查的积极自相关,该自相关似乎是显著的。
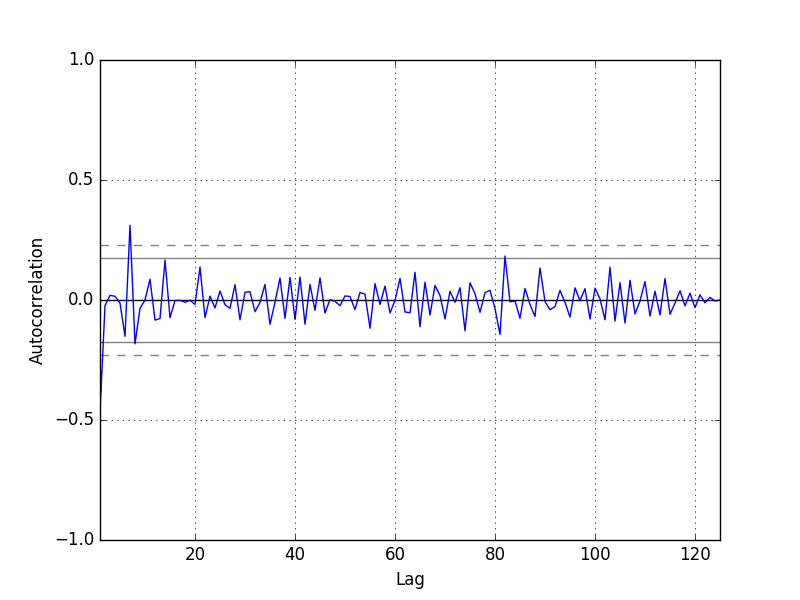
每日女性出生人数数据集的残差误差自相关图
总结
在本教程中,您学习了如何使用 Python 探索残差预测误差的时间序列。
具体来说,你学到了:
- 如何将预测残差误差的时间序列绘制为折线图。
- 如何使用统计信息、密度图和 Q-Q 图来探索残差误差的分布。
- 如何检查残差时间序列的自相关性。
您对探索残差误差时间序列或本教程有任何疑问吗?
请在下面的评论中提出您的问题。





很棒的教程,但请更改
from pandas.tools.plotting import autocorrelation_plot
为
from pandas.plotting import autocorrelation_plot
因为在较新版本的 pandas 中,路径已更改。
感谢 Anton 的提示。
这是一篇很棒的文章。
代码更改:pandas.tools.plotting 已移至 pandas.plotting,因此下面的命令在您的代码中不起作用。
from pandas.tools.plotting import autocorrelation_plot
谢谢。
非常感谢,Jason。
实际上对我的研究很有帮助。很棒的资料!
不客气,我很高兴它有帮助。
你好,Jason!
我得到一个具有拉普拉斯分布的残差直方图。可能是什么原因?或者我该如何解释?
也许有更多数据会变成高斯分布,或者可能足够接近高斯分布。
否则,也许可以尝试在建模之前对输入数据进行幂变换。
太棒了,我们能否找到两个序列的残差和相关性,一个是系统的输出,另一个是估计的模型,而无需找到模型?有可能吗?
你的意思是你们已经有了这两个序列?如果是,是的,您可以直接运行相关函数,将这两个序列作为输入。