梯度消失问题的可视化

作者： Adrian Tam 发布于 2021年11月26日分类：深度学习性能 15

深度学习是最近的一项发明。部分原因是计算能力的提高，使我们能够在神经网络中使用更多感知器层。但与此同时，只有在我们知道如何解决梯度消失问题之后，才能训练深度网络。

在本教程中，我们将直观地研究梯度消失问题存在的原因。

完成本教程后，您将了解：

什么是梯度消失
哪种神经网络配置容易出现梯度消失
如何在 Keras 中运行手动训练循环
如何从 Keras 模型中提取权重和梯度

让我们开始吧

Visualizing the vanishing gradient problem

梯度消失问题的可视化
照片由 Alisa Anton 拍摄，保留部分权利。

教程概述

本教程分为5个部分，它们是：

多层感知器模型的配置
梯度消失问题的示例
查看每一层的权重
查看每一层的梯度
Glorot 初始化

多层感知器模型的配置

由于神经网络是通过梯度下降进行训练的，人们认为激活函数必须是可微函数才能在神经网络中使用。这导致我们传统上使用 Sigmoid 函数或双曲正切作为激活函数。

对于二分类问题，如果我们要进行逻辑回归，使 0 和 1 成为理想输出，则首选 Sigmoid 函数，因为它在此范围内
$$
\sigma(x) = \frac{1}{1+e^{-x}}
$$
如果我们需要在输出层进行 Sigmoid 激活，那么在神经网络的所有层中使用它也是很自然的。此外，神经网络中的每一层都有一个权重参数。最初，权重必须随机化，我们自然会使用一些简单的方法来完成，例如使用均匀随机分布或正态分布。

梯度消失问题的示例

为了说明梯度消失问题，我们尝试一个示例。神经网络是非线性函数。因此，它应该最适合非线性数据集的分类。我们使用 scikit-learn 的 `make_circle()` 函数来生成一些数据

from sklearn.datasets import make_circles
import matplotlib.pyplot as plt

# Make data: Two circles on x-y plane as a classification problem
X, y = make_circles(n_samples=1000, factor=0.5, noise=0.1)

plt.figure(figsize=(8,6))
plt.scatter(X[:,0], X[:,1], c=y)
plt.show()

from sklearn.datasets import make_circles

import matplotlib.pyplot as plt

# 制作数据：xy 平面上的两个圆圈作为分类问题

X, y = make_circles(n_samples=1000, factor=0.5, noise=0.1)

plt.figure(figsize=(8,6))

plt.scatter(X[:,0], X[:,1], c=y)

plt.show()

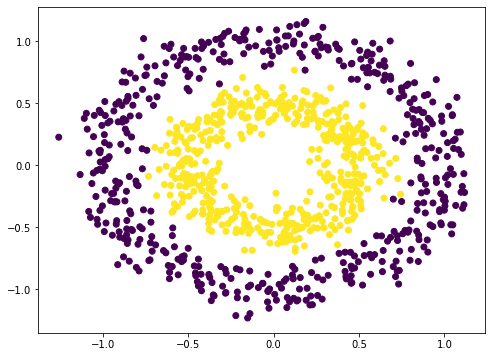
这并不难分类。一种朴素的方法是构建一个 3 层神经网络，它可以给出相当不错的结果

from tensorflow.keras.layers import Dense, Input
from tensorflow.keras import Sequential

model = Sequential([
    Input(shape=(2,)),
    Dense(5, "relu"),
    Dense(1, "sigmoid")
])
model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])
model.fit(X, y, batch_size=32, epochs=100, verbose=0)
print(model.evaluate(X,y))

from tensorflow.keras.layers import Dense, Input

from tensorflow.keras import Sequential

model = Sequential([

Input(shape=(2,)),

Dense(5, "relu"),

Dense(1, "sigmoid")

])

model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])

model.fit(X, y, batch_size=32, epochs=100, verbose=0)

print(model.evaluate(X,y))

32/32 [==============================] - 0s 1ms/step - loss: 0.2404 - acc: 0.9730
[0.24042171239852905, 0.9729999899864197]

1 2	32/32 [==============================] - 0s 1ms/step - loss: 0.2404 - acc: 0.9730 [0.24042171239852905, 0.9729999899864197]

注意，我们在上面的隐藏层中使用了修正线性单元 (ReLU)。默认情况下，Keras 中的密集层将使用线性激活（即无激活），这大多无用。我们通常在现代神经网络中使用 ReLU。但我们也可以尝试二十年前每个人都使用的老式方法

model = Sequential([
    Input(shape=(2,)),
    Dense(5, "sigmoid"),
    Dense(1, "sigmoid")
])
model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])
model.fit(X, y, batch_size=32, epochs=100, verbose=0)
print(model.evaluate(X,y))

model = Sequential([

Input(shape=(2,)),

Dense(5, "sigmoid"),

Dense(1, "sigmoid")

])

model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])

model.fit(X, y, batch_size=32, epochs=100, verbose=0)

print(model.evaluate(X,y))

32/32 [==============================] - 0s 1ms/step - loss: 0.6927 - acc: 0.6540
[0.6926590800285339, 0.6539999842643738]

1 2	32/32 [==============================] - 0s 1ms/step - loss: 0.6927 - acc: 0.6540 [0.6926590800285339, 0.6539999842643738]

准确性差得多。事实证明，通过增加更多层（至少在我的实验中）情况甚至更糟

model = Sequential([
    Input(shape=(2,)),
    Dense(5, "sigmoid"),
    Dense(5, "sigmoid"),
    Dense(5, "sigmoid"),
    Dense(1, "sigmoid")
])
model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])
model.fit(X, y, batch_size=32, epochs=100, verbose=0)
print(model.evaluate(X,y))

model = Sequential([

Input(shape=(2,)),

Dense(5, "sigmoid"),

Dense(1, "sigmoid")

])

model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])

model.fit(X, y, batch_size=32, epochs=100, verbose=0)

print(model.evaluate(X,y))

32/32 [==============================] - 0s 1ms/step - loss: 0.6922 - acc: 0.5330
[0.6921834349632263, 0.5329999923706055]

1 2	32/32 [==============================] - 0s 1ms/step - loss: 0.6922 - acc: 0.5330 [0.6921834349632263, 0.5329999923706055]

您的结果可能会因训练算法的随机性而异。您可能会看到 5 层 sigmoid 网络比 3 层网络表现差得多，或者没有。但这里的想法是，您无法像使用修正线性单元激活那样，仅仅通过增加层数就获得高准确率。

查看每一层的权重

我们难道不应该通过增加更多层来获得更强大的神经网络吗？

是的，应该如此。但事实证明，随着我们增加更多层，我们触发了梯度消失问题。为了说明发生了什么，让我们看看随着我们训练网络，权重是如何变化的。

在 Keras 中，我们允许将回调函数插入到训练过程中。我们将创建自己的回调对象，以便在每个 epoch 结束时拦截并记录多层感知器 (MLP) 模型的每一层的权重。

from tensorflow.keras.callbacks import Callback

class WeightCapture(Callback):
    "Capture the weights of each layer of the model"
    def __init__(self, model):
        super().__init__()
        self.model = model
        self.weights = []
        self.epochs = []

    def on_epoch_end(self, epoch, logs=None):
        self.epochs.append(epoch) # remember the epoch axis
        weight = {}
        for layer in model.layers:
            if not layer.weights:
                continue
            name = layer.weights[0].name.split("/")[0]
            weight[name] = layer.weights[0].numpy()
        self.weights.append(weight)

from tensorflow.keras.callbacks import Callback

class WeightCapture(Callback):

"捕获模型每一层的权重"

def __init__(self, model):

super().__init__()

self.model = model

self.weights = []

self.epochs = []

def on_epoch_end(self, epoch, logs=None):

self.epochs.append(epoch) # 记住 epoch 轴

weight = {}

for layer in model.layers:

if not layer.weights:

continue

name = layer.weights[0].name.split("/")[0]

weight[name] = layer.weights[0].numpy()

self.weights.append(weight)

我们派生 `Callback` 类并定义 `on_epoch_end()` 函数。这个类需要创建的模型来初始化。在每个 epoch 结束时，它将读取每个层并将权重保存到 numpy 数组中。

为了方便实验不同的 MLP 创建方法，我们创建了一个辅助函数来设置神经网络模型

def make_mlp(activation, initializer, name):
    "Create a model with specified activation and initalizer"
    model = Sequential([
        Input(shape=(2,), name=name+"0"),
        Dense(5, activation=activation, kernel_initializer=initializer, name=name+"1"),
        Dense(5, activation=activation, kernel_initializer=initializer, name=name+"2"),
        Dense(5, activation=activation, kernel_initializer=initializer, name=name+"3"),
        Dense(5, activation=activation, kernel_initializer=initializer, name=name+"4"),
        Dense(1, activation="sigmoid", kernel_initializer=initializer, name=name+"5")
    ])
    return model

def make_mlp(activation, initializer, name):

"使用指定的激活函数和初始化器创建模型"

model = Sequential([

Input(shape=(2,), name=name+"0"),

Dense(5, activation=activation, kernel_initializer=initializer, name=name+"1"),

Dense(5, activation=activation, kernel_initializer=initializer, name=name+"2"),

Dense(5, activation=activation, kernel_initializer=initializer, name=name+"3"),

Dense(5, activation=activation, kernel_initializer=initializer, name=name+"4"),

Dense(1, activation="sigmoid", kernel_initializer=initializer, name=name+"5")

])

return model

我们特意创建了一个包含 4 个隐藏层的神经网络，以便我们能看到每个层如何响应训练。我们将改变每个隐藏层的激活函数以及权重初始化。为了更容易区分，我们将为每个层命名，而不是让 Keras 分配名称。输入是 xy 平面上的一个坐标，因此输入形状是一个包含 2 个元素的向量。输出是二分类。因此，我们使用 Sigmoid 激活函数使输出落在 0 到 1 的范围内。

然后我们可以 `compile()` 模型以提供评估指标，并在 `fit()` 调用中传递回调以训练模型

initializer = RandomNormal(mean=0.0, stddev=1.0)
batch_size = 32
n_epochs = 100

model = make_mlp("sigmoid", initializer, "sigmoid")
capture_cb = WeightCapture(model)
capture_cb.on_epoch_end(-1)
model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])
model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=1)

initializer = RandomNormal(mean=0.0, stddev=1.0)

batch_size = 32

n_epochs = 100

model = make_mlp("sigmoid", initializer, "sigmoid")

capture_cb = WeightCapture(model)

capture_cb.on_epoch_end(-1)

model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])

model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=1)

在这里，我们首先调用 `make_mlp()` 创建神经网络。然后我们设置我们的回调对象。由于神经网络中每一层的权重在创建时就已经初始化，我们特意调用回调函数来记住它们的初始值。然后我们像往常一样从模型中调用 `compile()` 和 `fit()`，并提供回调对象。

模型拟合后，我们可以使用整个数据集进行评估

...
print(model.evaluate(X,y))

1 2	... print(model.evaluate(X,y))

[0.6649572253227234, 0.5879999995231628]

1	[0.6649572253227234, 0.5879999995231628]

这里的意思是，对于所有层都使用 sigmoid 激活的这个模型，对数损失为 0.665，准确率为 0.588。

我们可以进一步研究的是权重在训练迭代中的行为。除第一层和最后一层外，所有层的权重都是 5×5 矩阵。我们可以检查权重的平均值和标准差，以了解权重的样子

def plotweight(capture_cb):
    "Plot the weights' mean and s.d. across epochs"
    fig, ax = plt.subplots(2, 1, sharex=True, constrained_layout=True, figsize=(8, 10))
    ax[0].set_title("Mean weight")
    for key in capture_cb.weights[0]:
        ax[0].plot(capture_cb.epochs, [w[key].mean() for w in capture_cb.weights], label=key)
    ax[0].legend()
    ax[1].set_title("S.D.")
    for key in capture_cb.weights[0]:
        ax[1].plot(capture_cb.epochs, [w[key].std() for w in capture_cb.weights], label=key)
    ax[1].legend()
    plt.show()
    
plotweight(capture_cb)

def plotweight(capture_cb):

"绘制权重在各个 epoch 中的平均值和标准差"

fig, ax = plt.subplots(2, 1, sharex=True, constrained_layout=True, figsize=(8, 10))

ax[0].set_title("权重均值")

for key in capture_cb.weights[0]:

ax[0].plot(capture_cb.epochs, [w[key].mean() for w in capture_cb.weights], label=key)

ax[0].legend()

ax[1].set_title("标准差")

for key in capture_cb.weights[0]:

ax[1].plot(capture_cb.epochs, [w[key].std() for w in capture_cb.weights], label=key)

ax[1].legend()

plt.show()

plotweight(capture_cb)

这产生了以下图形：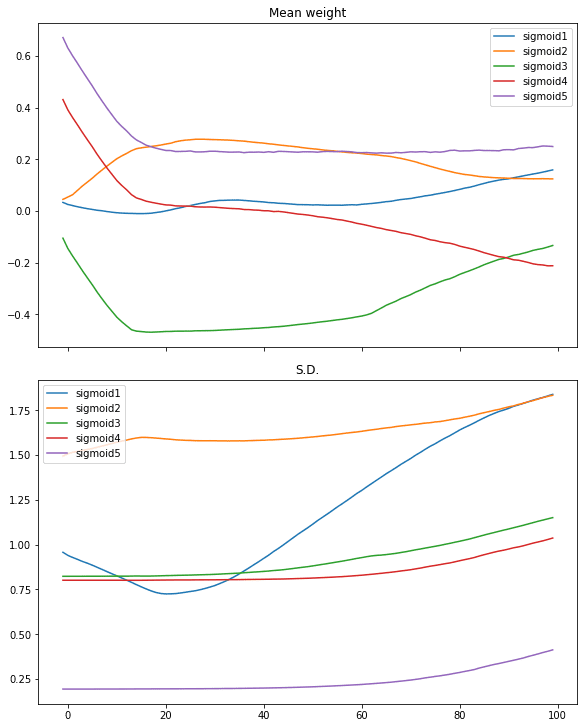

我们看到平均权重只在前 10 次迭代左右迅速移动。只有第一层的权重随着其标准差的增加而变得更加多样化。

我们可以使用双曲正切 (tanh) 激活函数重新启动相同的过程

# tanh activation, large variance gaussian initialization
model = make_mlp("tanh", initializer, "tanh")
capture_cb = WeightCapture(model)
capture_cb.on_epoch_end(-1)
model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])
model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=0)
print(model.evaluate(X,y))
plotweight(capture_cb)

# tanh 激活，大方差高斯初始化

model = make_mlp("tanh", initializer, "tanh")

capture_cb = WeightCapture(model)

capture_cb.on_epoch_end(-1)

model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])

model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=0)

print(model.evaluate(X,y))

plotweight(capture_cb)

[0.012918001972138882, 0.9929999709129333]

1	[0.012918001972138882, 0.9929999709129333]

对数损失和准确率都得到了改善。如果我们看图，我们没有看到权重平均值和标准差的突然变化，相反，所有层都缓慢收敛。

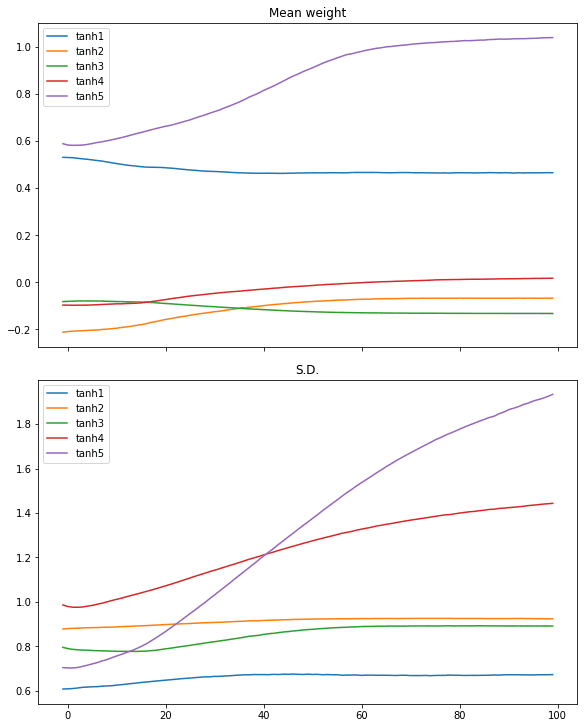
在 ReLU 激活中可以看到类似的情况

# relu activation, large variance gaussian initialization
model = make_mlp("relu", initializer, "relu")
capture_cb = WeightCapture(model)
capture_cb.on_epoch_end(-1)
model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])
model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=0)
print(model.evaluate(X,y))
plotweight(capture_cb)

# relu 激活，大方差高斯初始化

model = make_mlp("relu", initializer, "relu")

capture_cb = WeightCapture(model)

capture_cb.on_epoch_end(-1)

model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])

model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=0)

print(model.evaluate(X,y))

plotweight(capture_cb)

[0.016895903274416924, 0.9940000176429749]

1	[0.016895903274416924, 0.9940000176429749]

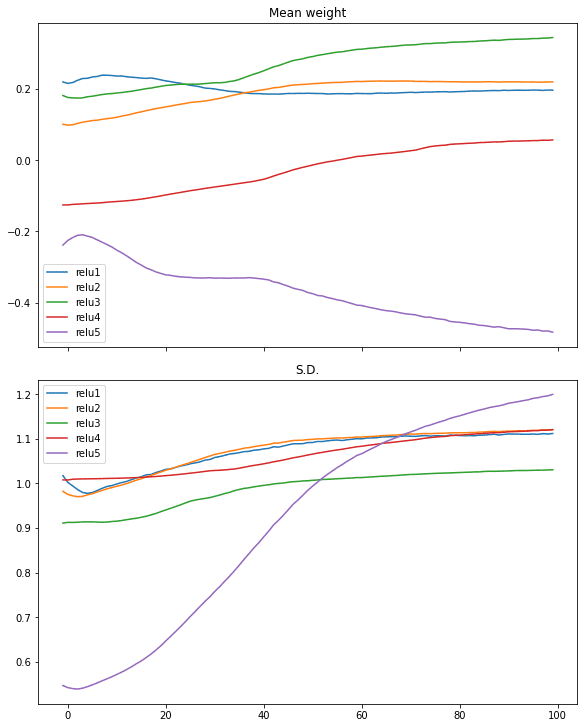
查看每一层的梯度

我们在上面看到了不同激活函数的效果。但实际上，重要的是梯度，因为我们在训练过程中运行梯度下降。Xavier Glorot 和 Yoshua Bengio 的论文“理解训练深度前馈神经网络的难度”建议查看每个训练迭代中每个层的梯度以及其标准差。

布拉德利 (2009) 发现，在初始化之后，从输出层向输入层移动时，反向传播的梯度会变小。他研究了每层都具有线性激活的神经网络，发现反向传播梯度的方差随着我们在网络中向后移动而减小

——《理解训练深度前馈神经网络的难度》（2010）

为了理解激活函数与训练过程中感知的梯度之间的关系，我们需要手动运行训练循环。

在 Tensorflow-Keras 中，可以通过开启梯度带（gradient tape）来运行训练循环，然后使神经网络模型产生输出，之后我们可以通过梯度带的自动微分获得梯度。随后，我们可以根据梯度下降更新规则更新参数（权重和偏差）。

因为在这个循环中可以很容易地获得梯度，所以我们可以复制一份。以下是我们如何实现训练循环，同时保留一份梯度副本的方法

optimizer = tf.keras.optimizers.RMSprop()
loss_fn = tf.keras.losses.BinaryCrossentropy()

def train_model(X, y, model, n_epochs=n_epochs, batch_size=batch_size):
    "Run training loop manually"
    train_dataset = tf.data.Dataset.from_tensor_slices((X, y))
    train_dataset = train_dataset.shuffle(buffer_size=1024).batch(batch_size)

    gradhistory = []
    losshistory = []
    def recordweight():
        data = {}
        for g,w in zip(grads, model.trainable_weights):
            if '/kernel:' not in w.name:
                continue # skip bias
            name = w.name.split("/")[0]
            data[name] = g.numpy()
        gradhistory.append(data)
        losshistory.append(loss_value.numpy())
    for epoch in range(n_epochs):
        for step, (x_batch_train, y_batch_train) in enumerate(train_dataset):
            with tf.GradientTape() as tape:
                y_pred = model(x_batch_train, training=True)
                loss_value = loss_fn(y_batch_train, y_pred)

            grads = tape.gradient(loss_value, model.trainable_weights)
            optimizer.apply_gradients(zip(grads, model.trainable_weights))

            if step == 0:
                recordweight()
    # After all epochs, record again
    recordweight()
    return gradhistory, losshistory

optimizer = tf.keras.optimizers.RMSprop()

loss_fn = tf.keras.losses.BinaryCrossentropy()

def train_model(X, y, model, n_epochs=n_epochs, batch_size=batch_size):

"手动运行训练循环"

train_dataset = tf.data.Dataset.from_tensor_slices((X, y))

train_dataset = train_dataset.shuffle(buffer_size=1024).batch(batch_size)

gradhistory = []

losshistory = []

def recordweight():

data = {}

for g,w in zip(grads, model.trainable_weights):

if '/kernel:' not in w.name:

continue # 跳过偏差

name = w.name.split("/")[0]

data[name] = g.numpy()

gradhistory.append(data)

losshistory.append(loss_value.numpy())

for epoch in range(n_epochs):

for step, (x_batch_train, y_batch_train) in enumerate(train_dataset):

with tf.GradientTape() as tape:

y_pred = model(x_batch_train, training=True)

loss_value = loss_fn(y_batch_train, y_pred)

grads = tape.gradient(loss_value, model.trainable_weights)

optimizer.apply_gradients(zip(grads, model.trainable_weights))

if step == 0:

recordweight()

# 所有 epoch 结束后，再次记录

recordweight()

return gradhistory, losshistory

上述函数中的关键是嵌套的 for 循环。在该循环中，我们启动 `tf.GradientTape()` 并将一批数据传递给模型以获得预测，然后使用损失函数进行评估。之后，我们可以通过比较损失与模型中可训练权重来从梯度带中提取梯度。接下来，我们使用优化器更新权重，优化器将隐式处理梯度下降算法中的学习权重和动量。

回顾一下，这里的梯度意味着以下内容。对于计算出的损失值 $L$ 和具有权重 $W=[w_1, w_2, w_3, w_4, w_5]$ 的层（例如，在输出层），则梯度是矩阵

$$
\frac{\partial L}{\partial W} = \Big[\frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, \frac{\partial L}{\partial w_3}, \frac{\partial L}{\partial w_4}, \frac{\partial L}{\partial w_5}\Big]
$$

但在开始下一次训练迭代之前，我们有机会进一步操作梯度：我们将梯度与权重匹配，以获取每个梯度的名称，然后将梯度副本保存为 numpy 数组。我们每个 epoch 只采样一次权重和损失，但您可以将其更改为以更高的频率采样。

有了这些，我们就可以绘制不同 epoch 的梯度。接下来，我们创建模型（但不调用 `compile()`，因为我们之后不会调用 `fit()`）并运行手动训练循环，然后绘制梯度以及梯度的标准差

from sklearn.metrics import accuracy_score

def plot_gradient(gradhistory, losshistory):
    "Plot gradient mean and sd across epochs"
    fig, ax = plt.subplots(3, 1, sharex=True, constrained_layout=True, figsize=(8, 12))
    ax[0].set_title("Mean gradient")
    for key in gradhistory[0]:
        ax[0].plot(range(len(gradhistory)), [w[key].mean() for w in gradhistory], label=key)
    ax[0].legend()
    ax[1].set_title("S.D.")
    for key in gradhistory[0]:
        ax[1].semilogy(range(len(gradhistory)), [w[key].std() for w in gradhistory], label=key)
    ax[1].legend()
    ax[2].set_title("Loss")
    ax[2].plot(range(len(losshistory)), losshistory)
    plt.show()

model = make_mlp("sigmoid", initializer, "sigmoid")
print("Before training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
gradhistory, losshistory = train_model(X, y, model)
print("After training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
plot_gradient(gradhistory, losshistory)

from sklearn.metrics import accuracy_score

def plot_gradient(gradhistory, losshistory):

"绘制梯度均值和标准差在各个 epoch 中的变化"

fig, ax = plt.subplots(3, 1, sharex=True, constrained_layout=True, figsize=(8, 12))

ax[0].set_title("梯度均值")

for key in gradhistory[0]:

ax[0].plot(range(len(gradhistory)), [w[key].mean() for w in gradhistory], label=key)

ax[0].legend()

ax[1].set_title("标准差")

for key in gradhistory[0]:

ax[1].semilogy(range(len(gradhistory)), [w[key].std() for w in gradhistory], label=key)

ax[1].legend()

ax[2].set_title("损失")

ax[2].plot(range(len(losshistory)), losshistory)

plt.show()

model = make_mlp("sigmoid", initializer, "sigmoid")

print("训练前：准确率", accuracy_score(y, (model(X) > 0.5)))

gradhistory, losshistory = train_model(X, y, model)

print("训练后：准确率", accuracy_score(y, (model(X) > 0.5)))

plot_gradient(gradhistory, losshistory)

它报告了一个较弱的分类结果

Before training: Accuracy 0.5
After training: Accuracy 0.652

1 2	训练前：准确率 0.5 训练后：准确率 0.652

我们得到的图表显示了梯度消失

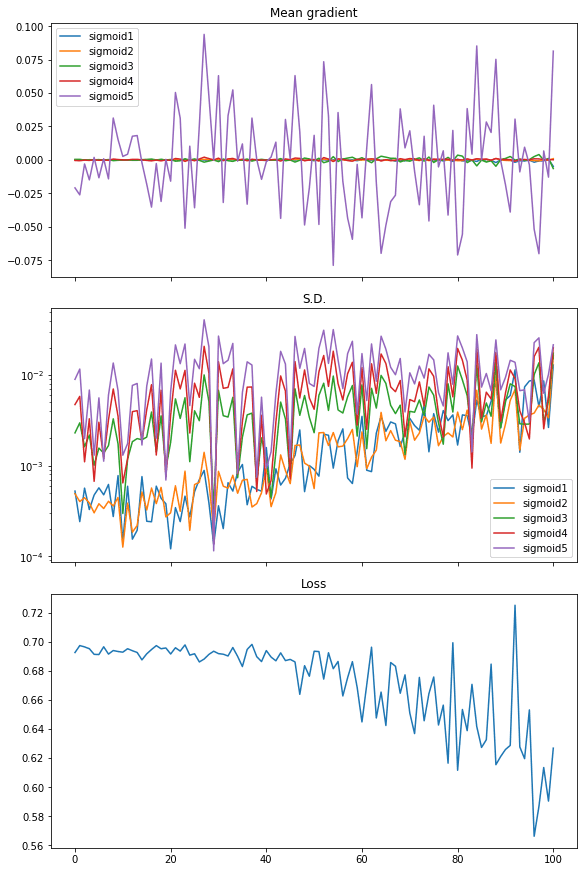
从图中可以看出，损失并没有显著下降。梯度均值（即梯度矩阵中所有元素的均值）只有最后一层有显著值，而所有其他层几乎为零。梯度的标准差大约在 0.01 到 0.001 之间。

使用 tanh 激活函数重复此操作，我们看到了不同的结果，这解释了为什么性能更好

model = make_mlp("tanh", initializer, "tanh")
print("Before training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
gradhistory, losshistory = train_model(X, y, model)
print("After training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
plot_gradient(gradhistory, losshistory)

model = make_mlp("tanh", initializer, "tanh")

print("训练前：准确率", accuracy_score(y, (model(X) > 0.5)))

gradhistory, losshistory = train_model(X, y, model)

print("训练后：准确率", accuracy_score(y, (model(X) > 0.5)))

plot_gradient(gradhistory, losshistory)

Before training: Accuracy 0.502
After training: Accuracy 0.994

1 2	训练前：准确率 0.502 训练后：准确率 0.994

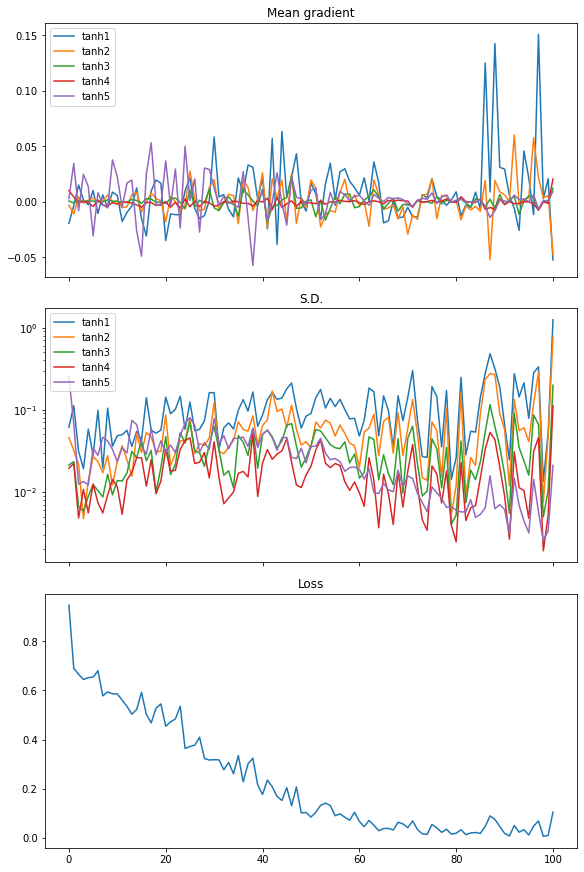
从梯度均值的图中，我们看到每一层的梯度都在均匀地摆动。梯度的标准差也比 Sigmoid 激活函数的情况大一个数量级，大约在 0.1 到 0.01 之间。

最后，我们也可以在修正线性单元 (ReLU) 激活中看到类似的情况。在这种情况下，损失迅速下降，因此我们认为它是神经网络中更有效的激活函数

model = make_mlp("relu", initializer, "relu")
print("Before training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
gradhistory, losshistory = train_model(X, y, model)
print("After training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
plot_gradient(gradhistory, losshistory)

model = make_mlp("relu", initializer, "relu")

print("训练前：准确率", accuracy_score(y, (model(X) > 0.5)))

gradhistory, losshistory = train_model(X, y, model)

print("训练后：准确率", accuracy_score(y, (model(X) > 0.5)))

plot_gradient(gradhistory, losshistory)

Before training: Accuracy 0.503
After training: Accuracy 0.995

1 2	训练前：准确率 0.503 训练后：准确率 0.995

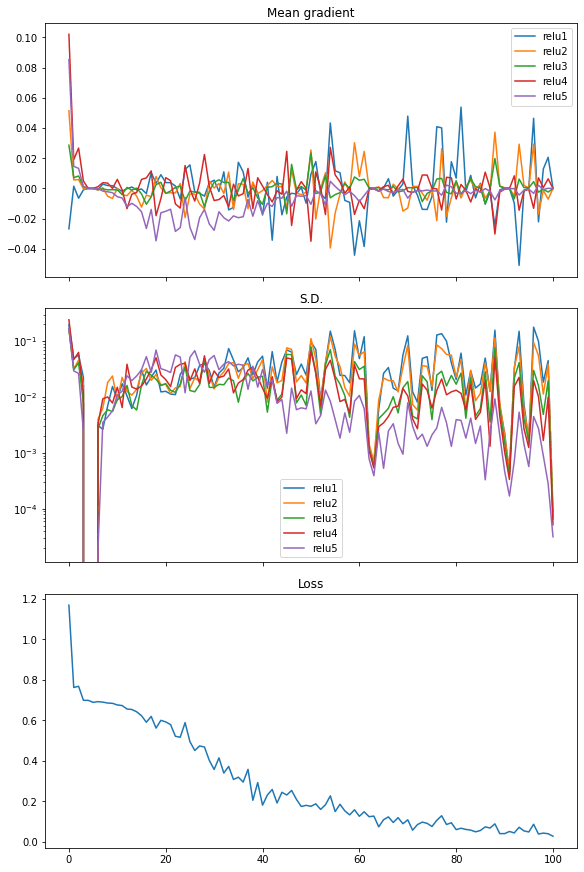
以下是完整的代码

import numpy as np
import tensorflow as tf
from tensorflow.keras.callbacks import Callback
from tensorflow.keras.layers import Dense, Input
from tensorflow.keras import Sequential
from tensorflow.keras.initializers import RandomNormal
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.metrics import accuracy_score

tf.random.set_seed(42)
np.random.seed(42)

# Make data: Two circles on x-y plane as a classification problem
X, y = make_circles(n_samples=1000, factor=0.5, noise=0.1)
plt.figure(figsize=(8,6))
plt.scatter(X[:,0], X[:,1], c=y)
plt.show()

# Test performance with 3-layer binary classification network
model = Sequential([
    Input(shape=(2,)),
    Dense(5, "relu"),
    Dense(1, "sigmoid")
])
model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])
model.fit(X, y, batch_size=32, epochs=100, verbose=0)
print(model.evaluate(X,y))

# Test performance with 3-layer network with sigmoid activation
model = Sequential([
    Input(shape=(2,)),
    Dense(5, "sigmoid"),
    Dense(1, "sigmoid")
])
model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])
model.fit(X, y, batch_size=32, epochs=100, verbose=0)
print(model.evaluate(X,y))

# Test performance with 5-layer network with sigmoid activation
model = Sequential([
    Input(shape=(2,)),
    Dense(5, "sigmoid"),
    Dense(5, "sigmoid"),
    Dense(5, "sigmoid"),
    Dense(1, "sigmoid")
])
model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])
model.fit(X, y, batch_size=32, epochs=100, verbose=0)
print(model.evaluate(X,y))

# Illustrate weights across epochs
class WeightCapture(Callback):
    "Capture the weights of each layer of the model"
    def __init__(self, model):
        super().__init__()
        self.model = model
        self.weights = []
        self.epochs = []

    def on_epoch_end(self, epoch, logs=None):
        self.epochs.append(epoch) # remember the epoch axis
        weight = {}
        for layer in model.layers:
            if not layer.weights:
                continue
            name = layer.weights[0].name.split("/")[0]
            weight[name] = layer.weights[0].numpy()
        self.weights.append(weight)

def make_mlp(activation, initializer, name):
    "Create a model with specified activation and initalizer"
    model = Sequential([
        Input(shape=(2,), name=name+"0"),
        Dense(5, activation=activation, kernel_initializer=initializer, name=name+"1"),
        Dense(5, activation=activation, kernel_initializer=initializer, name=name+"2"),
        Dense(5, activation=activation, kernel_initializer=initializer, name=name+"3"),
        Dense(5, activation=activation, kernel_initializer=initializer, name=name+"4"),
        Dense(1, activation="sigmoid", kernel_initializer=initializer, name=name+"5")
    ])
    return model

def plotweight(capture_cb):
    "Plot the weights' mean and s.d. across epochs"
    fig, ax = plt.subplots(2, 1, sharex=True, constrained_layout=True, figsize=(8, 10))
    ax[0].set_title("Mean weight")
    for key in capture_cb.weights[0]:
        ax[0].plot(capture_cb.epochs, [w[key].mean() for w in capture_cb.weights], label=key)
    ax[0].legend()
    ax[1].set_title("S.D.")
    for key in capture_cb.weights[0]:
        ax[1].plot(capture_cb.epochs, [w[key].std() for w in capture_cb.weights], label=key)
    ax[1].legend()
    plt.show()

initializer = RandomNormal(mean=0, stddev=1)
batch_size = 32
n_epochs = 100

# Sigmoid activation
model = make_mlp("sigmoid", initializer, "sigmoid")
capture_cb = WeightCapture(model)
capture_cb.on_epoch_end(-1)
model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])
print("Before training: Accuracy", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))
model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=0)
print("After training: Accuracy", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))
print(model.evaluate(X,y))
plotweight(capture_cb)

# tanh activation
model = make_mlp("tanh", initializer, "tanh")
capture_cb = WeightCapture(model)
capture_cb.on_epoch_end(-1)
model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])
print("Before training: Accuracy", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))
model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=0)
print("After training: Accuracy", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))
print(model.evaluate(X,y))
plotweight(capture_cb)

# relu activation
model = make_mlp("relu", initializer, "relu")
capture_cb = WeightCapture(model)
capture_cb.on_epoch_end(-1)
model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])
print("Before training: Accuracy", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))
model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=0)
print("After training: Accuracy", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))
print(model.evaluate(X,y))
plotweight(capture_cb)

# Show gradient across epochs
optimizer = tf.keras.optimizers.RMSprop()
loss_fn = tf.keras.losses.BinaryCrossentropy()

def train_model(X, y, model, n_epochs=n_epochs, batch_size=batch_size):
    "Run training loop manually"
    train_dataset = tf.data.Dataset.from_tensor_slices((X, y))
    train_dataset = train_dataset.shuffle(buffer_size=1024).batch(batch_size)

    gradhistory = []
    losshistory = []
    def recordweight():
        data = {}
        for g,w in zip(grads, model.trainable_weights):
            if '/kernel:' not in w.name:
                continue # skip bias
            name = w.name.split("/")[0]
            data[name] = g.numpy()
        gradhistory.append(data)
        losshistory.append(loss_value.numpy())
    for epoch in range(n_epochs):
        for step, (x_batch_train, y_batch_train) in enumerate(train_dataset):
            with tf.GradientTape() as tape:
                y_pred = model(x_batch_train, training=True)
                loss_value = loss_fn(y_batch_train, y_pred)

            grads = tape.gradient(loss_value, model.trainable_weights)
            optimizer.apply_gradients(zip(grads, model.trainable_weights))

            if step == 0:
                recordweight()
    # After all epochs, record again
    recordweight()
    return gradhistory, losshistory

def plot_gradient(gradhistory, losshistory):
    "Plot gradient mean and sd across epochs"
    fig, ax = plt.subplots(3, 1, sharex=True, constrained_layout=True, figsize=(8, 12))
    ax[0].set_title("Mean gradient")
    for key in gradhistory[0]:
        ax[0].plot(range(len(gradhistory)), [w[key].mean() for w in gradhistory], label=key)
    ax[0].legend()
    ax[1].set_title("S.D.")
    for key in gradhistory[0]:
        ax[1].semilogy(range(len(gradhistory)), [w[key].std() for w in gradhistory], label=key)
    ax[1].legend()
    ax[2].set_title("Loss")
    ax[2].plot(range(len(losshistory)), losshistory)
    plt.show()

model = make_mlp("sigmoid", initializer, "sigmoid")
print("Before training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
gradhistory, losshistory = train_model(X, y, model)
print("After training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
plot_gradient(gradhistory, losshistory)

model = make_mlp("tanh", initializer, "tanh")
print("Before training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
gradhistory, losshistory = train_model(X, y, model)
print("After training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
plot_gradient(gradhistory, losshistory)

model = make_mlp("relu", initializer, "relu")
print("Before training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
gradhistory, losshistory = train_model(X, y, model)
print("After training: Accuracy", accuracy_score(y, (model(X) > 0.5)))
plot_gradient(gradhistory, losshistory)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

import numpy as np

import tensorflow as tf

from tensorflow.keras.callbacks import Callback

from tensorflow.keras.layers import Dense, Input

from tensorflow.keras import Sequential

from tensorflow.keras.initializers import RandomNormal

import matplotlib.pyplot as plt

from sklearn.datasets import make_circles

from sklearn.metrics import accuracy_score

tf.random.set_seed(42)

np.random.seed(42)

# 制作数据：xy 平面上的两个圆圈作为分类问题

X, y = make_circles(n_samples=1000, factor=0.5, noise=0.1)

plt.figure(figsize=(8,6))

plt.scatter(X[:,0], X[:,1], c=y)

plt.show()

# 使用 3 层二分类网络测试性能

model = Sequential([

Input(shape=(2,)),

Dense(5, "relu"),

Dense(1, "sigmoid")

])

model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])

model.fit(X, y, batch_size=32, epochs=100, verbose=0)

print(model.evaluate(X,y))

# 使用 3 层 sigmoid 激活网络测试性能

model = Sequential([

Input(shape=(2,)),

Dense(5, "sigmoid"),

Dense(1, "sigmoid")

])

model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])

model.fit(X, y, batch_size=32, epochs=100, verbose=0)

print(model.evaluate(X,y))

# 使用 5 层 sigmoid 激活网络测试性能

model = Sequential([

Input(shape=(2,)),

Dense(5, "sigmoid"),

Dense(1, "sigmoid")

])

model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["acc"])

model.fit(X, y, batch_size=32, epochs=100, verbose=0)

print(model.evaluate(X,y))

# 演示权重在各个 epoch 中的变化

class WeightCapture(Callback):

"捕获模型每一层的权重"

def __init__(self, model):

super().__init__()

self.model = model

self.weights = []

self.epochs = []

def on_epoch_end(self, epoch, logs=None):

self.epochs.append(epoch) # 记住 epoch 轴

weight = {}

for layer in model.layers:

if not layer.weights:

continue

name = layer.weights[0].name.split("/")[0]

weight[name] = layer.weights[0].numpy()

self.weights.append(weight)

def make_mlp(activation, initializer, name):

"使用指定的激活函数和初始化器创建模型"

model = Sequential([

Input(shape=(2,), name=name+"0"),

Dense(5, activation=activation, kernel_initializer=initializer, name=name+"1"),

Dense(5, activation=activation, kernel_initializer=initializer, name=name+"2"),

Dense(5, activation=activation, kernel_initializer=initializer, name=name+"3"),

Dense(5, activation=activation, kernel_initializer=initializer, name=name+"4"),

Dense(1, activation="sigmoid", kernel_initializer=initializer, name=name+"5")

])

返回 model

def plotweight(capture_cb):

"绘制权重在各个 epoch 中的平均值和标准差"

fig, ax = plt.subplots(2, 1, sharex=True, constrained_layout=True, figsize=(8, 10))

ax[0].set_title("权重均值")

for key in capture_cb.weights[0]:

ax[0].plot(capture_cb.epochs, [w[key].mean() for w in capture_cb.weights], label=key)

ax[0].legend()

ax[1].set_title("标准差")

for key in capture_cb.weights[0]:

ax[1].plot(capture_cb.epochs, [w[key].std() for w in capture_cb.weights], label=key)

ax[1].legend()

plt.show()

initializer = RandomNormal(mean=0, stddev=1)

batch_size = 32

n_epochs = 100

# Sigmoid 激活

model = make_mlp("sigmoid", initializer, "sigmoid")

capture_cb = WeightCapture(model)

capture_cb.on_epoch_end(-1)

model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])

print("训练前：准确率", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))

model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=0)

print("训练后：准确率", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))

print(model.evaluate(X,y))

plotweight(capture_cb)

# tanh 激活

model = make_mlp("tanh", initializer, "tanh")

capture_cb = WeightCapture(model)

capture_cb.on_epoch_end(-1)

model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])

print("训练前：准确率", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))

model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=0)

print("训练后：准确率", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))

print(model.evaluate(X,y))

plotweight(capture_cb)

# relu 激活

model = make_mlp("relu", initializer, "relu")

capture_cb = WeightCapture(model)

capture_cb.on_epoch_end(-1)

model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])

print("训练前：准确率", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))

model.fit(X, y, batch_size=batch_size, epochs=n_epochs, callbacks=[capture_cb], verbose=0)

print("训练后：准确率", accuracy_score(y, (model(X).numpy() > 0.5).astype(int)))

print(model.evaluate(X,y))

plotweight(capture_cb)

# 显示梯度在各个 epoch 中的变化

optimizer = tf.keras.optimizers.RMSprop()

loss_fn = tf.keras.losses.BinaryCrossentropy()

def train_model(X, y, model, n_epochs=n_epochs, batch_size=batch_size):

"手动运行训练循环"

train_dataset = tf.data.Dataset.from_tensor_slices((X, y))

train_dataset = train_dataset.shuffle(buffer_size=1024).batch(batch_size)

gradhistory = []

losshistory = []

def recordweight():

data = {}

for g,w in zip(grads, model.trainable_weights):

if '/kernel:' not in w.name:

continue # 跳过偏差

name = w.name.split("/")[0]

data[name] = g.numpy()

gradhistory.append(data)

losshistory.append(loss_value.numpy())

for epoch in range(n_epochs):

for step, (x_batch_train, y_batch_train) in enumerate(train_dataset):

with tf.GradientTape() as tape:

y_pred = model(x_batch_train, training=True)

loss_value = loss_fn(y_batch_train, y_pred)

grads = tape.gradient(loss_value, model.trainable_weights)

optimizer.apply_gradients(zip(grads, model.trainable_weights))

if step == 0:

recordweight()

# 所有 epoch 结束后，再次记录

recordweight()

return gradhistory, losshistory

def plot_gradient(gradhistory, losshistory):

"绘制梯度均值和标准差在各个 epoch 中的变化"

fig, ax = plt.subplots(3, 1, sharex=True, constrained_layout=True, figsize=(8, 12))

ax[0].set_title("梯度均值")

for key in gradhistory[0]:

ax[0].plot(range(len(gradhistory)), [w[key].mean() for w in gradhistory], label=key)

ax[0].legend()

ax[1].set_title("标准差")

for key in gradhistory[0]:

ax[1].semilogy(range(len(gradhistory)), [w[key].std() for w in gradhistory], label=key)

ax[1].legend()

ax[2].set_title("损失")

ax[2].plot(range(len(losshistory)), losshistory)

plt.show()

model = make_mlp("sigmoid", initializer, "sigmoid")

print("训练前：准确率", accuracy_score(y, (model(X) > 0.5)))

gradhistory, losshistory = train_model(X, y, model)

print("训练后：准确率", accuracy_score(y, (model(X) > 0.5)))

plot_gradient(gradhistory, losshistory)

model = make_mlp("tanh", initializer, "tanh")

print("训练前：准确率", accuracy_score(y, (model(X) > 0.5)))

gradhistory, losshistory = train_model(X, y, model)

print("训练后：准确率", accuracy_score(y, (model(X) > 0.5)))

plot_gradient(gradhistory, losshistory)

model = make_mlp("relu", initializer, "relu")

print("训练前：准确率", accuracy_score(y, (model(X) > 0.5)))

gradhistory, losshistory = train_model(X, y, model)

print("训练后：准确率", accuracy_score(y, (model(X) > 0.5)))

plot_gradient(gradhistory, losshistory)

Glorot 初始化

我们没有在上面的代码中演示，但 Glorot 和 Bengio 论文中最著名的成果是 Glorot 初始化。它建议用均匀分布初始化神经网络层的权重

因此，当初始化深度网络时，归一化因子可能很重要，因为层之间存在乘法效应，我们建议采用以下初始化过程，以大致满足我们随着网络向上或向下移动时保持激活方差和反向传播梯度方差一致的目标。我们称之为归一化初始化
$$
W \sim U\Big[-\frac{\sqrt{6}}{\sqrt{n_j+n_{j+1}}}, \frac{\sqrt{6}}{\sqrt{n_j+n_{j+1}}}\Big]
$$

——《理解训练深度前馈神经网络的难度》（2010）

这是从线性激活中推导出来的，条件是梯度的标准差在各层之间保持一致。在 sigmoid 和 tanh 激活中，线性区域很窄。因此我们可以理解为什么 ReLU 是解决梯度消失问题的关键。与替换激活函数相比，改变权重初始化在帮助解决梯度消失问题方面的影响不那么显著。但这可以作为您探索如何帮助改进结果的练习。

总结

在本教程中，您直观地看到了修正线性单元 (ReLU) 如何帮助解决梯度消失问题。

具体来说，你学到了：

梯度消失问题如何影响神经网络的性能
为什么 ReLU 激活是梯度消失问题的解决方案
如何使用自定义回调在 Keras 训练循环中提取数据
如何编写自定义训练循环
如何从神经网络中的层读取权重和梯度

关于此主题的更多信息

使用 CNN 进行金融时间序列预测

拉格朗日乘子法：支持向量机背后的理论（第一部分：可分离情况）

对《可视化梯度消失问题》的 15 条回复

Jeremy 2021 年 11 月 19 日上午 11:32 #

Tam 博士，

这又是一篇出色的文章！我还有几周就完成应用数学硕士学位了，虽然我们在几门课程中以非常详细的数学方式解决了梯度消失问题，但我们从未对这个问题进行图形分析。您在这里的工作真正阐明了这一点，我对此表示感谢！希望有一天能看到您出版一本书，将您所有辛苦获得的知识汇集一处。

回复
- Adrian Tam 2021 年 11 月 20 日凌晨 1:32 #
  
  感谢您的认可。很高兴您喜欢。
  
  回复
The_PP 2021 年 11 月 21 日上午 5:42 #

这是一篇非常棒的文章！我只是想问我应该如何重新开始编写人工智能代码，我已经一年左右没有接触了（由于许多原因），现在我学习机械工程（虽然我们还没有接触到机器学习 - 在 Matlab 中），时间很少。

您有什么快速入门课程吗？我不想再学习 fast.ai 了，那花了我太多时间。

回复
- Adrian Tam 2021 年 11 月 21 日上午 7:57 #
  
  我认为最接近的是这个博客上的迷你课程系列。
  
  回复
- Guillermo Álvarez 2022 年 5 月 13 日上午 6:33 #
  
  我的意思是，例如，您在本教程中显示的带有 Relu 激活的示例中的梯度，除了 Relu5，其他层在第一个 epoch（可能不是第一个）和最后一个 epoch 中似乎具有相似的平均值。
  
  回复
Mohit Prashanth 2022 年 1 月 15 日上午 8:02 #

你好 Adrian，
非常感谢您撰写本文。本文和本网站上的其他文章对我帮助极大。关于本文我有两个问题。
1) 您为什么没有使用梯度绝对值的均值来确定梯度消失？例如，如果一层中有两个神经元，一个变化 -0.25，另一个变化 0.25，那么取它们的均值得到 0，尽管梯度并没有消失。
2) 随着训练的进行，我们是否期望梯度绝对值的均值减小到零或接近零（表示权重不再变化）？

回复
- James Carmichael 2022 年 2 月 21 日下午 2:13 #
  
  嗨 Mohit…也许以下内容能提供清晰的解释。
  
  https://www.analyticsvidhya.com/blog/2021/06/the-challenge-of-vanishing-exploding-gradients-in-deep-neural-networks/
  
  回复
Guillermo Álvarez 2022 年 5 月 11 日上午 7:14 #

很棒的文章！非常感谢。
有一点我很难理解。为什么每个 epoch 的梯度平均值都相似？据我所知，梯度在训练开始时会更大，随着参数的改进，梯度会越来越接近零。这是我一直看到但从未理解的地方。
再次感谢这个网站

回复
- James Carmichael 2022 年 5 月 13 日凌晨 1:04 #
  
  嗨 Guillermo…您的最终梯度值与第一个梯度值相比如何？
  
  回复
  - Guillermo Álvarez 2022 年 5 月 14 日凌晨 3:04 #
    
    我在另一个帖子中回复了，抱歉。我的意思是，例如，您在本教程中显示的带有 Relu 激活的示例中的梯度，除了 Relu5，其他层在第一个 epoch（可能不是第一个）和最后一个 epoch 中似乎具有相似的平均值。
    
    回复
Anuj Lahoty 2023 年 3 月 12 日凌晨 12:05 #

精彩的解释，非常有帮助。

回复
- James Carmichael 2023 年 3 月 12 日上午 10:09 #
  
  谢谢 Anuj！我们非常感谢您的反馈和支持！
  
  回复
Jason 2023 年 3 月 21 日下午 4:02 #

我尝试运行示例代码，出现以下错误。我喜欢这个网站，有很多很棒的解释。我会尝试及时修复错误，但想分享一下，它在 Google Colab 上运行的。

KeyError 回溯（最近的调用在最后）
in
189 model = make_mlp(“tanh”, initializer, “tanh”)
190 print(“训练前：准确度”, accuracy_score(y, (model(X) > 0.5)))
–> 191 gradhistory, losshistory = train_model(X, y, model)
192 print(“训练后：准确度”, accuracy_score(y, (model(X) > 0.5)))
193 plot_gradient(gradhistory, losshistory)

11 帧
在 train_model(X, y, model, n_epochs, batch_size) 中
158
159 grads = tape.gradient(loss_value, model.trainable_weights)
–> 160 optimizer.apply_gradients(zip(grads, model.trainable_weights))
161
162 if step == 0

/usr/local/lib/python3.9/dist-packages/keras/optimizers/optimizer_experimental/optimizer.py 在 apply_gradients(self, grads_and_vars, name, skip_gradients_aggregation, **kwargs) 中
1138 if not skip_gradients_aggregation and experimental_aggregate_gradients
1139 grads_and_vars = self.aggregate_gradients(grads_and_vars)
-> 1140 return super().apply_gradients(grads_and_vars, name=name)
1141
1142 def _apply_weight_decay(self, variables)

/usr/local/lib/python3.9/dist-packages/keras/optimizers/optimizer_experimental/optimizer.py 在 apply_gradients(self, grads_and_vars, name) 中
632 self._apply_weight_decay(trainable_variables)
633 grads_and_vars = list(zip(grads, trainable_variables))
–> 634 iteration = self._internal_apply_gradients(grads_and_vars)
635
636 # 应用梯度后应用变量约束。

/usr/local/lib/python3.9/dist-packages/keras/optimizers/optimizer_experimental/optimizer.py 在 _internal_apply_gradients(self, grads_and_vars) 中
1164
1165 def _internal_apply_gradients(self, grads_and_vars)
-> 1166 return tf.__internal__.distribute.interim.maybe_merge_call(
1167 self._distributed_apply_gradients_fn,
1168 self._distribution_strategy,

/usr/local/lib/python3.9/dist-packages/tensorflow/python/distribute/merge_call_interim.py 在 maybe_merge_call(fn, strategy, *args, **kwargs) 中
49 “””
50 if strategy_supports_no_merge_call()
—> 51 return fn(strategy, *args, **kwargs)
52 else
53 return distribution_strategy_context.get_replica_context().merge_call(

/usr/local/lib/python3.9/dist-packages/keras/optimizers/optimizer_experimental/optimizer.py 在 _distributed_apply_gradients_fn(self, distribution, grads_and_vars, **kwargs) 中
1214
1215 for grad, var in grads_and_vars
-> 1216 distribution.extended.update(
1217 var, apply_grad_to_update_var, args=(grad,), group=False
1218 )

/usr/local/lib/python3.9/dist-packages/tensorflow/python/distribute/distribute_lib.py 在 update(self, var, fn, args, kwargs, group) 中
2635 fn, autograph_ctx.control_status_ctx(), convert_by_default=False)
2636 with self._container_strategy().scope()
-> 2637 return self._update(var, fn, args, kwargs, group)
2638 else
2639 return self._replica_ctx_update(

/usr/local/lib/python3.9/dist-packages/tensorflow/python/distribute/distribute_lib.py 在 _update(self, var, fn, args, kwargs, group) 中
3708 # _update() 和 _update_non_slot() 的实现是相同的
3709 # 除了 _update() 将 `var` 作为第一个参数传递给 `fn()`。
-> 3710 return self._update_non_slot(var, fn, (var,) + tuple(args), kwargs, group)
3711
3712 def _update_non_slot(self, colocate_with, fn, args, kwargs, should_group)

/usr/local/lib/python3.9/dist-packages/tensorflow/python/distribute/distribute_lib.py 在 _update_non_slot(self, colocate_with, fn, args, kwargs, should_group) 中
3714 # 一旦该值被用于其他用途。
3715 with UpdateContext(colocate_with)
-> 3716 result = fn(*args, **kwargs)
3717 if should_group
3718 return result

/usr/local/lib/python3.9/dist-packages/tensorflow/python/autograph/impl/api.py 在 wrapper(*args, **kwargs) 中
593 def wrapper(*args, **kwargs)
594 with ag_ctx.ControlStatusCtx(status=ag_ctx.Status.UNSPECIFIED)
–> 595 return func(*args, **kwargs)
596
597 if inspect.isfunction(func) or inspect.ismethod(func)

/usr/local/lib/python3.9/dist-packages/keras/optimizers/optimizer_experimental/optimizer.py 在 apply_grad_to_update_var(var, grad) 中
1211 return self._update_step_xla(grad, var, id(self._var_key(var)))
1212 else
-> 1213 return self._update_step(grad, var)
1214
1215 for grad, var in grads_and_vars

/usr/local/lib/python3.9/dist-packages/keras/optimizers/optimizer_experimental/optimizer.py 在 _update_step(self, gradient, variable) 中
214 return
215 if self._var_key(variable) not in self._index_dict
–> 216 raise KeyError(
217 f”优化器无法识别变量 {variable.name}。 ”
218 “这通常意味着您正在尝试调用优化器来 ”

KeyError: ‘优化器无法识别变量 tanh1/kernel:0。这通常意味着您正在尝试调用优化器来单独更新模型的不同部分。请在训练循环之前使用完整的可训练变量列表调用 `optimizer.build(variables)` 或使用旧式优化器 `tf.keras.optimizers.legacy.{self.__class__.__name__}`。’

回复
- James Carmichael 2023年3月22日上午10:01 #
  
  你好 Jason…请澄清您是手动输入代码还是复制粘贴的？另外，您可能想在 Google Colab 中尝试一下。
  
  回复
Michael 2023年5月8日上午9:40 #

对梯度消失问题的精彩分析。感谢。🙂

顺便说一句，我也遇到了同样的编码错误，我是粘贴代码的。

回复

导航

梯度消失问题的可视化

教程概述

多层感知器模型的配置

梯度消失问题的示例

查看每一层的权重

查看每一层的梯度

Glorot 初始化

延伸阅读

总结

今天就开发更好的深度学习模型！

更快地训练，减少过拟合，以及集成方法

为你的项目带来更好的深度学习！

关于此主题的更多信息

对《可视化梯度消失问题》的 15 条回复

发表回复点击此处取消回复。

导航

教程概述

多层感知器模型的配置

梯度消失问题的示例

查看每一层的权重

查看每一层的梯度

Glorot 初始化

延伸阅读

总结

今天就开发更好的深度学习模型！

更快地训练，减少过拟合，以及集成方法

为你的项目带来更好的深度学习！

关于此主题的更多信息

对《可视化梯度消失问题》的 15 条回复

发表回复 点击此处取消回复。

发表回复点击此处取消回复。