权重初始化是开发深度学习神经网络模型时一个重要的设计选择。
历史上,权重初始化涉及使用小的随机数,但在过去十年中,已经开发出更具体的启发式方法,它们利用诸如所使用的激活函数类型和节点输入数量等信息。
这些更定制化的启发式方法可以使得使用随机梯度下降优化算法训练神经网络模型更有效。
在本教程中,您将学习如何为深度学习神经网络实现权重初始化技术。
完成本教程后,您将了解:
- 权重初始化用于在模型在数据集上训练之前,定义神经网络模型中参数的初始值。
- 如何实现Xavier和归一化Xavier权重初始化启发式,用于使用Sigmoid或Tanh激活函数的节点。
- 如何实现He权重初始化启发式,用于使用ReLU激活函数的节点。
让我们开始吧。
- 2020年2月更新:修正了归一化Xavier方程中的一个打字错误。

深度学习神经网络的权重初始化
图片来源:Andres Alvarado,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 神经网络的权重初始化
- Sigmoid和Tanh的权重初始化
- Xavier权重初始化
- 归一化Xavier权重初始化
- ReLU的权重初始化
- He权重初始化
神经网络的权重初始化
权重初始化是神经网络模型设计中的一个重要考虑因素。
神经网络中的节点由称为权重的参数组成,用于计算输入的加权和。
神经网络模型使用一种称为随机梯度下降的优化算法进行拟合,该算法逐步改变网络权重以最小化损失函数,希望最终得到一组能够做出有用预测的模型权重。
这种优化算法需要一个可能的权重值空间中的起始点来开始优化过程。权重初始化是一个将神经网络权重设置为小随机值的过程,这些值定义了神经网络模型优化(学习或训练)的起始点。
……训练深度模型是一项足够困难的任务,以至于大多数算法都受到初始化选择的强烈影响。起始点可以决定算法是否能够收敛,有些起始点非常不稳定,以至于算法遇到数值困难并完全失败。
——《深度学习》,2016年,第301页。
每次神经网络使用不同的权重集进行初始化,都会导致优化过程的起始点不同,并可能导致最终的权重集具有不同的性能特征。
有关每次在相同数据集上训练相同算法时产生不同结果的更多信息,请参阅本教程。
我们不能将所有权重都初始化为0.0,因为优化算法需要误差梯度中的某种不对称性才能有效地开始搜索。
有关为什么我们用随机权重初始化神经网络的更多信息,请参阅本教程。
历史上,权重初始化遵循简单的启发式方法,例如
- 范围在 [-0.3, 0.3] 内的小随机值
- 范围在 [0, 1] 内的小随机值
- 范围在 [-1, 1] 内的小随机值
这些启发式方法通常仍然有效。
我们几乎总是将模型中的所有权重初始化为从高斯分布或均匀分布中随机抽取的值。选择高斯分布还是均匀分布似乎并不重要,但尚未进行详尽研究。然而,初始分布的尺度对优化过程的结果和网络的泛化能力都有很大影响。
——《深度学习》,2016年,第302页。
然而,在过去十年中,已经开发出更定制化的方法,这些方法已成为事实上的标准,因为它们可能导致更有效的优化(模型训练)过程。
这些现代权重初始化技术根据被初始化节点中使用的激活函数类型进行划分,例如“Sigmoid和Tanh”以及“ReLU”。
接下来,让我们仔细看看这些用于带有Sigmoid和Tanh激活函数的节点的现代权重初始化启发式方法。
Sigmoid和Tanh的权重初始化
当前用于初始化使用Sigmoid或TanH激活函数的神经网络层和节点权重的标准方法称为“Glorot”或“Xavier”初始化。
它以目前在Google DeepMind担任研究科学家的Xavier Glorot的名字命名,并在Xavier和Yoshua Bengio于2010年发表的题为“理解深度前馈神经网络训练的困难”的论文中进行了描述。
这种权重初始化方法有两个版本,我们称之为“Xavier”和“归一化Xavier”。
Glorot和Bengio提出采用一个适当缩放的均匀分布进行初始化。这被称为“Xavier”初始化 […] 它的推导基于激活是线性的假设。这个假设对于ReLU和PReLU是无效的。
——《深入研究整流器:超越ImageNet分类的人类水平性能》,2015年。
这两种方法都是在假设激活函数是线性的情况下推导出来的,然而,它们已成为Sigmoid和Tanh等非线性激活函数的标准,但不适用于ReLU。
让我们依次仔细看看每一个。
Xavier权重初始化
Xavier初始化方法计算为在范围 -(1/sqrt(n)) 和 1/sqrt(n) 之间均匀概率分布(U)的随机数,其中 n 是节点的输入数量。
- 权重 = U [-(1/sqrt(n)), 1/sqrt(n)]
我们可以在Python中直接实现它。
下面的示例假设一个节点有10个输入,然后计算范围的下限和上限,并计算1000个初始权重值,这些值可用于使用sigmoid或tanh激活函数的层或网络中的节点。
计算权重后,打印下限和上限,以及生成的权重的最小值、最大值、平均值和标准差。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# Xavier权重初始化示例 from math import sqrt from numpy import mean from numpy.random import rand # 前一层中的节点数 n = 10 # 计算权重的范围 lower, upper = -(1.0 / sqrt(n)), (1.0 / sqrt(n)) # 生成随机数 numbers = rand(1000) # 缩放到所需范围 scaled = lower + numbers * (upper - lower) # 总结 print(lower, upper) print(scaled.min(), scaled.max()) print(scaled.mean(), scaled.std()) |
运行该示例会生成权重并打印摘要统计信息。
我们可以看到权重值的范围大约在-0.316和0.316之间。这些范围会随着输入减少而变宽,随着输入增加而变窄。
我们可以看到生成的权重符合这些范围,并且平均权重值接近零,标准差接近0.17。
|
1 2 3 |
-0.31622776601683794 0.31622776601683794 -0.3157663248679193 0.3160839282916222 0.006806069733149146 0.17777128902976705 |
查看权重分布如何随输入数量变化也有帮助。
为此,我们可以计算输入数量从1到100的不同情况下的权重初始化边界,并绘制结果。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 |
# 不同输入数量下Xavier权重初始化边界的图 from math import sqrt from matplotlib import pyplot # 定义输入数量从1到100 values = [i for i in range(1, 101)] # 计算每个输入数量的范围 results = [1.0 / sqrt(n) for n in values] # 为每个输入数量创建以0为中心误差条形图 pyplot.errorbar(values, [0.0 for _ in values], yerr=results) pyplot.show() |
运行该示例会创建一个图表,使我们能够比较不同输入值数量的权重范围。
我们可以看到,当输入非常少时,范围很大,例如在-1和1之间或-0.7到-7之间。然后我们可以看到,在20个权重左右,我们的范围迅速缩小到接近-0.1和0.1,并在那里保持相对稳定。
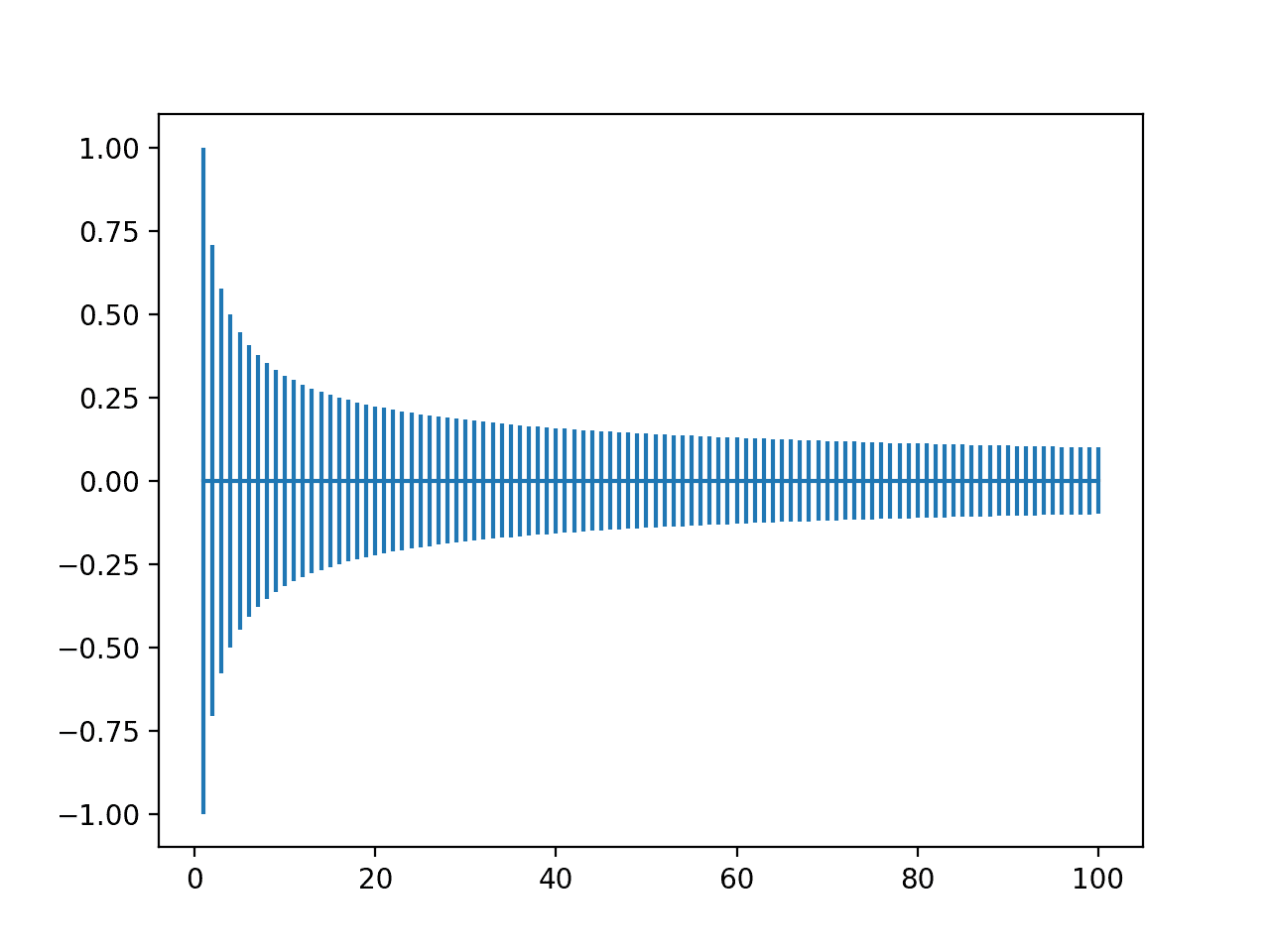
Xavier权重初始化范围随输入数量从1到100变化的图
归一化Xavier权重初始化
归一化Xavier初始化方法计算为在范围 -(sqrt(6)/sqrt(n + m)) 和 sqrt(6)/sqrt(n + m) 之间均匀概率分布(U)的随机数,其中 n 是节点的输入数量(例如前一层的节点数量),而 m 是该层的输出数量(例如当前层的节点数量)。
- 权重 = U [-(sqrt(6)/sqrt(n + m)), sqrt(6)/sqrt(n + m)]
我们可以像上一节一样在Python中直接实现它,并总结1000个生成权重的统计摘要。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 归一化Xavier权重初始化示例 from math import sqrt from numpy import mean from numpy.random import rand # 前一层中的节点数 n = 10 # 下一层的节点数 m = 20 # 计算权重的范围 lower, upper = -(sqrt(6.0) / sqrt(n + m)), (sqrt(6.0) / sqrt(n + m)) # 生成随机数 numbers = rand(1000) # 缩放到所需范围 scaled = lower + numbers * (upper - lower) # 总结 print(lower, upper) print(scaled.min(), scaled.max()) print(scaled.mean(), scaled.std()) |
运行该示例会生成权重并打印摘要统计信息。
我们可以看到权重值的范围大约在-0.447和0.447之间。这些范围会随着输入减少而变宽,随着输入增加而变窄。
我们可以看到生成的权重符合这些范围,并且平均权重值接近零,标准差接近0.17。
|
1 2 3 |
-0.44721359549995787 0.44721359549995787 -0.4447861894315135 0.4463641245392874 -0.01135636099916006 0.2581340352889168 |
查看权重分布如何随输入数量变化也有帮助。
为此,我们可以计算输入数量从1到100以及固定输出数量为10的权重初始化边界,并绘制结果。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 不同输入数量下归一化Xavier权重初始化边界的图 from math import sqrt from matplotlib import pyplot # 定义输入数量从1到100 values = [i for i in range(1, 101)] # 定义输出数量 m = 10 # 计算每个输入数量的范围 results = [1.0 / sqrt(n + m) for n in values] # 为每个输入数量创建以0为中心误差条形图 pyplot.errorbar(values, [0.0 for _ in values], yerr=results) pyplot.show() |
运行该示例会创建一个图表,使我们能够比较不同输入值数量的权重范围。
我们可以看到,当输入较少时,范围开始较宽,大约在-0.3到0.3之间,随着输入数量的增加,范围缩小到大约-0.1到0.1。
与上一节中的非归一化版本相比,初始范围较小,但以相似的速度过渡到紧凑范围。
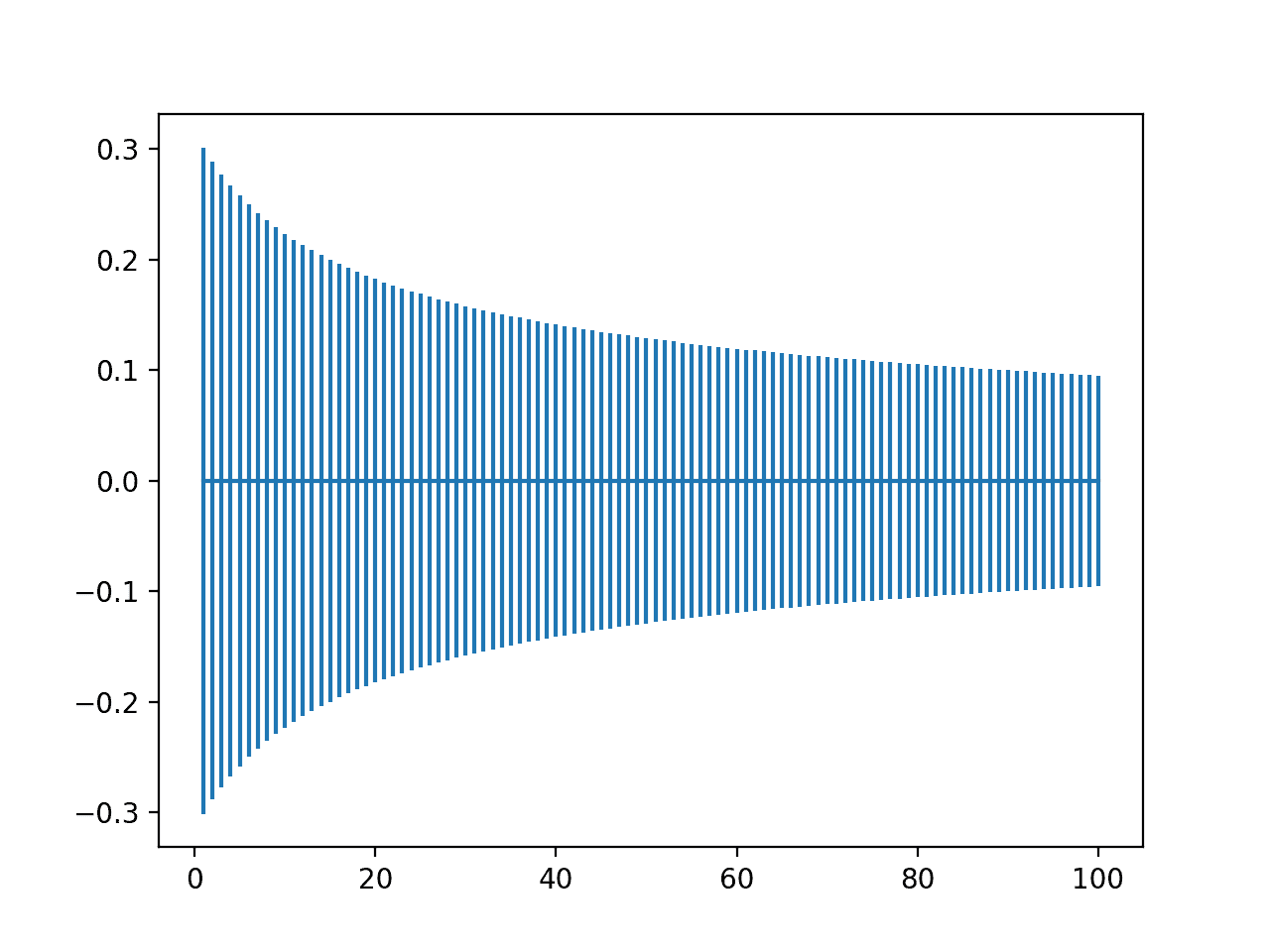
归一化Xavier权重初始化范围随输入数量从1到100变化的图
ReLU的权重初始化
当用于初始化使用修正线性(ReLU)激活函数的网络时,“Xavier”权重初始化被发现存在问题。
因此,开发了一种该方法的修改版本,专门用于使用ReLU激活的节点和层,这在大多数多层感知器和卷积神经网络模型的隐藏层中很流行。
当前用于初始化使用修正线性(ReLU)激活函数的神经网络层和节点权重的标准方法称为“He”初始化。
它以目前在Facebook担任研究科学家的Kaiming He的名字命名,并在Kaiming He等人于2015年发表的题为“深入研究整流器:超越ImageNet分类的人类水平性能”的论文中进行了描述。
He权重初始化
He初始化方法计算为平均值为0.0,标准差为sqrt(2/n)的高斯概率分布(G)的随机数,其中 n 是节点的输入数量。
- 权重 = G (0.0, sqrt(2/n))
我们可以在Python中直接实现它。
下面的示例假设一个节点有10个输入,然后计算高斯分布的标准差,并计算1000个初始权重值,这些值可用于使用ReLU激活函数的层或网络中的节点。
计算权重后,打印计算出的标准差,以及生成的权重的最小值、最大值、平均值和标准差。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# He权重初始化示例 from math import sqrt from numpy.random import randn # 前一层中的节点数 n = 10 # 计算权重的范围 std = sqrt(2.0 / n) # 生成随机数 numbers = randn(1000) # 缩放到所需范围 scaled = numbers * std # 总结 print(std) print(scaled.min(), scaled.max()) print(scaled.mean(), scaled.std()) |
运行该示例会生成权重并打印摘要统计信息。
我们可以看到,计算出的权重标准差的上限大约为0.447。这个标准差会随着输入减少而变大,随着输入增加而变小。
我们可以看到权重的范围大约在-1.573到1.433之间,这接近理论范围约-1.788和1.788,即标准差的四倍,捕捉了高斯分布中99.7%的观测值。我们还可以看到生成的权重的平均值和标准差分别接近规定的0.0和0.447。
|
1 2 3 |
0.4472135954999579 -1.5736761136523203 1.433348584081719 -0.00023406487278826836 0.4522609460629265 |
查看权重分布如何随输入数量变化也有帮助。
为此,我们可以计算输入数量从1到100的不同情况下的权重初始化边界,并绘制结果。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 |
# 不同输入数量下He权重初始化边界的图 from math import sqrt from matplotlib import pyplot # 定义输入数量从1到100 values = [i for i in range(1, 101)] # 计算每个输入数量的范围 results = [sqrt(2.0) / n) for n in values] # 为每个输入数量创建以0为中心误差条形图 pyplot.errorbar(values, [0.0 for _ in values], yerr=results) pyplot.show() |
运行该示例会创建一个图表,使我们能够比较不同输入值数量的权重范围。
我们可以看到,当输入非常少时,范围很大,接近-1.5和1.5或-1.0到-1.0。然后我们可以看到,在20个权重左右,我们的范围迅速下降到接近-0.1和0.1,并在那里保持相对稳定。
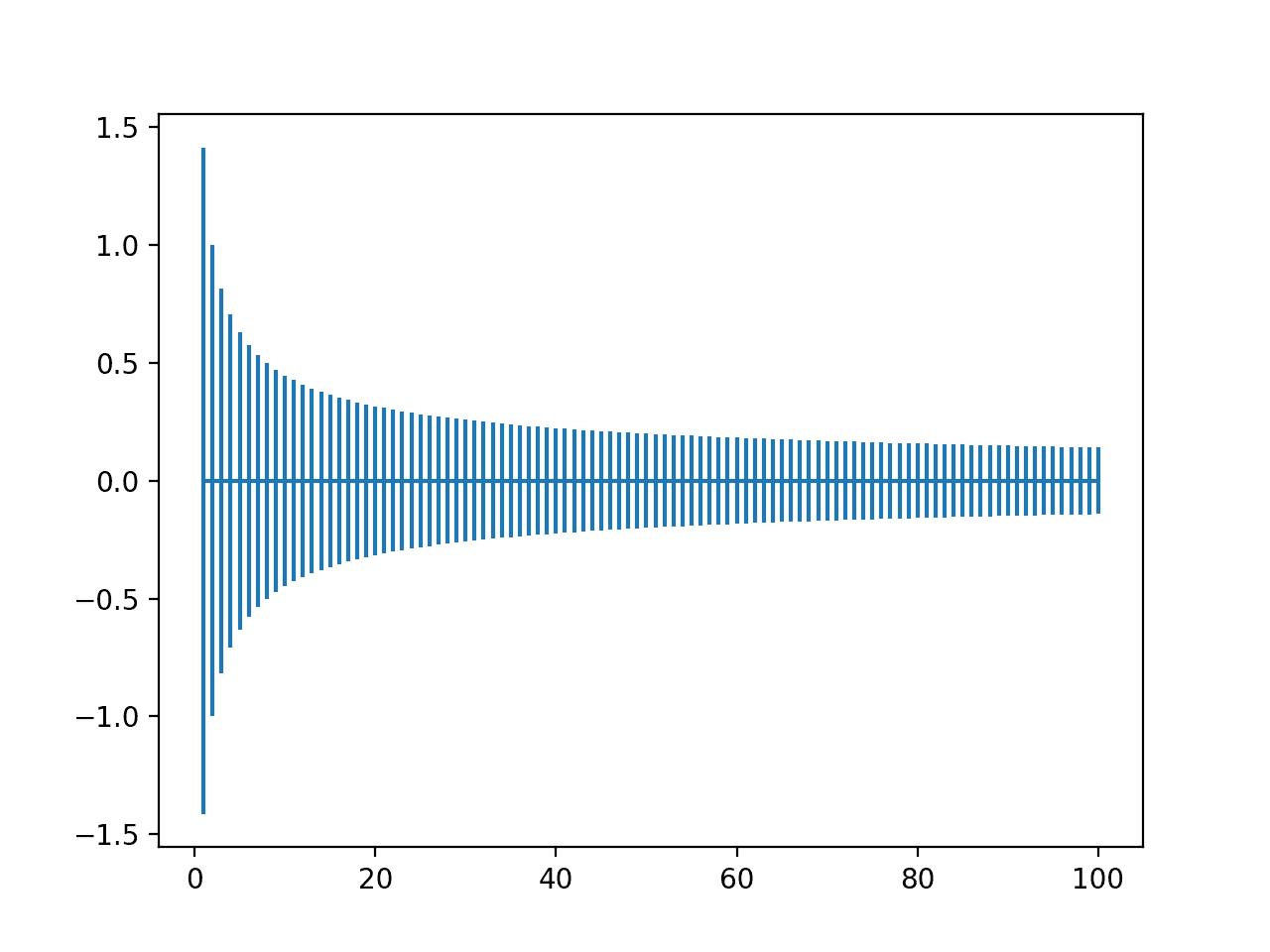
He权重初始化范围随输入数量从1到100变化的图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
论文
- 理解深度前馈神经网络训练的困难, 2010.
- 深入研究整流器:超越ImageNet分类的人类水平性能, 2015.
书籍
- 深度学习, 2016.
总结
在本教程中,您学习了如何为深度学习神经网络实现权重初始化技术。
具体来说,你学到了:
- 权重初始化用于在模型在数据集上训练之前,定义神经网络模型中参数的初始值。
- 如何实现Xavier和归一化Xavier权重初始化启发式,用于使用Sigmoid或Tanh激活函数的节点。
- 如何实现He权重初始化启发式,用于使用ReLU激活函数的节点。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。




DNN中的“节点”是什么?它是层中的通道数还是特征数?
DNN可以是任何模型,但我们假设您指的是多层感知器(MLP)。
MLP中的一个节点接受一个或多个输入,具有一个激活函数,并产生一个输出,该输出可能会传递到下一层的一个或多个节点。
您的解释使我有了更好的理解
谢谢!
精彩的文章!感谢分享。顺便说一句,我在以下部分发现了一些小错误
归一化Xavier权重初始化
归一化Xavier初始化方法计算为在范围 -(sqrt(6)/sqrt(n + n)) 和 sqrt(6)/sqrt(n + n) 之间均匀概率分布(U)的随机数,其中 n 是节点的输入数量(例如前一层的节点数量),m 是该层的输出数量(例如当前层的节点数量)。
* 权重 = U [-(sqrt(6)/sqrt(n + n)), sqrt(6)/sqrt(n + n)]
根据我的理解,第二个
n(sqrt(n + n) -> sqrt(n + m)) 应该是m。供您参考不客气。
谢谢,看起来是打字错误。已修正!
先生,我们如何通过数据增强进一步提高迁移学习Alexnet的决策能力
这里有许多关于更普遍地提高深度学习模型性能的建议
https://machinelearning.org.cn/start-here/#better
谢谢您的解释!
我有一些问题
当softmax作为激活函数时,有没有一种好的权重初始化方法?我一直在努力训练一个以softmax作为输出激活层,输入数据范围在0到1的MLP,似乎我在权重初始化方面有问题。
不客气。
是的,与tanh和sigmoid相同的方法。
高斯概率分布和均匀概率分布有什么区别?
顺便说一句,我喜欢您的网站,它包含了我们成为机器学习专家开发人员所需的一切。我有一半的时间都在您的网站上,它真的帮助我增长了知识,再次感谢您提供了非常有用的数学知识。
区别在于形状。或许可以从这里开始
https://machinelearning.org.cn/continuous-probability-distributions-for-machine-learning/
谢谢
不客气。
您好,我有一个问题。我使用了一个神经网络,并通过遗传算法对其进行了改进。我使用了一个名为Pygad的库。权重范围在9到-9之间,这非常大。当我将范围确定在1到-1之间时,它找到了相同的9到-9之间的范围。解决方案是什么?
你好,Mohammed……我目前无法谈论这个特定的库。但是我确实找到了一些它的入门资料。
https://pygad.readthedocs.io/en/latest/
检测到错误:“-0.7到-7”。
我也认为“he”应该大写。
谢谢您的反馈,Marsel!
为什么权重初始化会涉及小随机数?我理解为什么它们必须是随机的,但为什么它们必须是小的?
嗨,Vicente……较小的数字通常被认为是避免“梯度爆炸”的更好选择
https://machinelearning.org.cn/exploding-gradients-in-neural-networks/
我想知道是否有一种通用的初始化器。一种对relu和tanh都适用且效果很好的?
您好Jason,非常感谢您的博客和解释。我发现它非常非常有用!!
我有一个关于归一化Xavier权重初始化的问题。我不确定我是否理解有误,或者是一个打字错误。
在完整示例中,第8-9行是
是
# 计算每个输入数量的范围
results = [1.0 / sqrt(n + m) for n in values]
应该是?
# 计算每个输入数量的范围
results = [6.0 / sqrt(n + m) for n in values]
感谢您的时间,
Luis
嗨,Luis……以下资源应该能阐明这一点
https://towardsdatascience.com/weight-initialization-in-neural-networks-a-journey-from-the-basics-to-kaiming-954fb9b47c79
谢谢您的讲解
你好塞缪尔……不客气!
如何在神经网络训练循环中实现初始权重?
感谢您的见解
嗨,Joseph……以下资源可能会对您有所帮助
https://www.deeplearning.ai/ai-notes/initialization/index.html