概率不仅仅能用于计算某个事件的可能性,它还可以总结所有可能结果的可能性。
概率论中一个有趣的东西叫做随机变量,而随机变量的每个可能结果与其概率之间的关系被称为概率分布。
概率分布是概率论中一个重要的基础概念,常见的概率分布的名称和形状会让人感到熟悉。概率分布的结构和类型根据随机变量的性质(例如连续或离散)而变化,这反过来又影响了如何总结分布,或者如何计算最可能的结果及其概率。
在这篇文章中,您将发现一个关于概率分布的简明介绍。
阅读本文后,你将了解:
- 概率论中的随机变量具有确定的定义域,可以是连续的,也可以是离散的。
- 概率分布总结了随机变量的可能值与其概率之间的关系。
- 概率密度函数或概率质量函数将值映射到概率,而累积分布函数将小于或等于某个值的结果映射到概率。
通过我的新书《面向机器学习的概率论》,**快速启动您的项目**,书中包含了所有示例的*分步教程*和*Python 源代码*文件。
让我们开始吧。

概率分布简明介绍
照片由 Tom Long 拍摄,保留部分权利。
概述
本教程分为四个部分;它们是
- 随机变量
- 概率分布
- 离散概率分布
- 连续概率分布
随机变量
随机变量是由随机过程产生的量。
在概率论中,随机变量可以取多个可能值中的一个,例如状态空间中的事件。可以为随机变量的特定值或一组值分配一个概率。
在概率建模中,示例数据或实例通常被认为是潜在随机变量的事件、观测值或实现。
— 第336页,《数据挖掘:实用机器学习工具与技术》,第四版,2016年。
随机变量通常用大写字母表示,例如*X*,而随机变量的值则用小写字母和索引表示,例如*x1*、*x2*、*x3*。
像X这样的大写字母表示一个随机变量,而像x这样的小写字母表示该随机变量所取的值。
— 第viii页,《概率论:写给热情的初学者》,2016年。
随机变量可以取的值的集合称为其定义域,随机变量的定义域可以是离散的或连续的。
概率论中的变量称为随机变量,其名称以大写字母开头。[...] 每个随机变量都有一个定义域——它可以取的值的集合。
— 第486页,《人工智能:一种现代方法》,第三版,2009年。
离散随机变量有一组有限的状态:例如,汽车的颜色。值为真或假的随机变量是离散的,被称为布尔随机变量:例如,抛硬币。连续随机变量有一系列数值:例如,人的身高。
- 离散随机变量。值从一组有限的状态中抽取。
- 布尔随机变量。值从集合{真, 假}中抽取。
- 连续随机变量。值从一系列实数值中抽取。
随机变量的值可以通过等号运算符来指定:例如,*X=真*。
随机变量的概率用大写字母*P*或*Pr*作为函数表示;例如,*P(X)*是随机变量*X*所有值的概率。
随机变量某个值的概率可以表示为*P(X=真)*,在这种情况下,它表示随机变量*X*取值为*真*的概率。
想学习机器学习概率吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
概率分布
概率分布是随机变量值的概率摘要。
作为一个分布,当随机变量的所有值排列起来时,随机变量的值与概率的映射会呈现出一种形状。该分布还具有可以度量的通用属性。概率分布的两个重要属性是期望值和方差。在数学上,这些被称为分布的第一矩和第二矩。其他矩包括偏度(第三矩)和峰度(第四矩)。
您可能对统计学中的均值和方差很熟悉,在统计学中,这些概念被推广到除概率分布之外的其他随机变量分布。
期望值是随机变量X的平均值或均值。这是最可能的值或概率最高的结果。它通常表示为大写字母E带方括号的函数:例如,*E[X]*表示*X*的期望值,或*E[f(x)]*,其中函数*f()*用于从*X*的定义域中采样一个值。
随机变量X的期望值(或均值)用E(X)表示…
— 第134页,《概率论:写给热情的初学者》,2016年。
方差是随机变量的值围绕均值的离散程度。这通常表示为函数*Var*;例如,*Var(X)*是随机变量*X*的方差,或*Var(f(x))*是使用函数*f()*从*X*的定义域中抽取的值的方差。
方差的平方根将该值归一化,并被称为标准差。两个变量之间的方差称为协方差,它总结了两个随机变量如何一起变化的线性关系。
- 期望值。随机变量的平均值。
- 方差。值围绕期望值的平均离散程度。
每个随机变量都有其自己的概率分布,尽管许多不同随机变量的概率分布可能具有相同的形状。
大多数常见的概率分布可以用几个参数来定义,并提供了计算期望值和方差的程序。
概率分布的结构会因随机变量是离散的还是连续的而有所不同。
离散概率分布
离散概率分布总结了离散随机变量的概率。
概率质量函数(PMF)定义了离散随机变量的概率分布。它是一个为特定离散值分配概率的函数。
离散概率分布有一个累积分布函数(CDF)。这是一个函数,它为一个离散随机变量的值小于或等于某个特定离散值的概率进行分配。
- 概率质量函数。离散随机变量某个值的概率。
- 累积分布函数。随机变量的值小于或等于某个值的概率。
随机变量的值可能是有序的,也可能不是,这意味着它们可能无法在数轴上排序,例如计数可以,汽车颜色不可以。在这种情况下,PMF和CDF的结构可能是不连续的,或者可能不会在不同值之间形成整洁或平滑的相对概率过渡。
离散随机变量的期望值可以使用众数从样本中计算得出,例如找到最常见的值。PMF中的概率总和等于一。
一些著名的离散概率分布的例子包括:
- 泊松分布。
- 伯努利分布和二项分布。
- 多项分布和多项式分布。
- 离散均匀分布。
一些具有著名离散概率分布的常见领域的例子包括:
- 掷骰子的概率构成离散均匀分布。
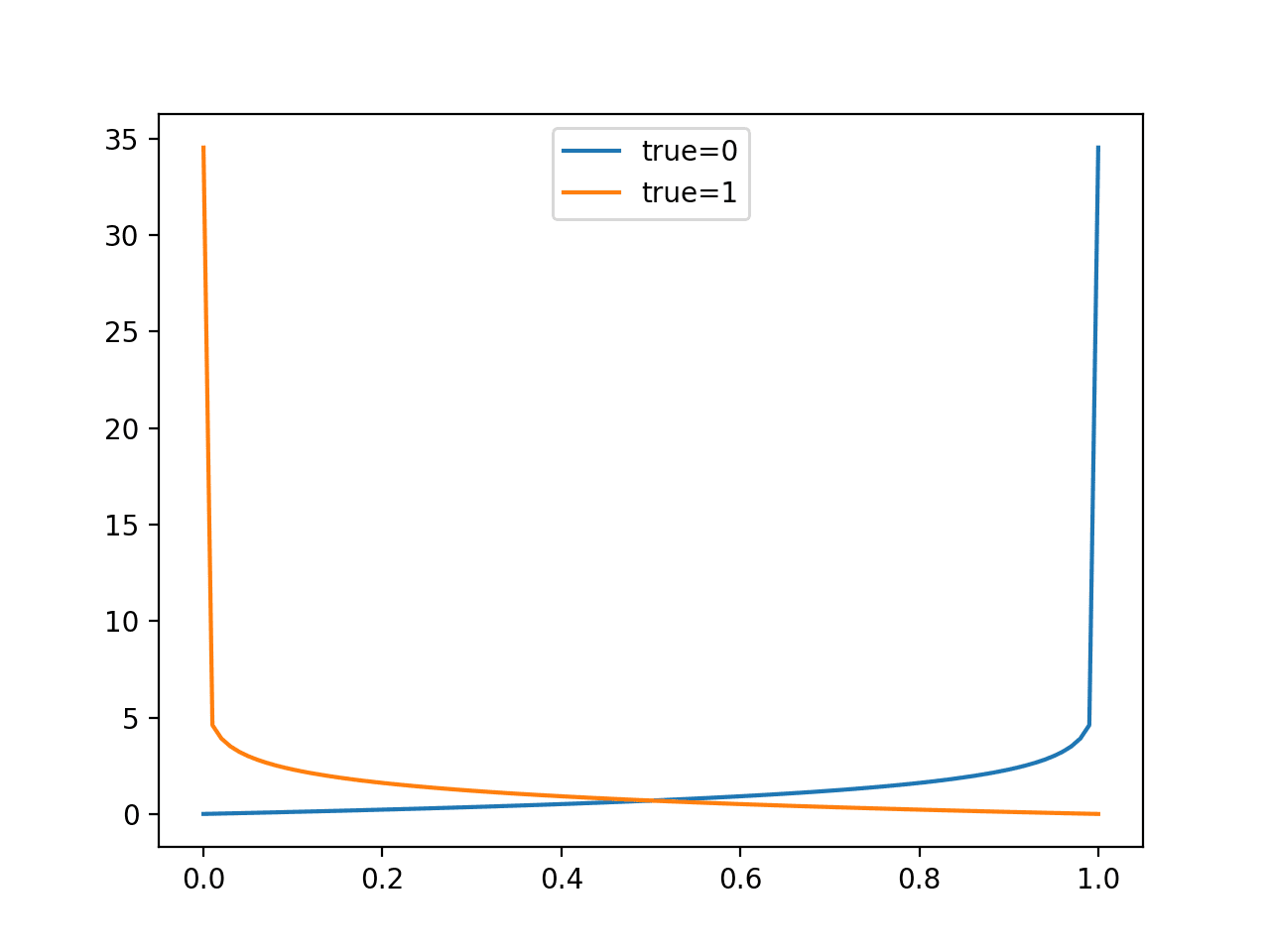
- 抛硬币的概率构成伯努利分布。
- 汽车颜色的概率构成多项分布。
连续概率分布
连续概率分布总结了连续随机变量的概率。
概率密度函数(PDF)定义了连续随机变量的概率分布。注意其名称与离散随机变量的概率质量函数(PMF)有所不同。
与离散概率分布一样,连续概率分布也有一个累积分布函数(CDF),它定义了值小于或等于定义域中某个特定数值的概率。
- 概率分布函数。连续随机变量某个值的概率。
- 累积分布函数。随机变量的值小于或等于某个值的概率。
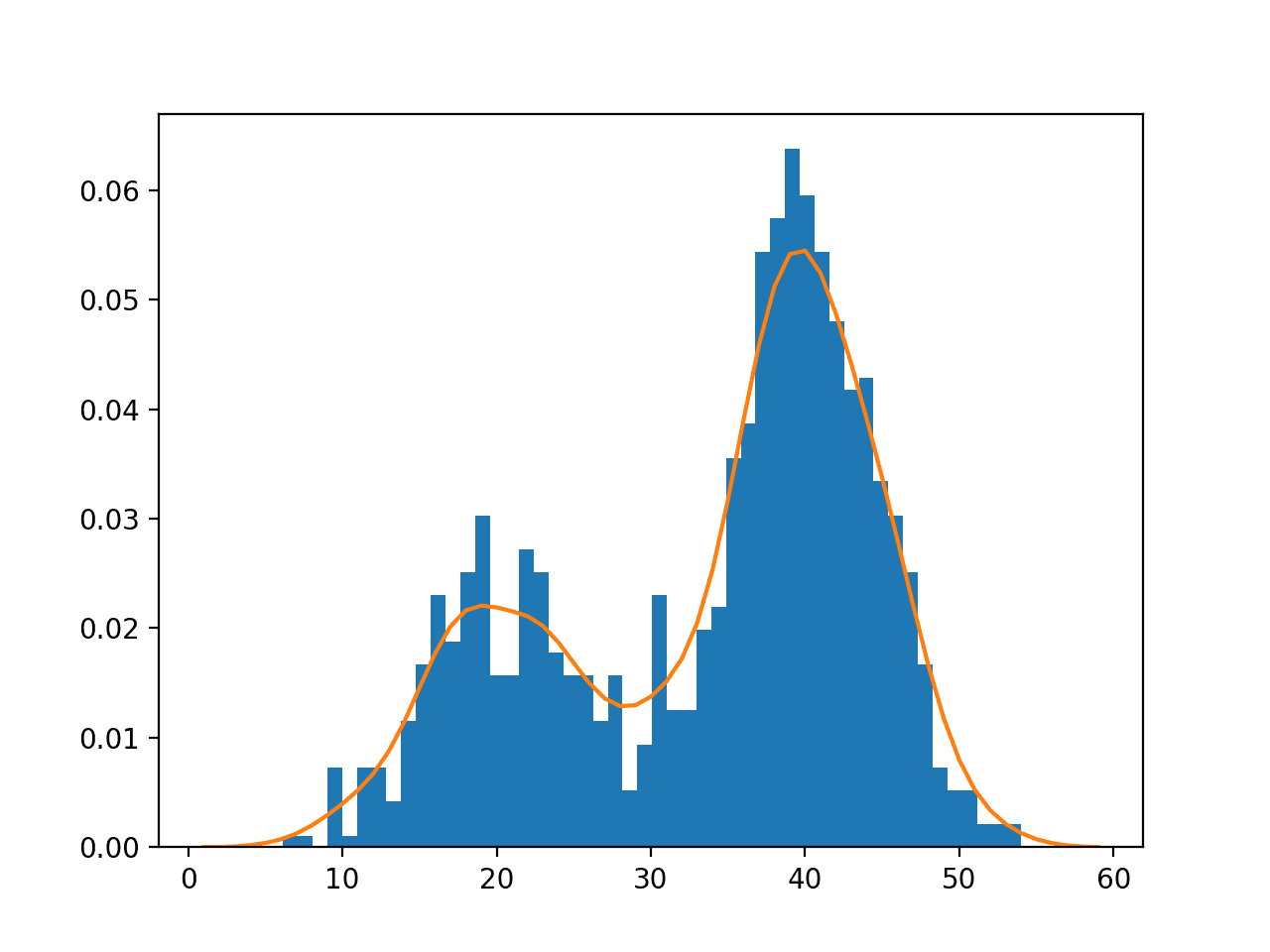
作为一个连续函数,其结构形成一条平滑的曲线。
一些著名的连续概率分布的例子包括:
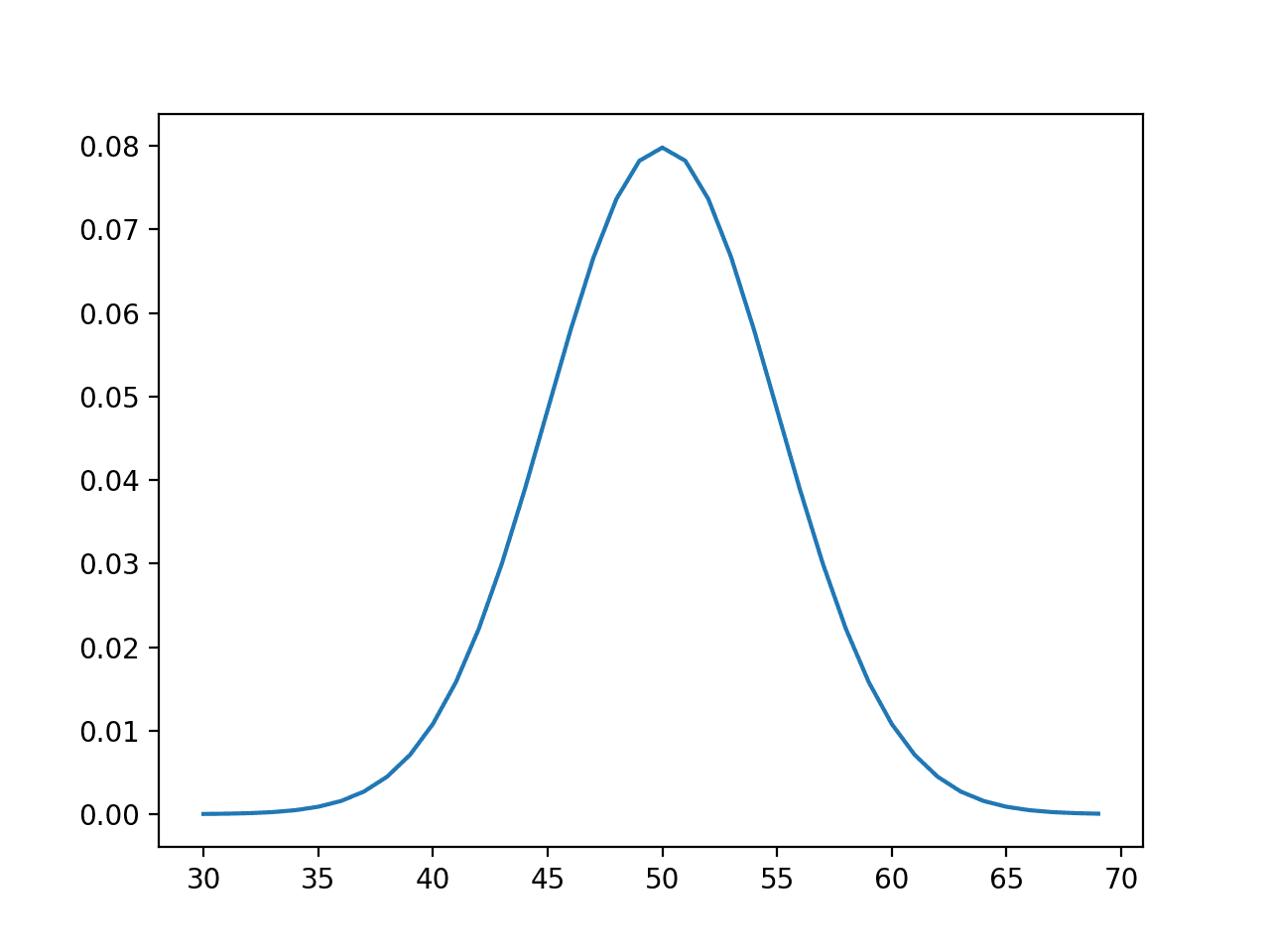
- 正态分布或高斯分布。
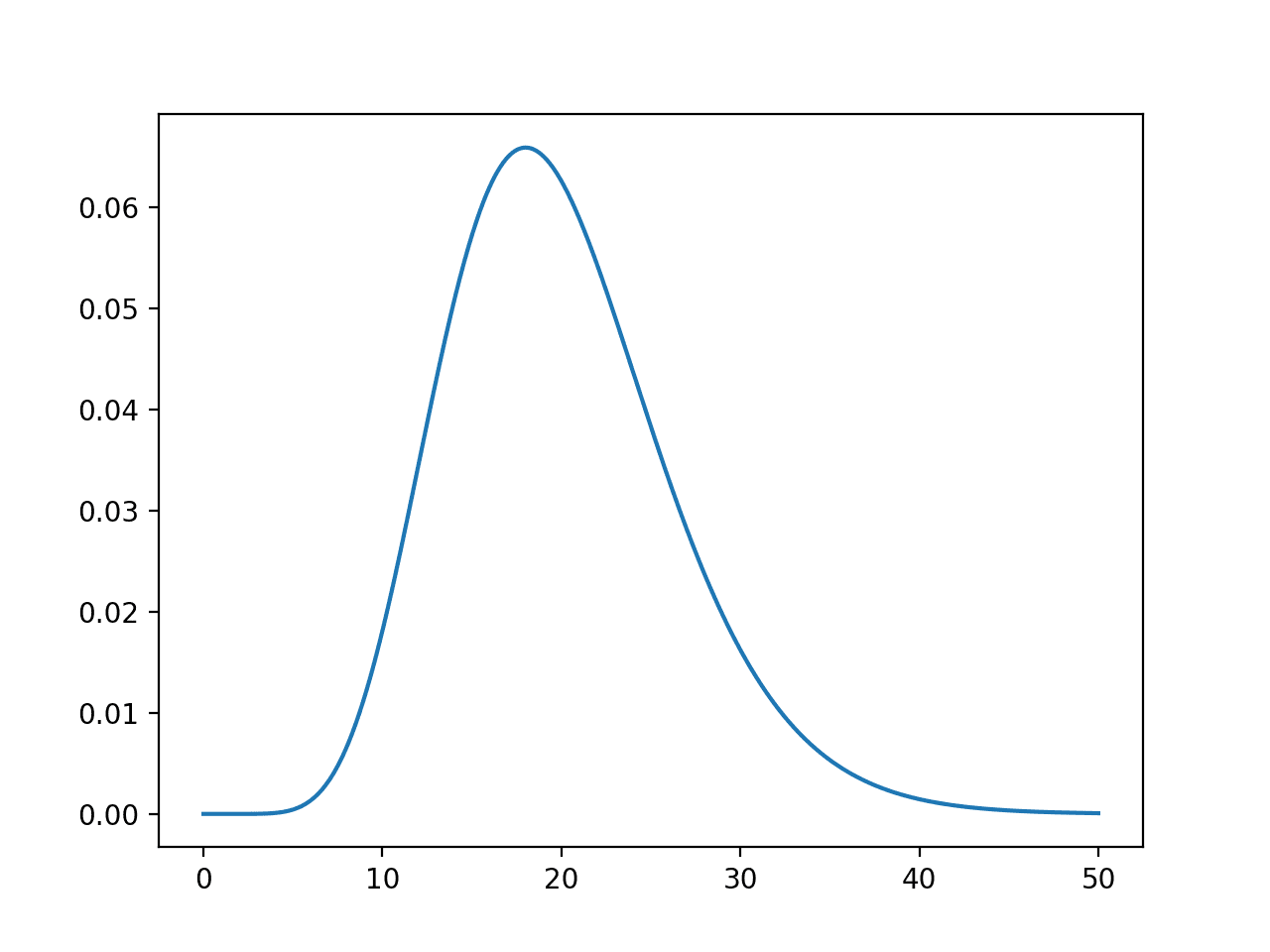
- 幂律分布。
- 帕累托分布。
一些具有著名连续概率分布的常见领域的例子包括:
- 人类身高的概率构成正态分布。
- 电影成为热门的概率构成幂律分布。
- 收入水平的概率构成帕累托分布。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 《概率论:科学的逻辑》, 2003.
- 《概率导论》,第2版,2019年。
- 《概率:写给热情的初学者》, 2016.
文章
总结
在这篇文章中,您发现了一个关于概率分布的简明介绍。
具体来说,你学到了:
- 概率论中的随机变量具有确定的定义域,可以是连续的,也可以是离散的。
- 概率分布总结了随机变量的可能值与其概率之间的关系。
- 概率密度函数或概率质量函数将值映射到概率,而累积分布函数将小于或等于某个值的结果映射到概率。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



感谢您的文章。威布尔分布在机器学习中使用吗?
什么是威布尔分布?
概率在机器学习这项先进技术中扮演着重要角色。它与微积分、代数一起,是其中的一部分。
谢谢。
Jason – 我有你的一些PDF文件,虽然我没有从头到尾读完。
你在解释机器学习概念方面真的很有天赋。
这篇文章总结了理解机器学习所需概率论的要点。
谢谢
Srini
感谢您的客气话和反馈,Srini!祝您在机器学习之旅上一帆风顺!
感谢这篇非常重要的文章。您的科普方法在完整性和对机器学习基础的重视方面令人印象深刻。
还有谁能从GAN无缝过渡到概率分布,然后再返回呢?
谢谢你,Jason。
Lorenzo Ostano
谢谢 🙂
你好,
不过我对概率分布还是很困惑。
概率分布与PMF、PDF、CDF有什么关系?
我在网上看到很多内容比较和对比均匀分布、正态分布、伯努利分布、二项分布、泊松分布等。还有很多内容比较和对比PMF、PDF、CDF。
但我找不到任何将这两者联系起来的信息。概率分布与PMF、PDF、CDF有什么关系?
谢谢。
每种类型(均匀分布、高斯分布等)都有一个PDF、CDF、PMF。
感谢对这个主题的简单解释。我需要它来更好地理解供应链物流。
诚挚地
谢谢,也许你可以从一本关于这个主题的教科书开始?
如何利用概率分布、置信区间和假设检验的概念来回答这些问题?
一家公司生产电池,其CEO声称在正常使用情况下,电池平均寿命为350小时。一位研究人员从生产线上随机抽取了20个电池进行测试。测试的电池平均寿命为320小时,标准差为50小时。
a) 构建电池寿命的95%置信区间。假设电池寿命服从正态分布。
正态分布。
b) 构建电池寿命的99%置信区间。(假设电池寿命服从正态分布是无效的)。
正态分布的假设不成立)。
c) 写下检验该声明的假设。
d) 我们是否有足够的证据表明平均寿命为350小时的声明是错误的?(在5%显著性水平下进行假设检验以检验该声明)。假设电池寿命服从正态分布。
e) 如果不能做出电池寿命服从正态分布的假设,请执行假设检验程序来检验该声明。
这看起来像是一个家庭作业问题或面试问题。我为你做这项工作是不道德的。
它通常表示为大写字母E带方括号的函数:例如,E[X]表示X的期望值或
示例,E[X] 表示 X 的期望值,或者
” E[f(x)],其中函数f()用于从X的定义域中采样一个值。”
如果X是一个随机变量,那么它包含许多事件。那么f(X)不是给我一个事件吗?
对于一个事件,只有一个概率值。
那么为什么要计算均值(E)呢?
不,f(X)给你的是事件X的概率。
***此处更正***
连续概率分布 :-
//
//
//
“概率分布函数。连续随机变量某个值的概率。”
应更正为
“PDF:概率密度函数,返回给定连续结果的概率。”
抱歉,我不确定是否同意你的用语。
非常有用的文章,为我节省了大量搜索这些信息的时间。我在哪里可以找到每种不同类型分布的具体例子?
谢谢你。
博客上有例子,例如
https://machinelearning.org.cn/discrete-probability-distributions-for-machine-learning/
很棒的文章。我正在尝试理解作为一名数据科学家,我们究竟在哪里使用概率分布?您能分享一些关于概率分布如何使用的真实世界例子吗?
最常用的一定是高斯分布。但我举一个例子来说明这为什么有用。如果你考虑一个有很多步骤的生产线,每一步都需要一些时间来完成,并且是高斯分布的。如果突然我们发现生产线变得非常慢或非常快,这正常吗?有了分布函数,我们可以计算整个过程在特定时间内完成的概率。从而判断它是否符合我们的模型(不足为奇,一切照旧)或不符合(出了问题,我们需要修正我们的工作)。