微积分是研究变化的数学分支。
微积分解决复杂但连续问题的有效性在于它能够将问题分解成无限多个更简单的部分，分别解决它们，然后将它们重新组合成原始的整体。这种策略可以应用于研究所有能够以这种方式分解的连续元素，无论是几何形状的曲率，还是飞行中物体的轨迹，或时间间隔。
在本教程中，您将了解微积分的起源及其应用。
完成本教程后，您将了解：
- 什么是微积分？
- 微积分如何应用于现实世界？
让我们开始吧。
什么是微积分？
照片由 Stephen Lammens 拍摄，保留部分权利。
教程概述
本教程分为两部分；它们是
- 微积分
- 微积分的应用
微积分
Calculus 是拉丁语，意为石头或卵石。
这个词的使用从古老的用小石头进行计算（如加法和乘法）的实践中渗透到数学中。虽然这个词的使用随着时间从许多计算方法的名称中消失了，但一个重要的数学分支保留了它，以至于我们现在将其称为 The Calculus。
微积分，像其他形式的数学一样，不仅仅是一种语言；它也是一个极其强大的推理系统。
—— 摘自《无限的力量》，2019年，第xii页。
微积分从几何学中发展而来。
最初，几何学关注直线、平面和角度，反映了其在建造坡道和金字塔等方面的实用起源。然而，几何学家发现他们缺乏工具来研究圆形、球体、圆柱体和圆锥体。这些弯曲形状的表面积和体积比由直线和平面组成的直线形状更难分析。尽管微积分以复杂著称，但它源于对简化的追求，通过将复杂问题分解为更简单的部分。
大约在公元前250年，古希腊有一个致力于曲线奥秘的数学小创业公司。
—— 摘自《无限的力量》，2019年，第3页。
为此，微积分围绕着对无限的受控使用，将其作为曲线与直线之间的桥梁。
无限原理
为了阐明任何连续的形状、物体、运动、过程或现象——无论它看起来多么狂野和复杂——将其重新想象成无限系列更简单的部分，分析这些部分，然后将结果加在一起，以理解原始的整体。
—— 摘自《无限的力量》，2019年，第xvi页。
为了更好地理解这个概念，想象一下你乘坐宇宙飞船前往月球。当你从地球望向月球时，它的轮廓无疑是弯曲的。但当你靠近，轮廓的更小部分开始填满观察窗时，曲率变得平缓且不那么明显。最终，曲率变得如此之小，以至于轮廓的无限小部分看起来像一条直线。如果我们将月球的圆形形状沿其无限小的轮廓部分切片，然后将这些无限小的切片排列成一个矩形，那么我们就可以计算出它的面积：通过将其宽度乘以高度。
这就是微积分的精髓：如果通过显微镜观察一个弯曲的形状，被放大部分的曲率将显得笔直而平坦，这一突破使得分析弯曲形状成为可能，原则上是通过将许多直线部分组合起来。
因此，微积分可以被认为包含两个阶段：切割和重建。
用数学术语来说，切割过程总是涉及无限精细的减法，用于量化部分之间的差异。因此，这部分主题被称为微分学。重组过程总是涉及无限加法，将各部分重新整合回原始整体。这部分主题被称为积分学。
—— 摘自《无限的力量》，2019年，第xv页。
考虑到这一点，让我们回顾一下我们的简单例子。
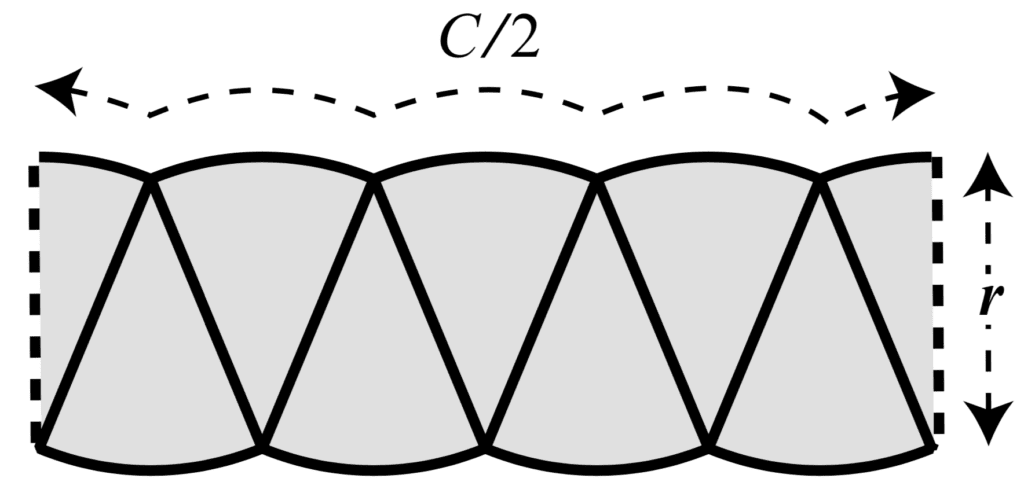
假设我们已将月球的圆形形状切成小块，并将这些小块并排放置。
我们形成的形状类似于一个矩形，其宽度等于圆周的一半，C/2，高度等于圆的半径，r。
将圆的切片重新排列成矩形
摘自《无限的力量》。
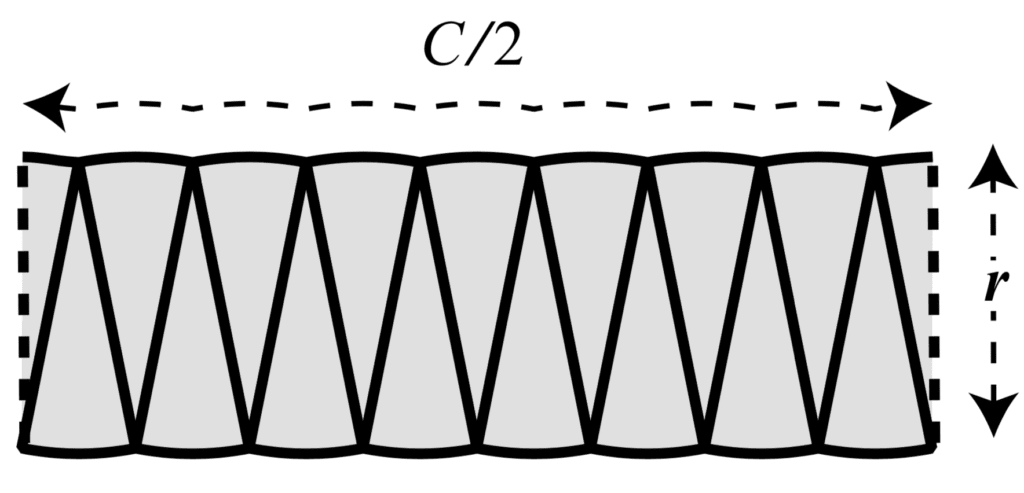
为了进一步平坦化曲率，我们可以将圆形切成更薄的片。
将更薄的圆片重新排列成矩形
摘自《无限的力量》。
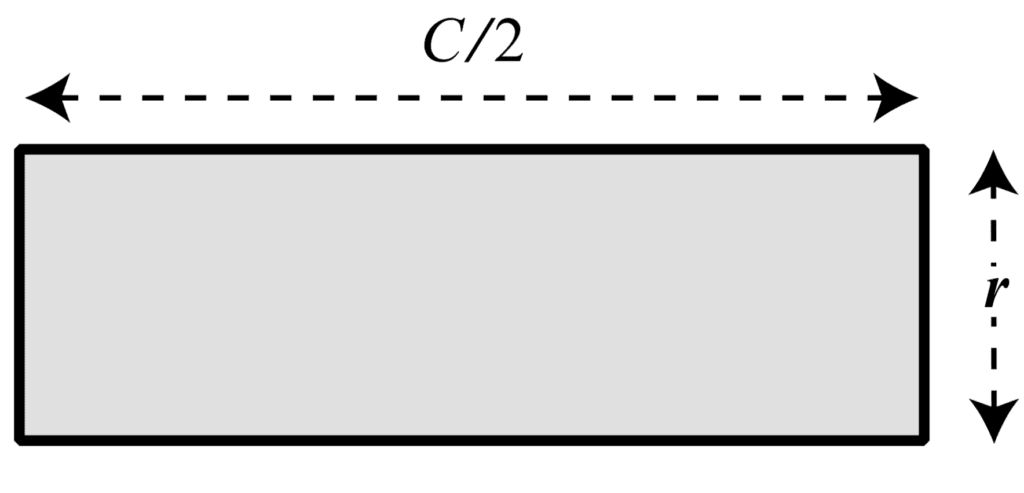
切片越薄，曲率越平坦，直到我们达到无限多个切片的极限，此时形状变得完全矩形。
将无限薄的圆片重新排列成矩形
摘自《无限的力量》。
我们从圆形中切割出切片，并将它们重新排列成矩形并不会改变它们的面积。因此，计算圆的面积等同于计算所得矩形的面积：A = rC/2。
曲线不仅是几何形状的特征，也以抛物线轨迹（由抛射物描绘）或行星绕太阳的椭圆轨道等形式出现在自然界中。
于是，第二个巨大的痴迷开始了：对地球和太阳系运动奥秘的迷恋。
—— 摘自《无限的力量》，2019年，第xix页。
伴随着曲线和运动，下一个自然而然的问题是它们的变化率。
曲线和运动的奥秘解决后，微积分转向了它的第三个毕生痴迷：变化的奥秘。
—— 摘自《无限的力量》，2019年，第xxii页。
正是通过应用无限原理，微积分才允许我们通过将其近似为许多无限小步来研究运动和变化。
正是因为这个原因，微积分被认为是宇宙的语言。
微积分的应用
微积分已应用于许多领域，从牛顿在解决数学物理问题中的应用，到最近牛顿思想在NASA数学家凯瑟琳·约翰逊及其同事工作中的应用。
在19世纪60年代，詹姆斯·克拉克·麦克斯韦利用微积分重新阐述了电磁学的实验定律，最终不仅预测了电磁波的存在，还揭示了光作为电磁波的本质。基于他的工作，尼古拉·特斯拉创建了第一个无线电通信系统，古格列尔莫·马可尼传输了第一批无线电报，最终许多现代设备，如电视和智能手机，应运而生。
1917年，阿尔伯特·爱因斯坦也将微积分应用于原子跃迁模型，以预测受激发射效应。他的工作后来促成了20世纪60年代第一个实用激光器的诞生，此后激光器被用于许多不同的设备，如CD播放器和条形码扫描仪。
没有微积分，我们就不会有手机、电脑或微波炉。我们不会有广播。或电视。或孕妇用的超声波，或迷路旅客用的GPS。我们不会分裂原子，不会解开人类基因组，也不会把宇航员送上月球。我们甚至可能没有《独立宣言》。
—— 摘自《无限的力量》，2019年，第vii页。
更有趣的是微积分在机器学习中的重要作用。它是梯度下降等重要算法的基础，这些算法需要计算函数的梯度，并且通常对训练机器学习模型至关重要。这使得微积分成为机器学习中基本的数学工具之一。
进一步阅读
如果您想深入了解，本节提供了更多关于该主题的资源。
书籍
文章
总结
在本教程中，您了解了微积分的起源及其应用。
具体来说，你学到了：
- 微积分是研究变化的数学分支，其基础是切割和重建策略。
- 微积分促成了许多发现和许多我们所知的现代设备的创造，它也是机器学习中一个基本的数学工具。
你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。
我一直对微积分很着迷。谢谢 Stefania 的精彩解释。
不客气！
微积分是如何给我们带来《独立宣言》的？
据我记忆，这是本杰明·富兰克林的一段引文。你可能需要读一下那本书。
这本书在第239页再次提到了这一点。
好文章，谢谢 Stefania
对微积分及其应用以及对我们日常生活的贡献的精彩描述。
不客气！
微积分对我们的日常生活有多大的贡献？
嗨，阿卜杜勒……以下内容可能对您有帮助
https://allusesof.com/math/51-amazing-uses-of-calculus-in-real-life/