我们之前已经看到，微积分是机器学习中的核心数学概念之一，它使我们能够理解各种机器学习算法的内部工作原理。
而微积分又建立在代数和几何学的几项基本概念之上。当我们深入学习微积分的更高级主题时，例如极限的评估和导数的计算（仅举几例），拥有这些基础知识的重要性将更加凸显。
在本教程中，您将了解有助于您学习微积分的几项预备知识。
完成本教程后，您将了解：
- 线性函数和非线性函数是微积分和机器学习的核心，许多微积分问题都涉及它们的运用。
- 代数和三角学的基本概念为微积分奠定了基础，并且在我们将要学习更高级的微积分主题时，它们将变得尤其重要。
让我们开始吧。
在开始之前你需要了解什么：微积分先决条件的简要介绍
摄影：Dino Reichmuth，部分版权保留。
教程概述
本教程分为三个部分；它们是：
- 函数的概念
- 预代数和代数基础
- 三角学基础
函数的概念
函数是定义因变量和自变量之间关系的规则。
例子随处可见：您所在城市的全年平均气温取决于一年中的时间，并且是时间的函数；物体下落的距离是自其下落以来所经过时间的函数；圆的面积是其半径的函数；封闭气体的压力是其温度的函数。
——《傻瓜的微积分》，2016年，第43页。
在机器学习中，神经网络通过一个函数来学习，这个函数可以表示输入特征（自变量）与期望输出（因变量）之间的关系。在这种情况下，学习到的函数定义了输入值与一个或多个输出值之间的确定性映射。我们可以将这种映射表示如下：
输出(s) = 函数(输入)
更正式地说，函数通常表示为 *y* = *f*(*x*)，这可以理解为 *y* 是 *x* 的函数。这种表示法指定 *x* 是我们已知的自变量输入，而 *y* 是我们希望找到的因变量输出。例如，如果我们考虑平方函数 *f*(*x*) = *x*²，那么输入 3 将产生输出 9
*y* = *f*(3) = 9
函数还可以通过在 *x*–*y* 坐标平面上的*图形*来直观地表示。
函数 f 的图形是指所有点 (x, f(x)) 的集合。
——《微积分漫游指南》，2019年，第13页。
在绘制函数图形时，自变量输入放在 *x* 轴上，因变量输出放在 *y* 轴上。图形有助于更好地说明自变量和因变量之间的关系：图形（因此，关系）是上升还是下降，以及以何种速率？
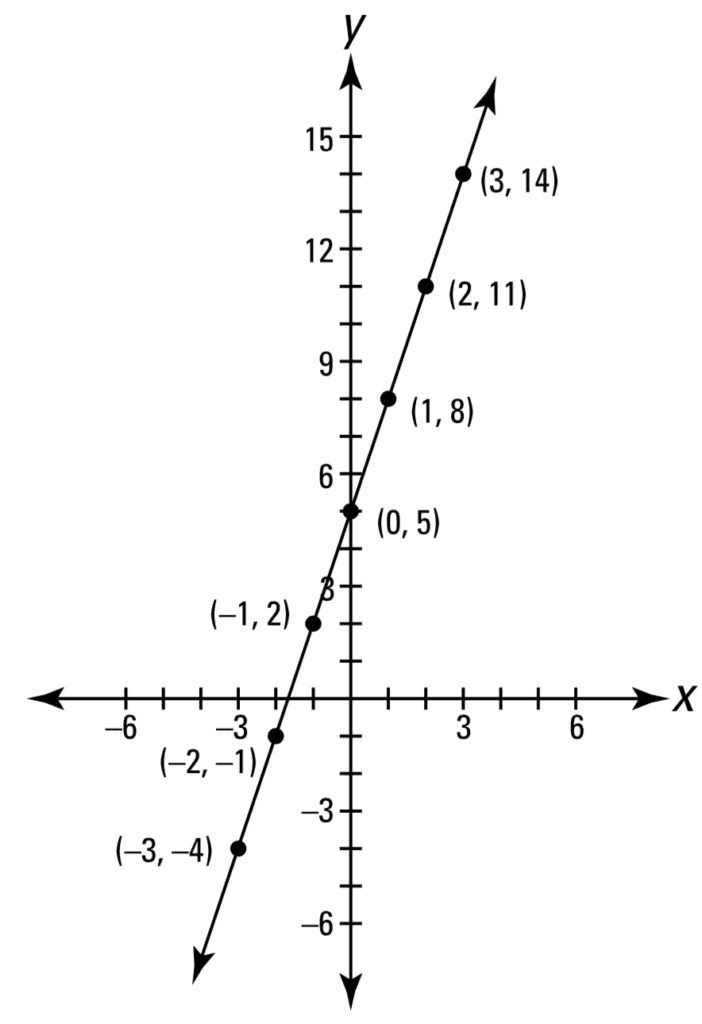
直线是在坐标平面上可以绘制的最简单的函数之一。以直线 *y* = 3*x* + 5 的图形为例：
线性函数的折线图
摘自《傻瓜的微积分》
这条直线可以用*线性*函数来描述，之所以称为线性函数，是因为输出随着输入的任何变化而按比例变化。描述这条直线的线性函数可以用斜截式表示，其中斜率用 *m* 表示，*y* 轴截距用 *c* 表示：
*f*(*x*) = *mx* + *c* = 3*x* + 5
在讨论变化率时，我们已经了解了如何计算斜率。
如果我们考虑将斜率设为零的特殊情况，则产生的水平线将由以下形式的*常数*函数描述：
*f*(*x*) = *c* = 5
在机器学习的背景下，这种线性函数定义的计算由神经网络中的每个神经元实现。具体来说，每个神经元接收来自前一层神经元或训练数据的 *n* 个输入 *x*ᵢ，并计算这些输入的加权和（其中*权重* *w*ᵢ 是机器学习中斜率 *m* 的更常用术语），以产生输出 *z*：
输入的加权和
摘自《深度学习》
训练神经网络的过程涉及学习最能表示输入数据集模式的权重，这个过程由梯度下降算法执行。
除了线性函数，还有另一类*非线性*函数。
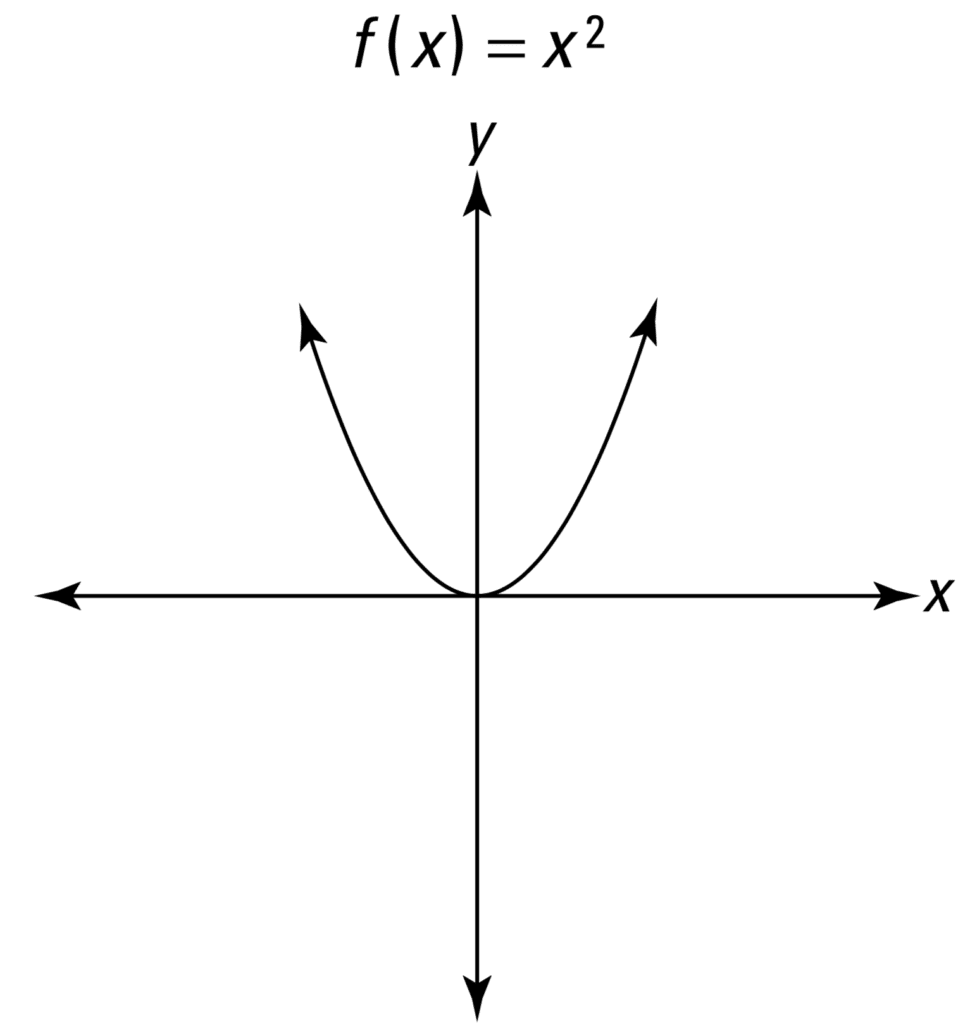
所有非线性函数中最简单的可以说是抛物线，它可以用以下方式描述：
*y* = *f*(*x*) = *x*²
当绘制图形时，我们会发现这是一个偶函数，因为它关于 *y* 轴对称，并且从不在 *x* 轴下方。
抛物线的折线图
摘自《傻瓜的微积分》
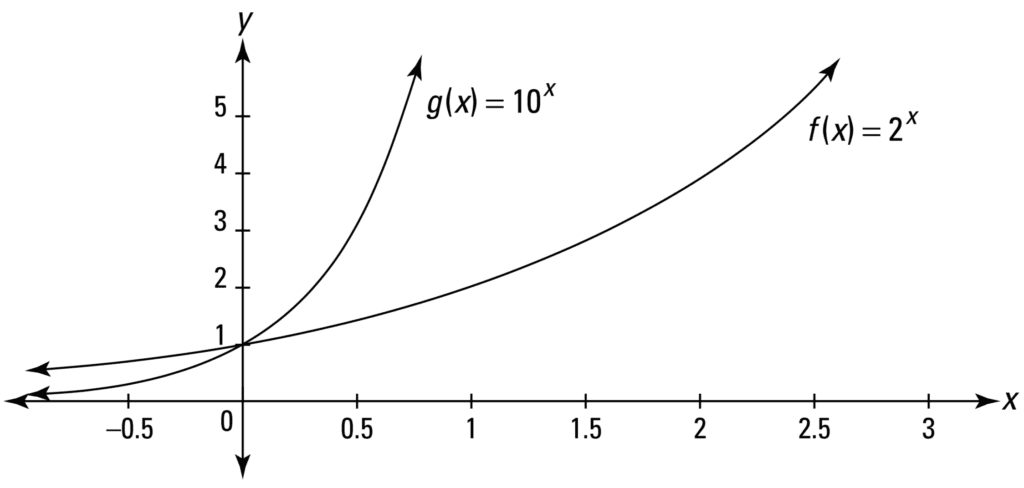
尽管如此，非线性函数可以有多种不同的形状。例如，考虑指数函数 *f*(*x*) = *b*ˣ，它根据 *x* 的值无限增长或衰减，或*单调*变化。
指数函数的折线图
摘自《傻瓜的微积分》
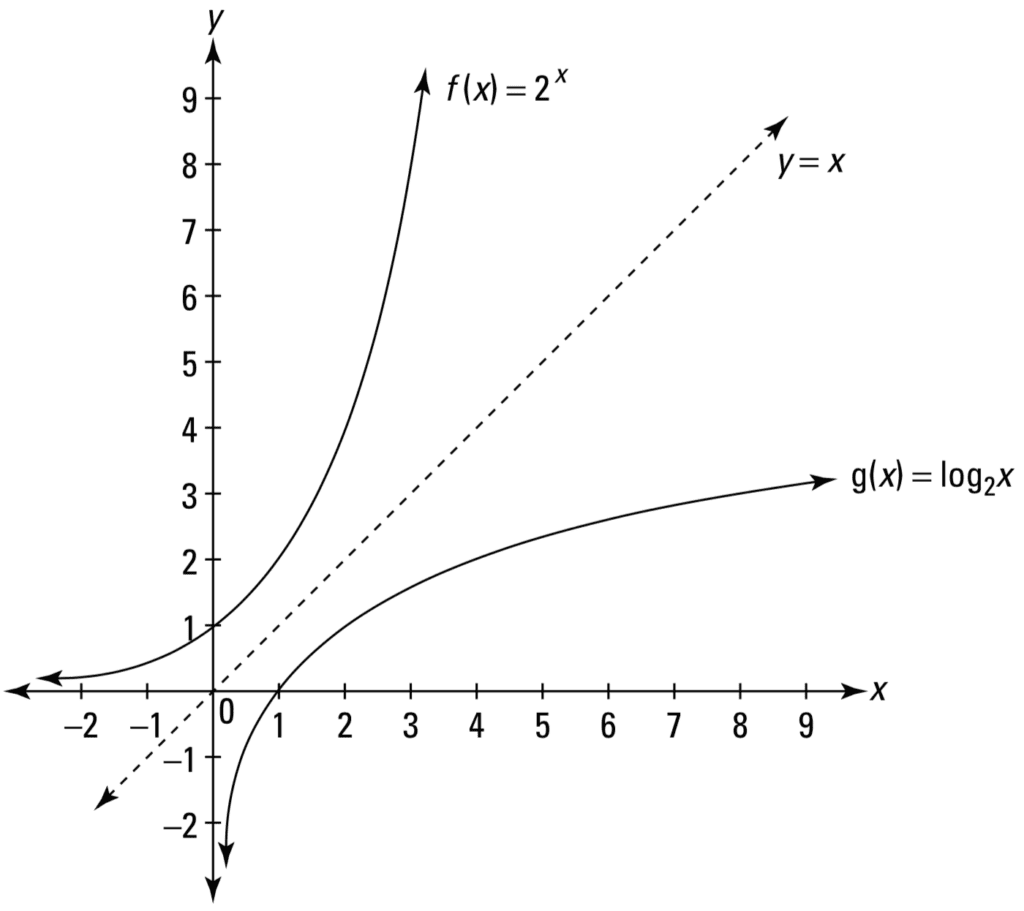
或者对数函数 *f*(*x*) = log₂ *x*，它与指数函数类似，但 *x*– 和 *y*– 轴互换了。
对数函数的折线图
摘自《傻瓜的微积分》
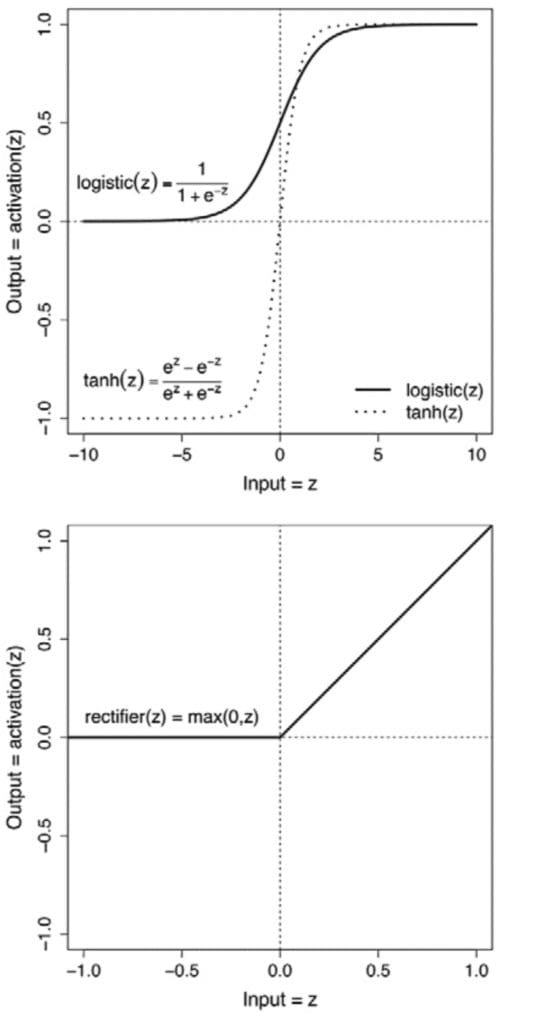
对于深度学习尤其重要的是逻辑函数、tanh 函数和 ReLU (Rectified Linear Units) 非线性函数，它们作为*激活函数*。
逻辑函数、Tanh 和 ReLU 函数的折线图
摘自《深度学习》
这些激活函数的重要性在于它们将非线性映射引入神经元的处理过程中。如果我们仅依赖每个神经元通过线性回归计算输入的加权和，那么我们将仅限于学习从输入到输出的线性映射。然而，许多现实世界的关系比这要复杂得多，线性映射无法准确地模拟它们。在神经元的输出 *z* 中引入非线性，可以使神经网络模拟这种非线性关系。
输出 = 激活函数(*z*)
…… 神经元，作为神经网络和深度学习的基本构建块，由一个简单的两步操作序列定义：计算加权和，然后将结果通过激活函数。
——《深度学习》，2019年，第76页。
在神经网络的训练过程中，非线性函数也以误差函数的形式出现。
在计算预测值和目标输出值之间的误差时，随着模型权重的变化，可以生成非线性误差函数。其形状可以像抛物线一样简单，但大多数情况下，它具有许多局部最小值和鞍点。梯度下降算法通过计算在特定实例中触及曲线的*切线*的斜率来下降这个非线性误差函数：这是微积分中的另一个重要概念，它允许我们通过将复杂的曲线函数分解为许多沿着一侧排列的无穷小的直线段来分析它们。
预代数和代数基础
代数是微积分的重要基础之一。
代数是微积分的语言。不懂代数就无法学习微积分，就像不懂中文就无法写中国诗一样。
——《傻瓜的微积分》，2016年，第29页。
代数中有几个基本概念对微积分非常有用，例如关于分数、幂、平方根和对数。
让我们先回顾一下分数的基本运算。
- 除以零：分母永远不能等于零。例如，像 5/0 这样的分数结果是未定义的。其背后的直观理解是，您永远无法用分母中的零乘以分子中的值来得到结果。
- 倒数：分数的倒数是它的乘法逆元。简单来说，求分数的倒数就是将它上下颠倒。因此，例如 3/4 的倒数变为 4/3。
- 分数乘法：分数之间的乘法就像分子相乘，分母相乘一样简单：
(a / b) * (c / d) = ac / bd
- 分数除法：分数除法与乘法非常相似，但有一个额外的步骤：在相乘之前先求第二个分数的倒数。因此，再次考虑两个通用分数：
(a / b) ÷ (c / d) = (a / b) * (d / c) = ad / bc
- 分数加法：一个重要的第一步是找到所有要相加的分数之间的公分母。任何公分母都可以，但我们通常找到*最小*公分母。找到最小公分母有时就像将所有单个分母相乘一样简单：
(a / b) + (c / d) = (ad + cb) / bd
- 分数减法：分数减法的过程与分数加法类似：
(a / b) – (c / d) = (ad – cb) / bd
- 分数约分：对于分子和分母中具有不间断乘法链的分数，可以通过约去出现在分子和分母中的任何公因子来简化：
a³b² / ac = a²b² / c
微积分的下一个重要预备知识是关于指数，或者通常称为幂。在处理幂时也有几个规则需要记住。
- 零次幂：任何数（有理数或无理数，负数或正数，*除了*零本身）的零次幂都等于一：
x⁰ = 1
- 负数幂：底数为负数次幂的数会变成一个分数，但符号不变：
x⁻ᵃ = 1 / xᵃ
- 分数幂：底数为分数次幂的数可以转换为根式运算：
xᵃ/ᵇ = (ᵇ√x)ᵃ = ᵇ√xᵃ
- 幂的加法：如果两个（或更多）*相同*的底数相乘，则它们的幂可以相加：
xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾
- 幂的减法：同样，如果两个相同的底数相除，则它们的幂可以相减：
xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾
- 幂的乘方：如果一个幂还被提升到另一个幂，则这两个幂可以相乘：
(xᵃ)ᵇ = x⁽ᵃᵇ⁾
- 幂的分配：无论底数是相乘还是相除，幂都可以分配到每个变量上。但是，如果底数是相加或相减，则*不能*分配：
(xyz)ᵃ = xᵃ yᵃ zᵃ
(x / y)ᵃ = xᵃ / yᵃ
类似地，我们也有关于根式运算的规则和关于对数运算的规则。
根式性质
摘自《傻瓜的微积分》
对数性质
摘自《傻瓜的微积分》
最后，知道如何解一元二次方程在微积分中也很有用。
如果一元二次方程可以因式分解，那么最简单的解法是将其写成乘积形式。例如，以下一元二次方程可以因式分解如下：
x² – 9 = (x + 3)(x – 3) = 0
将每个因子设为零，我们可以找到该方程的解，在这种情况下是 *x* = ±3。
或者，可以使用以下一元二次方程求根公式：
一元二次方程求根公式
摘自《傻瓜的微积分》
如果我们考虑与上面相同的一元二次方程，那么我们将系数设置为 *a* = 1、*b* = 0 和 *c* = 9，这将再次得到 *x* = ±3 作为我们的解。
三角学基础
三角学围绕三个主要三角函数，即正弦、余弦和正切，以及它们的倒数，即余割、正割和余切。
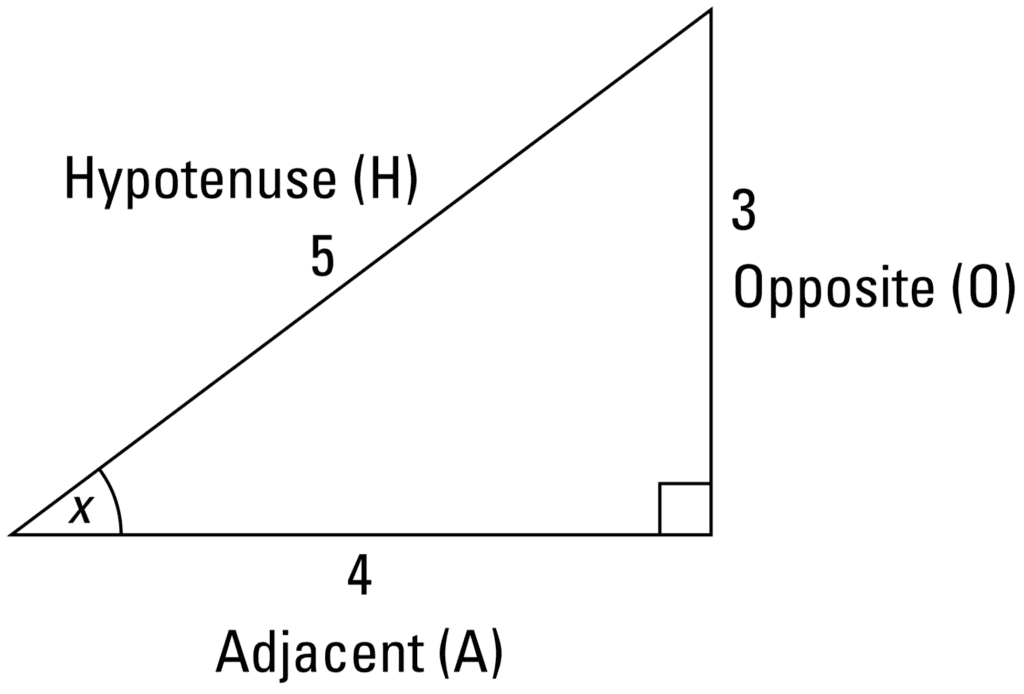
当应用于直角三角形时，这三个主要函数允许我们计算边的长度，或三角形的另外两个锐角，具体取决于我们最初拥有的信息。具体来说，对于以下 3-4-5 三角形中的某个角度 *x*：
3-4-5 三角形
摘自《傻瓜的微积分》
三个主要三角函数
摘自《傻瓜的微积分》
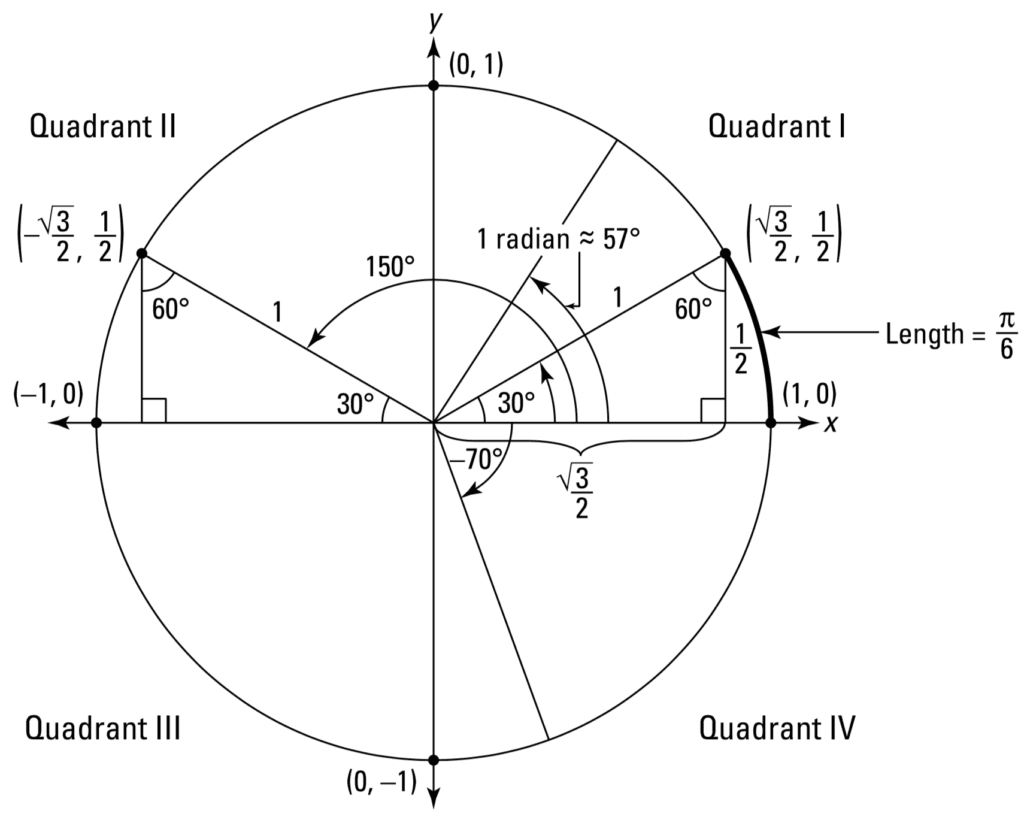
正弦、余弦和正切函数仅适用于直角三角形，因此只能用于计算小于 90° 的锐角。尽管如此，如果我们要在 *x*–*y* 坐标平面上的*单位圆*内工作，我们就可以将三角学应用于 0° 到 360° 之间的所有角度。
单位圆
摘自《傻瓜的微积分》
单位圆的圆心位于 *x*–*y* 坐标平面的原点，半径为一单位。围绕单位圆的旋转从正 *x* 轴开始，沿逆时针方向进行。然后，旋转角度的余弦由撞击单位圆的点 *x* 坐标给出，而 *y* 坐标指定了旋转角度的正弦。还值得注意的是，象限是对称的，因此一个象限中的点在其他三个象限中也有对称的对应点。
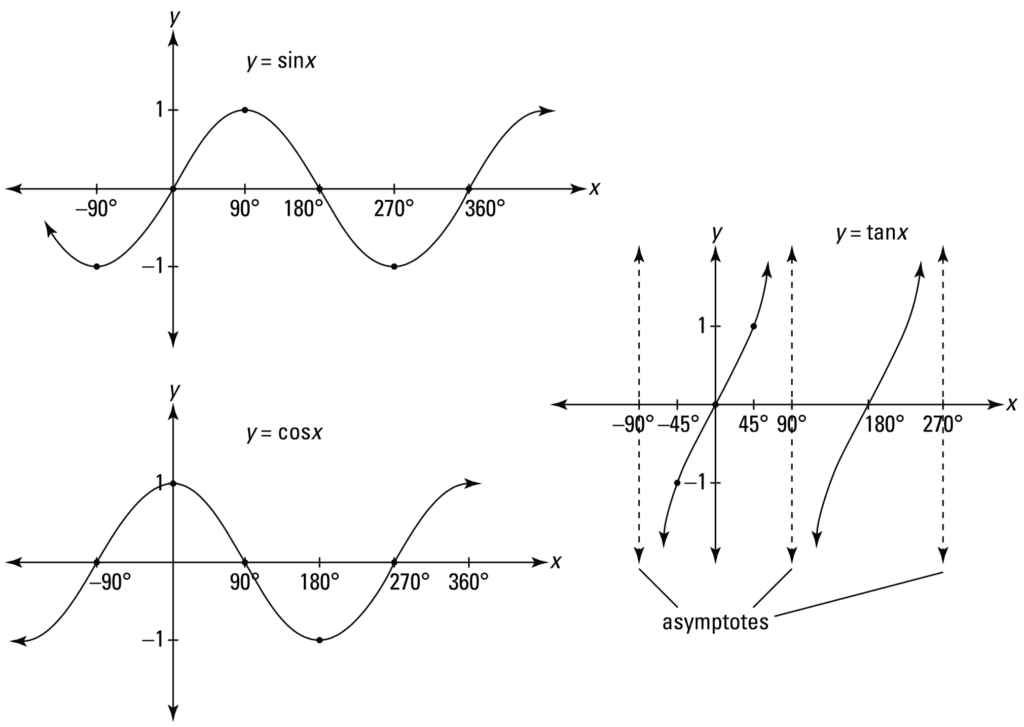
绘制的正弦、余弦和正切函数如下所示：
正弦、余弦和正切函数的折线图
摘自《傻瓜的微积分》
所有函数都是周期性的，正弦和余弦函数具有相同的形状，但它们之间相隔 90°。正弦和余弦函数确实可以根据围绕单位圆旋转的计算出的 *x*– 和 *y* 坐标轻松绘制。正切函数也可以类似地绘制，因为对于任何角度 θ，该函数都可以定义为：
tan θ = sin θ / cos θ = *y* / *x*
正切函数在 ±90° 时是未定义的，因为该角度的余弦值为零。因此，我们在这些角度绘制垂直*渐近线*，这些是曲线接近但从不触及的虚线。
最后一点是关于这些三角函数的反函数。以正弦函数为例，其反函数表示为 sin⁻¹。这不应与余割函数混淆，余割函数是正弦的*倒数*，因此与它的反函数不同。
进一步阅读
如果您想深入了解，本节提供了更多关于该主题的资源。
书籍
总结
在本教程中，您了解了微积分的几项预备知识。
具体来说，你学到了：
- 线性函数和非线性函数是微积分和机器学习的核心，许多微积分问题都涉及它们的运用。
- 代数和三角学的基本概念为微积分奠定了基础，并且在我们将要学习更高级的微积分主题时，它们将变得尤其重要。
你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。
您的分数幂图示不正确：您需要交换 a 和 b。
是的，谢谢您指出这一点！这在我校对时遗漏了。
非常感谢 Stefania；在我学术/职业生涯的关键时刻，这篇文章写得太好了！