链式法则允许我们找到复合函数的导数。
反向传播算法广泛使用链式法则来训练前馈神经网络。通过以高效的方式应用链式法则并遵循特定的操作顺序,反向传播算法计算损失函数相对于网络中每个权重的误差梯度。
在本教程中,您将了解单变量和多变量函数的微积分链式法则。
完成本教程后,您将了解:
- 复合函数是两个(或更多)函数的组合。
- 链式法则允许我们找到复合函数的导数。
- 链式法则可以推广到多变量函数,并用树状图表示。
- 反向传播算法广泛应用链式法则,以计算损失函数相对于每个权重的误差梯度。
让我们开始吧。

单变量和多变量函数的链式法则
图片来源:Pascal Debrunner,保留部分权利。
教程概述
本教程分为四个部分;它们是
- 复合函数
- 链式法则
- 广义链式法则
- 在机器学习中的应用
先决条件
对于本教程,我们假设您已经了解以下内容:
您可以通过点击上面给出的链接来复习这些概念。
复合函数
到目前为止,我们已经遇到过单变量和多变量函数(分别称为单变量函数和多变量函数)。我们现在将它们扩展到它们的复合形式。我们最终将看到如何应用链式法则来求它们的导数,但稍后会详细介绍。
复合函数是两个函数的组合。
——第49页,《傻瓜微积分》,2016年。
考虑两个单自变量函数,f(x) = 2x – 1 和 g(x) = x3。它们的复合函数可以定义如下:
h = g(f(x))
在这个操作中,g 是 f 的函数。这意味着 g 作用于函数 f 作用于 x 的结果,从而产生 h。
让我们使用上面指定的函数来考虑一个具体的例子,以便更好地理解。
假设 f(x) 和 g(x) 是两个级联系统,接收输入 x = 5
由于 f(x) 是级联中的第一个系统(因为它在复合函数中是内部函数),其输出首先计算出来:
f(5) = (2 × 5) – 1 = 9
然后将此结果作为输入传递给 g(x),即级联中的第二个系统(因为它在复合函数中是外部函数),以产生复合函数的最终结果:
g(9) = 93 = 729
我们也可以一次性计算出最终结果,如果执行以下计算:
h = g(f(x)) = (2x – 1)3 = 729
函数组合也可以被认为是链接过程,用一个更熟悉的术语来说,其中一个函数的输出作为链中下一个函数的输入。
对于复合函数,顺序很重要。
——第49页,《傻瓜微积分》,2016年。
请记住,函数组合是一个非交换过程,这意味着在级联(或链)中交换 f(x) 和 g(x) 的顺序不会产生相同的结果。因此:
g(f(x)) ≠ f(g(x))
函数的组合也可以扩展到多变量情况
h = g(r, s, t) = g(r(x, y), s(x, y), t(x, y)) = g(f(x, y))
这里,f(x, y) 是一个有两个自变量(或输入)x 和 y 的向量值函数。它由三个分量(对于这个特定示例)组成,即 r(x, y)、s(x, y) 和 t(x, y),它们也称为 f 的分量函数。
这意味着 f(x, y) 会将两个输入映射到三个输出,然后将这三个输出输入到链中的下一个系统 g(r, s, t) 中,以生成 h。
想开始学习机器学习微积分吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
链式法则
链式法则允许我们找到复合函数的导数。
首先,我们来定义链式法则如何对复合函数求导,然后将其分解为独立的组成部分以便更好地理解。如果再次考虑复合函数 h = g(f(x)),那么其由链式法则给出的导数为:
这里,u 是内部函数 f 的输出(因此,u = f(x)),然后将其作为输入传递给下一个函数 g 以产生 h(因此,h = g(u))。因此,请注意链式法则如何通过中间变量 u 将最终输出 h 与输入 x 联系起来。
回想一下,复合函数的定义如下:
h(x) = g(f(x)) = (2x – 1)3
链式法则的第一个组成部分,dh / du,告诉我们首先找到复合函数外部部分的导数,同时忽略内部的任何内容。为此,我们将应用幂法则:
((2x – 1)3)’ = 3(2x – 1)2
然后将结果乘以链式法则的第二个组成部分,du / dx,这是复合函数内部部分的导数,这次忽略外部的任何内容:
( (2x – 1)’ )3 = 2
由链式法则定义的复合函数的导数如下:
h’ = 3(2x – 1)2 × 2 = 6(2x – 1)2
我们在这里考虑了一个简单的例子,但将链式法则应用于更复杂函数的概念保持不变。我们将在单独的教程中考虑更具挑战性的函数。
广义链式法则
我们可以将链式法则推广到单变量之外的情况。
考虑 x ∈ ℝm 和 u ∈ ℝn 的情况,这意味着内部函数 f 将 m 个输入映射到 n 个输出,而外部函数 g 接收 n 个输入以产生一个输出 h。对于 i = 1, …, m,广义链式法则指出:
或者以更紧凑的形式,对于 j = 1, …, n
请记住,在求多变量函数的梯度时,我们使用偏导数。
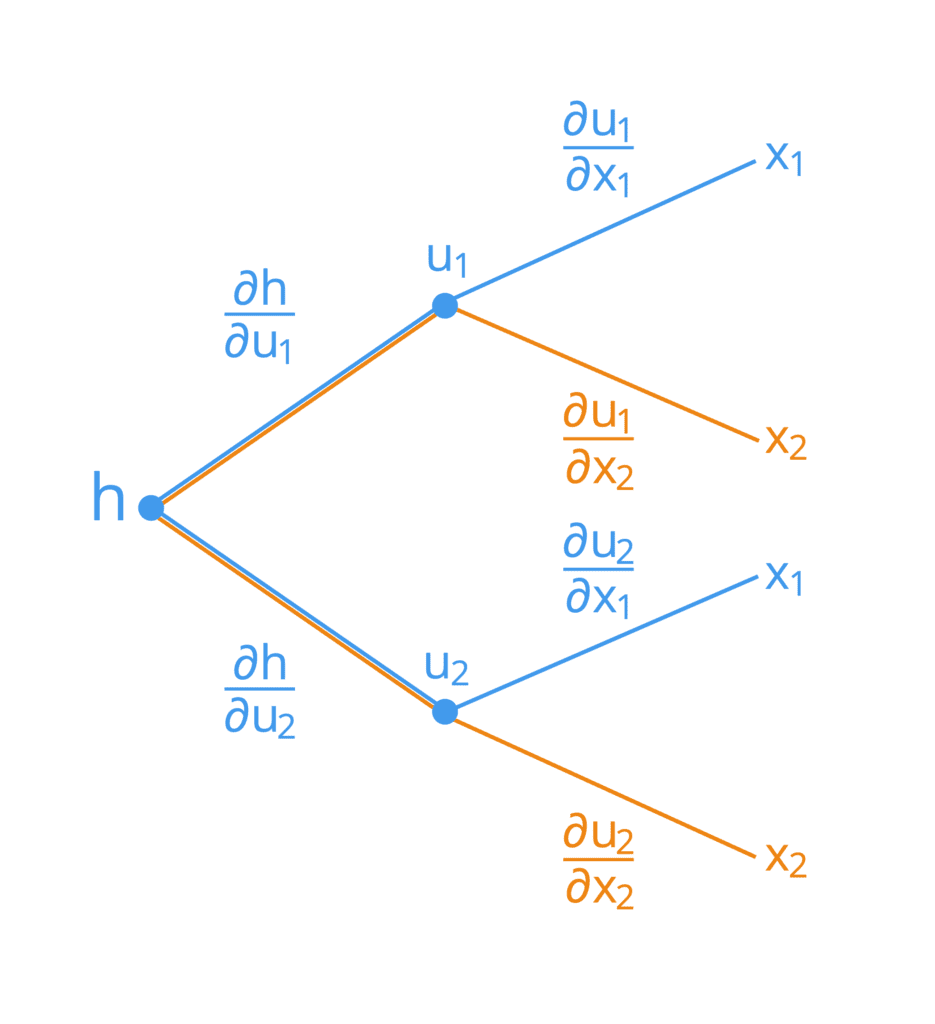
我们还可以通过树状图来可视化链式法则的运作。
假设我们有一个两个自变量 x1 和 x2 的复合函数,定义如下:
h = g(f(x1, x2)) = g(u1(x1, x2), u2(x1, x2))
这里,u1 和 u2 作为中间变量。它的树状图表示如下:
为了推导出每个输入 x1 和 x2 的公式,我们可以从树状图的左侧开始,并沿着其分支向右。通过这种方式,我们发现我们形成了以下两个公式(为简单起见,已将求和的分支进行了颜色编码):
请注意链式法则如何通过中间变量 uj 将最终输出 h 与每个输入 xi 相关联。这是反向传播算法广泛应用于优化神经网络权重的一个概念。
在机器学习中的应用
观察树状图与神经网络的典型表示多么相似(尽管我们通常将后者表示为将输入放在左侧,输出放在右侧)。我们可以通过使用反向传播算法将链式法则应用于神经网络,其方式与我们上面将其应用于树状图的方式非常相似。
链式法则被极致使用的领域是深度学习,其中函数值 y 被计算为多层函数组合。
——第159页,《机器学习数学》,2020年。
神经网络确实可以用一个巨大的嵌套复合函数来表示。例如:
y = fK ( fK – 1 ( … ( f1(x)) … ))
这里,x 是神经网络的输入(例如图像),而 y 是输出(例如类别标签)。每个函数 fi,对于 i = 1, …, K,都有其自身的权重。
将链式法则应用于这样的复合函数,使我们能够反向通过构成神经网络的所有隐藏层,并有效地计算损失函数相对于网络中每个权重 wi 的误差梯度,直到我们到达输入层。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 微积分傻瓜书, 2016.
- 单变量和多变量微积分, 2020.
- 深度学习, 2017.
- 机器学习数学, 2020.
总结
在本教程中,您了解了微积分中单变量和多变量函数的链式法则。
具体来说,你学到了:
- 复合函数是两个(或更多)函数的组合。
- 链式法则允许我们找到复合函数的导数。
- 链式法则可以推广到多变量函数,并用树状图表示。
- 反向传播算法广泛应用链式法则,以计算损失函数相对于每个权重的误差梯度。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。
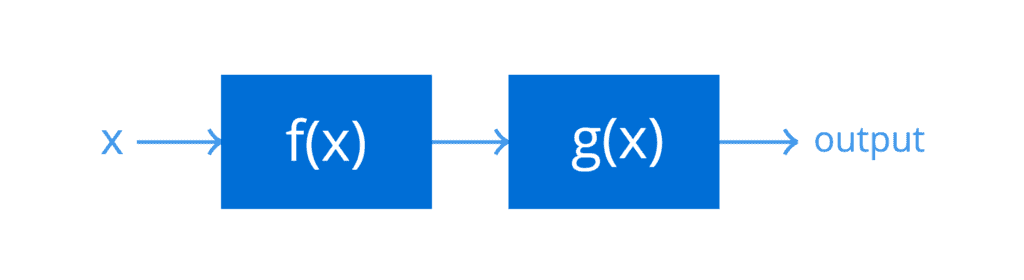
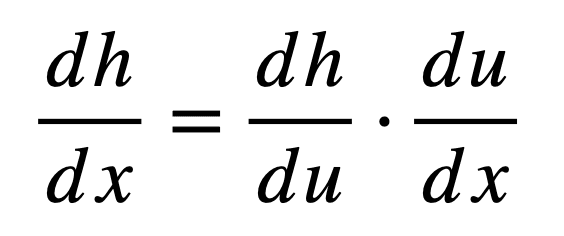
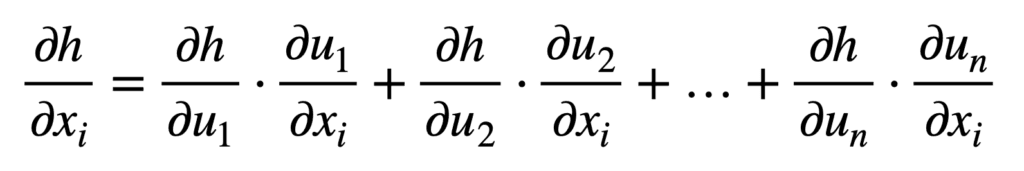
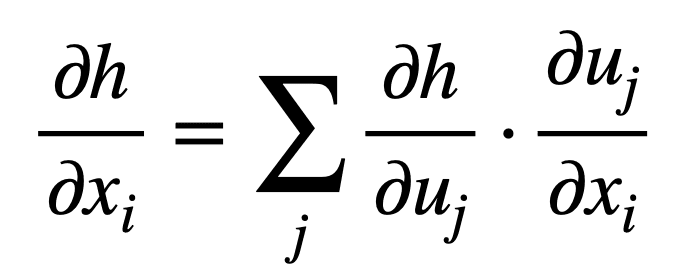
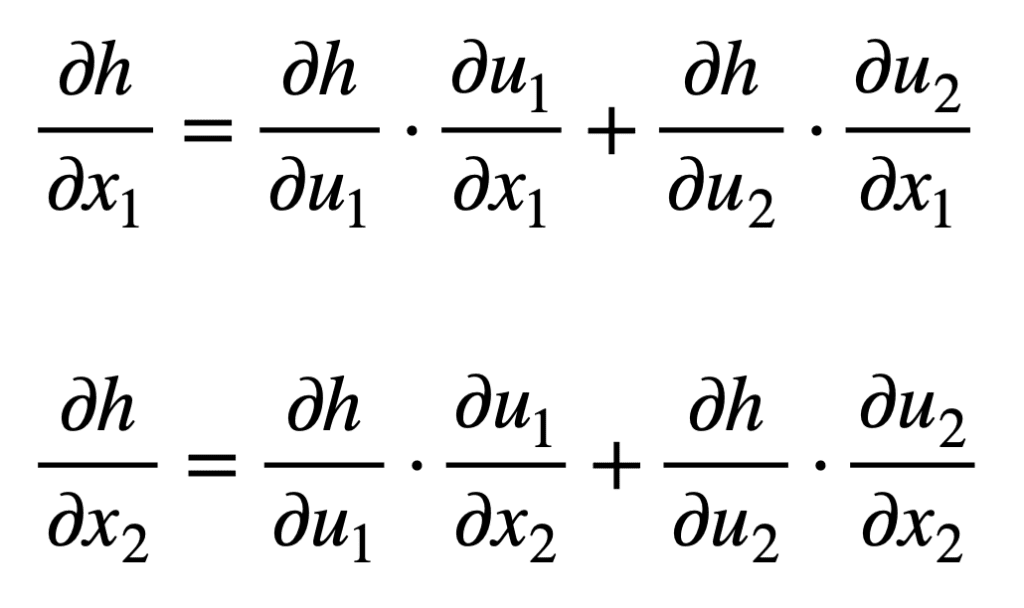







以至仁至慈的真主之名
如此美丽,如此简单。我读过很多解释,但从未真正理解链式法则的概念及其在梯度下降中的用途。
第一次看到如此精彩的解释。现在我不需要再读下去了。所有内容都解释得很清楚,特别是那张描述链式法则的精彩图片……非常感谢……
谢谢你。很高兴你喜欢。
请提供链式法则的数学示例,一步一步来
感谢您的建议。您能详细说明您想看哪一部分吗?
这对我理解链式法则是一个完美的解释。太棒了!
感谢您的反馈,Felix!
这些教程中解释的数学如此清晰优雅!
感谢您的反馈,Sofiane!
我认为他指的是“广义链式法则”部分,其中没有多变量函数的示例,无法看出这种方法在实际情况下是如何工作的。如果有一个示例会非常方便。
嗨,Sofiane……您可能会对以下内容感兴趣:
https://math.hmc.edu/calculus/hmc-mathematics-calculus-online-tutorials/multivariable-calculus/multi-variable-chain-rule/#:~:text=Multivariable%20Chain%20Rules%20allow%20us,ydydt.
如果我们简化这两个方程,LHS != RHS,
即对于 x1:LHS = del h/ del x1,
另一方面:RHS = 2(del h/ del x1)
如果我们简化这两个方程,LHS != RHS,
即对于 x1:LHS = del h/ del x1,
另一方面:RHS = 2(del h/ del x1)
尽管这看起来合乎逻辑,但您能对此有所启发吗?
谢谢
嗨,Bhavyaa……您的疑问不清楚。也许您可以指定一个实际函数,以便我们应用这些技术。
你好,先生,
我有一个疑问,当反向传播发生时,它会相对于权重求偏导数对吗!而不是输入值 xi。您能帮我澄清一下吗?
嗨,Sasi……理解反向传播可能具有挑战性,但有很多资源可以帮助您掌握这个概念,从入门材料到深入解释。以下是一些推荐的资源:
### 书籍
1. **Michael Nielsen 著《神经网络与深度学习》**
– 这本在线书籍对神经网络和反向传播提供了极好的介绍。它写得很好,并包含互动元素。
– [神经网络与深度学习](http://neuralnetworksanddeeplearning.com/)
2. **Ian Goodfellow, Yoshua Bengio, Aaron Courville 著《深度学习》**
– 一本全面涵盖深度学习各个方面的书籍,包括反向传播。适合那些希望深入理解的人。
– [深度学习书籍](https://www.deeplearningbook.org/)
3. **Christopher M. Bishop 著《模式识别与机器学习》**
– 这本书为机器学习奠定了坚实的基础,并详细解释了神经网络和反向传播。
– [模式识别与机器学习](https://www.springer.com/gp/book/9780387310732)
### 在线课程
1. **Coursera:Andrew Ng 主讲《神经网络与深度学习》**
– 作为 Coursera 深度学习专项课程的一部分,本课程对神经网络和反向传播提供了清晰简洁的介绍。
– [Coursera 神经网络与深度学习](https://www.coursera.org/learn/neural-networks-deep-learning)
2. **Udacity:《深度学习纳米学位》**
– 这个纳米学位课程包含大量关于神经网络和反向传播的内容,并附有实践项目以巩固学习。
– [Udacity 深度学习纳米学位](https://www.udacity.com/course/deep-learning-nanodegree–nd101)
3. **edX:IBM 主讲《使用 Python 和 PyTorch 进行深度学习》**
– 本课程涵盖深度学习的基础知识,包括反向传播,并提供使用 PyTorch 的实际示例。
– [edX 使用 Python 和 PyTorch 进行深度学习](https://www.edx.org/course/deep-learning-with-python-and-pytorch)
### 视频教程
1. **3Blue1Brown:《神经网络》系列**
– 这个 YouTube 系列对神经网络和反向传播提供了直观的视觉解释。强烈推荐给初学者。
– [3Blue1Brown 神经网络](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDOQy_NGj2xdtonG8zfYBa8G)
2. **Josh Starmer 的 StatQuest**
– Josh Starmer 的视频将复杂的主题分解为易于理解的片段。他关于反向传播的视频特别有帮助。
– [StatQuest: 反向传播](https://www.youtube.com/watch?v=Ilg3gGewQ5U)
### 教程和文章
1. **斯坦福大学 CS231n:用于视觉识别的卷积神经网络**
– 本课程包含关于神经网络和反向传播的详细讲义,以及实际作业。
– [CS231n 讲义](http://cs231n.github.io/)
2. **机器学习精要:《反向传播的温和介绍》**
– 一篇易于理解的文章,逐步介绍反向传播。
– [机器学习精要](https://machinelearning.org.cn/gentle-introduction-backpropagation/)
3. **走向数据科学:《反向传播揭秘》**
– 一篇以清晰解释和视觉辅助分解反向传播算法的文章。
– [走向数据科学](https://towardsdatascience.com/backpropagation-demystified-6c2edc9f0d56)
### 实践与实现
1. **Kaggle**
– 参与 Kaggle 竞赛,处理数据集,练习实现神经网络和反向传播。
– [Kaggle](https://www.kaggle.com/)
2. **GitHub 仓库**
– 探索包含各种编程语言实现的神经网络和反向传播的仓库。
– 示例:[神经网络和深度学习示例](https://github.com/rasbt/deeplearning-models)
通过探索这些资源,您将对反向传播及其如何有效训练神经网络有扎实的理解。