偏导数和梯度向量简明入门

在机器学习算法中，偏导数和梯度向量经常被用来寻找函数的最小值或最大值。梯度向量被用于神经网络、逻辑回归以及许多其他分类和回归问题的训练中。

在本教程中，您将了解偏导数和梯度向量。

完成本教程后，您将了解：

• 多变量函数
• 二元函数的水平集、等高线和图形
• 多变量函数的偏导数
• 梯度向量及其含义

让我们开始吧。

偏导数和梯度向量简明入门。照片由 Atif Gulzar 拍摄，保留部分权利。

教程概述

本教程分为三个部分；它们是：

1. 多变量函数
   1. 水平集
   2. 等高线
   3. 图形
2. 偏导数的定义
3. 梯度向量
   1. 梯度向量代表什么

多变量函数

您可以在这篇教程中回顾函数和多变量函数的概念。这里我们将提供更多关于多变量函数的细节。

多变量函数具有以下属性

• 其定义域是由 n 元组 (x_1, x_2, x_3, …, x_n) 组成的集合
• 其值域是实数集

例如，下面是一个二元函数 (n=2)

f_1(x,y) = x + y

在上述函数中，x 和 y 是自变量。它们的和决定了函数的值。该函数的定义域是 XY 笛卡尔平面上所有点的集合。要绘制这个函数的图形，需要在三维空间中进行，其中两个轴用于输入点 (x,y)，第三个轴表示 f 的值。

这是另一个二元函数的例子。f_2(x,y) = x*x + y*y

为了简化问题，我们将以二元函数为例。当然，在机器学习中，您会遇到包含数百个变量的函数。与二元函数相关的概念可以推广到这些情况。

二元函数的水平集和图形

在平面上，使函数 f(x,y) 具有恒定值（即 f(x,y)=c）的点集，称为 f 的水平集或水平曲线。

例如，对于函数 f_1，所有满足以下方程的 (x,y) 点定义了 f_1 的一个水平集

x + y = 1

我们可以看到这个水平集包含无限个点，例如 (0,2)、(1,1)、(2, 0) 等。这个水平集在 XY 平面上定义了一条直线。

总的来说，f_1 的所有水平集都定义了形如下式的直线（c 是任意实数常量）

x + y = c

同样，对于函数 f_2，一个水平集的例子是

x*x + y*y = 1

我们可以看到，任何位于以 (0,0) 为中心、半径为 1 的圆上的点都满足上述表达式。因此，这个水平集由所有位于该圆上的点组成。同样，f_2 的任何水平集都满足以下表达式（c 是任意大于等于 0 的实数常量）

x*x + y*y = c

因此，f_2 的所有水平集都是以 (0,0) 为中心的圆，每个水平集都有自己的半径。

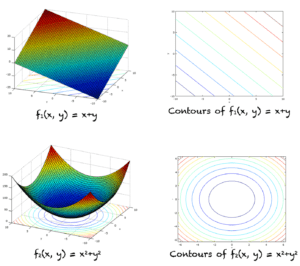
函数 f(x,y) 的图形是所有点 (x,y,f(x,y)) 的集合。它也被称为曲面 z=f(x,y)。f_1 和 f_2 的图形如下所示（左侧）。

函数 f_1 和 f_2 及其对应的等高线

二元函数的等高线

假设我们有一个二元函数 f(x,y)。如果我们用一个平面 z=c 来切割曲面 z=f(x,y)，那么我们得到所有满足 f(x,y) = c 的点集。等高线是在平面 z=c 上满足 f(x,y)=c 的点集。这与水平集略有不同，水平曲线是直接在 XY 平面上定义的。然而，许多书籍将等高线和水平曲线视为同一概念。

上图中显示了 f_1 和 f_2 的等高线（右侧）。

偏导数和梯度

函数 f 关于变量 x 的偏导数用 ∂f/∂x 表示。其表达式可以通过对 f 关于 x 求导来确定。例如，对于函数 f_1 和 f_2，我们有

∂f_1/∂x = 1

∂f_2/∂x = 2x

∂f_1/∂x 表示 f_1 相对于 x 的变化率。对于任何函数 f(x,y)，∂f/∂x 表示 f 相对于变量 x 的变化率。

∂f/∂y 的情况类似。它表示 f 相对于 y 的变化率。您可以在这篇教程中查看偏导数的正式定义。

当我们求出关于所有自变量的偏导数时，我们最终会得到一个向量。这个向量被称为 f 的梯度向量，记为 ∇f(x,y)。f_1 和 f_2 梯度的一般表达式如下（这里 i,j 是平行于坐标轴的单位向量）

∇f_1(x,y) = ∂f_1/∂xi + ∂f_1/∂yj = i+j

∇f_2(x,y) = ∂f_2/∂xi + ∂f_2/∂yj = 2xi + 2yj

从梯度的一般表达式中，我们可以计算出空间中不同点的梯度。在 f_1 的情况下，梯度向量是一个常数，即：

i+j

无论我们在三维空间中的哪个位置，梯度向量的方向和大小都保持不变。

对于函数 f_2，∇f_2(x,y) 随 (x,y) 值的变化而变化。例如，在 (1,1) 和 (2,1) 点，f_2 的梯度由以下向量给出

∇f_2(1,1) = 2i + 2j

∇f_2(2,1) = 4i + 2j

某一点的梯度向量表示什么？

多变量函数在任意点的梯度向量表示了该点变化率最大的方向。

我们可以将梯度向量与切线联系起来。如果我们站在空间中的某一点，并制定一个规则，让我们沿着该点等高线的切线行走。这意味着无论我们在哪里，我们都找到该点等高线的切线并沿着它走。如果我们遵循这个规则，我们最终会沿着 f 的等高线行走。函数的值永远不会改变，因为函数在 f 的等高线上是恒定的。

另一方面，梯度向量与切线垂直，并指向增长率最大的方向。如果我们沿着梯度的方向行走，我们将开始遇到下一个点，该点的函数值将比前一个点大。

梯度的正方向表示增长率最大的方向，而负方向表示下降率最大的方向。下图显示了函数 f_2 等高线上不同点的梯度向量的正方向。正梯度的方向由红色箭头指示。等高线的切线以绿色显示。

等高线和梯度向量的方向

为什么梯度向量在机器学习中很重要？

梯度向量在机器学习算法中非常重要且被频繁使用。在分类和回归问题中，我们通常定义均方误差函数。沿着这个函数的梯度负方向，将引导我们找到该函数具有最小值的点。

对于那些最大化它们可以达到最高准确率的函数，情况也是类似的。在这种情况下，我们将沿着该函数增长率最大的方向，即梯度向量的正方向前进。

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

• 梯度下降/梯度上升
• 海森矩阵
• 雅可比矩阵

如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

教程

• 导数
• 斜率和切线
• 多元微积分
• 用于机器学习的梯度下降
• 机器学习中的梯度是什么

资源

• 关于机器学习微积分书籍的额外资源

书籍

• 《托马斯微积分》，第14版，2017年。（基于 George B. Thomas 的原创作品，由 Joel Hass, Christopher Heil, Maurice Weir修订）
• 《微积分》，第3版，2017年。（Gilbert Strang）
• 《微积分》，第8版，2015年。（James Stewart）

总结

在本教程中，您了解了什么是多变量函数、偏导数和梯度向量。具体来说，您学到了

• 多变量函数
  • 多变量函数的等高线
  • 多变量函数的水平集
• 多变量函数的偏导数
• 梯度向量及其含义

你有什么问题吗？

在下面的评论中提出你的问题，我会尽力回答。

掌握机器学习微积分！

通过微积分概念变得更聪明

...通过更好地理解微积分的符号和术语

在我的新电子书中探索如何实现
机器学习微积分

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
微分、梯度、拉格朗日乘子法、雅可比矩阵等等...

将恰到好处的微积分知识带到
您的机器学习项目

查看内容