直线的斜率及其与曲线切线的关系是微积分中的一个基本概念。它对于理解函数导数非常重要。
在本教程中，您将了解什么是直线的斜率以及什么是曲线的切线。
完成本教程后，您将了解：
- 直线的斜率
- f(x) 在区间上相对于 x 的平均变化率
- 曲线的斜率
- 曲线上某一点的切线
让我们开始吧。
斜率与切线简介 艺术家：Jonathan Borofsky，摄影：Mehreen Saeed，保留部分权利。
教程概述
本教程分为两部分；它们是
- 直线和曲线的斜率
- 曲线的切线
直线的斜率
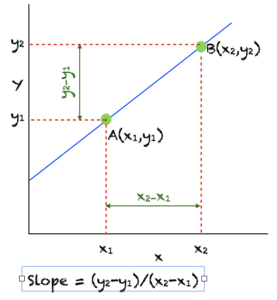
我们先回顾一下直线的斜率。在微积分中，直线的斜率定义了它的陡峭程度为一个数字。这个数字是通过将线上从一个点移动到另一个点时垂直方向的变化量除以水平方向的变化量来计算的。该图显示了如何从线上两个不同的点 A 和 B 计算斜率。
根据线上两点计算的直线斜率
一条直线可以通过线上的两个点唯一确定。直线的斜率在直线上处处相同；因此，任何一条直线也可以通过斜率和线上的一点唯一确定。从已知点，我们可以根据由直线的斜率定义的比率移动到线上的任何其他点。
曲线的平均变化率
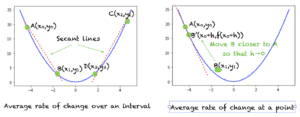
我们可以将直线斜率的思想扩展到曲线斜率。考虑下图的左图。如果我们要测量这条曲线的“陡峭程度”，它在曲线上的不同点会发生变化。从点 A 移动到点 B 时的平均变化率为负，因为当 x 增加时，函数值减小。从点 B 移动到点 A 时也是如此。因此，我们可以将其定义在区间 [x0,x1] 上为
(y1-y0)/(x1-x0)
我们可以看到，上述也是包含点 A 和 B 的割线斜率的表达式。为了刷新您的记忆，割线与曲线相交于两点。
同样，点 C 和点 D 之间的平均变化率为正，它由包含这两个点的割线斜率给出。
曲线上区间上的变化率与某一点的变化率
定义曲线的斜率
现在我们来看上图的右图。当我们将点 B 移向点 A 时会发生什么？我们称新点为 B'。当点 B' 与 A 无限接近时，割线将变成一条只接触曲线一次的线。这里 B' 的 x 坐标是 (x0+h)，其中 h 是一个无限小的值。点 B' 对应的 y 坐标值是该函数在 (x0+h) 处的值，即 f(x0+h)。
区间 [x0,x0+h] 上的平均变化率表示长度为 h 的非常小区间上的变化率，其中 h 趋近于零。这称为曲线在点 x0 处的斜率。因此，在任何点 A(x0,f(x0))，曲线的斜率定义为
曲线在点 A 处斜率的表达式等同于 f(x) 在点 x0 处的导数。因此，我们可以使用导数来求曲线的斜率。您可以在本教程中回顾导数的概念。
曲线斜率的例子
以下是曲线斜率的几个例子。
- f(x) = 1/x 在任意点 k (k≠0) 的斜率由 (-1/k^2) 给出。例如
- f(x) = 1/x 在 (x=2) 处的斜率为 -1/4
- f(x) = 1/x 在 (x=-1) 处的斜率为 -1
- f(x) = x^2 在任意点 k 处的斜率由 (2k) 给出。例如
- f(x) = x^2 在 (x=0) 处的斜率为 0
- f(x) = x^2 在 (x=1) 处的斜率为 2
- f(x) = 2x+1 的斜率是一个常数，等于 2。我们可以看到 f(x) 定义了一条直线。
- f(x) = k (其中 k 为常数) 的斜率为零，因为函数在任何地方都没有变化。因此，它在任何一点的平均变化率都为零。
切线
前面提到，任何一条直线都可以通过其斜率和通过它的一点唯一确定。我们刚刚也定义了曲线 f(x) 在点 A 处的斜率。利用这两个事实，我们将曲线 f(x) 在点 A(x0,f(x0)) 处的切线定义为满足以下两个条件的直线
- 该线通过 A 点
- 该线的斜率等于曲线在点 A 处的斜率
利用上述两个事实，我们可以很容易地确定在点 (x0,f(x0)) 处的切线方程。下面给出几个例子。
切线示例
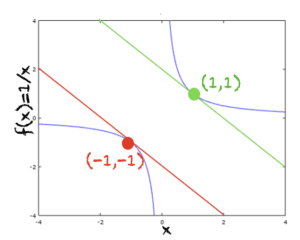
1. f(x) = 1/x
图中显示了 f(x) 的图形以及在 x=1 和 x=-1 处的切线。下面是确定 x=1 处切线的步骤。
f(x) = 1/x
- 斜率为 m，y 截距为 c 的直线方程为：y=mx+c
- 任意点处的直线斜率由函数 f'(x) = -1/x^2 给出
- 曲线在 x=1 处的切线斜率为 -1，我们得到 y=-x+c
- 切线通过点 (1,1)，因此代入上述方程得到
- 1 = -(1)+c ⟹ c = 2
- 切线的最终方程为 y = -x+2
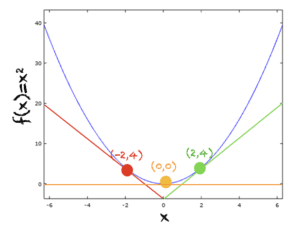
2. f(x) = x^2
下面显示了曲线以及在点 x=2、x=-2、x=0 处的切线。在 x=0 处，切线与 x 轴平行，因为 f(x) 在 x=0 处的斜率为零。
我们这样计算 x=2 处的切线方程
f(x) = x^2
- 斜率为 m，y 截距为 c 的直线方程为：y=mx+c
- 任意点处的直线斜率由函数 f'(x) = 2x 给出
- 曲线在 x=2 处的切线斜率为 4，我们得到 y=4x+c
- 切线通过点 (2,4)，因此代入上述方程得到
- 4 = 4(2)+c ⟹ c = -4
- 切线的最终方程为 y = 4x-4
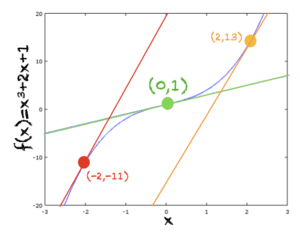
3. f(x) = x^3+2x+1
该函数如下所示，以及它在 x=0、x=2 和 x=-2 处的切线。下面是推导 x=0 处切线方程的步骤。
f(x) = x^3+2x+1
- 斜率为 m，y 截距为 c 的直线方程为：y=mx+c
- 任意点处的直线斜率由函数 f'(x) = 3x^2+2 给出
- 曲线在 x=0 处的切线斜率为 2，我们得到 y=2x+c
- 切线通过点 (0,1)，因此代入上述方程得到
- 1 = 2(0)+c ⟹ c = 1
- 切线的最终方程为 y = 2x+1
请注意，曲线在 x=2 和 x=-2 处的斜率相同，因此在 x=2 和 x=-2 处的两条切线是平行的。对于任何 x=k 和 x=-k 也是如此，因为 f'(x) = f'(-x) = 3x^2+2
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 速度与加速度
- 函数积分
如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。
进一步阅读
如果您想深入了解，本节提供了更多关于该主题的资源。
教程
资源
- 机器学习微积分书籍 的其他资源
书籍
- 《托马斯微积分》，第14版，2017年。（基于 George B. Thomas 的原创作品，由 Joel Hass, Christopher Heil, Maurice Weir修订）
- 微积分，第 3 版，2017 年。(Gilbert Strang)
- 《微积分》，第8版，2015年。（James Stewart）
总结
在本教程中，您学习了曲线在某一点的斜率和曲线在某一点的切线概念。
具体来说，你学到了：
- 什么是直线的斜率
- 曲线在区间上相对于 x 的平均变化率是多少
- 曲线在某一点的斜率
- 曲线在某一点的切线
你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。
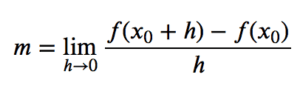
亲爱的 Mehreen 博士和 Jason 博士，
“让我们开始吧”，Jason 博士的标志性短语在乌尔都语中的对应词是“چلو شروع کریں”（使用 Google 翻译），重新翻译为“让我们开始”。
谢谢你，
悉尼的Anthony