函数极限的概念可以追溯到欧多克索斯和阿基米德等希腊学者。虽然他们从未正式定义极限,但他们的许多计算都基于这一概念。艾萨克·牛顿正式定义了极限的概念,柯西完善了这一思想。极限构成了微积分的基础,而微积分又定义了许多机器学习算法的基础。因此,理解如何评估不同类型函数的极限至关重要。
在本教程中,您将学习如何评估不同类型函数的极限。
完成本教程后,您将了解:
- 评估极限的不同规则
- 如何评估多项式和有理函数的极限
- 如何评估具有不连续点的函数的极限
- 夹逼定理
让我们开始吧。
教程概述
本教程分为3个部分;它们是
- 极限规则
- 使用极限规则评估极限的示例
- 多项式的极限
- 有理表达式的极限
- 具有不连续点的函数的极限
- 夹逼定理
极限规则
如果我们知道一些简单的原则,评估极限就很容易,这些原则如下所列。所有这些规则都基于当 x 趋近于点 k 时,两个函数 f(x) 和 g(x) 的已知极限。
使用规则评估极限的示例
以下是一些使用基本规则评估极限的示例。请注意,这些规则适用于当 x 趋近于某一点时,在该点上定义的函数。
多项式的极限
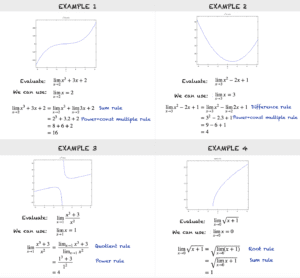
示例 1 和 2 均为多项式。从极限规则中可以看出,对于任何多项式,当 x 趋近于点 k 时,多项式的极限等于该多项式在 k 处的值。可以写为: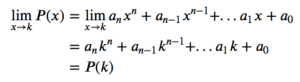
因此,我们可以通过直接代入来评估多项式的极限,例如:
lim(x→1) x^4+3x^3+2 = 1^4+3(1)^3+2 = 6
有理函数的极限
对于涉及分数的有理函数,有两种情况。一种情况是当 x 趋近于某一点且函数在该点有定义时评估极限。另一种情况是当 x 趋近于某一点且函数在该点没有定义时计算极限。
情况 1:函数有定义
与多项式的情况类似,当我们有一个函数,它是 f(x)/g(x) 形式的有理表达式,并且在某一点分母不为零时,则:
lim(x→k) f(x)/g(x) = f(k)/g(k) 如果 g(k)≠0
因此,我们可以通过直接代入来评估这个极限。例如:
lim(x→0)(x^2+1)/(x-1) = -1
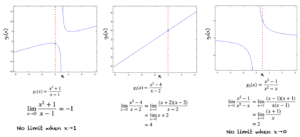
在这里,我们可以应用商规则,或者更简单地,代入 x=0 来评估极限。然而,当 x 趋近于 1 时,这个函数没有极限。请看下图中的第一个图。
情况 2:函数未定义
我们来看另一个例子
lim(x→2)(x^2-4)/(x-2)
在 x=2 处,我们遇到了一个问题。分母为零,因此函数在 x=2 处未定义。从图中可以看出,该函数和 (x+2) 的图是相同的,除了在 x=2 处有一个“空心点”。在这种情况下,我们可以消去公因子,然后仍然可以评估 (x→2) 的极限,如下所示:
lim(x→2)(x^2-4)/(x-2) = lim(x→2)(x-2)(x+2)/(x-2) = lim(x→2)(x+2) = 4
下图展示了上面两个例子以及第三个类似的 g_3(x) 例子
具有不连续点的函数的情况
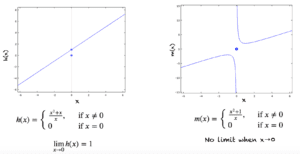
假设我们有一个函数 h(x),它对所有实数都有定义
h(x) = (x^2+x)/x, 如果 x≠0
h(x) = 0, 如果 x=0
函数 g(x) 在 x=0 处有一个不连续点,如下图所示。当计算 lim(x→0)h(x) 时,我们必须观察当 x 接近 0 时(而不是当 x=0 时)h(x) 的变化。当我们从两侧接近 x=0 时,h(x) 接近 1,因此 lim(x→0)h(x)=1。
下图中的函数 m(x) 是另一个有趣的例子。这个函数也对所有实数都有定义,但是当 x→0 时,极限不存在。
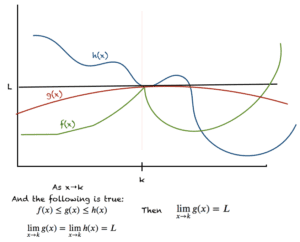
夹逼定理
这个定理也称为夹逼定理或两边夹定理。它指出,当以下条件为真时:
- x 接近 k
- f(x) <= g(x) <= h(x)
- lim(x→k)f(x) = lim(x→k)h(x) = L
那么当 x 趋近于 k 时,g(x) 的极限为
lim(x→k)g(x) = L
这个定理如下图所示
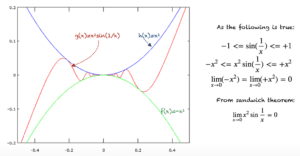
利用这个定理,我们可以评估许多复杂函数的极限。一个著名的例子涉及正弦函数
lim(x→0)x^2sin(1/x)
我们知道 sin(x) 总是介于 -1 和 +1 之间。利用这个事实,我们可以如下所示解出这个极限
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 洛必达法则和不定形式(需要函数导数)
- 用函数极限定义的函数导数
- 函数积分
如果您探索了这些扩展内容中的任何一个,我很想知道。请在下面的评论中发布您的发现。
进一步阅读
学习和理解数学的最佳方法是通过练习和解决更多问题。如果您想深入了解此主题,本节提供了更多资源。
教程
书籍
- 托马斯微积分,第 14 版,2017 年。(基于 George B. Thomas 的原创作品,由 Joel Hass、Christopher Heil、Maurice Weir 修订)
- 《微积分》,第3版,2017年。(Gilbert Strang)
- 微积分,第 8 版,2015 年。(James Stewart)
总结
在本教程中,您学习了如何评估不同类型函数的极限。
具体来说,你学到了:
- 评估不同函数极限的规则。
- 评估多项式和有理函数的极限
- 评估函数存在不连续点时的极限
您有任何问题吗?请在下面的评论中提问,我将尽力回答。祝您学习微积分愉快!

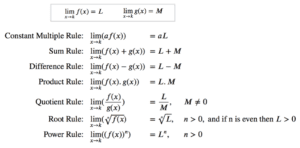







感谢您的清晰解释!
很高兴它有帮助。
这太棒了!
真是一篇很酷的文章…现在让我把它翻译成 Python!
好主意!
感谢您在这里提供的清晰解释
不客气。
这让我想起了数学……谢谢你。