函数导数简明入门

导数是微积分中许多主题的基石。理解积分、梯度、海森矩阵等等，它都至关重要。

在本教程中，您将了解导数的定义、表示法以及如何基于该定义计算导数。您还将了解为什么函数导数本身也是一个函数。

完成本教程后，您将了解：

• 函数导数的定义
• 如何根据定义计算函数导数
• 为什么某些函数在某一点没有导数

让我们开始吧。

函数导数的温和介绍 图片由 Mehreen Saeed 提供，保留部分权利

教程概述

本教程分为三个部分；它们是：

1. 用于函数导数的定义和表示法
2. 如何使用定义计算函数导数
3. 为什么某些函数在某一点没有导数

什么是函数导数

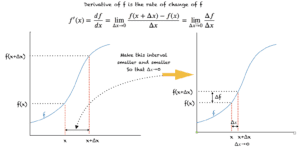
简单来说，函数 f(x) 的导数代表其变化率，并用 f'(x) 或 df/dx 表示。我们先来看它的定义和导数的图示说明。

函数导数定义的图示

图中，Δx 表示 x 的值变化。我们不断缩小 x 和 (x+Δx) 之间的区间，直到它变得无穷小。因此，我们有极限 (Δ????→0)。分子 f(x+Δx)-f(x) 表示函数 f 在区间 Δx 上的对应变化。这使得函数 f 在点 x 的导数成为 f 在该点的变化率。

需要注意的重要一点是，Δx，即 x 的变化可以是负的或正的。因此

0<|Δx|< ????，

其中 ???? 是一个无穷小的数值。

关于表示法

函数导数可以用 f'(x) 和 df/dx 来表示。数学巨匠牛顿使用 f'(x) 来表示函数导数。另一位数学英雄莱布尼茨则使用 df/dx。因此 df/dx 是一个整体，不应被误认为是分数。它读作“f 关于 x 的导数”，也表明 x 是自变量。

与速度的联系

导数最常被引用的例子之一就是速度。速度是距离相对于时间的变化率。因此，如果 f(t) 表示在时间 t 处的行进距离，那么 f'(t) 就是在时间 t 处的速度。接下来的部分将展示各种计算导数的例子。

微分示例

求函数导数的方法称为微分。在本节中，我们将学习如何使用导数定义来求不同函数的导数。稍后，一旦您对定义更加熟悉，就可以使用已定义的规则来微分函数。

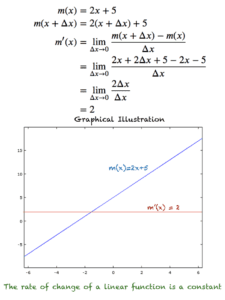
示例 1：m(x) = 2x+5

我们从一个简单的线性函数 m(x) = 2x+5 的例子开始。我们可以看到 m(x) 以恒定的速率变化。我们可以按如下方式对该函数进行微分。

m(x) = 2x+5 的导数

上图显示了函数 m(x) 的变化方式，并且还表明无论我们选择哪个 x 值，m(x) 的变化率始终保持为 2。

示例 2：g(x) = x^2

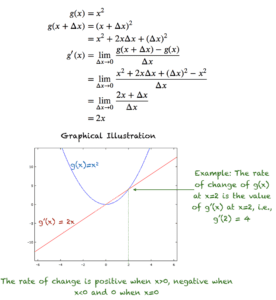
假设我们有函数 g(x) = x^2。下图显示了 g(x) 相对于 x 的导数是如何计算的。图中还有一个函数及其导数的图。

g(x) = x^2 的导数

由于 g'(x) = 2x，因此 g'(0) = 0，g'(1) = 2，g'(2) = 4 且 g'(-1) = -2，g'(-2) = -4

从图中可以看出，对于很大的负 x 值，g(x) 的值非常大。当 x < 0 时，x 增加会减小 g(x)，因此 x<0 时 g'(x) < 0。图形在 x=0 处变平，此时 g(x) 的导数或变化率变为零。当 x>0 时，g(x) 随着 x 的增加呈二次方增长，因此导数也为正。

示例 3：h(x) = 1/x

假设我们有函数 h(x) = 1/x。下图显示了 h(x) 相对于 x 的微分（对于 x ≠0）以及说明导数的图。蓝色曲线表示 h(x)，红色曲线表示其对应的导数。

h(x) = 1/x 的导数

可微性与连续性

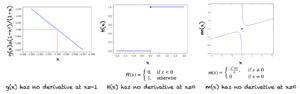
对于示例 3，函数 h(x) = 1/x 在点 x=0 处是未定义的。因此，其导数 (-1/x^2) 在 x=0 处也是未定义的。如果一个函数在某点不连续，则在该点就没有导数。以下是一些函数不可微的场景。

1. 如果函数在该点未定义
2. 函数在该点没有极限
3. 如果函数在该点不连续
4. 函数在该点有跳跃

以下是一些例子

没有导数的点的示例

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

• 速度与瞬时变化率
• 导数规则
• 积分

如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

教程

• 极限与连续性
• 评估极限

资源

• 关于机器学习微积分书籍的额外资源

书籍

• 《托马斯微积分》，第14版，2017年。（基于 George B. Thomas 的原创作品，由 Joel Hass, Christopher Heil, Maurice Weir修订）
• 微积分，第三版，2017 年。(Gilbert Strang)
• 《微积分》，第8版，2015年。（James Stewart）

总结

在本教程中，您了解了函数导数和函数微分的基础知识。

具体来说，你学到了：

• 函数导数的定义和表示法
• 如何使用定义微分函数
• 函数何时不可微

您有任何问题吗？请在下方的评论区提问，我会尽力回答。

掌握机器学习微积分！

通过微积分概念变得更聪明

...通过更好地理解微积分的符号和术语

在我的新电子书中探索如何实现
机器学习微积分

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
微分、梯度、拉格朗日乘子法、雅可比矩阵等等...

将恰到好处的微积分知识带到
您的机器学习项目

查看内容