近似法简明入门

在诸如分类或回归等机器学习任务中，近似技术在从数据中学习方面发挥着关键作用。许多机器学习方法通过学习算法来近似输入和输出之间的函数或映射。

在本教程中，您将了解什么是近似及其在机器学习和模式识别中的重要性。

完成本教程后，您将了解：

•  什么是近似
• 近似在机器学习中的重要性

让我们开始吧。

近似介绍。图片由 M Mani 提供，保留部分权利。

教程概述

本教程分为3个部分；它们是

1. 什么是近似？
2. 当函数形式未知时的近似
3. 当函数形式已知时的近似

什么是近似？

我们经常遇到近似。例如，无理数 π 可以近似为 3.14。更精确的值是 3.141593，它仍然是一个近似值。您可以类似地近似所有无理数（如 sqrt(3)、sqrt(7) 等）的值。

当数值、模型、结构或函数未知或难以计算时，都会使用近似。在本文中，我们将重点关注函数近似并描述其在机器学习问题中的应用。有两种不同的情况：

1. 函数已知，但计算其精确值困难或计算成本高。在这种情况下，使用近似方法来找到接近函数实际值的值。
2. 函数本身未知，因此使用模型或学习算法来紧密地找到一个能够产生接近未知函数输出的输出的函数。

函数形式已知时的近似

如果函数形式已知，那么微积分和数学中一种众所周知的方法是通过泰勒级数进行近似。函数的泰勒级数是无限项的总和，这些项是使用函数的导数计算的。本教程中讨论了函数的泰勒级数展开。

微积分和数学中另一种众所周知的近似方法是牛顿法。它可用于近似多项式的根，因此成为近似不同值的平方根或不同数的倒数等数量的有用技术。

函数形式未知时的近似

在数据科学和机器学习中，假设存在一个潜在函数，它掌握着输入和输出之间关系的关键。这个函数的具体形式是未知的。这里，我们讨论了几个采用近似的机器学习问题。

回归中的近似

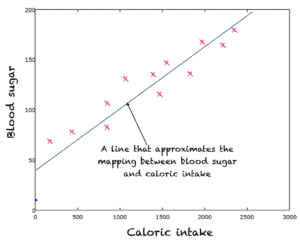
回归涉及在给定一组输入的情况下预测输出变量。在回归中，真正将输入变量映射到输出的函数是未知的。假设某个线性或非线性回归模型可以近似输入到输出的映射。 

例如，我们可能拥有与每日消耗卡路里和相应的血糖相关的数据。为了描述卡路里输入和血糖输出之间的关系，我们可以假设一个直线关系/映射函数。因此，直线是输入到输出映射的近似。使用诸如最小二乘法之类的学习方法来找到这条线。

卡路里计数与血糖之间关系的直线近似

分类中的近似

神经网络是分类问题中近似函数的模型的典型例子。假设神经网络作为一个整体可以近似一个将输入映射到类别标签的真实函数。然后使用梯度下降或其他学习算法通过调整神经网络的权重来学习该函数近似。

神经网络近似一个将输入映射到输出的潜在函数

无监督学习中的近似

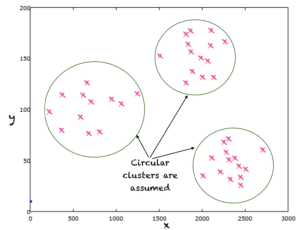
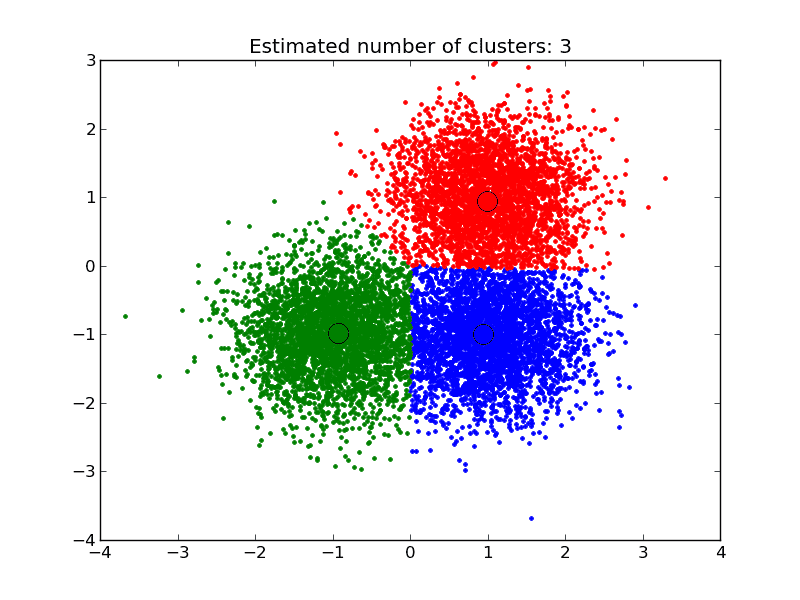
下面是无监督学习的一个典型例子。这里我们在二维空间中有一些点，这些点都没有给出标签。聚类算法通常根据模型假设一个点可以被分配到一个类别或标签。例如，k-means通过假设数据簇是圆形的来学习数据的标签，因此，将相同标签或类别分配给位于同一圆形或多维数据情况下的n维球体中的点。在下图中，我们通过圆形函数来近似点与其标签之间的关系。

聚类算法近似一个模型，该模型确定输入点的聚类或未知标签

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

• 麦克劳林级数
• 泰勒级数

如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

教程

• 神经网络是函数近似算法
• 维基百科关于近似的文章

资源

• Jason Brownlee 关于机器学习微积分书籍的优秀资源

书籍

• Christopher M. Bishop 著的《模式识别与机器学习》。
• Ian Goodfellow、Joshua Begio、Aaron Courville 著的《深度学习》。
• 托马斯微积分，第 14 版，2017 年。（基于 George B. Thomas 的原创作品，由 Joel Hass、Christopher Heil、Maurice Weir 修订）

总结

在本教程中，您了解了什么是近似。具体来说，您学习了

• 近似
• 函数形式已知时的近似
• 函数形式未知时的近似

你有什么问题吗？

请在下方评论中提出您的问题，我将尽力回答。

掌握机器学习微积分！

通过微积分概念变得更聪明

...通过更好地理解微积分的符号和术语

在我的新电子书中探索如何实现
机器学习微积分

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
微分、梯度、拉格朗日乘子法、雅可比矩阵等等...

将恰到好处的微积分知识带到
您的机器学习项目

查看内容