优化/数学规划简明介绍

无论是监督学习问题还是无监督学习问题，后台都会有一些优化算法在运行。几乎任何分类、回归或聚类问题都可以被看作是一个优化问题。

在本教程中，您将了解什么是优化以及与之相关的概念。

完成本教程后，您将了解：

• 什么是数学规划或优化
• 最大化和最小化问题之间的区别
• 局部和全局最优解之间的区别
• 约束优化和无约束优化之间的区别
• 线性规划和非线性规划之间的区别
• 优化示例

让我们开始吧。

优化入门。图片由 Mehtab Farooq 拍摄，部分权利保留。

教程概述

本教程分为两部分；它们是

1. 与优化相关的各种入门主题
   1. 约束优化与无约束优化
   2. 等式约束与不等式约束
   3. 可行域
2. 机器学习中的优化示例

什么是优化或数学规划？

在微积分和数学中，优化问题也被称为数学规划。简单来说，它是指我们找到一个最符合给定准则或约束的元素、变量或数量的机制。

最大化与最小化问题

优化问题最简单的情况是标量函数的最小化或最大化。如果有一个或多个变量的标量函数 f(x_1, x_2, … x_n)，那么以下就是一个优化问题

找到 x_1, x_2, …, x_n，使 f(x) 最小

或者我们也可以有一个等效的最大化问题。

当我们定义量化误差或惩罚的函数时，我们应用最小化问题。另一方面，如果学习算法构建一个函数来模拟方法的准确性，我们就会最大化这个函数。

许多自动化优化软件工具通常只实现最大化问题或最小化任务之一，而不是两者都实现。因此，我们可以通过在 f(x) 上添加负号，将最大化问题转换为最小化问题（反之亦然），即：

使 f(x) 相对于 x 最大化等价于 使 -f(x) 相对于 x 最小化

由于这两个问题是等价的，在本教程的其余部分，我们只讨论最小化或最大化问题。相同的规则和定义也适用于其等效形式。

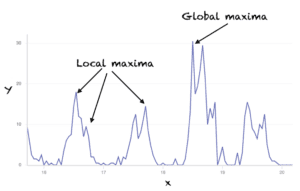
全局最优与局部最优

在机器学习中，我们经常遇到高度非线性且具有复杂“地形”的函数。函数有可能在其周围的小范围或局部区域内具有最低值。这样的点称为局部最小值点。

与全局最小值点相对，全局最小值点是指函数在其整个域内具有最低值的点。下图显示了局部最大值点和全局最大值点。

局部最大值点和全局最大值点

无约束优化与约束优化

机器学习中有很多问题，我们感兴趣的是在没有任何空间区域约束或限制的情况下找到全局最优解。这类问题称为无约束优化问题。

有时我们必须解决受某些约束条件的优化问题。这类优化问题称为约束优化问题。例如

最小化 x^2 + y^2 且 x + y <= 1

约束优化的例子有

1. 在域中变量之和必须为一的情况下，求函数的最小值
2. 在某些向量相互正交的情况下，求函数的最小值
3. 在某些域变量位于特定范围内的情况下，求函数的最小值。

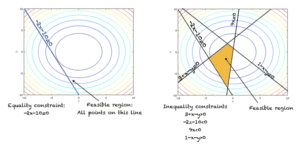
可行域

空间中所有满足问题约束条件的点构成了可行域。优化算法在可行域中寻找最优解。两种约束类型的可行域如下图下一节所示。

对于无约束优化问题，函数的整个域都是可行域。

等式约束与不等式约束

优化问题中施加的约束可以是等式约束或不等式约束。下图显示了两种类型的约束。

等式约束与不等式约束

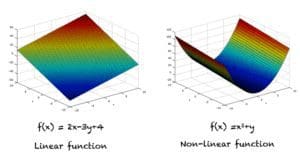
线性规划与非线性规划

如果目标函数是线性的，并且所有等式或不等式约束也是线性约束，那么这个优化问题就称为线性规划问题。

如果目标函数是非线性的，或者一个或多个约束是非线性的，那么我们就会遇到非线性规划问题。

要直观地了解线性函数和非线性函数之间的区别，请查看下图。

线性函数与非线性函数

机器学习中的优化示例

下面列出了一些采用优化的著名机器学习算法。您应该记住，几乎所有机器学习算法都采用某种优化。

1. 神经网络中的梯度下降（无约束优化）。
2. 支持向量机中的拉格朗日乘数法（约束优化）。
3. 主成分分析（约束优化）
4. 通过期望最大化算法进行聚类（约束优化）
5. 逻辑回归（无约束优化）
6. 进化学习算法中的遗传算法（存在不同的变体来解决约束优化和无约束优化问题）。

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

• 拉格朗日乘数法
• 非线性优化技术
• 单纯形法

如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

教程

• 多变量函数和梯度向量
• 用于机器学习的梯度下降
• 为什么优化在机器学习中很重要
• 如何选择优化算法

资源

• 关于机器学习微积分书籍的额外资源

书籍

• 托马斯微积分，第 14 版，2017 年。（基于 George B. Thomas 的原创作品，由 Joel Hass、Christopher Heil、Maurice Weir 修订）
• 微积分，第 3 版，2017 年。（Gilbert Strang）
• 微积分，第 8 版，2015 年。（James Stewart）

总结

在本教程中，您了解了什么是数学规划或优化问题。具体来说，您学习了

• 最大化与最小化
• 约束优化与无约束优化
• 为什么优化在机器学习中很重要

你有什么问题吗？

请在下方评论中提出您的问题，我将尽力回答。

掌握机器学习微积分！

通过微积分概念变得更聪明

...通过更好地理解微积分的符号和术语

在我的新电子书中探索如何实现
机器学习微积分

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
微分、梯度、拉格朗日乘子法、雅可比矩阵等等...

将恰到好处的微积分知识带到
您的机器学习项目

查看内容