Sigmoid 函数入门指南

无论您是自己实现神经网络，还是使用内置的神经网络学习库，理解 sigmoid 函数的意义都至关重要。Sigmoid 函数是理解神经网络如何学习复杂问题的关键。该函数还为发现其他函数奠定了基础，这些函数可以为深度学习架构中的监督学习提供高效且良好的解决方案。

在本教程中，您将了解 sigmoid 函数及其在神经网络中从示例中学习的作用。

完成本教程后，您将了解：

• Sigmoid 函数
• 线性与非线性可分性
• 为什么使用 sigmoid 单元的神经网络可以创建复杂的决策边界

让我们开始吧。

Sigmoid 函数的入门介绍。照片由 Mehreen Saeed 拍摄，保留部分权利。

教程概述

本教程分为3个部分；它们是

1. Sigmoid 函数
   1. Sigmoid 函数及其性质
2. 线性与非线性可分问题
3. 在神经网络中使用 sigmoid 作为激活函数

Sigmoid 函数

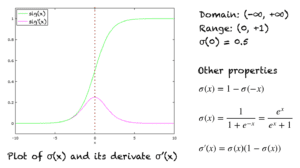
Sigmoid 函数是 logistic 函数的一种特殊形式，通常表示为 σ(x) 或 sig(x)。它由以下公式给出：

σ(x) = 1/(1+exp(-x))

Sigmoid 函数的性质和恒等式

Sigmoid 函数的图形如上图绿色线所示，是一个 S 形曲线。图中还显示了导数的图形（粉色）。导数的表达式以及一些重要性质显示在右侧。

Sigmoid 函数及其导数的图形。还显示了一些重要性质。

其他一些性质包括：

1. 定义域：(-∞, +∞)
2. 值域：(0, +1)
3. σ(0) = 0.5
4. 该函数单调递增。
5. 该函数在处处连续。
6. 该函数在其定义域内的处处可导。
7. 在数值上，计算该函数在很小的数值范围（例如 [-10, +10]）上的值就足够了。对于小于 -10 的值，函数的值几乎为零。对于大于 10 的值，函数的值几乎为一。

Sigmoid 作为压缩函数

Sigmoid 函数也称为压缩函数，因为它的定义域是所有实数的集合，而值域是 (0, 1)。因此，如果函数的输入是一个非常大的负数或非常大的正数，输出总是在 0 和 1 之间。对于 -∞ 和 +∞ 之间的任何数字也是如此。

Sigmoid 作为神经网络中的激活函数

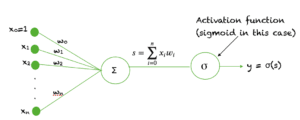
Sigmoid 函数用作神经网络中的激活函数。简单回顾一下激活函数是什么，下图显示了激活函数在神经网络一层中的作用。输入的加权和通过激活函数，该输出作为下一层的输入。

神经网络中的 sigmoid 单元

当神经元的激活函数是 sigmoid 函数时，可以保证该单元的输出总是在 0 和 1 之间。此外，由于 sigmoid 是一个非线性函数，该单元的输出将是输入加权和的非线性函数。这种采用 sigmoid 函数作为激活函数的神经元被称为 sigmoid 单元。

线性与非线性可分？

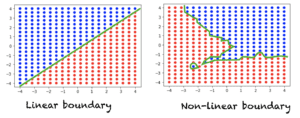
假设我们有一个典型的分类问题，其中我们有一组空间中的点，每个点都被分配一个类别标签。如果一条直线（或 n 维空间中的超平面）可以将两个类别分开，那么我们有一个线性可分问题。另一方面，如果一条直线不足以区分两个类别，那么我们有一个非线性可分问题。下图显示了二维空间中的数据。每个点都被分配一个红色或蓝色的类别标签。左图显示了一个线性可分问题，该问题需要线性边界来区分两个类别。右图显示了一个非线性可分问题，该问题需要非线性决策边界。

线性与非线性可分问题

对于三维空间，线性决策边界可以通过平面方程来描述。对于 n 维空间，线性决策边界由超平面方程描述。

为什么 Sigmoid 函数在神经网络中很重要？

如果我们在神经网络中使用线性激活函数，那么该模型只能学习线性可分的问题。然而，通过增加一个隐藏层和一个隐藏层中的 sigmoid 激活函数，神经网络可以轻松学习非线性可分的问题。使用非线性函数会产生非线性边界，因此，sigmoid 函数可以在神经网络中用于学习复杂的决策函数。

可以在神经网络中用作激活函数的唯一非线性函数是单调递增的函数。所以例如，sin(x) 或 cos(x) 不能用作激活函数。此外，激活函数应该在整个实数空间中处处有定义且连续。函数还要求在整个实数空间中可导。

通常，反向传播算法使用梯度下降来学习神经网络的权重。为了推导该算法，需要激活函数的导数。

Sigmoid 函数在处处单调、连续且可导，再加上其导数可以表示为其自身函数的性质，使得在反向传播算法中使用时，可以轻松推导出学习神经网络权重更新方程。

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

• 其他非线性激活函数，例如 tanh 函数
• ReLU（修正线性单元）简介
• 深度学习

如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

教程

• 微积分实践：神经网络
• 梯度下降过程入门
• 神经网络是函数逼近算法
• 如何为深度学习选择激活函数

资源

• Jason Brownlee 的优质资源 机器学习微积分书籍

书籍

• 模式识别与机器学习 作者：Christopher M. Bishop。
• 深度学习 作者：Ian Goodfellow, Joshua Begio, Aaron Courville。
• Thomas Calculus，第 14 版，2017 年。(基于 George B. Thomas 的原作，由 Joel Hass, Christopher Heil, Maurice Weir 修改)

总结

在本教程中，您了解了 sigmoid 函数。具体来说，您学习了：

• Sigmoid 函数及其性质
• 线性与非线性决策边界
• 为什么在隐藏层添加 sigmoid 函数可以使神经网络学习复杂的非线性边界

你有什么问题吗？

请在下方评论中提出您的问题，我将尽力回答。