梯度下降过程简明介绍

梯度下降过程在机器学习中具有至关重要的作用。它常用于分类和回归问题中最小化误差函数，也用于训练神经网络和深度学习架构。

在本教程中，您将了解梯度下降过程。

完成本教程后，您将了解：

• 梯度下降法
• 梯度下降在机器学习中的重要性

让我们开始吧。

梯度下降简介。图片由 Mehreen Saeed 提供，保留部分权利。

教程概述

本教程分为两部分；它们是

1. 梯度下降过程
2. 梯度下降过程的求解示例

先决条件

本教程假定您已具备以下主题的先决知识：

• 多变量函数
• 偏导数和梯度向量

您可以通过点击上方链接复习这些概念。

梯度下降过程

梯度下降过程是一种寻找函数最小值的算法。

假设我们有一个函数 f(x)，其中 x 是一个由多个变量组成的元组，即 x = (x_1, x_2, …x_n)。另外，假设 f(x) 的梯度由 ∇f(x) 给出。我们希望找到使函数取最小值的变量值 (x_1, x_2, …x_n)。在任何迭代 t 中，我们将元组 x 的值表示为 x[t]。因此，x[t][1] 是迭代 t 时 x_1 的值，x[t][2] 是迭代 t 时 x_2 的值，依此类推。

符号说明

我们有以下变量：

• t = 迭代次数
• T = 总迭代次数
• n = f 定义域中的总变量数（也称为 x 的维度）
• j = 变量编号的迭代器，例如，x_j 表示第 j 个变量
• ???? = 学习率
• ∇f(x[t]) = 迭代 t 时 f 的梯度向量值

训练方法

梯度下降算法的步骤如下。这也称为训练方法。

1. 选择一个随机初始点 x_initial 并设置 x[0] = x_initial
2. 对于迭代 t=1..T
   • 更新 x[t] = x[t-1] – ????∇f(x[t-1])

就是这么简单！

学习率 ???? 是梯度下降过程中用户定义的变量。其值范围在 [0,1] 之间。

上述方法表示，在每次迭代中，我们必须通过沿着梯度向量负方向迈出小步来更新 x 的值。如果 ????=0，则 x 不会发生变化。如果 ????=1，则就像沿着梯度向量负方向迈出一大步。通常，???? 设置为一个小值，如 0.05 或 0.1。它在训练过程中也可以是可变的。因此，您的算法可以从一个大值（例如 0.8）开始，然后逐渐减小到较小的值。

梯度下降示例

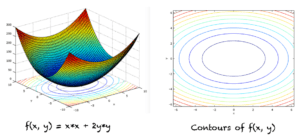
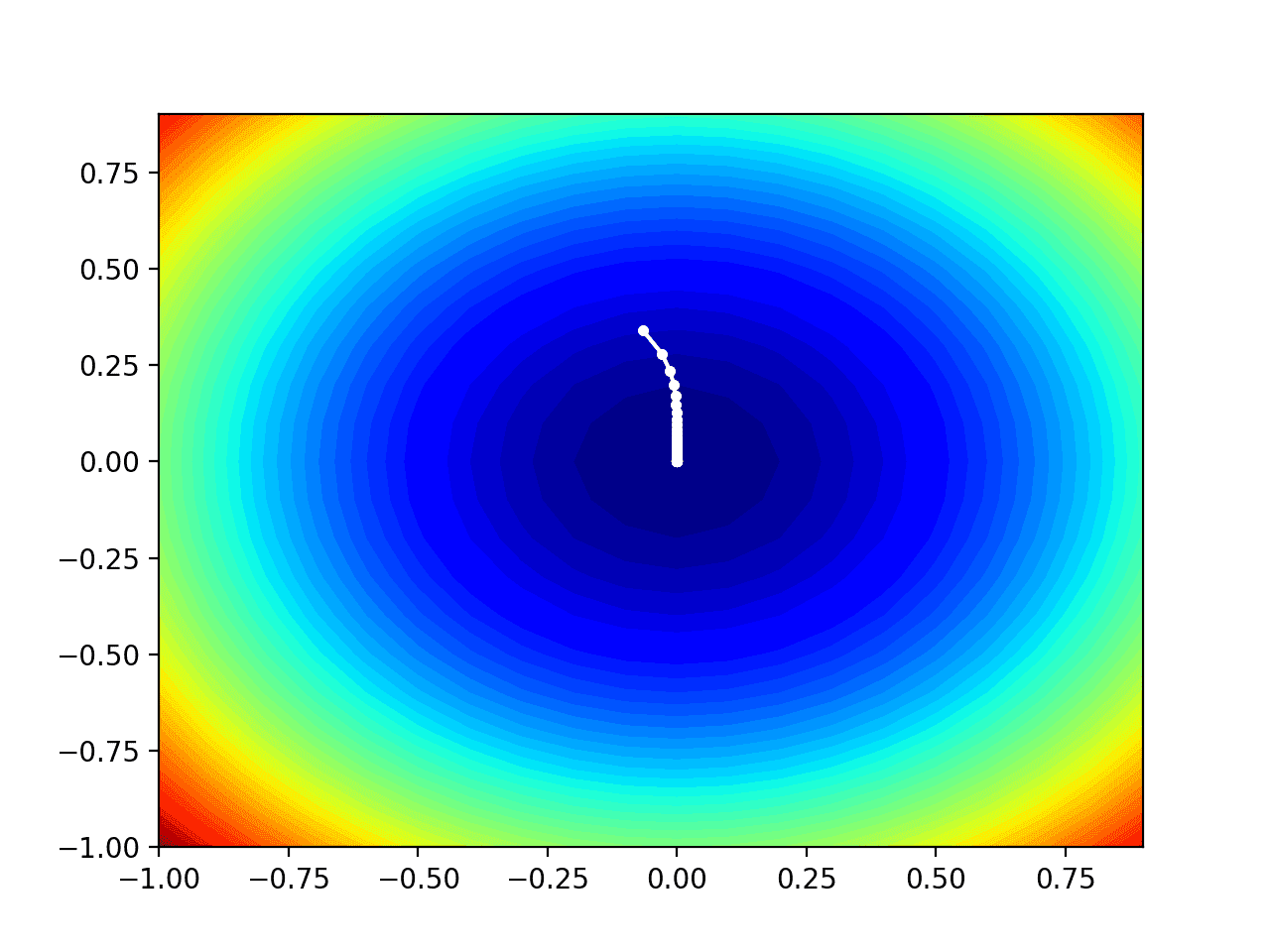
我们来求以下两个变量函数的最小值，其图和等高线如下图所示：

f(x,y) = x*x + 2y*y

f(x,y) = x*x + 2y*y 的图和等高线

梯度向量的一般形式由下式给出：

∇f(x,y) = 2xi + 4yj

算法的两次迭代，T=2 和 ????=0.1，如下所示：

1. 初始 t=0
   • x[0] = (4,3)     # 这是一个随机选择的点
2. 在 t = 1 时
   • x[1] = x[0] – ????∇f(x[0])
   • x[1] = (4,3) – 0.1*(8,12)
   • x[1] = (3.2,1.8)
3. 在 t=2 时
   • x[2] = x[1] – ????∇f(x[1])
   • x[2] = (3.2,1.8) – 0.1*(6.4,7.2)
   • x[2] = (2.56,1.08)

如果您继续运行上述迭代，该过程最终将到达函数最小值的点，即 (0,0)。

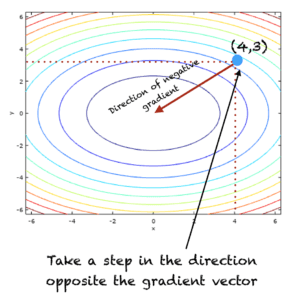
在迭代 t=1 时，算法如下图所示：

梯度下降过程示意图

运行多少次迭代？

通常，梯度下降会一直运行，直到 x 的值不再改变或 x 的变化低于某个阈值。停止准则也可以是用户定义的迭代最大次数（我们之前定义为 T）。

添加动量

梯度下降可能会遇到以下问题：

1. 在两个或更多点之间震荡
2. 陷入局部最小值
3. 过冲并错过最小值点

为了解决上述问题，可以在梯度下降算法的更新方程中添加一个动量项，如下所示：

x[t] = x[t-1] – ????∇f(x[t-1]) + ????*Δx[t-1]

其中 Δx[t-1] 表示 x 的变化，即：

Δx[t] = x[t] – x[t-1]

t=0 时的初始变化是零向量。对于这个问题，Δx[0] = (0,0)。

关于梯度上升

有一个相关的梯度上升过程，它用于寻找函数的最大值。在梯度下降中，我们沿着函数最大下降率的方向前进，这是负梯度向量的方向。而在梯度上升中，我们沿着函数最大上升率的方向前进，这是正梯度向量所指的方向。我们也可以通过在 f(x) 前面加一个负号，将最大化问题转化为最小化问题，即：

为什么梯度下降在机器学习中很重要？

梯度下降算法常用于机器学习问题中。在许多分类和回归任务中，均方误差函数用于将模型拟合到数据。梯度下降过程用于识别导致最低均方误差的最佳模型参数。

梯度上升也以类似的方式用于涉及最大化函数的问题。

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

• 海森矩阵
• 雅可比矩阵

如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

教程

• 导数
• 斜率和切线
• 用于机器学习的梯度下降
• 机器学习中的梯度是什么
• 偏导数和梯度向量

资源

• 机器学习微积分书籍 的其他资源

书籍

• 《托马斯微积分》，第14版，2017年。（基于 George B. Thomas 的原创作品，由 Joel Hass, Christopher Heil, Maurice Weir修订）
• 微积分，第3版，2017年。(Gilbert Strang)
• 《微积分》，第8版，2015年。（James Stewart）

总结

在本教程中，您了解了梯度下降算法。具体来说，您学习了

• 梯度下降过程
• 如何应用梯度下降过程来寻找函数的最小值
• 如何将最大化问题转化为最小化问题

你有什么问题吗？

在下面的评论中提出你的问题，我会尽力回答。

掌握机器学习微积分！

通过微积分概念变得更聪明

...通过更好地理解微积分的符号和术语

在我的新电子书中探索如何实现
机器学习微积分

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
微分、梯度、拉格朗日乘子法、雅可比矩阵等等...

将恰到好处的微积分知识带到
您的机器学习项目

查看内容