人工神经网络是一种计算模型,用于近似输入和输出之间的映射关系。
它的灵感来源于人脑的结构,同样由相互连接的神经元网络组成,这些神经元在接收到来自相邻神经元的一组刺激后传播信息。
训练神经网络涉及一个同时采用反向传播和梯度下降算法的过程。正如我们将看到的,这两种算法都大量使用了微积分。
在本教程中,您将了解微积分的各个方面是如何应用于神经网络的。
完成本教程后,您将了解:
- 人工神经网络由神经元层和连接组成,其中每个连接都被赋予一个权重值。
- 每个神经元都实现一个非线性函数,将一组输入映射到一个输出激活值。
- 在训练神经网络时,反向传播和梯度下降算法大量使用了微积分。
让我们开始吧。

微积分在行动:神经网络
图片由 Tomoe Steineck 拍摄,部分权利保留。
教程概述
本教程分为三个部分;它们是:
- 神经网络简介
- 神经元的数学原理
- 训练网络
先决条件
对于本教程,我们假设您已经了解以下内容:
您可以通过点击上面给出的链接来复习这些概念。
神经网络简介
人工神经网络可以被视为函数逼近算法。
在监督学习环境中,当给定许多代表感兴趣问题的输入观测值及其相应的目标输出时,人工神经网络将寻求近似两者之间存在的映射关系。
神经网络是一种受人脑结构启发的计算模型。
– 第65页, 深度学习, 2019。
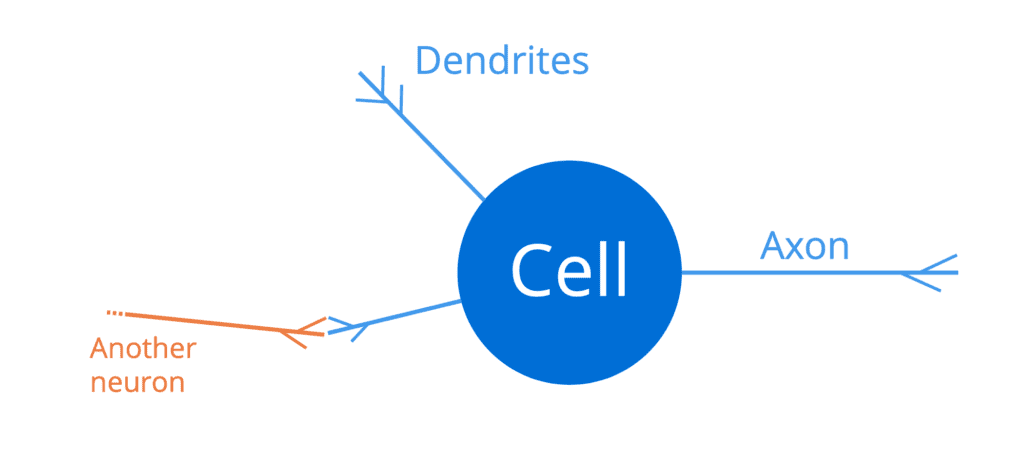
人脑由一个庞大且相互连接的神经元网络组成(大约一千亿个),每个神经元都包含一个细胞体、一组称为树突的纤维和一个轴突。
树突充当神经元的输入通道,而轴突充当输出通道。因此,神经元将通过其树突接收输入信号,这些树突又连接到其他相邻神经元的(输出)轴突。通过这种方式,足够强的电脉冲(也称为动作电位)可以沿着一个神经元的轴突传输到所有连接到它的其他神经元。这使得信号可以在人脑结构中传播。
因此,神经元就像一个全或无的开关,它接收一组输入,然后输出一个动作电位或不输出任何东西。
– 第66页, 深度学习, 2019。
人工神经网络类似于人脑的结构,因为 (1) 它同样由大量相互连接的神经元组成,(2) 旨在通过接收来自相邻神经元的一组刺激并将其映射到输出,从而将信息传播到整个网络,以馈送到下一层神经元。
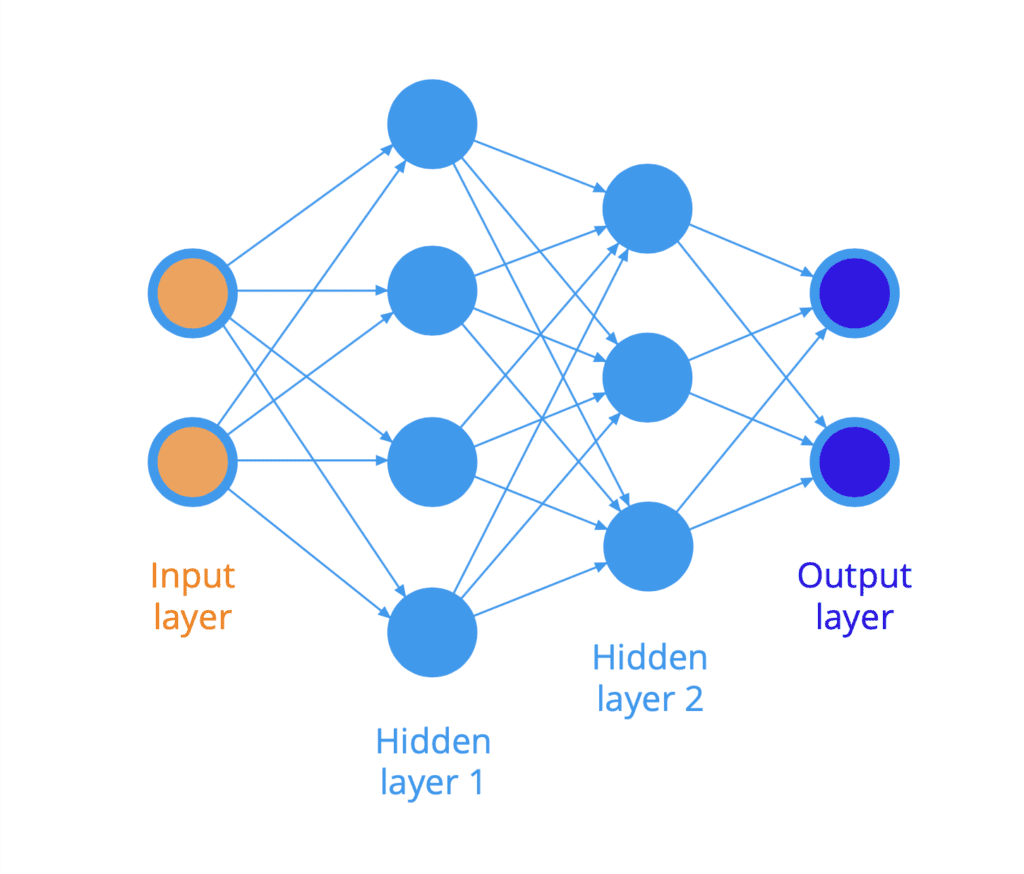
人工神经网络的结构通常组织成神经元层(回想树状图的描述)。例如,下图说明了一个全连接神经网络,其中一层中的所有神经元都连接到下一层中的所有神经元。
输入呈现在网络的左侧,信息向右传播(或流动)到另一端的输出。由于信息在此处在网络中沿前向传播,因此我们也将此类网络称为前馈神经网络。
输入层和输出层之间的神经元层被称为隐藏层,因为它们无法直接访问。
两个神经元之间的每个连接(在图中用箭头表示)都被赋予一个权重,该权重作用于流经网络的数据,我们稍后将看到。
想开始学习机器学习微积分吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
神经元的数学原理
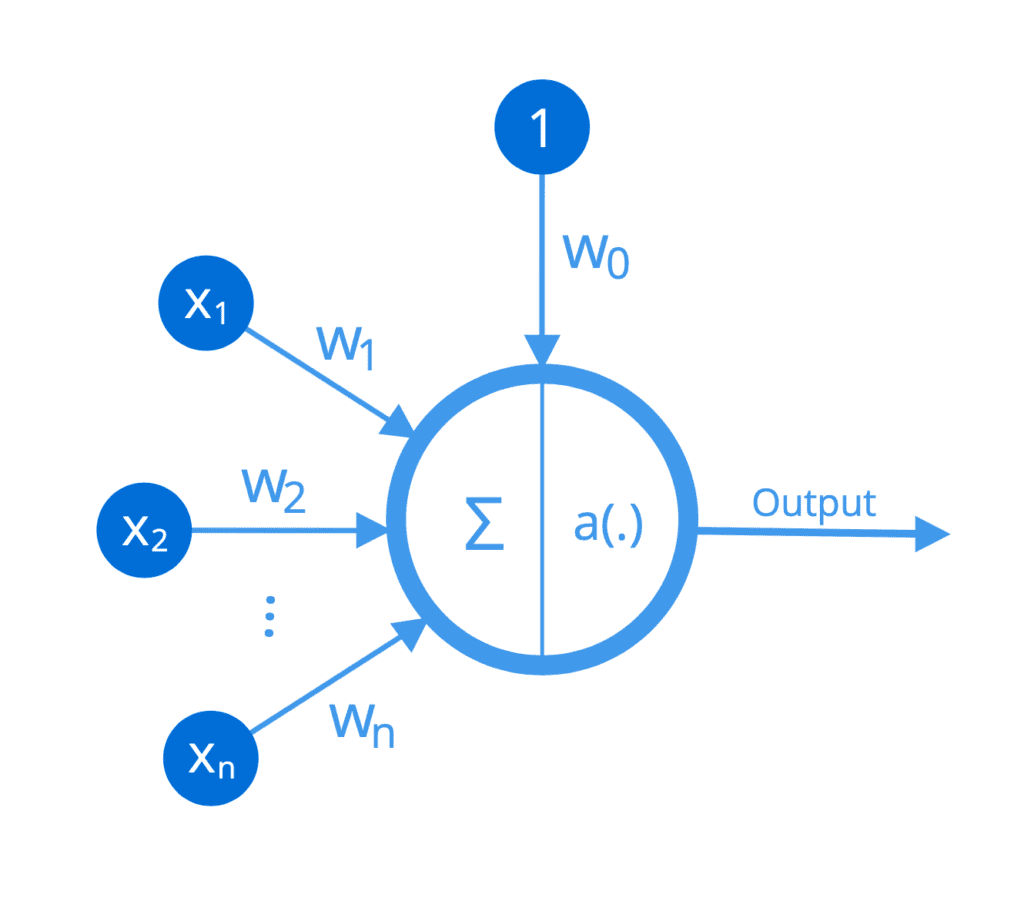
更具体地说,假设一个特定的人工神经元(或 Frank Rosenblatt 最初将其命名为感知器)接收 n 个输入,[x1, ..., xn],其中每个连接都被赋予一个相应的权重,[w1, ..., wn]。
执行的第一个操作是将输入值乘以其对应的权重,并将偏置项 b 添加到它们的和中,从而产生输出 z
z = ((x1 × w1) + (x2 × w2) + … + (xn × wn)) + b
我们可以选择将此操作表示为以下更紧凑的形式:
我们目前执行的这个加权和计算是一个线性操作。如果每个神经元都必须单独执行这个特定的计算,那么神经网络将仅限于学习线性输入-输出映射。
然而,我们可能想要建模的许多现实世界关系都是非线性的,如果我们试图使用线性模型来建模这些关系,那么模型将非常不准确。
– 第77页, 深度学习, 2019。
因此,每个神经元执行第二个操作,通过应用非线性激活函数 a(.) 来转换加权和:
如果我们把偏置项作为一个单独的权重 w0 整合到求和中(注意求和现在从 0 开始),我们可以更紧凑地表示每个神经元执行的操作:
每个神经元执行的操作可以如下所示:
因此,每个神经元可以被认为实现了一个非线性函数,将一组输入映射到输出激活。
训练网络
训练人工神经网络涉及寻找最能模拟数据中模式的权重集。这是一个同时采用反向传播和梯度下降算法的过程。这两种算法都大量使用了微积分。
每次网络向前(或向右)遍历时,可以通过损失函数(例如平方误差和 (SSE))计算网络误差,即网络产生的输出与预期真实值之间的差值。然后,反向传播算法计算此误差对权重变化的梯度(或变化率)。为此,它需要使用链式法则和偏导数。
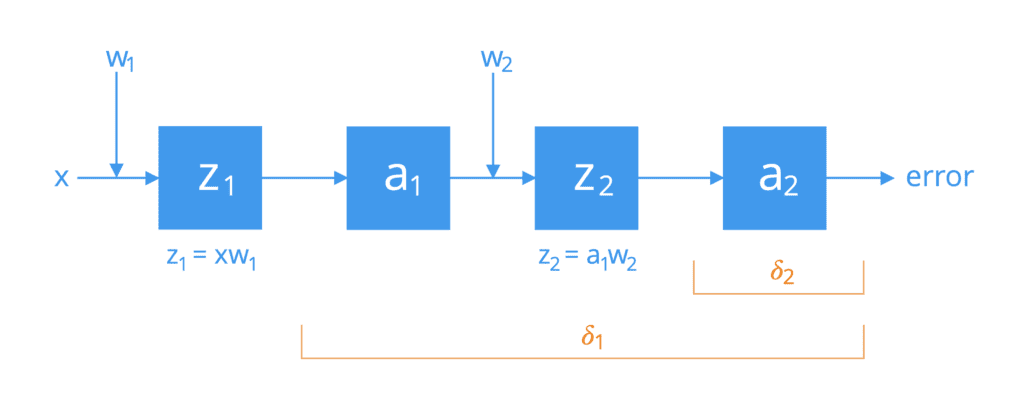
为简单起见,考虑一个由两个神经元通过单个激活路径连接的网络。如果我们将它们分解,我们会发现这些神经元依次执行以下操作:
链式法则的首次应用将网络的整体误差与第二个神经元激活函数 a2 的输入 z2 相关联,并随后与权重 w2 相关联,如下所示
您可能会注意到,链式法则的应用除其他项外,还涉及乘以神经元激活函数对其输入 z2 的偏导数。有不同的激活函数可供选择,例如 sigmoid 函数或 logistic 函数。如果我们将 logistic 函数作为示例,那么它的偏导数将计算如下:
因此,我们可以按以下方式计算 ????2:
这里,t2 是预期的激活值,通过计算 t2 和 a2 之间的差值,我们计算的是网络生成的激活值与预期真实值之间的误差。
由于我们正在计算激活函数的导数,因此它应该在整个实数空间上连续且可微分。在深度神经网络的情况下,误差梯度会在大量隐藏层上反向传播。这可能导致误差信号迅速减小到零,特别是如果导数函数的最大值本身就很小(例如,逻辑函数的倒数最大值为 0.25)。这就是所谓的梯度消失问题。ReLU 函数在深度学习中如此受欢迎地用于缓解这个问题,因为其在其域的正部分中的导数等于 1。
下一个向后的权重位于网络更深处,因此,链式法则的应用可以类似地扩展,以将总误差与权重 w1 连接起来,如下所示
如果再次选择逻辑函数作为激活函数,那么我们可以按以下方式计算 ????1:
一旦我们计算了网络误差相对于每个权重的梯度,就可以应用梯度下降算法来更新每个权重,以便在时间 t+1 进行下一次前向传播。对于权重 w1,使用梯度下降的权重更新规则将指定如下
尽管我们在此处考虑了一个简单的网络,但我们所经历的过程可以扩展到评估更复杂、更深层次的网络,例如卷积神经网络(CNN)。
如果所考虑的网络具有来自多个输入(并可能流向多个输出)的多个分支,则其评估将涉及对每个路径的不同导数链求和,类似于我们之前推导广义链式法则的方式。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
总结
在本教程中,您了解了微积分的各个方面是如何应用于神经网络的。
具体来说,你学到了:
- 人工神经网络组织成神经元和连接层,其中每个连接都被赋予一个权重值。
- 每个神经元都实现一个非线性函数,将一组输入映射到一个输出激活值。
- 在训练神经网络时,反向传播和梯度下降算法大量使用了微积分。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。
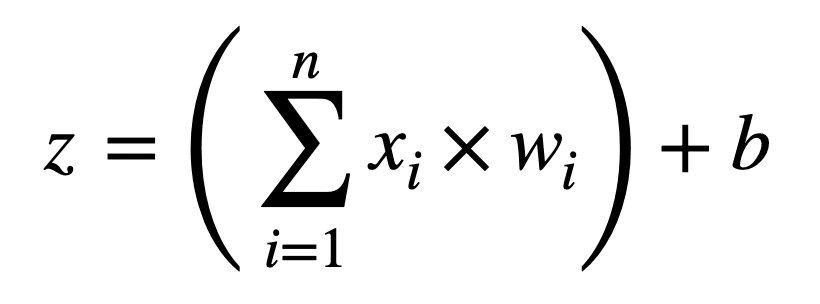
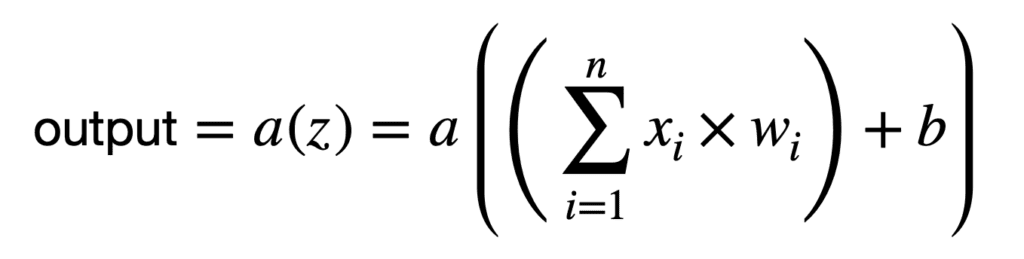
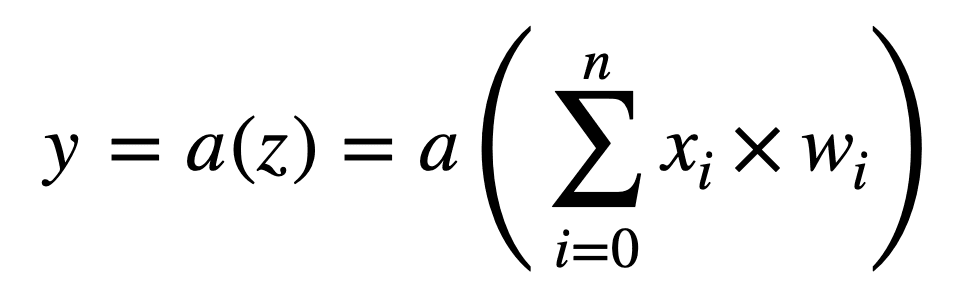
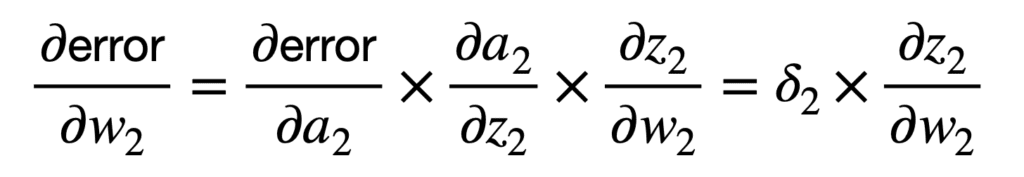

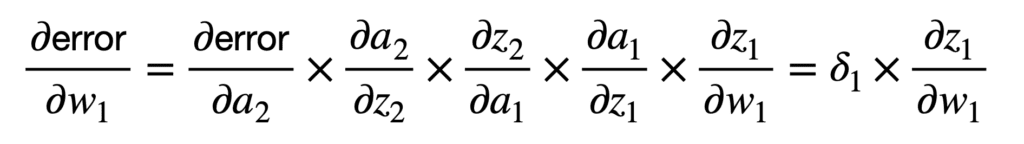
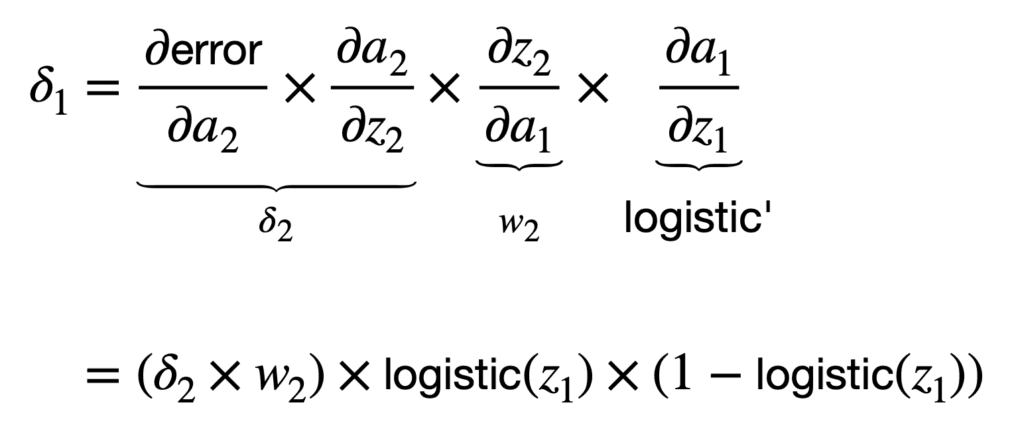
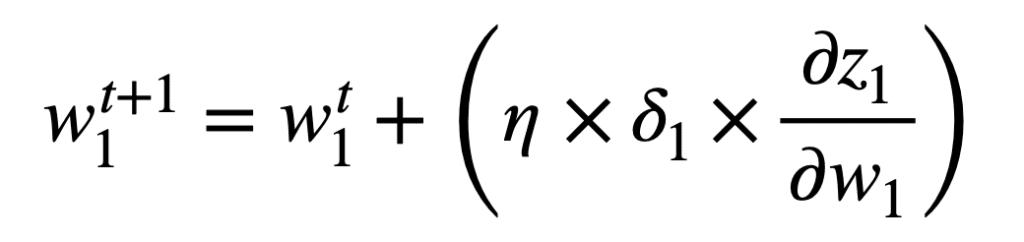







这太棒了!
谢谢。
又一篇好文章。你能从头开始写一篇关于多层感知器神经网络的文章吗?
你觉得这个适合你吗? https://machinelearning.org.cn/implement-perceptron-algorithm-scratch-python/
我一直感到困惑的一点是如何决定一层需要多少个神经元。例如,你如何决定在第一个隐藏层中(如果是一个全连接层)定义多少个神经元?
这里没有经验法则。你需要进行实验和验证。神经网络是一种近似机器。你拥有的神经元越多,你的模型就越有可能更好地近似现实世界来解决你的问题。然而,神经元越多,资源消耗就越大,或者需要更长的时间才能收敛。这里存在一个权衡。
好文章
谢谢。
我目前正在学习深度学习和神经网络。我想知道如何使用梯度下降来训练我的神经网络。
这将有所帮助: https://machinelearning.org.cn/a-gentle-introduction-to-gradient-descent-procedure/
嗨,Joe……谢谢你的问题!以下资源将提供梯度下降优化的介绍。
https://machinelearning.org.cn/gradient-descent-optimization-from-scratch/
此致,
信息量太大了。
感谢您的反馈,AlrawdA!
你好,非常感谢这篇精彩的文章。
我想知道在最后一个公式(权重更新规则)中,应该是减号而不是加号吗?
嗨,Jan……你说的对!感谢您的反馈!
您好,我有一个问题。为了在更改参数时获得新值,我们是应该将斜率项添加到旧值还是从中减去?
嗨,Siddhant……以下资源详细描述了神经网络中反向传播如何更新权重:
https://hmkcode.com/ai/backpropagation-step-by-step/
我在 ????2 处跟不上了:为什么 d(error)/d(a2)=t2-a2?此外,“预期真实值”这个表达没有意义:你预期的是模型输出,但真实值是实际输出。t2-a2 是误差,但我们需要误差对激活函数的偏导数……
嗨,Mamuka……有关反向传播算法数学的更多清晰解释可以在这里找到:
https://365datascience.com/trending/backpropagation/