离散随机变量的概率可以用离散概率分布来概括。
离散概率分布在机器学习中应用广泛,最显著的特点是在二分类和多分类问题的建模中,但也在评估二分类模型性能时发挥作用,例如置信区间计算,以及在自然语言处理中对文本词语分布的建模。
在深度学习神经网络输出层中选择分类任务的激活函数和选择合适的损失函数时,也需要离散概率分布的知识。
离散概率分布在应用机器学习中扮演着重要角色,有一些分布是从业者必须了解的。
在本教程中,您将了解机器学习中使用的离散概率分布。
完成本教程后,您将了解:
- 离散随机变量结果的概率可以用离散概率分布来概括。
- 单个二元结果遵循伯努利分布,而一系列二元结果遵循二项分布。
- 单个分类结果遵循多项伯努利分布,而一系列分类结果遵循多项分布。
通过我的新书《机器学习概率论》**启动您的项目**,其中包括分步教程和所有示例的Python 源代码文件。
让我们开始吧。
- 2020 年 10 月更新:修正了二项分布描述中的一个错字。

机器学习中的离散概率分布
图片由John Fowler提供,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- 离散概率分布
- 伯努利分布
- 二项分布
- 多项伯努利分布
- 多项分布
离散概率分布
随机变量是随机过程产生的量。
离散随机变量是一种随机变量,它可以从有限的特定结果集中取值。机器学习中最常用的两种离散随机变量是二元变量和分类变量。
- 二元随机变量:x ∈ {0, 1}
- 分类随机变量:x ∈ {1, 2, …, K}。
二元随机变量是离散随机变量,其有限结果集为 {0, 1}。分类随机变量是离散随机变量,其有限结果集为 {1, 2, …, K},其中 K 是唯一结果的总数。
离散随机变量的每个结果或事件都有一个概率。
离散随机变量的事件与其概率之间的关系称为离散概率分布,并由概率质量函数(简称 PMF)概括。
对于可以排序的结果,事件的概率小于或等于给定值由累积分布函数(简称 CDF)定义。CDF 的逆称为百分点函数,它将给出小于或等于给定概率的离散结果。
- PMF:概率质量函数,返回给定结果的概率。
- CDF:累积分布函数,返回小于或等于给定结果值的概率。
- PPF:百分点函数,返回小于或等于给定概率的离散值。
有许多常见的离散概率分布。
最常见的是伯努利分布和多项伯努利分布,分别用于二元和分类离散随机变量,以及二项分布和多项分布,它们将每个分布推广到多个独立试验。
- 二元随机变量:伯努利分布
- 二元随机变量序列:二项分布
- 分类随机变量:多项伯努利分布
- 分类随机变量序列:多项分布
在下面的部分中,我们将依次仔细研究这些分布。
您可能还想探索其他离散概率分布,包括泊松分布和离散均匀分布。
想学习机器学习概率吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
伯努利分布
伯努利分布是一种离散概率分布,它涵盖事件只有 0 或 1 两种二元结果的情况。
- x ∈ {0, 1}
“伯努利试验”是一种结果遵循伯努利分布的实验或情况。该分布和试验以瑞士数学家雅各布·伯努利的名字命名。
伯努利试验的一些常见例子包括:
- 抛掷一次硬币,结果可能为正面 (0) 或反面 (1)。
- 单次出生,结果为男孩 (0) 或女孩 (1)。
机器学习中伯努利试验的一个常见例子可能是对单个样本进行二元分类,将其分为第一类 (0) 或第二类 (1)。
该分布可以用一个变量 p 来概括,该变量定义了结果为 1 的概率。给定此参数,每个事件的概率可以按如下方式计算:
- P(x=1) = p
- P(x=0) = 1 – p
在抛掷一枚公平硬币的情况下,p 的值将为 0.5,每个结果的概率为 50%。
二项分布
多次独立伯努利试验的重复称为伯努利过程。
伯努利过程的结果将遵循二项分布。因此,伯努利分布将是只有一次试验的二项分布。
伯努利过程的一些常见例子包括:
- 一系列独立的硬币抛掷。
- 一系列独立的出生。
机器学习算法在二元分类问题上的性能可以分析为伯努利过程,其中模型对测试集中一个示例的预测是伯努利试验(正确或不正确)。
二项分布总结了给定次数的伯努利试验 k 中成功的次数,其中每次试验的成功概率为 p。
我们可以用一个伯努利过程来证明这一点,其中成功的概率是 30% 或 P(x=1) = 0.3,总试验次数是 100 (k=100)。
我们可以通过随机生成案例来模拟伯努利过程,并计算给定试验次数内的成功次数。这可以通过binomial() NumPy 函数来实现。该函数以总试验次数和成功概率作为参数,并返回一次模拟中所有试验的成功结果次数。
|
1 2 3 4 5 6 7 8 |
# 模拟二项过程并计算成功次数的示例 from numpy.random import binomial # 定义分布的参数 p = 0.3 k = 100 # 运行一次模拟 success = binomial(k, p) print('总成功次数: %d' % success) |
根据所选参数(k * p 或 100 * 0.3),我们预计 100 个案例中有 30 个会成功。
每次运行代码时都会生成不同的 100 次试验的随机序列,因此您的具体结果会有所不同。请尝试多次运行示例。
在这种情况下,我们看到成功试验的次数略低于预期的 30 次。
|
1 |
总成功次数:28 |
我们可以使用binom.stats() SciPy 函数来计算此分布的矩,特别是期望值或均值以及方差。
|
1 2 3 4 5 6 7 8 |
# 计算二项分布的矩 from scipy.stats import binom # 定义分布的参数 p = 0.3 k = 100 # 计算矩 mean, var, _, _ = binom.stats(k, p, moments='mvsk') print('均值=%.3f, 方差=%.3f' % (mean, var)) |
运行示例会报告分布的期望值,即 30,正如我们所预期的那样,以及方差为 21,如果我们计算平方根,则标准差约为 4.5。
|
1 |
均值=30.000,方差=21.000 |
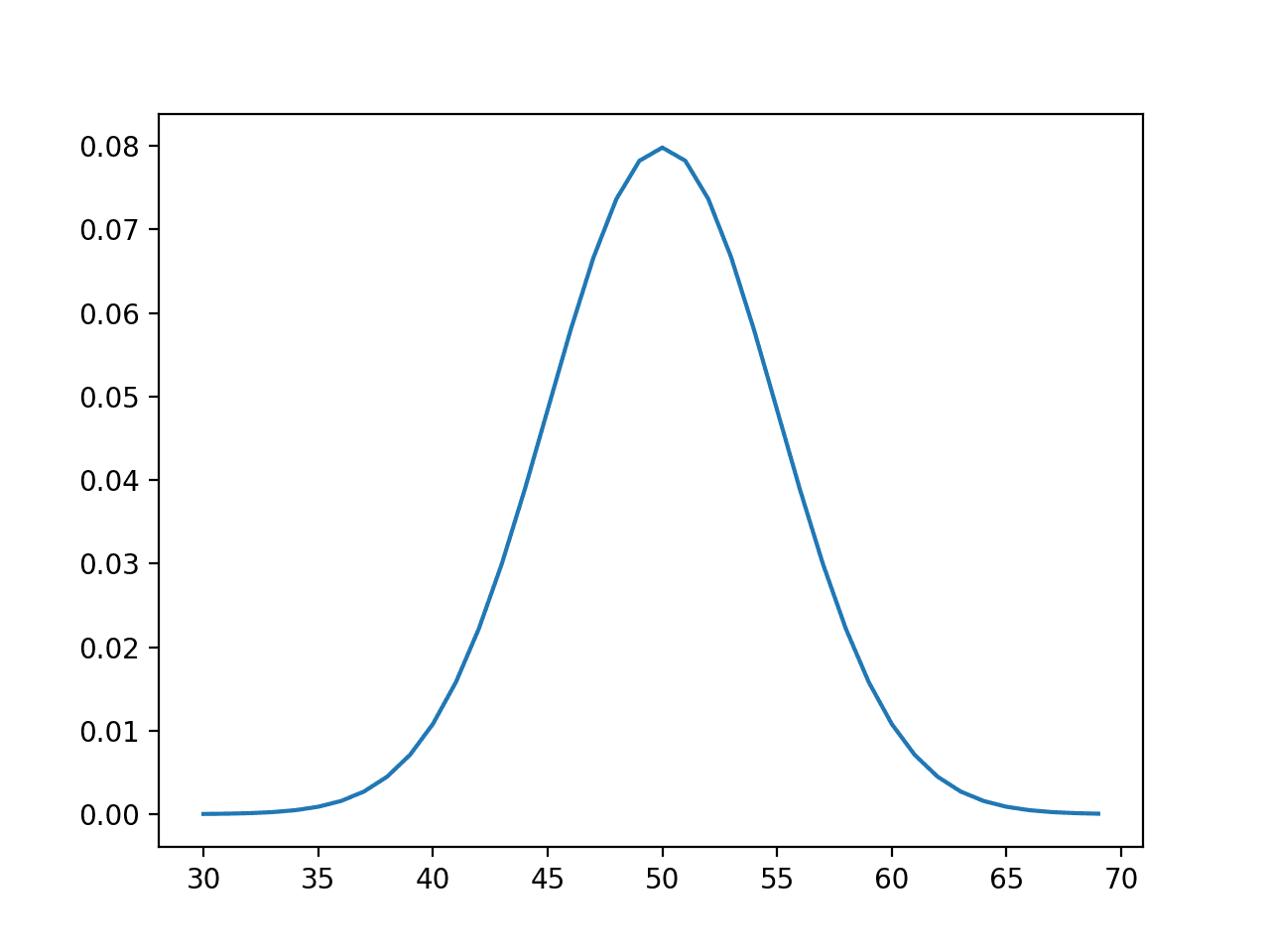
我们可以使用概率质量函数来计算一系列试验中不同成功次数的可能性,例如 10、20、30 到 100。
我们预计 30 次成功结果的概率最高。
|
1 2 3 4 5 6 7 8 9 10 |
# 使用二项分布的 pmf 的示例 from scipy.stats import binom # 定义分布的参数 p = 0.3 k = 100 # 定义分布 dist = binom(k, p) # 计算 n 次成功的概率 for n in range(10, 110, 10): print('%d 次成功的概率: %.3f%%' % (n, dist.pmf(n)*100)) |
运行示例定义了二项分布,并计算了 [10, 100] 范围内每组 10 次成功结果的概率。
概率乘以 100 以百分比表示,我们可以看到 30 次成功结果的概率最高,约为 8.6%。
|
1 2 3 4 5 6 7 8 9 10 |
10 次成功的概率: 0.000% 20 次成功的概率: 0.758% 30 次成功的概率: 8.678% 40 次成功的概率: 0.849% 50 次成功的概率: 0.001% 60 次成功的概率: 0.000% 70 次成功的概率: 0.000% 80 次成功的概率: 0.000% 90 次成功的概率: 0.000% 100 次成功的概率: 0.000% |
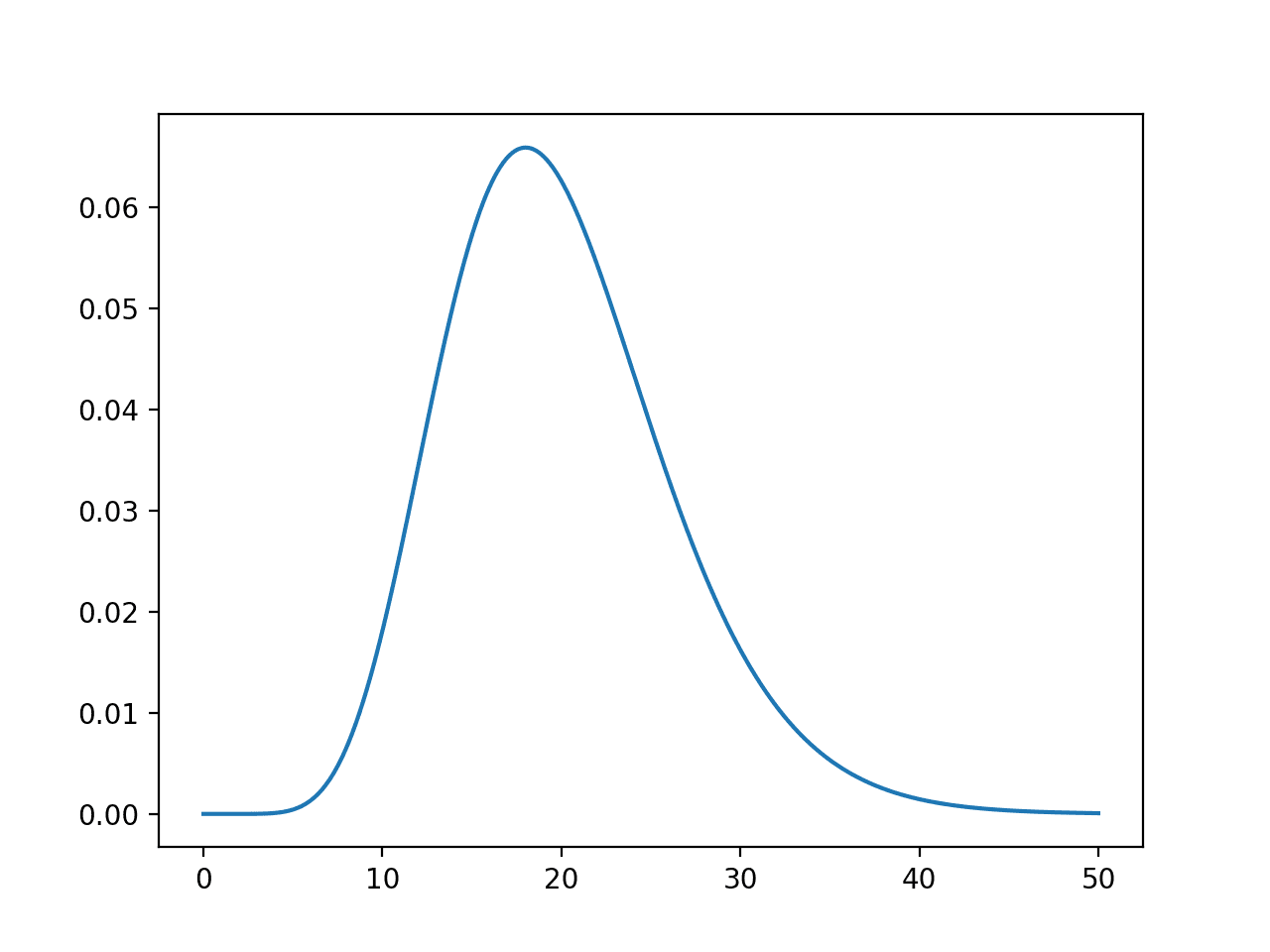
鉴于一次试验的成功概率为 30%,我们预计 100 次试验中成功次数为 50 次或更少的概率接近 100%。我们可以使用累积分布函数来计算,如下所示。
|
1 2 3 4 5 6 7 8 9 10 |
# 使用二项分布的 cdf 的示例 from scipy.stats import binom # 定义分布的参数 p = 0.3 k = 100 # 定义分布 dist = binom(k, p) # 计算成功次数小于等于 n 的概率 for n in range(10, 110, 10): print('%d 次成功的概率: %.3f%%' % (n, dist.cdf(n)*100)) |
运行示例会打印 [10, 100] 范围内每组 10 次成功次数,以及 100 次试验中达到或少于该次数的成功概率。
正如预期的那样,50 次或更少的成功次数涵盖了此分布中预计发生成功次数的 99.999%。
|
1 2 3 4 5 6 7 8 9 10 |
10 次成功的概率: 0.000% 20 次成功的概率: 1.646% 30 次成功的概率: 54.912% 40 次成功的概率: 98.750% 50 次成功的概率: 99.999% 60 次成功的概率: 100.000% 70 次成功的概率: 100.000% 80 次成功的概率: 100.000% 90 次成功的概率: 100.000% 100 次成功的概率: 100.000% |
多项伯努利分布
多项伯努利分布,也称为分类分布,涵盖事件将有 K 个可能结果之一的情况。
- x ∈ {1, 2, 3, …, K}
它是伯努利分布从二元变量到分类变量的推广,其中伯努利分布的案例数 K 设置为 2,即 K=2。
一个遵循多项伯努利分布的常见例子是:
- 单次掷骰子,结果在 {1, 2, 3, 4, 5, 6} 中,例如 K=6。
机器学习中多项伯努利分布的一个常见例子可能是将单个样本多类别分类到 K 个类别之一,例如,虹膜花的三个不同物种之一。
该分布可以通过 p1 到 pK 的 K 个变量来概括,每个变量定义了从 1 到 K 的给定分类结果的概率,并且所有概率之和为 1.0。
- P(x=1) = p1
- P(x=2) = p2
- P(x=3) = p3
- …
- P(x=K) = pK
在单次掷骰子的情况下,每个值的概率将为 1/6,或约 0.166,或约 16.6%。
多项分布
多次独立多项伯努利试验的重复将遵循多项分布。
多项分布是具有 K 个结果的离散变量的二项分布的推广。
多项过程的一个例子包括一系列独立的掷骰子。
多项分布的一个常见例子是自然语言处理领域中,文本文档中单词的出现次数。
多项分布由一个离散随机变量概括,该变量具有 K 个结果,每个结果的概率从 p1 到 pK,以及 k 次连续试验。
我们可以用一个有 3 个类别(K=3),概率相等(p=33.33%)和 100 次试验的小例子来演示。
首先,我们可以使用multinomial() NumPy 函数来模拟 100 次独立试验,并总结事件在每个给定类别中出现的次数。该函数接受试验次数和每个类别的概率作为列表。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 |
# 模拟多项过程的示例 from numpy.random import multinomial # 定义分布的参数 p = [1.0/3.0, 1.0/3.0, 1.0/3.0] k = 100 # 运行一次模拟 cases = multinomial(k, p) # 总结案例 for i in range(len(cases)): print('案例 %d: %d' % (i+1, cases[i])) |
我们预计每个类别大约有 33 个事件。
运行示例会报告每个案例和事件的数量。
每次运行代码时都会生成不同的 100 次试验的随机序列,因此您的具体结果会有所不同。请尝试多次运行示例。
在这种情况下,我们看到案例分布范围从 37 到 30。
|
1 2 3 |
案例 1: 37 案例 2: 33 案例 3: 30 |
我们可能期望理想情况下的 100 次试验会分别产生事件 1、2 和 3 的 33、33 和 34 个案例。
我们可以使用概率质量函数或multinomial.pmf() SciPy 函数来计算这种特定组合在实践中发生的概率。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 计算每种类型给定事件数量的概率 from scipy.stats import multinomial # 定义分布的参数 p = [1.0/3.0, 1.0/3.0, 1.0/3.0] k = 100 # 定义分布 dist = multinomial(k, p) # 定义 100 次试验中特定数量的结果 cases = [33, 33, 34] # 计算该案例的概率 pr = dist.pmf(cases) # 以百分比形式打印 print('案例=%s, 概率: %.3f%%' % (cases, pr*100)) |
运行该示例报告了 [33, 33, 34] 这种理想案例组合的概率,对于每种事件类型,其概率小于 1%。
|
1 |
案例=[33, 33, 34], 概率: 0.813% |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
API
文章
总结
在本教程中,您了解了机器学习中使用的离散概率分布。
具体来说,你学到了:
- 离散随机变量结果的概率可以用离散概率分布来概括。
- 单个二元结果遵循伯努利分布,而一系列二元结果遵循二项分布。
- 单个分类结果遵循多项伯努利分布,而一系列分类结果遵循多项分布。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



这些课程内容全面,我非常喜欢。我有一些概率论背景,这可能是理解起来比较容易的原因。到目前为止,我能够跟上,但我正在尝试使用 Anaconda 上的 Jupyter Notebook 运行 Python 代码。我还没有启动 Notebook。
我能够使用 Jupyter notebook 运行代码。结果是相似的。谢谢。
干得好!
谢谢!
也许可以尝试在命令行运行示例,方法如下
https://machinelearning.org.cn/faq/single-faq/how-do-i-run-a-script-from-the-command-line
谢谢
不客气!
嗨,Jason,
如果我没错,多项伯努利分布部分的公式是不是有错别字?
该分布可以用 p**(K)** 个变量从 p1 到 pK 来概括,每个变量定义了从 1 到 K 的给定分类结果的概率,并且所有概率之和为 1.0。
P(x=1) = p1
P(x=2) = p1 **(p2)**
P(x=3) = p3
…
P(x=K) = pK
谢谢!
我没看懂,你觉得错误具体是什么?
这显然是个错别字
我明白了。谢谢,已修复!
你好,
是否有可能计算一个离散因变量的多项分布,该因变量在一个数据集中依赖于 n 个独立的连续变量?
抱歉,我不确定您在问什么,听起来像是一个联合概率分布——我们无法计算,因为我们无法访问所有事件组合。
在您的多项分布示例中,我们看到 37、33、30。是什么决定了每次模拟迭代与期望值 (33) 的距离?
例如,在 100 次模拟试验中,生成的数值可能有一个范围限制——(可能是 27 到 40?),是什么决定了这些限制?如果我想生成具有更极端值的试验(例如 20 和 50?),但所有试验的平均值仍然接近 33/34,那该怎么办?
我问这个问题是因为所使用的 0.3、0.3、0.3 概率可能是根据经验数据计算出的平均值,如果数据具有较大的方差且平均值为 0.3,那么模拟可能无法生成您在数据中观察到的这些极端值。
领域,即领域特定——最初生成数据的过程。
谢谢!那么,在多项式函数中是否有设置方差的选项,可以调整每个模拟组内的变异性,这样我就可以模拟更极端的值,但平均值仍然接近 33/34?
或者有没有其他 Python 函数可以模拟这类过程?
我相信 numpy/scipy 提供了用于采样任意函数的函数。我建议您查阅 API 文档。
嗨,Jason,
让我们从 Kaggle 获取蘑菇分类数据集。
有一个分类特征“bruises”(瘀伤)。它有两个类别:f 和 t。
我们可以说“bruises”遵循伯努利分布吗?
因为
1.它有两个结果,即 f 和 t。
2.两个结果中的每一个都有固定的发生概率,概率(f) + 概率(t) = 1。
3.试验完全相互独立。
请参考以下代码:
print(df[‘bruises’].value_counts())
print(df[‘bruises’].value_counts(normalize=True))
print(df[‘bruises’].value_counts(normalize=True)[0] + df[‘bruises’].value_counts(normalize=True)[1])
输出
f 4748
t 3376
Name: bruises, dtype: int64
f 0.584441
t 0.415559
Name: bruises, dtype: float64
1.0
但是我不明白“bruises”特征的实验是如何进行的?
我之所以认为“bruises”遵循伯努利分布,是因为它有两个类别,并且概率之和为 1。
请纠正我的理解。
您可以考虑任何数据集中的性别特征,那么性别可以是伯努利分布吗?
嗨,Jason,
我是数据科学新手,在进行 EDA 时,我曾想知道分类特征遵循哪些不同类型的分布(就像数值特征遵循正态、对数等)。
Kaggle 的蘑菇分类数据集中有一个分类特征“bruises”。
根据我的理解,它遵循伯努利分布。让我告诉你原因。
1.它只有两个结果/值,即 t 和 f。
2.两个结果中的每一个都有固定的发生概率。概率(t) + 概率(f) = 1.0。
3.试验完全相互独立。
请参考以下代码。
print(df[‘bruises’].value_counts())
print(df[‘bruises’].value_counts(normalize=True))
print(df[‘bruises’].value_counts(normalize=True)[0] + df[‘bruises’].value_counts(normalize=True)[1])
输出
f 4748
t 3376
Name: bruises, dtype: int64
f 0.584441
t 0.415559
Name: bruises, dtype: float64
1.0
我之所以得出它是伯努利分布的结论,是因为它有两个值,并且总概率为 1,但我不知道这里什么是实验(它可能是“bruises”得到 f 或 t)??
请告诉我我的理解是否正确。
如果我在这里的理解是正确的,那意味着性别也遵循伯努利分布。
嗨,Deva…您可能会对以下内容感兴趣
https://machinelearning.org.cn/what-are-probability-distributions/
感谢您的回复。
是的,我读过同样的文章。
但是您能澄清我对上述问题的理解吗?
这将非常有帮助。
嗨,Jason,
如果特征有许多名义类别(如多项分布),但 PMF 之和不等于 1 怎么办?
您能指导我这种特征遵循哪种类型的分布吗?