高阶导数可以捕捉函数的一阶导数本身无法捕捉的信息。
一阶导数可以捕捉重要信息,例如变化率,但它们本身无法区分局部最小值或局部最大值,因为在这两种情况下变化率都为零。一些优化算法通过利用高阶导数来解决这个限制,例如在牛顿法中,二阶导数用于达到优化函数的局部最小值。
在本教程中,您将学习如何计算高阶单变量和多变量导数。
完成本教程后,您将了解:
- 如何计算单变量函数的高阶导数。
- 如何计算多变量函数的高阶导数。
- 二阶导数如何通过二阶优化算法在机器学习中得到利用。
让我们开始吧。

高阶导数
照片来源:Jairph,部分权利保留。
教程概述
本教程分为三个部分;它们是:
- 单变量函数的高阶导数
- 多变量函数的高阶导数
- 在机器学习中的应用
单变量函数的高阶导数
除了我们已经看到可以提供函数重要信息(例如其瞬时变化率)的一阶导数之外,高阶导数也同样有用。例如,二阶导数可以测量运动物体的加速度,或者它可以帮助优化算法区分局部最大值和局部最小值。
计算单变量函数的高阶(二阶、三阶或更高阶)导数并不困难。
函数的二阶导数只是其一阶导数的导数。三阶导数是二阶导数的导数,四阶导数是三阶导数的导数,依此类推。
——《傻瓜微积分》第147页,2016年。
因此,计算高阶导数只需重复对函数进行求导。为此,我们可以简单地应用我们对幂法则的知识。让我们以函数 f(x) = x3 + 2x2 – 4x + 1 为例。那么
一阶导数:f’(x) = 3x2 + 4x – 4
二阶导数:f’’(x) = 6x + 4
三阶导数:f’’’(x) = 6
四阶导数:f (4)(x) = 0
五阶导数:f (5)(x) = 0 等等
我们在这里所做的是,首先对 f(x) 应用幂法则以获得其一阶导数 f’(x),然后对一阶导数应用幂法则以获得二阶导数,依此类推。随着求导的重复应用,导数最终将变为零。
乘积法则和商法则的应用在获得高阶导数方面仍然有效,但随着阶数的增加,它们的计算可能会变得越来越复杂。广义莱布尼茨法则通过将乘积法则推广到以下形式,简化了这方面的任务:
这里,项 n! / k!(n – k)! 是二项式定理中的二项式系数,而 f (k) 和 g(k) 分别表示函数 f 和 g 的 k 阶导数。
因此,通过广义莱布尼茨法则求一阶和二阶导数(分别代入 n = 1 和 n = 2)得到
(fg)(1) = (fg)’ = f (1) g + f g(1)
(fg)(2) = (fg)’’ = f (2) g + 2f (1) g(1) + f g(2)
请注意乘积法则中定义的熟悉的一阶导数。莱布尼茨法则也可以用来寻找有理函数的高阶导数,因为商可以有效地表示成 f g-1 的乘积形式。
多变量函数的高阶导数
多变量函数的高阶偏导数的定义与单变量情况类似:当 n > 1 时, n 阶偏导数通过计算 (n – 1) 阶偏导数的偏导数来得到。例如,对一个二元函数取二阶偏导数会得到四个二阶偏导数:两个**自身**偏导数 fxx 和 fyy,以及两个**混合**偏导数 fxy 和 fyx。
要进行“求导”,我们必须对 x 或 y 求偏导数,有四种方法:先 x 后 x,先 x 后 y,先 y 后 x,先 y 后 y。
——《单变量和多变量微积分》第371页,2020年。
我们来看多变量函数 f(x, y) = x2 + 3xy + 4y2,我们希望求其二阶偏导数。这个过程首先要找到其一阶偏导数: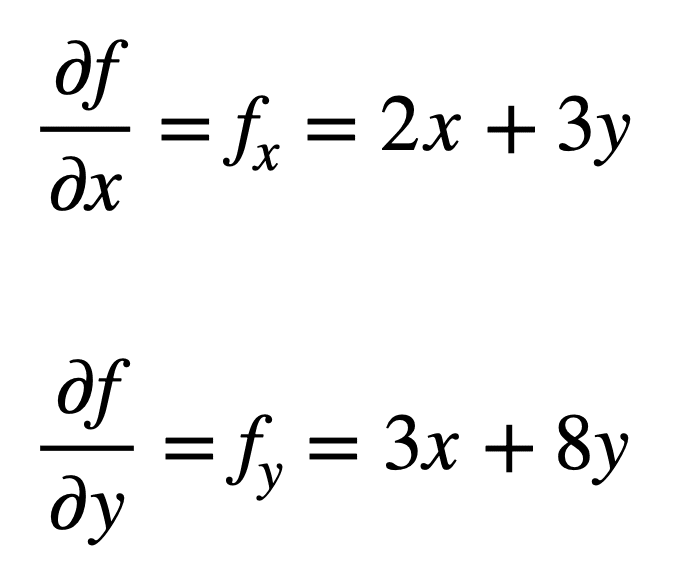
然后通过重复求偏导数(即对偏导数求偏导数)的过程,找出四个二阶偏导数。**自身**偏导数最直接,因为我们只需第二次重复对 x 或 y 求偏导数的过程。
之前找到的 fx(即对 x 的偏导数)的混合偏导数,通过对结果求对 y 的偏导数得到 fxy。类似地,对 fy 求对 x 的偏导数,得到 fyx:
交叉偏导数得到相同的结果并非偶然。这是由克莱罗定理定义的,该定理指出只要交叉偏导数是连续的,它们就相等。
想开始学习机器学习微积分吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
在机器学习中的应用
在机器学习中,主要使用的是二阶导数。我们之前提到过,二阶导数可以提供一阶导数本身无法捕捉的信息。具体来说,它可以告诉我们一个临界点是局部最小值还是局部最大值(分别基于二阶导数是大于还是小于零),而在一阶导数在这两种情况下都将为零。
有几种利用这些信息的**二阶**优化算法,其中之一就是牛顿法。
另一方面,二阶信息允许我们对目标函数进行二次近似,并近似正确的步长以达到局部最小值……
——《优化算法》第87页,2019年。
在单变量情况下,牛顿法使用二阶泰勒级数展开来对目标函数上的某个点进行二次近似。牛顿法的更新规则是通过将导数设置为零并求解根来获得的,它涉及一个除以二阶导数的运算。如果将牛顿法扩展到多变量优化,导数将被梯度替换,而二阶导数的倒数将被海森矩阵的逆替换。
我们将在单独的教程中介绍海森矩阵和泰勒级数近似,它们都利用了高阶导数。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 单变量和多变量微积分, 2020.
- 微积分傻瓜书, 2016.
- 深度学习, 2017.
- 优化算法, 2019.
总结
在本教程中,您学习了如何计算高阶单变量和多变量导数。
具体来说,你学到了:
- 如何计算单变量函数的高阶导数。
- 如何计算多变量函数的高阶导数。
- 二阶优化算法如何在机器学习中利用二阶导数。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。
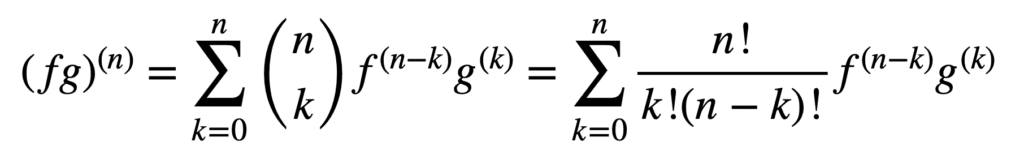
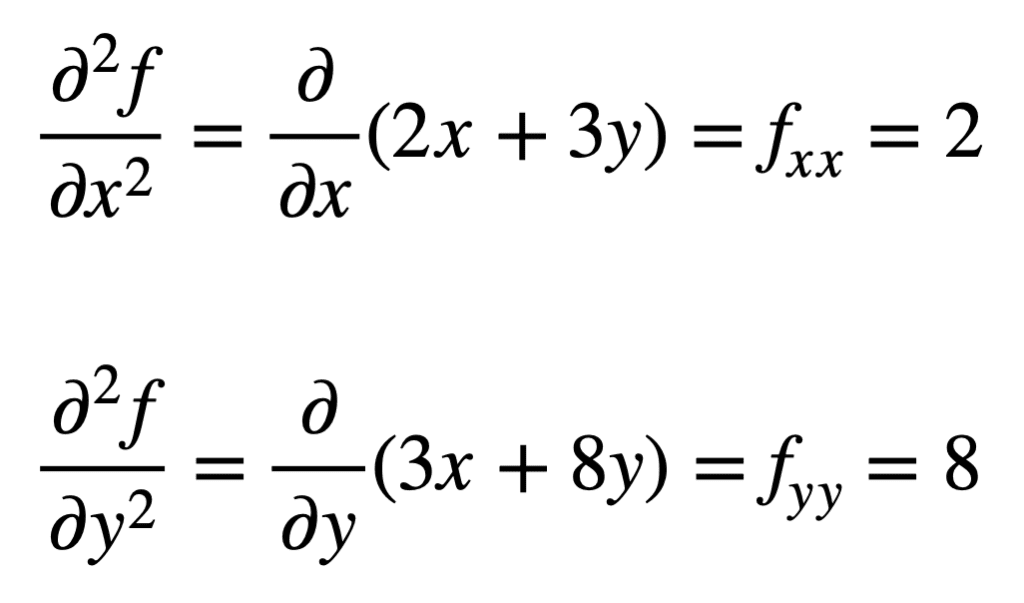
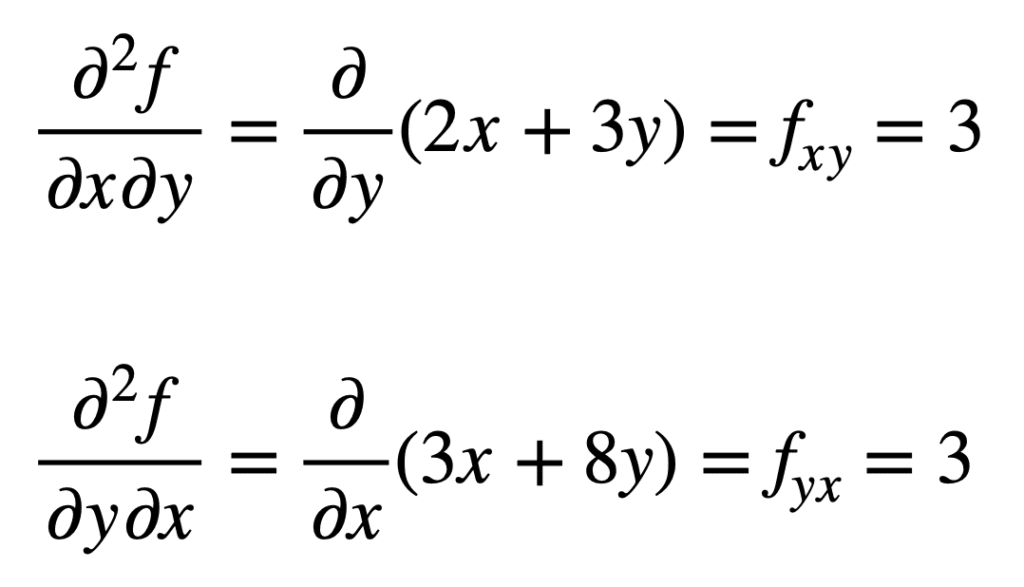






清晰简洁。对于理解二阶导数及其用途非常有帮助。谢谢!
很棒的反馈!