拉格朗日乘数法：支持向量机背后的理论（第2部分：非线性可分情况）

本教程是拉格朗日乘数法：支持向量机背后的理论（第1部分：可分情况）的延伸，并解释了不可分情况。在实际问题中，正负训练样本可能无法被线性决策边界完全分离。本教程解释了如何构建一个容忍一定数量错误的软间隔。

在本教程中，我们将介绍线性SVM的基础知识。我们不会详细介绍使用核技巧推导出的非线性SVM。内容足以理解SVM分类器背后的基本数学模型。

完成本教程后，您将了解：

• 软间隔的概念
• 如何在允许分类错误的同时最大化间隔
• 如何制定优化问题并计算拉格朗日对偶

让我们开始吧。

拉格朗日乘数法：支持向量机背后的理论（第2部分：不可分情况）。
图片作者 Shakeel Ahmad，保留部分权利。

教程概述

本教程分为两部分；它们是：

1. 正负样本不可线性分离情况下SVM问题的解
   1. 分离超平面和相应的宽松约束
   2. 用于寻找软间隔的二次优化问题
2. 一个工作示例

先决条件

本教程假设您已经熟悉以下主题。您可以点击各个链接以获取更多信息。

• 优化/数学规划简明介绍
• 拉格朗日乘数法入门
• 带不等式约束的拉格朗日乘数法
• 拉格朗日乘数法：支持向量机背后的理论（第1部分：可分情况）)

本教程中使用的符号

这是第1部分的延续，因此将使用相同的符号。

• $m$: 总训练点数
• $x$: 数据点，一个$n$维向量。每个维度由j索引。
• $x^+$: 正例
• $x^-$: 负例
• $i$: 用于索引训练点的下标。$0 \leq i < m$
• $j$: 索引数据点维度的下标。$1 \leq j \leq n$
• $t$: 数据点的标签。它是一个m维向量
• $T$: 转置运算符
• $w$: 权重向量，表示超平面的系数。它是一个$n$维向量
• $\alpha$: 拉格朗日乘数向量，一个$m$维向量
• $\mu$: 拉格朗日乘数向量，也是一个$m$维向量
• $\xi$: 分类误差。一个$m$维向量

分离超平面与放宽约束

让我们找到正负样本之间的分离超平面。回顾一下，分离超平面由以下表达式给出，其中\(w_j\)是系数，\(w_0\)是确定超平面与原点距离的任意常数。

$$
w^T x_i + w_0 = 0
$$

由于我们允许正负样本位于超平面的错误一侧，我们有了一组宽松的约束。定义 $\xi_i \geq 0, \forall i$，对于正例，我们要求

$$
w^T x_i^+ + w_0 \geq 1 – \xi_i
$$

对于负例，我们同样要求

$$
w^T x_i^- + w_0 \leq -1 + \xi_i
$$

通过使用类别标签 $t_i \in \{-1,+1\}$，将上述两个约束结合起来，我们得到所有点的以下约束

$$
t_i(w^T x_i + w_0) \geq 1 – \xi_i
$$

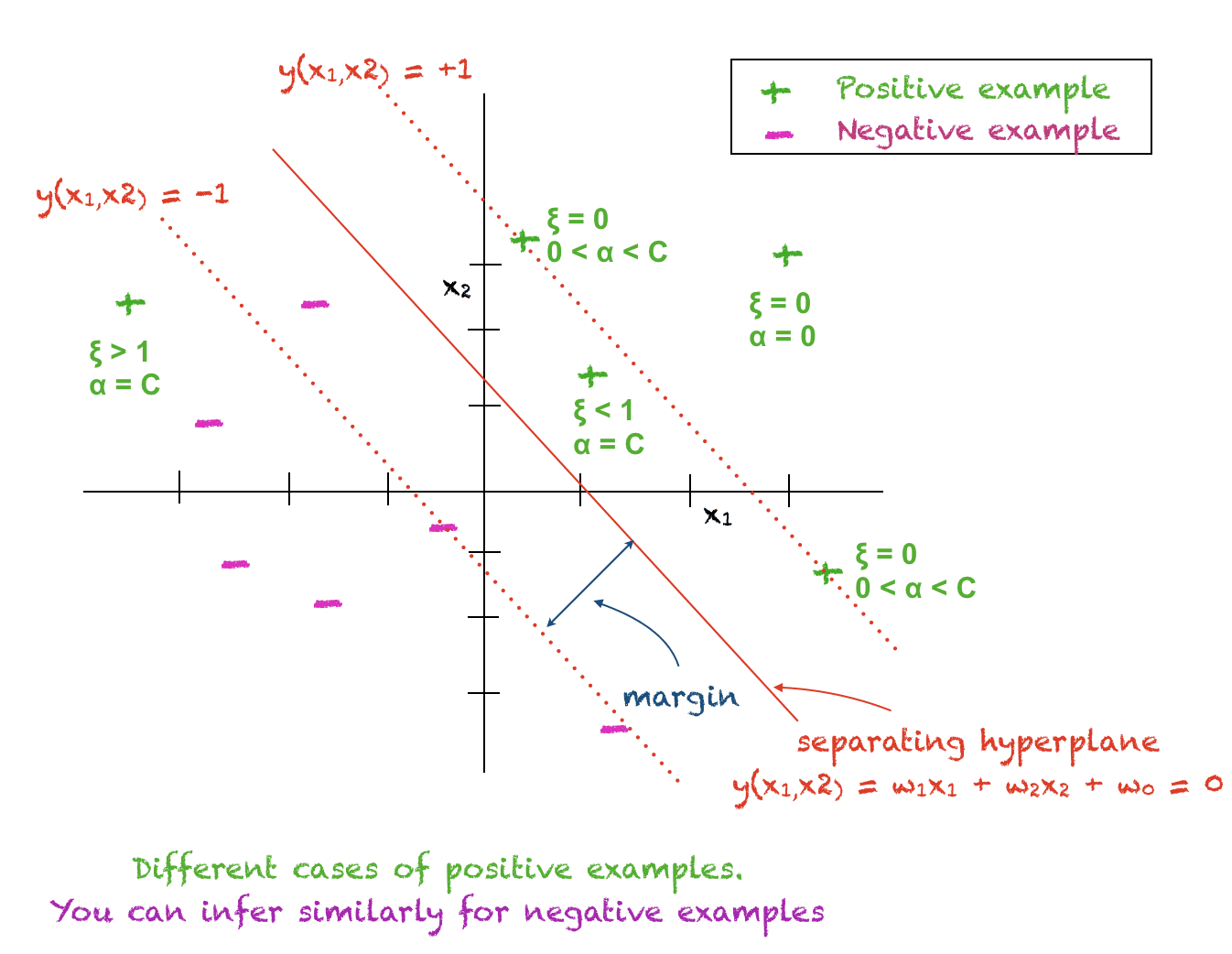
变量 $\xi$ 允许我们的模型具有更大的灵活性。它具有以下解释：

1. $\xi_i =0$: 这意味着$x_i$被正确分类，并且该数据点位于超平面的正确一侧，并且远离间隔。
2. $0 < \xi_i < 1$: 当满足此条件时，$x_i$位于超平面的正确一侧，但在间隔内部。
3. $\xi_i > 0$: 满足此条件意味着$x_i$被错误分类。

因此，$\xi$量化了训练点分类中的错误。我们可以将软错误定义为

$$
E_{soft} = \sum_i \xi_i
$$

二次规划问题

我们现在可以制定目标函数及其约束。我们仍然希望最大化间隔，即最小化权重向量的范数。同时，我们还希望尽可能减小软误差。因此，现在我们的新目标函数由以下表达式给出，其中$C$是用户定义的常数，表示惩罚因子或正则化常数。

$$
\frac{1}{2}||w||^2 + C \sum_i \xi_i
$$

因此，整个二次规划问题由以下表达式给出

$$
\min_w \frac{1}{2}||w||^2 + C \sum_i \xi_i \;\text{ 使得 } t_i(w^Tx_i+w_0) \geq +1 – \xi_i, \forall i \; \text{ 且 } \xi_i \geq 0, \forall i
$$

C，即正则化常数的作用

为了理解惩罚因子$C$，考虑乘积项 $C \sum_i \xi_i$，它必须最小化。如果C保持较大，则软间隔 $\sum_i \xi_i$ 将自动变小。如果$C$接近于零，则我们允许软间隔变大，从而使总乘积变小。

简而言之，较大的$C$值意味着我们对错误进行高惩罚，因此不允许我们的模型在分类中犯太多错误。较小的$C$值允许错误增加。

通过拉格朗日乘数法求解

让我们使用拉格朗日乘数法来解决我们之前提出的二次规划问题。拉格朗日函数由以下公式给出

$$
L(w, w_0, \alpha, \mu) = \frac{1}{2}||w||^2 + \sum_i \alpha_i\big(t_i(w^Tx_i+w_0) – 1 + \xi_i\big) – \sum_i \mu_i \xi_i
$$

为了解决上述问题，我们设置以下条件
\begin{equation}
\frac{\partial L}{ \partial w} = 0, \\
\frac{\partial L}{ \partial \alpha} = 0, \\
\frac{\partial L}{ \partial w_0} = 0, \\
\frac{\partial L}{ \partial \mu} = 0 \\
\end{equation}

解上述方程得到
$$
w = \sum_i \alpha_i t_i x_i
$$
和
$$
0= C – \alpha_i – \mu_i
$$

将上述结果代入拉格朗日函数，得到以下优化问题，也称为对偶问题

$$
L_d = -\frac{1}{2} \sum_i \sum_k \alpha_i \alpha_k t_i t_k (x_i)^T (x_k) + \sum_i \alpha_i
$$

我们必须在以下约束下最大化上述函数

\begin{equation}
\sum_i \alpha_i t_i = 0 \\ \text{ 且 }
0 \leq \alpha_i \leq C, \forall i
\end{equation}

类似于可分情况，我们得到了一个以拉格朗日乘数表示的$w$的表达式。目标函数不包含$w$项。每个数据点都关联着一个拉格朗日乘数$\alpha$和$\mu$。

数学模型的解释和$w_0$的计算

对于每个训练数据点 $x_i$，以下情况成立：

• $\alpha_i = 0$: 第 i 个训练点位于超平面的正确一侧，远离间隔。此点在测试点分类中不起任何作用。
• $0 < \alpha_i < C$: 第 i 个训练点是支持向量，位于间隔上。对于此点，$\xi_i = 0$ 且 $t_i(w^T x_i + w_0) = 1$，因此它可用于计算 $w_0$。实践中，$w_0$ 是从所有支持向量计算并取平均值。
• $\alpha_i = C$: 第 i 个训练点要么位于间隔内部的正确一侧，要么位于超平面的错误一侧。

下图将帮助您理解上述概念

确定测试点的分类

任何测试点$x$的分类都可以使用以下表达式确定

$$
y(x) = \sum_i \alpha_i t_i x^T x_i + w_0
$$

$y(x)$ 的正值表示 $x\in+1$，负值表示 $x\in-1$。因此，测试点的预测类别是 $y(x)$ 的符号。

库恩-塔克（KKT）条件

上述约束优化问题满足库恩-塔克（KKT）条件，具体如下：
\begin{eqnarray}
\alpha_i &\geq& 0 \\
t_i y(x_i) -1 + \xi_i &\geq& 0 \\
\alpha_i(t_i y(x_i) -1 + \xi_i) &=& 0 \\
\mu_i \geq 0 \\
\xi_i \geq 0 \\
\mu_i\xi_i = 0
\end{eqnarray}

一个已解决的例子

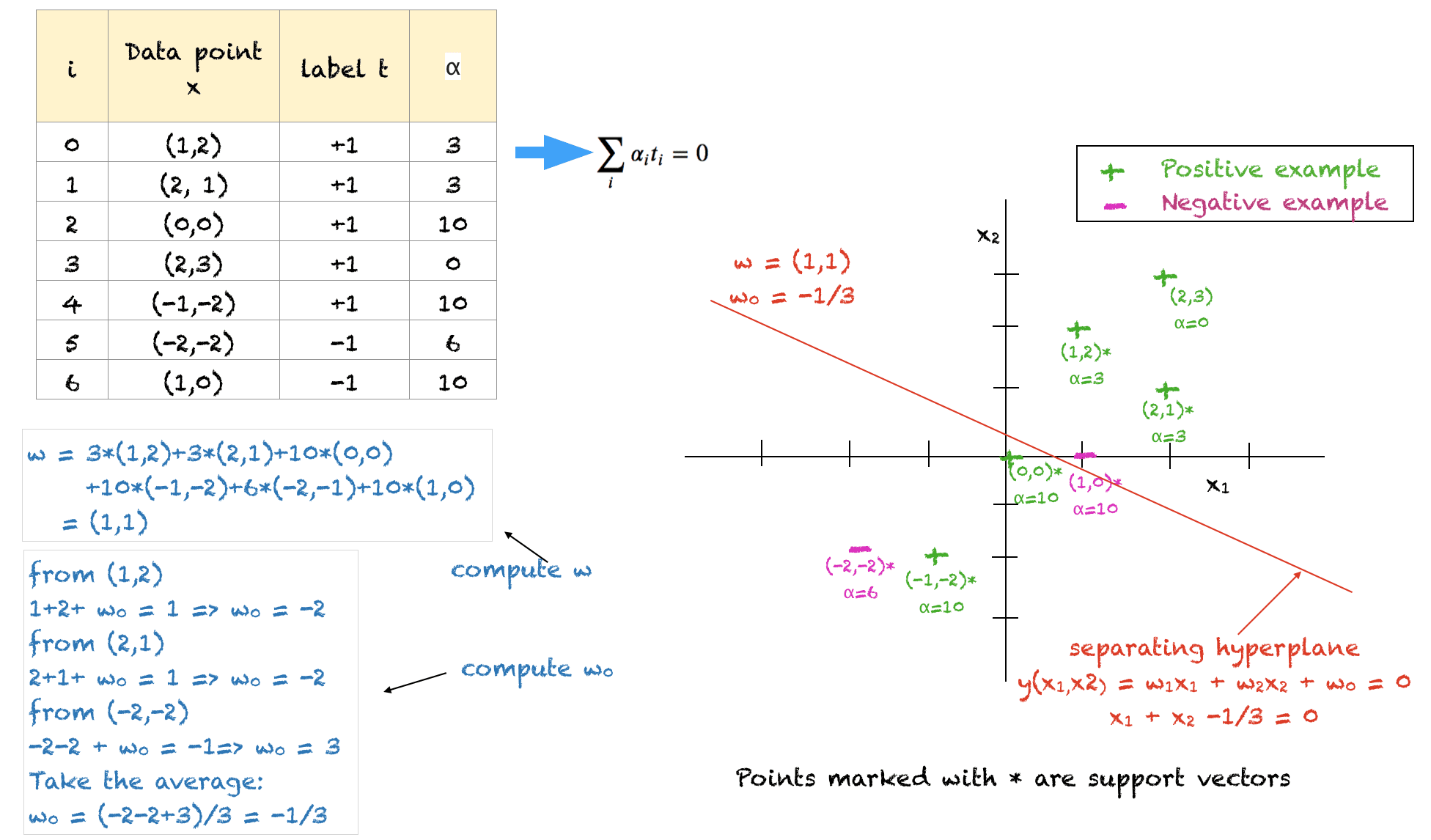
上面显示了一个用于二维训练点的已解决示例，以说明所有概念。关于此解决方案需要注意的几点是：

• 训练数据点及其相应的标签作为输入
• 用户定义的常数$C$设置为10
• 该解决方案满足所有约束，但它不是最优解
• 我们必须确保所有$\alpha$都介于0和C之间
• 所有负例的alpha之和应等于所有正例的alpha之和
• 点 (1,2)、(2,1) 和 (-2,-2) 位于超平面正确一侧的软间隔上。它们的值被任意设置为 3、3 和 6，以平衡问题并满足约束。
• $\alpha=C=10$ 的点要么位于间隔内部，要么位于超平面的错误一侧

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

• 克里斯托弗·M·毕肖普的《模式识别与机器学习》

文章

• 机器学习中的支持向量机
• 克里斯托弗·J·C·伯吉斯的《模式识别支持向量机教程》

总结

在本教程中，您学习了拉格朗日乘数法，用于在 SVM 分类器中寻找软间隔。

具体来说，你学到了：

• 如何针对不可分情况制定优化问题
• 如何使用拉格朗日乘数法找到超平面和软间隔
• 如何为非常简单的问题找到分离超平面的方程

您对本文讨论的 SVM 有任何疑问吗？请在下面的评论中提出您的问题，我将尽力回答。

掌握机器学习微积分！

通过微积分概念变得更聪明

...通过更好地理解微积分的符号和术语

在我的新电子书中探索如何实现
机器学习微积分

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
微分、梯度、拉格朗日乘子法、雅可比矩阵等等...

将恰到好处的微积分知识带到
您的机器学习项目

查看内容