Hessian矩阵属于一类包含二阶导数的数学结构。它们常用于机器学习和数据科学算法中，用于优化感兴趣的函数。
在本教程中，您将了解 Hessian 矩阵、它们对应的判别式以及它们的重要性。所有概念都将通过一个示例进行说明。
完成本教程后，您将了解：
- Hessian矩阵
- 通过 Hessian 矩阵计算的判别式
- 判别式包含什么信息
让我们开始吧。
Hessian矩阵入门指南。图片由Beenish Fatima拍摄，保留部分权利。
教程概述
本教程分为三个部分；它们是：
- 函数 Hessian 矩阵的定义及对应的判别式
- 计算 Hessian 矩阵和判别式的示例
- Hessian 和判别式告诉我们关于目标函数的哪些信息
先决条件
对于本教程，我们假设您已经了解
您可以通过点击上面给出的链接来复习这些概念。
什么是 Hessian 矩阵？
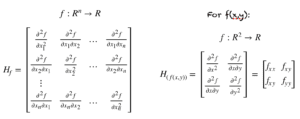
Hessian 矩阵是二阶偏导数组成的矩阵。假设我们有一个 n 个变量的函数 f，即
$$f: R^n \rightarrow R$$
f 的 Hessian 由左侧的矩阵表示。双变量函数的 Hessian 也显示在右侧。
n 个变量函数的 Hessian（左）。f(x,y) 的 Hessian（右）
我们在关于梯度向量的教程中已经知道，梯度是关于一阶偏导数的向量。类似地，Hessian 是由 f 定义域中所有变量对组成的一阶偏导数矩阵。
想开始学习机器学习微积分吗？
立即参加我为期7天的免费电子邮件速成课程（附示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
什么是判别式？
Hessian 的**行列式**也称为 f 的判别式。对于双变量函数 f(x, y)，它由下式给出
f(x, y) 的判别式
Hessian 矩阵和判别式的示例
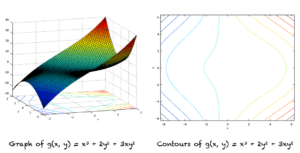
假设我们有以下函数
g(x, y) = x^3 + 2y^2 + 3xy^2
则 Hessian H_g 和判别式 D_g 分别由下式给出
g(x, y) = x^3 + 2y^2 + 3xy^2 的 Hessian 和判别式
让我们在不同的点上计算判别式
D_g(0, 0) = 0
D_g(1, 0) = 36 + 24 = 60
D_g(0, 1) = -36
D_g(-1, 0) = 12
Hessian 和判别式有什么意义？
Hessian 及其对应的判别式用于确定函数的局部极值点。评估它们有助于理解多变量函数。以下是对于判别式为 D(a, b) 的点 (a,b) 的一些重要规则：
- 如果 f_xx(a, b) > 0 且判别式 D(a,b) > 0，则函数 f 具有**局部最小值**。
- 如果 f_xx(a, b) < 0 且判别式 D(a,b) > 0，则函数 f 具有**局部最大值**。
- 如果 D(a, b) < 0，则函数 f 具有鞍点。
- 如果 D(a, b) = 0，我们无法得出任何结论，需要进行更多测试。
示例：g(x, y)
对于函数 g(x,y)
- 我们无法对点 (0, 0) 得出任何结论。
- f_xx(1, 0) = 6 > 0 且 D_g(1, 0) = 60 > 0，因此 (1, 0) 是一个局部最小值。
- 点 (0,1) 是一个鞍点，因为 D_g(0, 1) < 0
- f_xx(-1,0) = -6 < 0 且 D_g(-1, 0) = 12 > 0，因此 (-1, 0) 是一个局部最大值。
下图显示了函数 g(x, y) 的图形及其对应的等高线。
g(x,y) 的图形和 g(x,y) 的等高线
Hessian 矩阵在机器学习中为何重要？
Hessian 矩阵在许多涉及优化给定函数的机器学习算法中起着重要作用。虽然计算起来可能成本很高，但它包含了关于被优化函数的一些关键信息。它可以帮助确定函数的鞍点和局部极值。它广泛用于训练神经网络和深度学习架构。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 优化
- Hessian 矩阵的特征值
- Hessian 矩阵的逆与神经网络训练
如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。
进一步阅读
如果您想深入了解，本节提供了更多关于该主题的资源。
教程
资源
- 关于机器学习微积分书籍的额外资源
书籍
- 托马斯微积分，第 14 版，2017 年。（基于 George B. Thomas 的原创作品，由 Joel Hass、Christopher Heil、Maurice Weir 修订）
- 微积分，第三版，2017。（Gilbert Strang）
- 微积分，第 8 版，2015 年。（James Stewart）
总结
在本教程中，您了解了 Hessian 矩阵。具体来说，您学习了
- 海森矩阵
- 函数的判别式
你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。
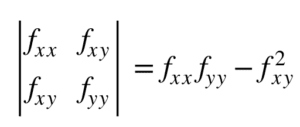
你好，Mehreen Saeed
我有一个建议，能否将应用与课程结合，使用 Python，并展示一些使用机器学习的实际问题，因为我们需要使用技术来实时解决实际问题。另一方面，CV也可以在其上发布，比如自定义对象跟踪检测，非常感谢！
好的，此类文章会跟进。对于本文，我们专注于在 Python 实现之前学习数学。始终最好先理解事物的工作原理，然后再进行实现部分 🙂
感谢您费心撰写这篇文章。
🙂
小提示：您关于判别式仅为正或负的规则仅适用于 2x2 矩阵。对于更高维度的矩阵，通用规则是 Hessian 必须是正定或负定才能确定极值。当然，对于对称的 2x2 矩阵，行列式为正可以保证两个特征值都为正；所以虽然您说这对 2x2 矩阵有效，但我认为它并不普遍适用。尽管如此，您说“评估它们有助于理解多变量函数”，这表明您所说的可以推广。
现在，可能是我弄错了，但如果是这样，请告诉我。
使用 S-Math studio 的分步解决方案可能更具启发性。
100% 特征值和 Hessian。
好帖子！谢谢！
通常在机器学习问题中，我们不知道显式函数 y =f(x1,…xn)。并且我们解决了它……它并没有给我们这种显式的输入-输出依赖关系……
所以，除了测试一个已知的函数，通过一个离散的数据集生成，然后通过一些遗传算法或类似方法来尝试识别数据集的最大值和最小值，我们可以在 Hessian 分量和判别式分析中直接检查……我不知道 Hessian 矩阵是如何用于机器学习算法的？
致敬
谢谢，Mehreen。您的解释非常出色！Python 代码示例会非常有帮助！
你好 Mehreen，
你能告诉我们如何找到多变量函数的 Hessian 矩阵吗？
比如 fx(theta1, theta2)=0 和 fy(theta1, theta2)=0。我知道如何为 fx 和 fy 获取 Jacobian 矩阵，但如何为两者都获取 Hessian 呢？
Hessian 矩阵用于标量值函数。如果您将 fx 和 fy 视为两个独立的函数，则可以分别获得它们的 Hessian。如果您将 [fx,fy] 视为一个向量（因此是一个向量值函数），您只能获得 Jacobian。
我不明白的是：为什么不能仅通过查看 fxx 和 fyy 来确定一个点是最大值、最小值还是鞍点？为什么需要计算 D = fxx + fyy – (fxy)^2？
看起来很容易看出，如果 fxx 和 fyy 都为负，则表示最大值；如果都为正，则表示最小值；如果一个为正一个为负，则表示鞍点。您能否举一个例子，其中 fxx 和 fyy 具有相同的符号，但曲面却是一个鞍点？
也许我没有理解 fxy 的几何解释（如果存在的话）？是否存在？
谢谢！
这是我找到的关于此主题的最佳文章。
你好 Ken…如果你已经有了一个曲面，你可以通过视觉检查来判断它似乎有一个最大值或最小值。方程在数学上证明了这一点。这很重要，因为其他代码无法像我们人类那样“视觉检查”曲线。所以，如果需要根据找到的最大值和/或最小值做出其他决定，就必须有数学依据。