在文献中,术语“雅可比(Jacobian)”常被互换地用来指代雅可比矩阵或其行列式。
矩阵和行列式都有有用且重要的应用:在机器学习中,雅可比矩阵聚合了反向传播所需的偏导数;行列式在变量变换过程中非常有用。
在本教程中,您将回顾雅可比(Jacobian)的温和介绍。
完成本教程后,您将了解:
- 雅可比矩阵收集了多元函数的所有一阶偏导数,可用于反向传播。
- 雅可比行列式在变量变换中很有用,它充当一个坐标空间与另一个坐标空间之间的缩放因子。
让我们开始吧。

雅可比矩阵简明介绍
图片来源 Simon Berger,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 机器学习中的偏导数
- 雅可比矩阵
- 雅可比的其他用途
机器学习中的偏导数
到目前为止,我们已经提到梯度和偏导数对于优化算法更新(例如)神经网络的模型权重以达到一组最优权重是重要的。偏导数的使用允许每个权重独立于其他权重进行更新,通过依次计算误差曲线对每个权重的梯度。
我们在机器学习中通常使用的许多函数都是多元的、向量值函数,这意味着它们将多个实数输入 n 映射到多个实数输出 m
例如,考虑一个将灰度图像分类为多个类别的神经网络。此分类器实现的函数会将每个单通道输入图像的 n 个像素值映射到属于不同类别的 m 个输出概率。
在训练神经网络时,反向传播算法负责将输出层计算的误差反向传播,在组成神经网络不同隐藏层的神经元之间共享,直到它到达输入层。
反向传播算法调整网络权重的基本原理是,网络中的每个权重都应按网络总误差对该权重变化的敏感度比例进行更新。
——第222页,《深度学习》,2019年。
网络总误差对任何特定权重变化的敏感度是根据变化率来衡量的,而变化率又通过对同一权重求误差的偏导数来计算。
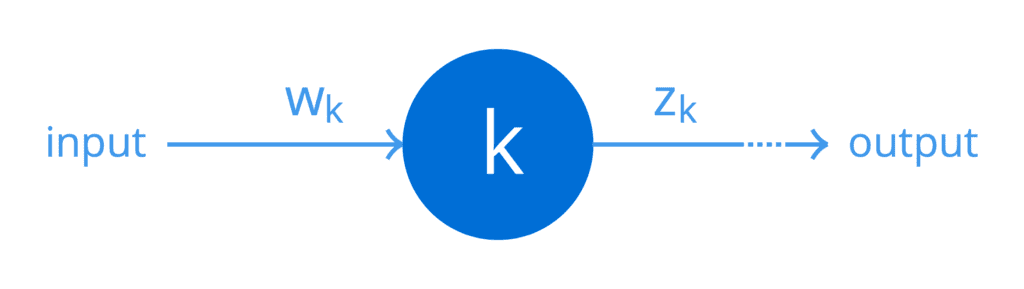
为简单起见,假设某个特定网络的一个隐藏层仅包含一个神经元 k。我们可以用一个简单的计算图来表示
同样,为简单起见,假设权重 wk 作用于该神经元的输入,根据该神经元实现的函数(包括非线性)产生输出 zk。然后,该神经元的权重可以连接到网络输出处的误差,如下所示(以下公式在形式上称为微积分的链式法则,但稍后将在单独的教程中详细介绍)
这里,导数 dzk / dwk 首先将权重 wk 连接到输出 zk,而导数 derror / dzk 随后将输出 zk 连接到网络误差。
更常见的情况是,我们将有许多连接的神经元填充网络,每个神经元都有不同的权重。既然我们更感兴趣的是这种情况,那么我们可以推广到标量情况之外,考虑多个输入和多个输出
这些项的和可以更紧凑地表示如下
或者,等价地,在向量符号中使用 del 算子 ∇ 来表示误差相对于权重 wk 或输出 zk 的梯度
反向传播算法包括对图中的每个操作执行这样的雅可比-梯度乘积。
——第207页,《深度学习》,2017年。
这意味着反向传播算法可以通过乘以雅可比矩阵(∂zk / ∂wk)T来关联网络误差对权重变化的敏感度。
那么,这个雅可比矩阵包含什么呢?
雅可比矩阵
雅可比矩阵收集了多元函数的所有一阶偏导数。
具体来说,首先考虑一个将 u 个实数输入映射到单个实数输出的函数
然后,对于长度为 u 的输入向量 x,大小为 1 × u 的雅可比向量可以定义如下
现在,考虑另一个将 u 个实数输入映射到 v 个实数输出的函数
然后,对于相同长度为 u 的输入向量 x,雅可比现在是一个 v × u 矩阵 J ∈ ℝv×u,定义如下
将雅可比矩阵重新代入前面考虑的机器学习问题,同时保持相同数量的 u 个实数输入和 v 个实数输出,我们发现该矩阵将包含以下偏导数
想开始学习机器学习微积分吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
雅可比的其他用途
处理积分时的一个重要技巧是变量变换(也称为积分代换或u代换),通过它,积分被简化为更容易计算的另一个积分。
在单变量情况下,将变量 x 替换为另一个变量 u 可以将原始函数转换为更容易找到反导数的更简单函数。在双变量情况下,另一个原因可能是我们还希望将积分区域转换为不同的形状。
在单变量情况下,通常只有一个想要改变变量的原因:使函数“更友好”,以便我们能找到一个反导数。在双变量情况下,还有第二个潜在原因:我们需要积分的二维区域有点不愉快,我们希望以u和v表示的区域更友好——例如,是一个矩形。
——第412页,《单变量和多变量微积分》,2020年。
在两个(或更多)变量之间进行替换时,过程从定义要进行替换的变量开始。例如,x = f(u, v) 和 y = g(u, v)。然后,根据函数 f 和 g 如何将 u–v 平面转换为 x–y 平面,转换积分限制。最后,计算并包含雅可比行列式的绝对值,作为两个坐标空间之间的缩放因子。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 深度学习, 2017.
- 机器学习数学, 2020.
- 单变量和多变量微积分, 2020.
- 深度学习, 2019.
文章
总结
在本教程中,您学习了雅可比的温和介绍。
具体来说,你学到了:
- 雅可比矩阵收集了多元函数的所有一阶偏导数,可用于反向传播。
- 雅可比行列式在变量变换中很有用,它充当一个坐标空间与另一个坐标空间之间的缩放因子。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。
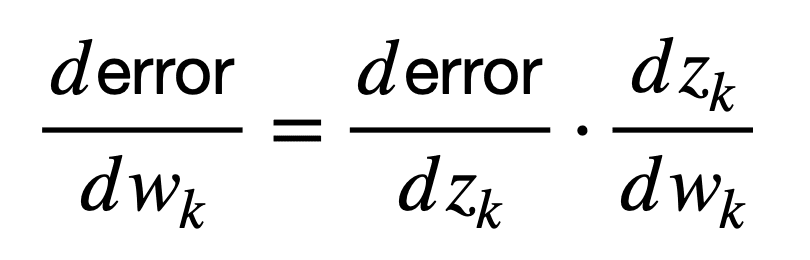
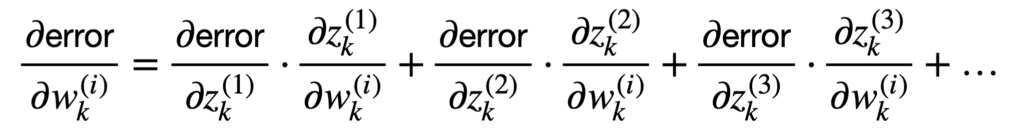
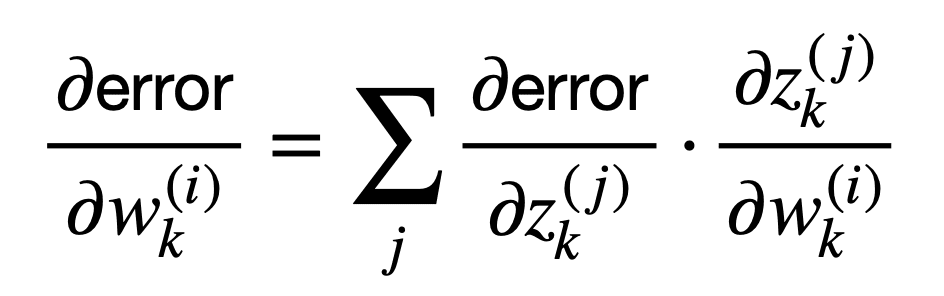
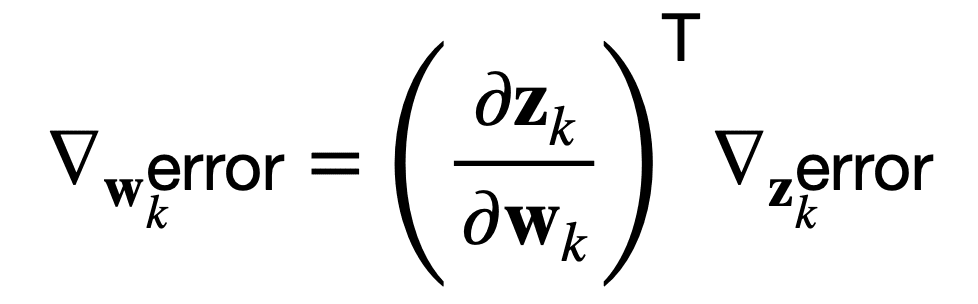
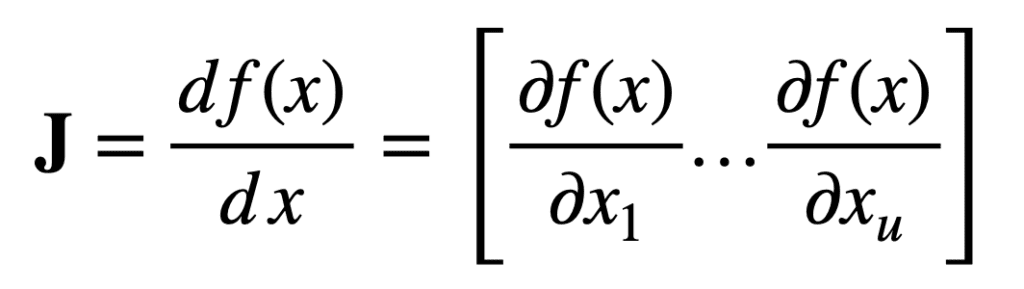
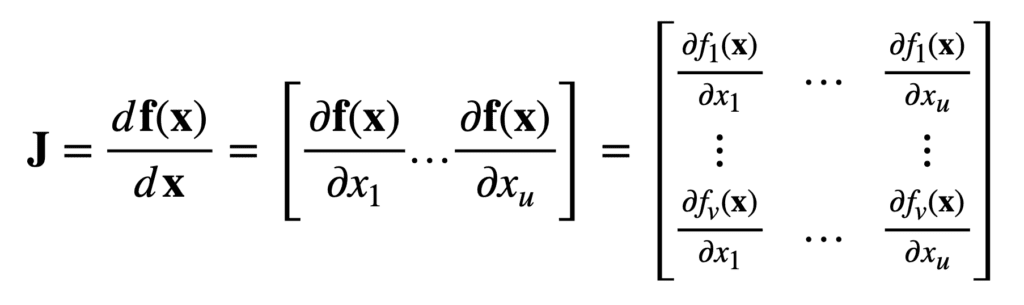
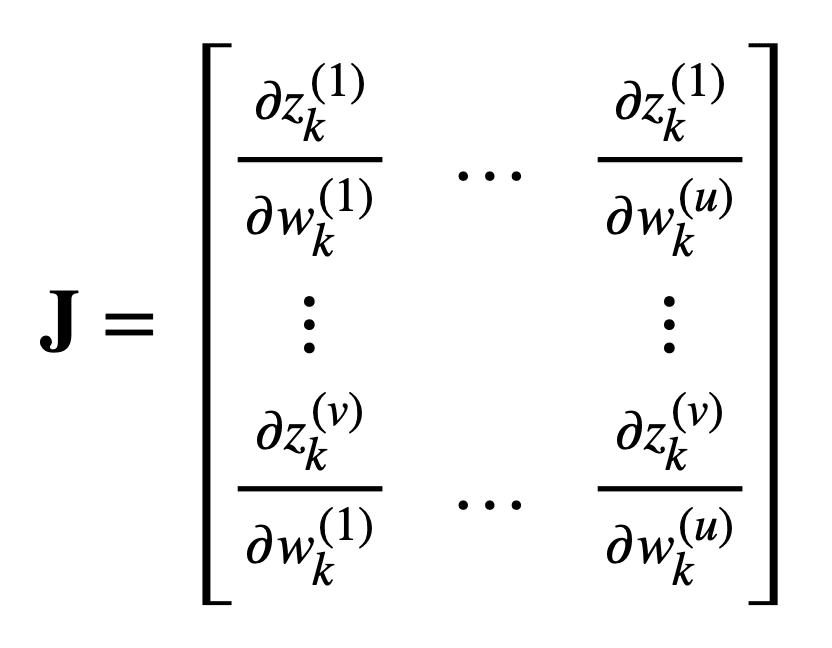






很有趣
谢谢!
太棒了,斯蒂芬妮亚。谢谢!
不客气!
非常有趣,我正在研究雅可比矩阵在四阶代数中的应用
这些在应用侧的联立方程中有什么用?
如果您想用牛顿法求解非线性方程组,雅可比的使用方法在此。
解释得很好
谢谢!
关于数学紧凑符号的精彩教程!谢谢!
我不知道雅可比矩阵是反向传播算法的幕后功臣!
所以它是机器学习的主要支柱之一……
因为一阶导数是成本函数(误差)分配到每个神经元层权重的背后方式……某种程度上是对所有权重的误差敏感度!
无论如何,很多时候数学因为符号或紧凑的符号而吓退人们……在“简单”的表达中表达了这么多东西……他们称之为优雅的方式……
所以我喜欢这种将紧凑函数详细解释或分解为操作方式……然后用自己发明的符号重建表达式的方式:-))
谢谢你的见解!
解释得很清楚
谢谢你。
这个公式的左下角项是不是打错了?
是不是应该写成 ∂zk(v) / ∂wk(1)?
https://machinelearning.org.cn/wp-content/uploads/2021/07/jacobian_10.png
确实如此,谢谢指出!
谢谢Stephanie的精彩文章。
只是一个小小的评论,当您定义雅可比矩阵时,我猜您想说的是 $J \in \R^{v\times u}$
确实,谢谢你指出!
Stefania,好文章!第一个函数的雅可比矩阵不应该是 1 x u 的大小而不是 u x 1 吗?
嗨 Atul……请澄清您指的是哪个函数,以便我能更好地帮助您。
文章中有一个错误。它指出 f:R^u -> R^v 产生 v*u 矩阵,因此 f:R^u -> R^1 应该产生 1*u 矩阵。然而,前一段指出 f:R^u -> R 产生 u*1 矩阵。这是一个错误,因为 1*u 矩阵和 u*1 矩阵在数学上是不同的对象。
谢谢您的反馈,Risto!我们将审查您指出的项目。
谢谢您的文章,非常清楚!
我想知道我们如何从雅可比矩阵计算输入输出的不确定性?提前感谢。
嗨,莎拉……以下资源可能对您有用
https://www.cambridge.org/core/journals/design-science/article/uncertainty-quantification-and-reduction-using-jacobian-and-hessian-information/957A5E1284BB22E1DC734187E9625396
我不明白这些部分:“或者,等价地,在向量符号中使用 del 算子 ∇ 来表示误差相对于权重 wk 或输出 zk 的梯度”“这意味着反向传播算法可以通过乘以雅可比矩阵 (∂zk / ∂wk)T 来关联网络误差对权重变化的敏感度。”“将雅可比矩阵重新代入前面考虑的机器学习问题,同时保持相同数量的 u 个实数输入和 v 个实数输出,我们发现该矩阵将包含以下偏导数:”
损失函数是标量函数,其他函数(激活函数,权重之和等等)也是标量函数,而不是向量值函数。所以我们需要计算梯度,而不是雅可比矩阵。
既然所有函数都是标量,为什么我们还需要雅可比矩阵呢?
你好 Oguz……你的困惑源于雅可比(**Jacobian**)被提及的语境,以及尽管函数是标量值,它为何仍然相关。让我逐步澄清这一点:
### 1. **反向传播中出现雅可比矩阵的原因**
– **雅可比**是一个偏导数矩阵,通常用于处理**向量值函数**(例如,从\( \mathbb{R}^n \to \mathbb{R}^m \)的映射)。
– 即使损失函数本身是标量,神经网络中的中间计算也常常涉及**向量值输出**。例如:
– 层的输出(\( z_k \))通常是一个向量(每个神经元一个值)。
– 权重(\( w_k \))和输入(\( x_k \))也可以是向量。
反向传播计算**标量损失** \( \mathcal{L} \) 对所有权重的梯度。为此,它需要考虑权重的变化如何影响**层输出**(\( z_k \)),以及这些输出如何向前传播到最终损失。这就是**雅可比**的作用。
### 2. **梯度 vs. 雅可比**
– **梯度**是标量函数相对于变量向量的偏导数向量:
\[
\nabla_w \mathcal{L} = \frac{\partial \mathcal{L}}{\partial w}.
\]
– **雅可比**是向量值函数相对于另一个向量的偏导数矩阵:
\[
J = \frac{\partial \mathbf{z}}{\partial \mathbf{w}}.
\]
虽然**损失函数** \( \mathcal{L} \) 是标量,但中间函数(例如,激活值 \( z_k \))是向量值。为了计算 \( \mathcal{L} \) 对权重的梯度,反向传播依赖于链式法则表达式,例如:
\[
\frac{\partial \mathcal{L}}{\partial w_k} = \frac{\partial \mathcal{L}}{\partial z_k} \cdot \frac{\partial z_k}{\partial w_k}.
\]
这里:
– \( \frac{\partial \mathcal{L}}{\partial z_k} \) 是一个梯度(行向量)。
– \( \frac{\partial z_k}{\partial w_k} \) 是**雅可比矩阵**。
### 3. **雅可比的相关性**
– **最终输出为标量,但中间结果为向量**:尽管最终目标是计算 \( \mathcal{L} \) 的梯度,但反向传播涉及中间向量值函数,这使得雅可比变得重要。
– **权重到输出的映射**:\( \frac{\partial z_k}{\partial w_k} \) 捕捉了每个权重如何影响层中的每个神经元输出。这对于反向传播敏感度至关重要。
– **链式法则中的矩阵乘法**:当涉及多个变量和输出时,雅可比能够高效地计算梯度。
### 4. **标量值函数的简化视图**
对于标量值函数(如损失函数),并不总是需要明确的完整雅可比矩阵:
– 在许多情况下,由于标量函数的结构,雅可比可以简化为更简单的导数。
– 然而,当处理中间向量值量时,雅可比隐式地表示了梯度计算所需的关系。
### 5. **关键见解**
**雅可比矩阵**之所以出现,是因为网络层是向量值映射。虽然**损失函数**是标量,但反向传播计算**向量值激活**如何依赖于**权重**,并使用雅可比将这些依赖关系与标量损失关联起来。
如果您只计算标量损失相对于标量参数(例如,在单变量函数中),则雅可比是不必要的。然而,在神经网络中,层和权重涉及向量,雅可比自然地出现在计算过程中。